第15章概率 基础巩固测试-【新教材】2020-2021学年苏教版(2019)高中数学必修第二册(Word含解析)
文档属性
| 名称 | 第15章概率 基础巩固测试-【新教材】2020-2021学年苏教版(2019)高中数学必修第二册(Word含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 476.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-15 22:28:38 | ||
图片预览



文档简介
苏教版第15章概率基础巩固测试卷
一、单选题
1.在一个袋子中放个白球,个红球,摇匀后随机摸出个球,与“摸出个白球个红球”互斥而不对立的事件是( )
A.至少摸出个白球 B.至少摸出个红球
C.摸出个白球 D.摸出个白球或摸出个红球
2.五一放假,甲、乙、丙去厦门旅游的概率分别是、、,假定三人的行动相互之间没有影响,那么这段时间内至少有1人去厦门旅游的概率为( )
A. B. C. D.
3.为了了解参加学校体育节的1200名学生的身高情况,从中抽取40名运动员进行测量.下列说法正确的是( )
A.总体是1200名学生
B.个体是每一名运动员
C.40名学生的身高是一个个体
D.样本容量是40
4.从2016年1月1日起,“全面二孩”政策在全国范围内实施,许多年轻夫妇都积极地响应国家号召,在六年内生育了二胎,因此在有两个孩子的每户家庭中,若按孩子的性别来进行分类,共会出现三类家庭,分别为:“两个男孩型”家庭,“一男一女孩型”家庭,“两个女孩型”家庭.市消费者协会为了解有两个孩子家庭的某些日常生活消费指数,从该市有两个孩子(假设每胎只生一个小孩,科学研究证明每胎生男生女机会均等)的家庭中随机地抽取户进行调查统计,则估计其中是“一男一女孩型”家庭的户数为( )
A. B. C. D.
5.从一群参加新年晚会的小孩中随机抽出k人,一人发一个礼物,让他们返回继续参加晚会,过了一会儿,再从中任取m人,发现其中有n个小孩曾发过礼物,估计参加新年晚会的小孩的人数为( )
A. B. C. D.
6.一个人打靶时连续射击两次,事件“两次都没中靶”的相互对立事件是( )
A.至多有一次中靶 B.至少有一次中靶 C.两次都中靶 D.只有一次中靶
7.某篮球运动员进行投球练习,连投了100次,恰好投进了90次.若用A表示“投进球”这一事件,则事件A发生的( )
A.概率为0.9 B.频率为90 C.频率为0.9 D.以上说法都不对
8.一商店有奖促销活动中仅有一等奖、二等奖、鼓励奖三个奖项,其中中一等奖的概率为0.1,中二等奖的概率为0.32,中鼓励奖的概率为0.42,则不中奖的概率为( )
A.0.16 B.0.12 C.0.18 D.0.58
二、多选题
9.袋中装有形状完全相同的个白球和个黑球,从中一次摸出个球,下列事件是互斥事件的是( )
A.摸出三个白球事件和摸出三个黑球事件
B.恰好有一黑球事件和都是黑球事件
C.至少一个黑球事件和至多一个白球事件
D.至少一个黑球事件和全是白球事件
10.下列事件中,是随机事件的是( )
A.年月日,北京市不下雨
B.在标准大气压下,水在时结冰
C.从标有,,,的张号签中任取一张,恰为号签
D.若,则
11.若,为互斥事件,,分别表示事件,发生的概率,则下列说法正确的是( )
A. B.
C. D.
12.某院校教师情况如下表所示
类别 老年 中年 青年
年度 男 女 男 女 男 女
2016 120 60 240 120 100 40
2017 210 40 320 200 200 120
2018 300 150 400 270 320 280
关于2016年、2017年、2018年这3年该院校的教师情况,下面说法正确的是( )
A.2017年男教师最多
B.该校教师最多的是2018年
C.2017年中年男教师比2016年多80人
D.2016年到2018年,该校青年年龄段的男教师人数增长率为220%
三、填空题
13.已知事件A,B满足,若P(A)=0.3,则P(B)=_____.
14.甲?乙两名同学进行篮球投篮练习,甲同学一次投篮命中的概率为,乙同学一次投篮命中的概率为,假设两人投篮命中与否互不影响,则甲?乙两人各投篮一次,至少有一人命中的概率是___________.
15.某商店的有奖促销活动中仅有一等奖?二等奖?鼓励奖三个奖项,其中中一等奖的概率为0.05,中二等奖的概率为0.16,中鼓励奖的概率为0.40,则不中奖的概率为________.
16.下列说法:①随机事件A的概率是频率值的稳定值,频率是概率的近似值;
②抛掷骰子100次,得点数是1的结果是18次,则出现1点的频率是;
③随机事件A的概率趋近于0,即P(A)→0,则A是不可能事件.
④任意事件A发生的概率总满足0<P(A)<1
其中正确的有________.
四、解答题
17.某商场有奖销售中,购满100元商品得1张奖券,多购多得,1 000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.记1张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C,求:
(1)1张奖券的中奖概率;
(2)1张奖券不中特等奖且不中一等奖的概率.
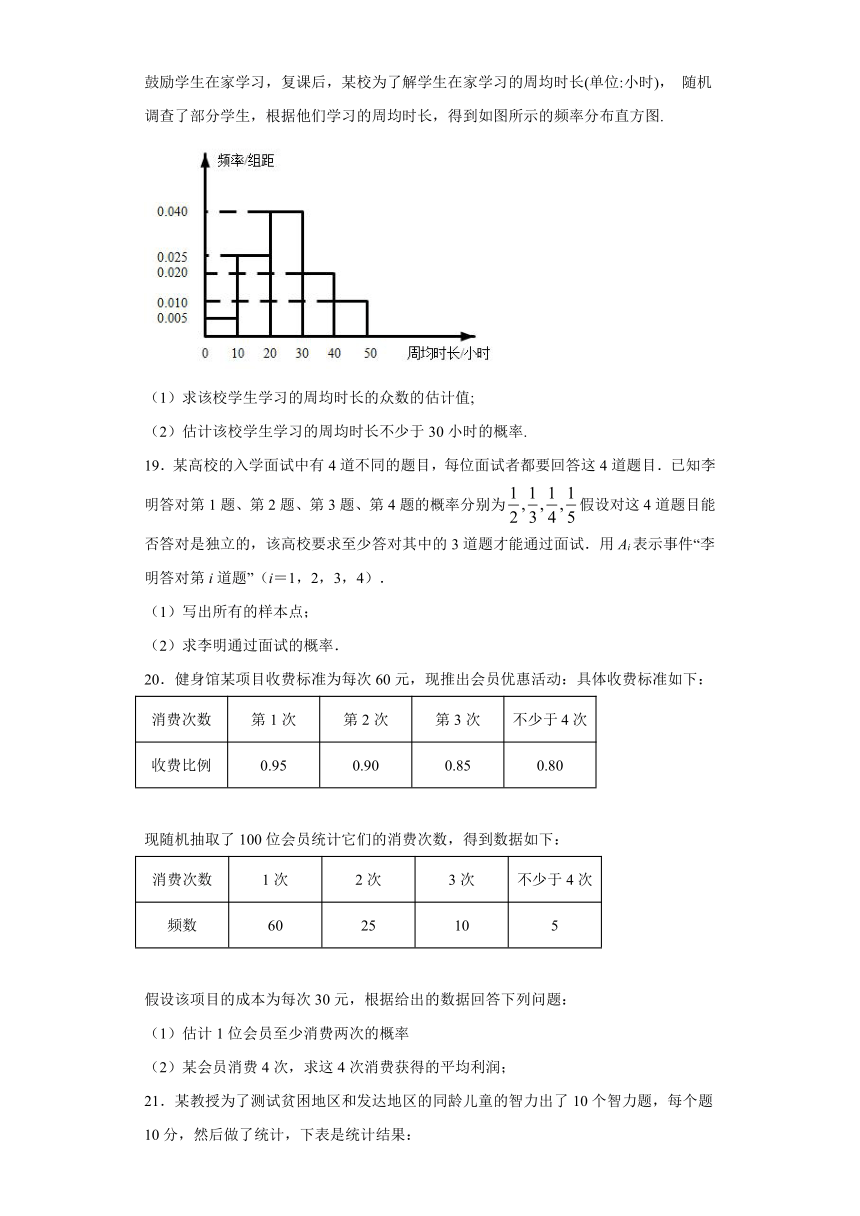
18.2020年春季,受疫情的影响,学校推迟了开学时间.上级部门倡导“停课不停学”,鼓励学生在家学习,复课后,某校为了解学生在家学习的周均时长(单位:小时), 随机调查了部分学生,根据他们学习的周均时长,得到如图所示的频率分布直方图.
(1)求该校学生学习的周均时长的众数的估计值;
(2)估计该校学生学习的周均时长不少于30小时的概率.
19.某高校的入学面试中有4道不同的题目,每位面试者都要回答这4道题目.已知李明答对第1题、第2题、第3题、第4题的概率分别为假设对这4道题目能否答对是独立的,该高校要求至少答对其中的3道题才能通过面试.用Ai表示事件“李明答对第i道题”(i=1,2,3,4).
(1)写出所有的样本点;
(2)求李明通过面试的概率.
20.健身馆某项目收费标准为每次60元,现推出会员优惠活动:具体收费标准如下:
消费次数 第1次 第2次 第3次 不少于4次
收费比例 0.95 0.90 0.85 0.80
现随机抽取了100位会员统计它们的消费次数,得到数据如下:
消费次数 1次 2次 3次 不少于4次
频数 60 25 10 5
假设该项目的成本为每次30元,根据给出的数据回答下列问题:
(1)估计1位会员至少消费两次的概率
(2)某会员消费4次,求这4次消费获得的平均利润;
21.某教授为了测试贫困地区和发达地区的同龄儿童的智力出了10个智力题,每个题10分,然后做了统计,下表是统计结果:
贫困地区
参加测试的人数 30 50 100 200 500 800
得60分以上的人数 16 27 52 104 256 402
得60分以上的频率
发达地区
参加测试的人数 30 50 100 200 500 800
得60分以上的人数 17 29 56 111 276 440
得60分以上的频率
(1)利用计算器计算两地区参加测试的儿童中得60分以上的频率(结果精确到0.001);
(2)求两个地区参加测试的儿童得60分以上的概率.
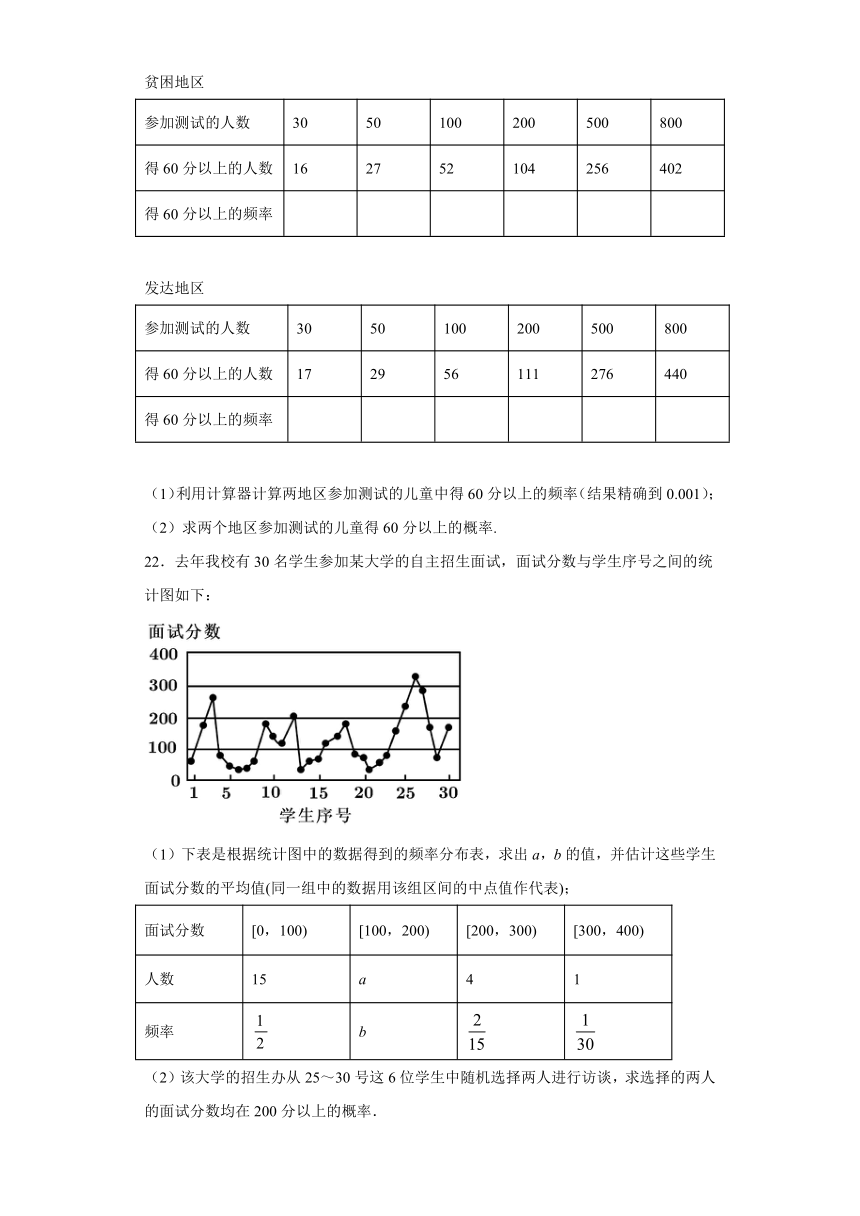
22.去年我校有30名学生参加某大学的自主招生面试,面试分数与学生序号之间的统计图如下:
(1)下表是根据统计图中的数据得到的频率分布表,求出a,b的值,并估计这些学生面试分数的平均值(同一组中的数据用该组区间的中点值作代表);
面试分数 [0,100) [100,200) [200,300) [300,400)
人数 15 a 4 1
频率
b
(2)该大学的招生办从25~30号这6位学生中随机选择两人进行访谈,求选择的两人的面试分数均在200分以上的概率.
参考答案
1.C
【分析】
根据互斥事件,对立事件的概念判断可得选项.
【详解】
对于A,至少摸出个白球与摸出个白球个红球不是互斥事件;
对于B,至少摸出个红球与摸出个白球个红球不是互斥事件;
对于C,摸出个白球与摸出个白球个红球是互斥而不对立事件;
对于D,摸出个白球或摸出个红球与摸出个白球个红球是互斥也是对立事件.
故选:C.
2.B
【分析】
由对立事件为:三人都不去厦门旅游,求,应用求概率即可.
【详解】
记事件至少有1人去厦门旅游,其对立事件为:三人都不去厦门旅游,
由独立事件的概率公式可得,
由对立事件的概率公式可得,
故选:B.
3.D
【分析】
根据题意可得出总体、个体、样本和样本容量.
【详解】
根据统计的相关概念并结合题意可得,总体是1200名学生的身高,个体是每一名运动员的身高,样本是抽取的40名学生的身高,样本容量是40,故ABC错误,D正确.
故选:D.
4.C
【分析】
根据题意把二胎的所有种类数枚举出来,找出其中“一男一女孩型”所占比例,即可求出抽取的600户中有多少这种类型家庭.
【详解】
因每胎生男女概率相等,则所有的两孩种类有,①第一胎男孩,第二胎男孩;②第一胎男孩,第二胎女孩;③第一胎女孩,第二胎男孩;④第一胎女孩,第二胎女孩;
故“一男一女孩型”所占概率为,则600户中有“一男一女孩型”.
故选:C.
5.C
【分析】
用样本频率估计总体频率,计算即可得.
【详解】
设总人数为,则,.
故选:C.
6.B
【分析】
直接根据对立事件的定义,可得事件“至少有一次中靶”的对立事件,从而得出结论.
【详解】
解:根据对立事件的定义可得,
事件“两次都没中靶”的对立事件是:至少有一次中靶,
故选:.
7.C
【分析】
根据频率计算公式,即可求得答案.
【详解】
投球一次即进行一次试验,投球100次,投进90次,
即事件A发生的频数为90,
所以事件A发生的频率为.
故选:C
8.A
【分析】
从1中减去中一等奖、二等奖、鼓励奖的概率,所得即为不中奖的概率.
【详解】
由于奖项一等奖、二等奖、鼓励奖和不中奖四个事件是相互独立,且构成事件为必然事件,
∴不中奖的概率为:,
故选:A.
【点睛】
本题考查互斥事件的概率计算,属简单题.
9.ABD
【分析】
根据互斥事件的定义可判断各选项的正误,从而可得正确的选项.
【详解】
对于A,摸出三个白球事件和摸出三个黑球事件不可能同时发生,故它们为互斥事件,故A正确.
对于B,恰好有一黑球事件和都是黑球事件不可能同时发生,故它们为互斥事件,故B正确.
对于C,比如三个球中两个黑球和1个白球,则至少一个黑球事件和至多一个白球事件可同时发生,故C错误.
对于D,至少一个黑球事件和全是白球事件也不可能同时发生,故D正确.
故选:ABD.
10.AC
【分析】
根据事件的概念进行判断,在某次实验中可能发生也可能不发生的事件成为随机事件.
【详解】
A选项与C选项为随机事件,B为不可能事件,D为必然事件.
故选:AC.
11.BD
【分析】
根据互斥事件的概念即可求得.
【详解】
解:互斥事件不可能同时发生,且互斥不一定对立,所以BD正确.
故选:BD.
12.BCD
【分析】
根据表格的信息进行数据分析,统计各年男教师人数,教师人数即可得答案;
【详解】
对A,2018年男教师最多1020,故A错误;
对B,2018年教师有1190最多,故B正确;
对C,2017年中年男教师320,2016年中年男教师240,故C正确;
对D,该校青年年龄段的男教师人数增长率为,故D正确;
故选:BCD.
【点睛】
本题考查统计的应用,考查数据处理能力,属于基础题.
13.0.7
【分析】
由题设理解A,B为对立事件,应用对立事件的概率公式求概率即可.
【详解】
由,知:事件A,B为对立事件,
∴.
故答案为:0.7.
14.
【分析】
考虑两个人都不命中的概率,从而可求至少有一个人命中的概率.
【详解】
两个都不命中的概率为,
故至少有一人命中的概率是,
故答案为:.
15.0.39
【分析】
利用互斥事件和对立事件的概率公式即可求解该题.
【详解】
中奖可分为三个互斥事件:一等奖、二等奖和鼓励奖,
故中奖的概率为:,
中奖与不中奖互为对立事件,
故不中奖的概率为:.
故答案为:.
16.①②
【分析】
根据频率和概率的定义和性质依次判断即可.
【详解】
对①,根据频率和概率的定义可得①正确;
对②,由题可得出现1点的频率是,故②正确;
对③,不可能事件的概率等于0,故③错误;
对④,任意事件A发生的概率总满足,故④错误.
故答案为:①②.
17.(1);(2).
【分析】
(1)1张奖券的中奖包括三种情况:中特等奖、一等奖、二等奖,由互斥事件的概率加法公式可求;
(2)利用对立事件可求.
【详解】
(1)设“1张奖券中奖”为事件M,则M=A∪B∪C,依题意,P(A)=,P(B)=,P(C)=,因为A,B,C两两互斥,
所以P(M)=P(A∪B∪C)=P(A)+P(B)+P(C)
==,
故1张奖券的中奖概率为.
(2)设“1张奖券不中特等奖且不中一等奖”为事件N,则事件N与“1张奖券中特等奖或中一等奖”为对立事件,所以P(N)=1-P(A∪B)=1-=.
故1张奖券不中特等奖且不中一等奖的概率为.
18.(1)25小时;(2)0.3.
【分析】
(1)根据直方图,频率最大的区间中点横坐标为众数即可求众数;(2)由学习的周均时长不少于30小时的区间有、,它们的频率之和,即为该校学生学习的周均时长不少于30小时的概率.
【详解】
(1)根据直方图知:频率最大的区间中点横坐标即为众数,
∴由频率最大区间为,则众数为;
(2)由图知:不少于30小时的区间有、,
∴该校学生学习的周均时长不少于30小时的概率.
【点睛】
本题考查了根据直方图求众数、概率,应用了众数的概念、频率法求概率,属于简单题.
19.(1) ;(2)
【分析】
(1)由题意知李明通过面试的样本点有:;
(2)由这4道题目能否答对是独立的,且李明答对第1题、第2题、第3题、第4题的概率分别为,即可求得李明通过面试的概率
【详解】
(1) 李明能通过面试的样本空间中样本点:
(2)由(1)知,李明通过面试的概率
,
又这4道题目能否答对是独立的,且李明答对第1题、第2题、第3题、第4题的概率分别为
∴,,
,,,
即.
【点睛】
本题考查了概率的概念及独立事件的概念计算,由题意任意答对3个及以上的题可通过面试即可写出通过面试的所有样本点,根据基本事件的独立性,利用独立事件的乘法概率公式求样本点概率,进而求得通过面试的概率
20.(1);(2).
【分析】
(1)根据消费次数表,利用频率估计概率;
(2)分别求出4次消费的利润,再求其平均值即可.
【详解】
(1)根据消费次数表,估计1位会员至少消费两次的概率;
(2)第1次消费利润;
第2次消费利润;
第3次消费利润;
第4次消费利润;
这4次消费获得的平均利润:.
【点睛】
本题考查利用频率估计概率,考查平均值的计算,属于简单题.
21.(1)见解析(2)贫困地区和发达地区参加测试的儿童得60分以上的概率分别为0.5和0.55.
【分析】
(1)根据所给表格,依次计算各组对应的频率值即可.
(2)随着测试人数的上升,可知频率值趋近于某个值,即为概率值.
【详解】
(1)根据频率计算公式,可得如下表所示:
贫困地区
参加测试的人数 30 50 100 200 500 800
得60分以上的人数 16 27 52 104 256 402
得60分以上的频率 0.533 0.540 0.520 0.520 0.512 0.503
发达地区
参加测试的人数 30 50 100 200 500 800
得60分以上的人数 17 29 56 111 276 440
得60分以上的频率 0.567 0.580 0.560 0.555 0.552 0.550
(2)随着测试人数的增加,两个地区参加测试的儿童得60分以上的频率逐渐趋近于0.5和0.55.
故贫困地区和发达地区参加测试的儿童得60分以上的概率分别为0.5和0.55.
【点睛】
本题考查了具体问题中频率的求法,频率与概率的关系,属于基础题.
22.(1)a=10,b=;面试分数的平均值为120分;(2).
【分析】
(1)由已知及频率分布表即可求参数,进而根据所得表格数据求平均值即可.
(2)列举出25~30号学生的所有可能的两人组合,根据折线图有25,26,27这三个号的学生面试分数均在200分以上,即可求概率.
【详解】
(1)面试分数在[100,200)内的学生共有30-15-4-1=10(名),故a=10,b==,
估计这些学生面试分数的平均值为50×+150×+250×+350×=120(分).
(2)从25~30号学生中任选两人的选择方法有(25,26),(25,27),(25,28),(25,29),(25,30),(26,27),(26,28),(26,29),(26,30),(27,28),(27,29),(27,30),(28,29),(28,30),(29,30)共15种,而由折线图知:25号,26号,27号学生的面试分数均在200分以上,
∴选择的两人的面试分数均在200分以上的选择方法有(25,26),(25,27),(26,27)共3种,故选择的两人的面试分数均在200分以上的概率为,即.
一、单选题
1.在一个袋子中放个白球,个红球,摇匀后随机摸出个球,与“摸出个白球个红球”互斥而不对立的事件是( )
A.至少摸出个白球 B.至少摸出个红球
C.摸出个白球 D.摸出个白球或摸出个红球
2.五一放假,甲、乙、丙去厦门旅游的概率分别是、、,假定三人的行动相互之间没有影响,那么这段时间内至少有1人去厦门旅游的概率为( )
A. B. C. D.
3.为了了解参加学校体育节的1200名学生的身高情况,从中抽取40名运动员进行测量.下列说法正确的是( )
A.总体是1200名学生
B.个体是每一名运动员
C.40名学生的身高是一个个体
D.样本容量是40
4.从2016年1月1日起,“全面二孩”政策在全国范围内实施,许多年轻夫妇都积极地响应国家号召,在六年内生育了二胎,因此在有两个孩子的每户家庭中,若按孩子的性别来进行分类,共会出现三类家庭,分别为:“两个男孩型”家庭,“一男一女孩型”家庭,“两个女孩型”家庭.市消费者协会为了解有两个孩子家庭的某些日常生活消费指数,从该市有两个孩子(假设每胎只生一个小孩,科学研究证明每胎生男生女机会均等)的家庭中随机地抽取户进行调查统计,则估计其中是“一男一女孩型”家庭的户数为( )
A. B. C. D.
5.从一群参加新年晚会的小孩中随机抽出k人,一人发一个礼物,让他们返回继续参加晚会,过了一会儿,再从中任取m人,发现其中有n个小孩曾发过礼物,估计参加新年晚会的小孩的人数为( )
A. B. C. D.
6.一个人打靶时连续射击两次,事件“两次都没中靶”的相互对立事件是( )
A.至多有一次中靶 B.至少有一次中靶 C.两次都中靶 D.只有一次中靶
7.某篮球运动员进行投球练习,连投了100次,恰好投进了90次.若用A表示“投进球”这一事件,则事件A发生的( )
A.概率为0.9 B.频率为90 C.频率为0.9 D.以上说法都不对
8.一商店有奖促销活动中仅有一等奖、二等奖、鼓励奖三个奖项,其中中一等奖的概率为0.1,中二等奖的概率为0.32,中鼓励奖的概率为0.42,则不中奖的概率为( )
A.0.16 B.0.12 C.0.18 D.0.58
二、多选题
9.袋中装有形状完全相同的个白球和个黑球,从中一次摸出个球,下列事件是互斥事件的是( )
A.摸出三个白球事件和摸出三个黑球事件
B.恰好有一黑球事件和都是黑球事件
C.至少一个黑球事件和至多一个白球事件
D.至少一个黑球事件和全是白球事件
10.下列事件中,是随机事件的是( )
A.年月日,北京市不下雨
B.在标准大气压下,水在时结冰
C.从标有,,,的张号签中任取一张,恰为号签
D.若,则
11.若,为互斥事件,,分别表示事件,发生的概率,则下列说法正确的是( )
A. B.
C. D.
12.某院校教师情况如下表所示
类别 老年 中年 青年
年度 男 女 男 女 男 女
2016 120 60 240 120 100 40
2017 210 40 320 200 200 120
2018 300 150 400 270 320 280
关于2016年、2017年、2018年这3年该院校的教师情况,下面说法正确的是( )
A.2017年男教师最多
B.该校教师最多的是2018年
C.2017年中年男教师比2016年多80人
D.2016年到2018年,该校青年年龄段的男教师人数增长率为220%
三、填空题
13.已知事件A,B满足,若P(A)=0.3,则P(B)=_____.
14.甲?乙两名同学进行篮球投篮练习,甲同学一次投篮命中的概率为,乙同学一次投篮命中的概率为,假设两人投篮命中与否互不影响,则甲?乙两人各投篮一次,至少有一人命中的概率是___________.
15.某商店的有奖促销活动中仅有一等奖?二等奖?鼓励奖三个奖项,其中中一等奖的概率为0.05,中二等奖的概率为0.16,中鼓励奖的概率为0.40,则不中奖的概率为________.
16.下列说法:①随机事件A的概率是频率值的稳定值,频率是概率的近似值;
②抛掷骰子100次,得点数是1的结果是18次,则出现1点的频率是;
③随机事件A的概率趋近于0,即P(A)→0,则A是不可能事件.
④任意事件A发生的概率总满足0<P(A)<1
其中正确的有________.
四、解答题
17.某商场有奖销售中,购满100元商品得1张奖券,多购多得,1 000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.记1张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C,求:
(1)1张奖券的中奖概率;
(2)1张奖券不中特等奖且不中一等奖的概率.
18.2020年春季,受疫情的影响,学校推迟了开学时间.上级部门倡导“停课不停学”,鼓励学生在家学习,复课后,某校为了解学生在家学习的周均时长(单位:小时), 随机调查了部分学生,根据他们学习的周均时长,得到如图所示的频率分布直方图.
(1)求该校学生学习的周均时长的众数的估计值;
(2)估计该校学生学习的周均时长不少于30小时的概率.
19.某高校的入学面试中有4道不同的题目,每位面试者都要回答这4道题目.已知李明答对第1题、第2题、第3题、第4题的概率分别为假设对这4道题目能否答对是独立的,该高校要求至少答对其中的3道题才能通过面试.用Ai表示事件“李明答对第i道题”(i=1,2,3,4).
(1)写出所有的样本点;
(2)求李明通过面试的概率.
20.健身馆某项目收费标准为每次60元,现推出会员优惠活动:具体收费标准如下:
消费次数 第1次 第2次 第3次 不少于4次
收费比例 0.95 0.90 0.85 0.80
现随机抽取了100位会员统计它们的消费次数,得到数据如下:
消费次数 1次 2次 3次 不少于4次
频数 60 25 10 5
假设该项目的成本为每次30元,根据给出的数据回答下列问题:
(1)估计1位会员至少消费两次的概率
(2)某会员消费4次,求这4次消费获得的平均利润;
21.某教授为了测试贫困地区和发达地区的同龄儿童的智力出了10个智力题,每个题10分,然后做了统计,下表是统计结果:
贫困地区
参加测试的人数 30 50 100 200 500 800
得60分以上的人数 16 27 52 104 256 402
得60分以上的频率
发达地区
参加测试的人数 30 50 100 200 500 800
得60分以上的人数 17 29 56 111 276 440
得60分以上的频率
(1)利用计算器计算两地区参加测试的儿童中得60分以上的频率(结果精确到0.001);
(2)求两个地区参加测试的儿童得60分以上的概率.
22.去年我校有30名学生参加某大学的自主招生面试,面试分数与学生序号之间的统计图如下:
(1)下表是根据统计图中的数据得到的频率分布表,求出a,b的值,并估计这些学生面试分数的平均值(同一组中的数据用该组区间的中点值作代表);
面试分数 [0,100) [100,200) [200,300) [300,400)
人数 15 a 4 1
频率
b
(2)该大学的招生办从25~30号这6位学生中随机选择两人进行访谈,求选择的两人的面试分数均在200分以上的概率.
参考答案
1.C
【分析】
根据互斥事件,对立事件的概念判断可得选项.
【详解】
对于A,至少摸出个白球与摸出个白球个红球不是互斥事件;
对于B,至少摸出个红球与摸出个白球个红球不是互斥事件;
对于C,摸出个白球与摸出个白球个红球是互斥而不对立事件;
对于D,摸出个白球或摸出个红球与摸出个白球个红球是互斥也是对立事件.
故选:C.
2.B
【分析】
由对立事件为:三人都不去厦门旅游,求,应用求概率即可.
【详解】
记事件至少有1人去厦门旅游,其对立事件为:三人都不去厦门旅游,
由独立事件的概率公式可得,
由对立事件的概率公式可得,
故选:B.
3.D
【分析】
根据题意可得出总体、个体、样本和样本容量.
【详解】
根据统计的相关概念并结合题意可得,总体是1200名学生的身高,个体是每一名运动员的身高,样本是抽取的40名学生的身高,样本容量是40,故ABC错误,D正确.
故选:D.
4.C
【分析】
根据题意把二胎的所有种类数枚举出来,找出其中“一男一女孩型”所占比例,即可求出抽取的600户中有多少这种类型家庭.
【详解】
因每胎生男女概率相等,则所有的两孩种类有,①第一胎男孩,第二胎男孩;②第一胎男孩,第二胎女孩;③第一胎女孩,第二胎男孩;④第一胎女孩,第二胎女孩;
故“一男一女孩型”所占概率为,则600户中有“一男一女孩型”.
故选:C.
5.C
【分析】
用样本频率估计总体频率,计算即可得.
【详解】
设总人数为,则,.
故选:C.
6.B
【分析】
直接根据对立事件的定义,可得事件“至少有一次中靶”的对立事件,从而得出结论.
【详解】
解:根据对立事件的定义可得,
事件“两次都没中靶”的对立事件是:至少有一次中靶,
故选:.
7.C
【分析】
根据频率计算公式,即可求得答案.
【详解】
投球一次即进行一次试验,投球100次,投进90次,
即事件A发生的频数为90,
所以事件A发生的频率为.
故选:C
8.A
【分析】
从1中减去中一等奖、二等奖、鼓励奖的概率,所得即为不中奖的概率.
【详解】
由于奖项一等奖、二等奖、鼓励奖和不中奖四个事件是相互独立,且构成事件为必然事件,
∴不中奖的概率为:,
故选:A.
【点睛】
本题考查互斥事件的概率计算,属简单题.
9.ABD
【分析】
根据互斥事件的定义可判断各选项的正误,从而可得正确的选项.
【详解】
对于A,摸出三个白球事件和摸出三个黑球事件不可能同时发生,故它们为互斥事件,故A正确.
对于B,恰好有一黑球事件和都是黑球事件不可能同时发生,故它们为互斥事件,故B正确.
对于C,比如三个球中两个黑球和1个白球,则至少一个黑球事件和至多一个白球事件可同时发生,故C错误.
对于D,至少一个黑球事件和全是白球事件也不可能同时发生,故D正确.
故选:ABD.
10.AC
【分析】
根据事件的概念进行判断,在某次实验中可能发生也可能不发生的事件成为随机事件.
【详解】
A选项与C选项为随机事件,B为不可能事件,D为必然事件.
故选:AC.
11.BD
【分析】
根据互斥事件的概念即可求得.
【详解】
解:互斥事件不可能同时发生,且互斥不一定对立,所以BD正确.
故选:BD.
12.BCD
【分析】
根据表格的信息进行数据分析,统计各年男教师人数,教师人数即可得答案;
【详解】
对A,2018年男教师最多1020,故A错误;
对B,2018年教师有1190最多,故B正确;
对C,2017年中年男教师320,2016年中年男教师240,故C正确;
对D,该校青年年龄段的男教师人数增长率为,故D正确;
故选:BCD.
【点睛】
本题考查统计的应用,考查数据处理能力,属于基础题.
13.0.7
【分析】
由题设理解A,B为对立事件,应用对立事件的概率公式求概率即可.
【详解】
由,知:事件A,B为对立事件,
∴.
故答案为:0.7.
14.
【分析】
考虑两个人都不命中的概率,从而可求至少有一个人命中的概率.
【详解】
两个都不命中的概率为,
故至少有一人命中的概率是,
故答案为:.
15.0.39
【分析】
利用互斥事件和对立事件的概率公式即可求解该题.
【详解】
中奖可分为三个互斥事件:一等奖、二等奖和鼓励奖,
故中奖的概率为:,
中奖与不中奖互为对立事件,
故不中奖的概率为:.
故答案为:.
16.①②
【分析】
根据频率和概率的定义和性质依次判断即可.
【详解】
对①,根据频率和概率的定义可得①正确;
对②,由题可得出现1点的频率是,故②正确;
对③,不可能事件的概率等于0,故③错误;
对④,任意事件A发生的概率总满足,故④错误.
故答案为:①②.
17.(1);(2).
【分析】
(1)1张奖券的中奖包括三种情况:中特等奖、一等奖、二等奖,由互斥事件的概率加法公式可求;
(2)利用对立事件可求.
【详解】
(1)设“1张奖券中奖”为事件M,则M=A∪B∪C,依题意,P(A)=,P(B)=,P(C)=,因为A,B,C两两互斥,
所以P(M)=P(A∪B∪C)=P(A)+P(B)+P(C)
==,
故1张奖券的中奖概率为.
(2)设“1张奖券不中特等奖且不中一等奖”为事件N,则事件N与“1张奖券中特等奖或中一等奖”为对立事件,所以P(N)=1-P(A∪B)=1-=.
故1张奖券不中特等奖且不中一等奖的概率为.
18.(1)25小时;(2)0.3.
【分析】
(1)根据直方图,频率最大的区间中点横坐标为众数即可求众数;(2)由学习的周均时长不少于30小时的区间有、,它们的频率之和,即为该校学生学习的周均时长不少于30小时的概率.
【详解】
(1)根据直方图知:频率最大的区间中点横坐标即为众数,
∴由频率最大区间为,则众数为;
(2)由图知:不少于30小时的区间有、,
∴该校学生学习的周均时长不少于30小时的概率.
【点睛】
本题考查了根据直方图求众数、概率,应用了众数的概念、频率法求概率,属于简单题.
19.(1) ;(2)
【分析】
(1)由题意知李明通过面试的样本点有:;
(2)由这4道题目能否答对是独立的,且李明答对第1题、第2题、第3题、第4题的概率分别为,即可求得李明通过面试的概率
【详解】
(1) 李明能通过面试的样本空间中样本点:
(2)由(1)知,李明通过面试的概率
,
又这4道题目能否答对是独立的,且李明答对第1题、第2题、第3题、第4题的概率分别为
∴,,
,,,
即.
【点睛】
本题考查了概率的概念及独立事件的概念计算,由题意任意答对3个及以上的题可通过面试即可写出通过面试的所有样本点,根据基本事件的独立性,利用独立事件的乘法概率公式求样本点概率,进而求得通过面试的概率
20.(1);(2).
【分析】
(1)根据消费次数表,利用频率估计概率;
(2)分别求出4次消费的利润,再求其平均值即可.
【详解】
(1)根据消费次数表,估计1位会员至少消费两次的概率;
(2)第1次消费利润;
第2次消费利润;
第3次消费利润;
第4次消费利润;
这4次消费获得的平均利润:.
【点睛】
本题考查利用频率估计概率,考查平均值的计算,属于简单题.
21.(1)见解析(2)贫困地区和发达地区参加测试的儿童得60分以上的概率分别为0.5和0.55.
【分析】
(1)根据所给表格,依次计算各组对应的频率值即可.
(2)随着测试人数的上升,可知频率值趋近于某个值,即为概率值.
【详解】
(1)根据频率计算公式,可得如下表所示:
贫困地区
参加测试的人数 30 50 100 200 500 800
得60分以上的人数 16 27 52 104 256 402
得60分以上的频率 0.533 0.540 0.520 0.520 0.512 0.503
发达地区
参加测试的人数 30 50 100 200 500 800
得60分以上的人数 17 29 56 111 276 440
得60分以上的频率 0.567 0.580 0.560 0.555 0.552 0.550
(2)随着测试人数的增加,两个地区参加测试的儿童得60分以上的频率逐渐趋近于0.5和0.55.
故贫困地区和发达地区参加测试的儿童得60分以上的概率分别为0.5和0.55.
【点睛】
本题考查了具体问题中频率的求法,频率与概率的关系,属于基础题.
22.(1)a=10,b=;面试分数的平均值为120分;(2).
【分析】
(1)由已知及频率分布表即可求参数,进而根据所得表格数据求平均值即可.
(2)列举出25~30号学生的所有可能的两人组合,根据折线图有25,26,27这三个号的学生面试分数均在200分以上,即可求概率.
【详解】
(1)面试分数在[100,200)内的学生共有30-15-4-1=10(名),故a=10,b==,
估计这些学生面试分数的平均值为50×+150×+250×+350×=120(分).
(2)从25~30号学生中任选两人的选择方法有(25,26),(25,27),(25,28),(25,29),(25,30),(26,27),(26,28),(26,29),(26,30),(27,28),(27,29),(27,30),(28,29),(28,30),(29,30)共15种,而由折线图知:25号,26号,27号学生的面试分数均在200分以上,
∴选择的两人的面试分数均在200分以上的选择方法有(25,26),(25,27),(26,27)共3种,故选择的两人的面试分数均在200分以上的概率为,即.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
