五年级上册数学 第12讲 组合图形的面积(一)精讲学案 人教版
文档属性
| 名称 | 五年级上册数学 第12讲 组合图形的面积(一)精讲学案 人教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 212.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-16 10:43:16 | ||
图片预览


文档简介
组合图形的面积(一)
巧思导航
第四章基本图形的面积:
三角形的面积=
平行四边形的面积=
长方形的面积=
正方形的面积=
梯形的面积=
高相等的两个平行四边形,底是几倍关系,面积就是几倍关系。
第六章组合图形的面积:
将所有图形转换成学过的基本图形进行计算。
方法一:分割法。
方法二:添补法。
方法三:割补法
数格子法计算不规则图形的面积
数格子时,把大于半格的算为1格,小于半格的不算。
公顷、平方千米单位换算:
边长为100m的正方形土地,它的面积是1公顷,即1公顷=10000㎡。
例如:学校跑道的面积为1公顷。
边长为1000m的正方形土地,它的面积是1平方千米,即1km2=1000000㎡。
例如:两个天安门广场的面积为1平方千米。
3.大变小,乘就好;小变大,除一下。
巧思精讲
例1:动手画。
将下面的梯形分割成一个平行四边形和一个三角形。(画出两种不同的分法。)
把下面各个图形分成我们已学过的图形(正方形、长方形、平行四边形、三角形或梯形)。
巧思精练1
计算组合图形的面积时,我们总是想办法将(
)图形分成一些(
)图形来计算,这个过程中用到的数学思想方法是(
)。
任何一个平行四边形,都一定可以分成两个完全相同的(
)、(
)、(
)。
巧思精练2
一个梯形的高是6分米,上底和下底的和是8分米,那么面积是(
)。
一个三角形与平行四边形的高和面积分别相等,平行四边形的底是20厘米,那么这个三角形的底边长(
)。
一个平行四边形面积是90cm2,若它的底和高都扩大2倍,它的面积是(
)cm2。
例2:下列图形的面积大约是多少?(每个小方格的面积为1m2)
(1)面积约是
m2,合计
公顷。(2)面积约是
m2,合计
公顷。
巧思精练1
单位换算。
20米=(
)分米=(
)厘米
1.5平方千米=(
)公顷
1500平方厘米=(
)平方分米=(
)平方米
120公顷=(
)平方千米
5.64公顷=(
)平方米
456000平方米=(
)公顷
1.2平方米=(
)平方厘米
8平方米=(
)平方分米=(
)平方厘米
巧思精练2
(1)一块梯形的果园,阳阳妈妈准备拿来种水果树,已知梯形的上底是50米,下底是80米,高是100米,这个果园有多少公顷?
(2)有一个三角形的大型停车场,占地0.8平方千米,已知每辆车占地16平方米,问可以停多少辆车?
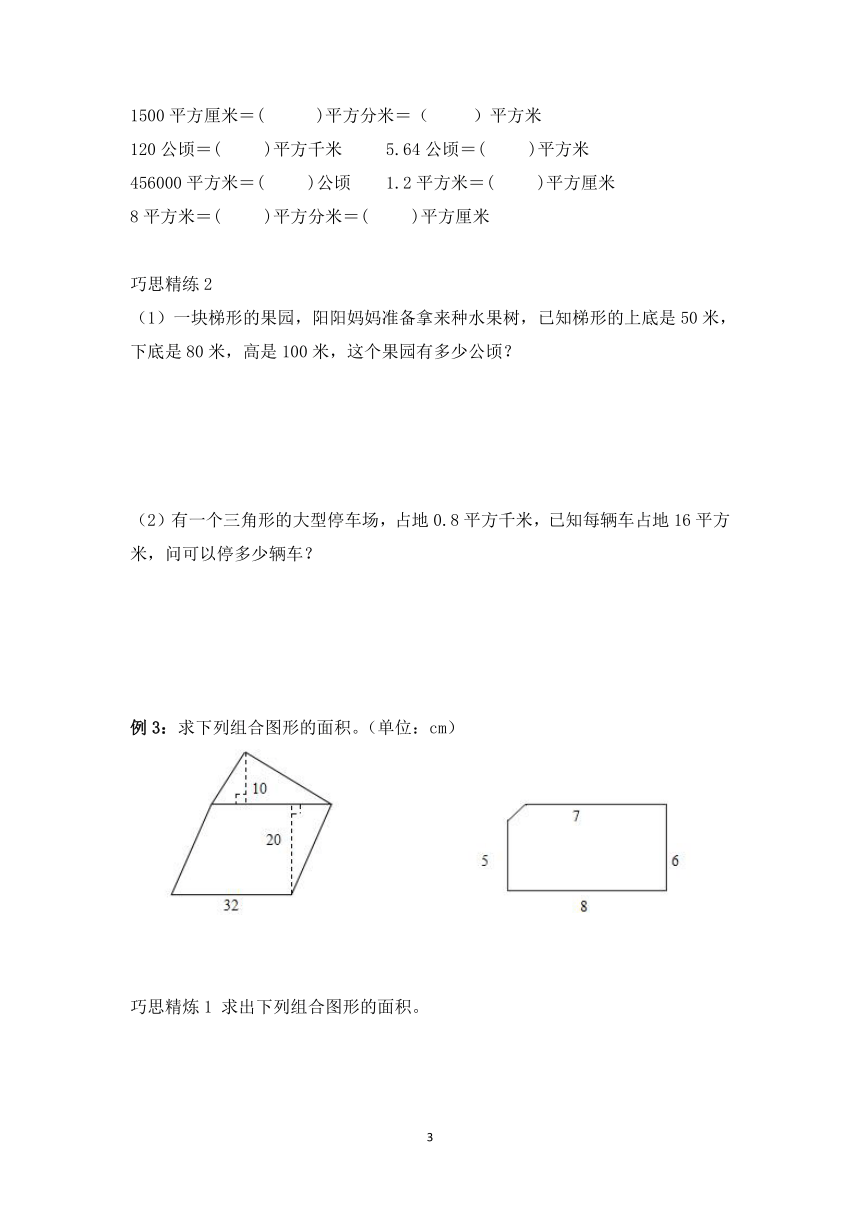
例3:求下列组合图形的面积。(单位:cm)
巧思精炼1
求出下列组合图形的面积。
巧思精炼2计算图形的面积。
例4:求下列图形的面积。(单位:cm)
巧思精炼1
下图的平行四边形面积是40平方厘米,求阴影部分的面积。(单位:厘米)
巧思精炼2
求下列图形的面积。
例5:一个直角梯形如右图,如果将上底延长4分米,就得到一个正方形,这个梯形的面积是多少dm2?
巧思精炼1
一个直角梯形的下底长是20cm,如果上底长再增加4cm就成了正方形,这个梯形的上底长是(
)cm,面积是(
)cm2。
巧思精炼2
已知一个梯形的上底是5cm,下底是8cm,将它的上底和下底各延长5cm,面积就增加20cm2,原来梯形的面积是多少cm2?
例6:如图所示,公园中间有一块长方形草地,中间有两条均匀的小路。求草地的实际面积。
巧思精炼1
一条白色正方形的手帕,它的边长是18厘米,手帕上横、竖各有两条红色的花纹(阴影所示),红条的宽都是2厘米。问这个手帕白色部分的面积是多少平方厘米?
巧思精炼2
某梯形农场中间修了三条宽为2米的小路,如图所示,已知梯形的上底是83米,下底是101米,高是54米,农场草地的面积是多少?合多少公顷?
例7:一块铁板的形状如下图。在这块铁板的两面涂上油漆,涂油漆的面积是多少?若每平方厘米用油漆5克,那么共需油漆多少克?(单位:厘米)
巧思精炼1
李大伯在一块多边形的地上分别种上红萝卜、青瓜和白菜(如图),求这三种菜各占地面积是多少平方米?若每公顷收蔬菜1500千克,这块地一共可以收多少千克蔬菜?
巧思精炼2
一块长方形的停车场,从长边的中点到两个宽边的中点分别连一条线,沿这两条线剪下来两个角。求剩下图形的面积是多少?已知一量车占地5平方米,最多可以放多少辆车?
巧思导航
第四章基本图形的面积:
三角形的面积=
平行四边形的面积=
长方形的面积=
正方形的面积=
梯形的面积=
高相等的两个平行四边形,底是几倍关系,面积就是几倍关系。
第六章组合图形的面积:
将所有图形转换成学过的基本图形进行计算。
方法一:分割法。
方法二:添补法。
方法三:割补法
数格子法计算不规则图形的面积
数格子时,把大于半格的算为1格,小于半格的不算。
公顷、平方千米单位换算:
边长为100m的正方形土地,它的面积是1公顷,即1公顷=10000㎡。
例如:学校跑道的面积为1公顷。
边长为1000m的正方形土地,它的面积是1平方千米,即1km2=1000000㎡。
例如:两个天安门广场的面积为1平方千米。
3.大变小,乘就好;小变大,除一下。
巧思精讲
例1:动手画。
将下面的梯形分割成一个平行四边形和一个三角形。(画出两种不同的分法。)
把下面各个图形分成我们已学过的图形(正方形、长方形、平行四边形、三角形或梯形)。
巧思精练1
计算组合图形的面积时,我们总是想办法将(
)图形分成一些(
)图形来计算,这个过程中用到的数学思想方法是(
)。
任何一个平行四边形,都一定可以分成两个完全相同的(
)、(
)、(
)。
巧思精练2
一个梯形的高是6分米,上底和下底的和是8分米,那么面积是(
)。
一个三角形与平行四边形的高和面积分别相等,平行四边形的底是20厘米,那么这个三角形的底边长(
)。
一个平行四边形面积是90cm2,若它的底和高都扩大2倍,它的面积是(
)cm2。
例2:下列图形的面积大约是多少?(每个小方格的面积为1m2)
(1)面积约是
m2,合计
公顷。(2)面积约是
m2,合计
公顷。
巧思精练1
单位换算。
20米=(
)分米=(
)厘米
1.5平方千米=(
)公顷
1500平方厘米=(
)平方分米=(
)平方米
120公顷=(
)平方千米
5.64公顷=(
)平方米
456000平方米=(
)公顷
1.2平方米=(
)平方厘米
8平方米=(
)平方分米=(
)平方厘米
巧思精练2
(1)一块梯形的果园,阳阳妈妈准备拿来种水果树,已知梯形的上底是50米,下底是80米,高是100米,这个果园有多少公顷?
(2)有一个三角形的大型停车场,占地0.8平方千米,已知每辆车占地16平方米,问可以停多少辆车?
例3:求下列组合图形的面积。(单位:cm)
巧思精炼1
求出下列组合图形的面积。
巧思精炼2计算图形的面积。
例4:求下列图形的面积。(单位:cm)
巧思精炼1
下图的平行四边形面积是40平方厘米,求阴影部分的面积。(单位:厘米)
巧思精炼2
求下列图形的面积。
例5:一个直角梯形如右图,如果将上底延长4分米,就得到一个正方形,这个梯形的面积是多少dm2?
巧思精炼1
一个直角梯形的下底长是20cm,如果上底长再增加4cm就成了正方形,这个梯形的上底长是(
)cm,面积是(
)cm2。
巧思精炼2
已知一个梯形的上底是5cm,下底是8cm,将它的上底和下底各延长5cm,面积就增加20cm2,原来梯形的面积是多少cm2?
例6:如图所示,公园中间有一块长方形草地,中间有两条均匀的小路。求草地的实际面积。
巧思精炼1
一条白色正方形的手帕,它的边长是18厘米,手帕上横、竖各有两条红色的花纹(阴影所示),红条的宽都是2厘米。问这个手帕白色部分的面积是多少平方厘米?
巧思精炼2
某梯形农场中间修了三条宽为2米的小路,如图所示,已知梯形的上底是83米,下底是101米,高是54米,农场草地的面积是多少?合多少公顷?
例7:一块铁板的形状如下图。在这块铁板的两面涂上油漆,涂油漆的面积是多少?若每平方厘米用油漆5克,那么共需油漆多少克?(单位:厘米)
巧思精炼1
李大伯在一块多边形的地上分别种上红萝卜、青瓜和白菜(如图),求这三种菜各占地面积是多少平方米?若每公顷收蔬菜1500千克,这块地一共可以收多少千克蔬菜?
巧思精炼2
一块长方形的停车场,从长边的中点到两个宽边的中点分别连一条线,沿这两条线剪下来两个角。求剩下图形的面积是多少?已知一量车占地5平方米,最多可以放多少辆车?
