2020-2021学年九年级数学人教版下册28.1 锐角三角函数(一) 训练(Word版,含答案)
文档属性
| 名称 | 2020-2021学年九年级数学人教版下册28.1 锐角三角函数(一) 训练(Word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 40.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-15 23:26:24 | ||
图片预览

文档简介
28.1 锐角三角函数(一)
【笔记】
1.在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a,b,c,则sinA=______;sinB=______.
2.有关正弦函数的注意点:
(1)sinA不是sin与A的乘积,而是一个整体;
(2)sinA是线段之间的一个比值,sinA没有单位.
【训练】
1.三角形在正方形网格纸中的位置如图所示,则sinα的值是( )
A. B.2 C. D.
第1题图
2.如图,在△ABC中,∠C=90°,AB=5,BC=3,则sinA的值是( )
第2题图
A. B. C. D.
3.如图,点A,B,C在⊙O上,∠ACB=30°,则sin∠AOB的值是( )
A. B.
C. D.
第3题图
4.在Rt△ABC中,∠C=90°,AC∶BC=1∶2,则sinB的值为( )
A. B. C. D.
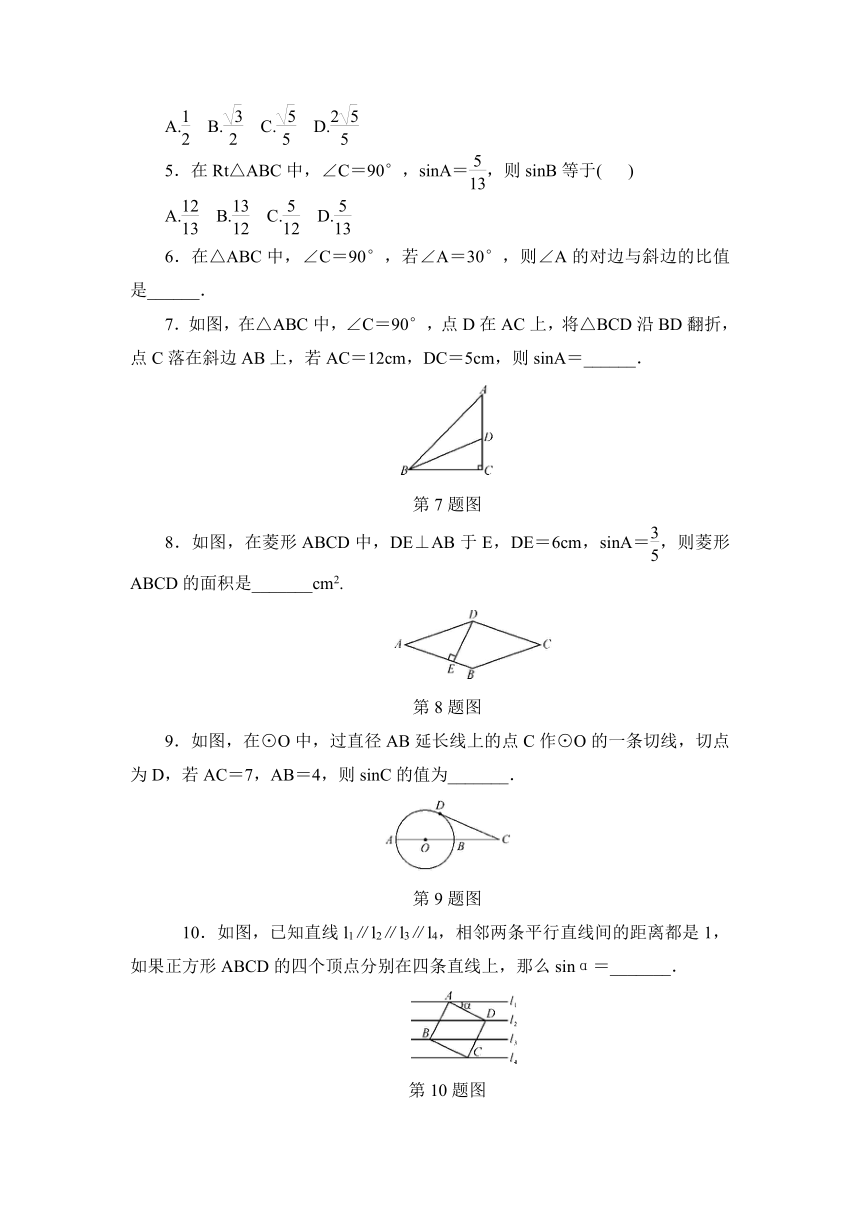
5.在Rt△ABC中,∠C=90°,sinA=,则sinB等于( )
A. B. C. D.
6.在△ABC中,∠C=90°,若∠A=30°,则∠A的对边与斜边的比值是______.
7.如图,在△ABC中,∠C=90°,点D在AC上,将△BCD沿BD翻折,点C落在斜边AB上,若AC=12cm,DC=5cm,则sinA=______.
第7题图
8.如图,在菱形ABCD中,DE⊥AB于E,DE=6cm,sinA=,则菱形ABCD的面积是_______cm2.
第8题图
9.如图,在⊙O中,过直径AB延长线上的点C作⊙O的一条切线,切点为D,若AC=7,AB=4,则sinC的值为_______.
第9题图
10.如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,那么sinα=_______.
第10题图
11.Rt△ABC中,若∠C=90°,a=15,b=8,求sinA+sinB.
12.如图所示,△ABC中,∠C=90°,sinA=,AC=2,求AB,BC的长.
第12题图
13.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=,AC=2,则sinB的值是( )
第13题图
A. B. C. D.
14.在Rt△ABC中,∠C=90°,a,b,c分别为∠A、∠B、∠C的对边,且a∶b=3∶4,则sinA∶sinB=______.
15.如图,在△ABC中,AD是BC边上的高,∠C=45°,sinB=,AD=1,求BC的长.
16.如图,已知⊙O的半径为2,弦BC的长为2,点A为弦BC所对优弧上任意一点(B,C两点除外).
第16题图
(1)求∠BAC的度数;
(2)求△ABC面积的最大值.
(参考数据:sin60°=,cos30°=)
答案
【课堂笔记】
1.
【课时训练】
1—5.ACCCA 6. 7. 8.60 9. 10.
11.由勾股定理得c===17,于是sinA=,sinB=,所以sinA+sinB=+=.
12.∵sinA=,∴=,∴AB=3BC.∵AC2+BC2=AB2,∴22+BC2=(3BC)2,∴BC=,∴AB=.
13. D
14.
15. 在Rt△ABD中,∵sinB==,又∵AD=1,∴AB=3,∵BD2=AB2-AD2,∴BD==2.在Rt△ADC中,∵∠C=45°,∴CD=AD=1.∴BC=BD+DC=2+1.
16. (1)过点O作OD⊥BC于点D,连接OC,OB.因为BC=2,所以CD=BC=.又因为OC=2,所以sin∠DOC==,所以∠DOC=60°,所以∠BOC=2∠DOC=120°,所以∠BAC=∠BOC=60°.
(2)因为△ABC中的边BC的长不变,所以底边上的高最大时,△ABC的面积最大,即点A是的中点时,△ABC的面积最大,此时=,所以AB=AC.又因为∠BAC=60°,所以△ABC是等边三角形.连接AD,易证AD是△ABC的高.在Rt△ADC中,AC=BC=2,CD=,所以AD===3,所以△ABC面积的最大值为×2×3=3.
【笔记】
1.在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a,b,c,则sinA=______;sinB=______.
2.有关正弦函数的注意点:
(1)sinA不是sin与A的乘积,而是一个整体;
(2)sinA是线段之间的一个比值,sinA没有单位.
【训练】
1.三角形在正方形网格纸中的位置如图所示,则sinα的值是( )
A. B.2 C. D.
第1题图
2.如图,在△ABC中,∠C=90°,AB=5,BC=3,则sinA的值是( )
第2题图
A. B. C. D.
3.如图,点A,B,C在⊙O上,∠ACB=30°,则sin∠AOB的值是( )
A. B.
C. D.
第3题图
4.在Rt△ABC中,∠C=90°,AC∶BC=1∶2,则sinB的值为( )
A. B. C. D.
5.在Rt△ABC中,∠C=90°,sinA=,则sinB等于( )
A. B. C. D.
6.在△ABC中,∠C=90°,若∠A=30°,则∠A的对边与斜边的比值是______.
7.如图,在△ABC中,∠C=90°,点D在AC上,将△BCD沿BD翻折,点C落在斜边AB上,若AC=12cm,DC=5cm,则sinA=______.
第7题图
8.如图,在菱形ABCD中,DE⊥AB于E,DE=6cm,sinA=,则菱形ABCD的面积是_______cm2.
第8题图
9.如图,在⊙O中,过直径AB延长线上的点C作⊙O的一条切线,切点为D,若AC=7,AB=4,则sinC的值为_______.
第9题图
10.如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,那么sinα=_______.
第10题图
11.Rt△ABC中,若∠C=90°,a=15,b=8,求sinA+sinB.
12.如图所示,△ABC中,∠C=90°,sinA=,AC=2,求AB,BC的长.
第12题图
13.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=,AC=2,则sinB的值是( )
第13题图
A. B. C. D.
14.在Rt△ABC中,∠C=90°,a,b,c分别为∠A、∠B、∠C的对边,且a∶b=3∶4,则sinA∶sinB=______.
15.如图,在△ABC中,AD是BC边上的高,∠C=45°,sinB=,AD=1,求BC的长.
16.如图,已知⊙O的半径为2,弦BC的长为2,点A为弦BC所对优弧上任意一点(B,C两点除外).
第16题图
(1)求∠BAC的度数;
(2)求△ABC面积的最大值.
(参考数据:sin60°=,cos30°=)
答案
【课堂笔记】
1.
【课时训练】
1—5.ACCCA 6. 7. 8.60 9. 10.
11.由勾股定理得c===17,于是sinA=,sinB=,所以sinA+sinB=+=.
12.∵sinA=,∴=,∴AB=3BC.∵AC2+BC2=AB2,∴22+BC2=(3BC)2,∴BC=,∴AB=.
13. D
14.
15. 在Rt△ABD中,∵sinB==,又∵AD=1,∴AB=3,∵BD2=AB2-AD2,∴BD==2.在Rt△ADC中,∵∠C=45°,∴CD=AD=1.∴BC=BD+DC=2+1.
16. (1)过点O作OD⊥BC于点D,连接OC,OB.因为BC=2,所以CD=BC=.又因为OC=2,所以sin∠DOC==,所以∠DOC=60°,所以∠BOC=2∠DOC=120°,所以∠BAC=∠BOC=60°.
(2)因为△ABC中的边BC的长不变,所以底边上的高最大时,△ABC的面积最大,即点A是的中点时,△ABC的面积最大,此时=,所以AB=AC.又因为∠BAC=60°,所以△ABC是等边三角形.连接AD,易证AD是△ABC的高.在Rt△ADC中,AC=BC=2,CD=,所以AD===3,所以△ABC面积的最大值为×2×3=3.
