2020-2021学年九年级数学人教版下册 28.2.2 应用举例(一) 训练(word版含答案)
文档属性
| 名称 | 2020-2021学年九年级数学人教版下册 28.2.2 应用举例(一) 训练(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 249.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-24 00:00:00 | ||
图片预览


文档简介
28.2.2 应用举例(一)
【笔记】
仰角和俯角
如图,在进行高度测量时,视线与水平线所成的角中,当视线在水平线上方时叫做________,当视线在水平线下方时叫做________.
【训练】
1.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,如果a2+b2=c2,那么下列结论正确的是( )
A.csinA=a B.bcosB=c
C.atanA=b D.ctanB=b
2.如图,小亮为了测量校园里教学楼AB的高度,将测角仪CD竖直放置在与教学楼水平距离为18m的地面上,若测角仪的高度为1.5m,测得教学楼的顶部A处的仰角为30°,则教学楼的高度是( )
A.55.5m B.54m C.19.5m D.18m
第2题图 第3题图
3.如图,电线杆CD的高度为h,两根拉线AC与BC互相垂直,∠CAB=α,则拉线BC的长度为(点A,D,B在同一条直线上)( )
A. B. C. D.h·cosα
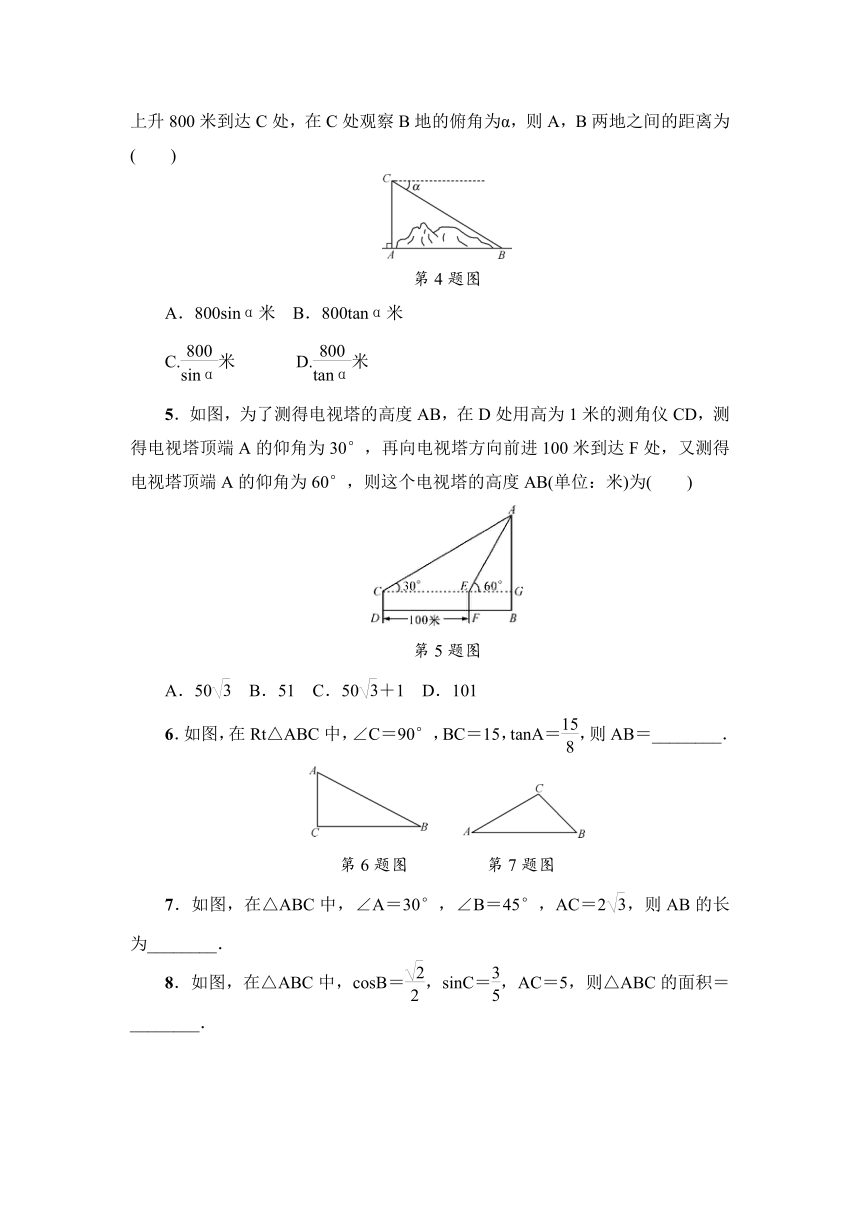
4.如图,某地修建高速公路,要从A地向B地修一条隧道(点A,B在同一水平面上).为了测量A,B两地之间的距离,一架直升机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A,B两地之间的距离为( )
第4题图
A.800sinα米 B.800tanα米
C.米 D.米
5.如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米到达F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
第5题图
A.50 B.51 C.50+1 D.101
6.如图,在Rt△ABC中,∠C=90°,BC=15,tanA=,则AB=________.
第6题图 第7题图
7.如图,在△ABC中,∠A=30°,∠B=45°,AC=2,则AB的长为________.
8.如图,在△ABC中,cosB=,sinC=,AC=5,则△ABC的面积=________.
第8题图 第9题图
9.如图,为测量河宽AB(假设河的两岸平行),在点C处测得∠ACB=30°,在点D处测得∠ADB=60°,且CD=60m,则河宽AB为________m(结果保留根号).
4219575132778510.如图,随着铁路建设进程的加快,现计划从A地到B地修建一条笔直的铁路,但在附近的C处有一大型油库,现测得油库C在A地的北偏东60°方向上,在B地的西北方向上,A,B两地之间的距离为250(+1)米.已知在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响.若在此路段修建铁路,油库C是否会受到影响?请说明理由.
4219575128968511.如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据≈1.4,≈1.7)
42195758001012.小明去爬山,在山脚看山顶角度为30°,小明在坡比为5∶12的山坡上走1300米,此时小明看山顶的角度为60°,则山高( )
A.(600-250)米 B.(600-250)米
C.(350+350)米 D.500米
13.如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m,CD=20m,AB和CD之间有一观景池,小南在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°(点B、E、D在同一直线上),求两幢建筑物之间的距离BD.(结果精确到0.1m)
第13题图
14.小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2,使用时为了散热,她在底板下垫入散热架ACO′后,电脑转到AO′B′位置(如图3),侧面示意图为图4.已知OA=OB=24,O′C⊥AC于点C,O′C=12cm.
第14题图
(1)求∠CAO′的度数;
(2)显示屏的顶部B′比原来升高了多少?
(3)如图4,垫入散热架后,要使显示屏O′B′与水平线的夹角仍保持120°,则显示屏O′B′应绕点O′按顺时针方向旋转多少度?
答案
【笔记】
仰角 俯角
【训练】
1—5.ACBDC
6.17 7.3+ 8.10.5 9. 30
第10题图
10. 油库C不会受到影响.理由如下:如图,过点C作CD⊥AB于点D,∴AD==CD,BD==CD.
∵AD+BD=AB=250(+1)米,∴CD+CD=250(+1)米,∴CD=250米,而250米>200米,故在此路段修建铁路,油库C不会受到影响.
11.在直角△ABD中,BD===41(米),则DF=BD-OE=(41-10)米,CF=DF+CD=41-10+40=(41+30)米,则在直角△CEF中,EF=CF·tanα=41+30≈41×1.7+30=99.7≈100(米).答:点E离地面的高度EF是100米.
12. B
13. 由题意得:∠AEB=42°,∠DEC=45°.
∵AB⊥BD,DC⊥BD,∴在Rt△ABE中,∠ABE=90°,AB=15,∠AEB=42°,∵tan∠AEB=,∴BE=≈15÷0.90=.
在Rt△DEC中,∠CDE=90°,∠DEC=∠DCE=45°,CD=20,∴ED=CD=20,∴BD=BE+ED=+20≈36.7m.
答:两幢建筑物之间的距离BD约为36.7m.
14.
(1)∵O′C⊥AC,OA=OB=24cm,
∴sin∠CAO′====.
∴∠CAO′=30°.
(2)如图,过点B作BD⊥AO交AO的延长线于点D.
∵sin∠BOD=,∴BD=OB·sin∠BOD.
∵∠AOB=120°,∴∠DOB=60°.
∴BD=OB·sin∠BOD=24×=12(cm).
∵O′C⊥AC,∠CAO′=30°,∴∠AO′C=60°.
又∵∠AO′B′=∠AOB=120°.∴∠AO′B′+∠AO′C=180°.
∴O′B′+O′C-BD=24+12-12=(36-12)cm.
∴显示屏的顶部B′比原来升高了(36-12)cm.
(3)显示屏O′B′应绕点O′按顺时针方向旋转30°.理由如下:电脑显示屏O′B′绕点O′按顺时针方向旋转α度至O′E处,O′F∥OA.
∵显示屏O′B′与水平线的夹角仍要保持120°,∴∠EO′F=120°.
∴∠FO′A=∠CAO′=30°.
∵∠AO′B′=120°,∴∠EO′B′=∠FO′A=30°.即α=30°,∴显示屏O′B′应绕点O′按顺时针方向旋转30°.
【笔记】
仰角和俯角
如图,在进行高度测量时,视线与水平线所成的角中,当视线在水平线上方时叫做________,当视线在水平线下方时叫做________.
【训练】
1.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,如果a2+b2=c2,那么下列结论正确的是( )
A.csinA=a B.bcosB=c
C.atanA=b D.ctanB=b
2.如图,小亮为了测量校园里教学楼AB的高度,将测角仪CD竖直放置在与教学楼水平距离为18m的地面上,若测角仪的高度为1.5m,测得教学楼的顶部A处的仰角为30°,则教学楼的高度是( )
A.55.5m B.54m C.19.5m D.18m
第2题图 第3题图
3.如图,电线杆CD的高度为h,两根拉线AC与BC互相垂直,∠CAB=α,则拉线BC的长度为(点A,D,B在同一条直线上)( )
A. B. C. D.h·cosα
4.如图,某地修建高速公路,要从A地向B地修一条隧道(点A,B在同一水平面上).为了测量A,B两地之间的距离,一架直升机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A,B两地之间的距离为( )
第4题图
A.800sinα米 B.800tanα米
C.米 D.米
5.如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米到达F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
第5题图
A.50 B.51 C.50+1 D.101
6.如图,在Rt△ABC中,∠C=90°,BC=15,tanA=,则AB=________.
第6题图 第7题图
7.如图,在△ABC中,∠A=30°,∠B=45°,AC=2,则AB的长为________.
8.如图,在△ABC中,cosB=,sinC=,AC=5,则△ABC的面积=________.
第8题图 第9题图
9.如图,为测量河宽AB(假设河的两岸平行),在点C处测得∠ACB=30°,在点D处测得∠ADB=60°,且CD=60m,则河宽AB为________m(结果保留根号).
4219575132778510.如图,随着铁路建设进程的加快,现计划从A地到B地修建一条笔直的铁路,但在附近的C处有一大型油库,现测得油库C在A地的北偏东60°方向上,在B地的西北方向上,A,B两地之间的距离为250(+1)米.已知在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响.若在此路段修建铁路,油库C是否会受到影响?请说明理由.
4219575128968511.如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据≈1.4,≈1.7)
42195758001012.小明去爬山,在山脚看山顶角度为30°,小明在坡比为5∶12的山坡上走1300米,此时小明看山顶的角度为60°,则山高( )
A.(600-250)米 B.(600-250)米
C.(350+350)米 D.500米
13.如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m,CD=20m,AB和CD之间有一观景池,小南在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°(点B、E、D在同一直线上),求两幢建筑物之间的距离BD.(结果精确到0.1m)
第13题图
14.小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2,使用时为了散热,她在底板下垫入散热架ACO′后,电脑转到AO′B′位置(如图3),侧面示意图为图4.已知OA=OB=24,O′C⊥AC于点C,O′C=12cm.
第14题图
(1)求∠CAO′的度数;
(2)显示屏的顶部B′比原来升高了多少?
(3)如图4,垫入散热架后,要使显示屏O′B′与水平线的夹角仍保持120°,则显示屏O′B′应绕点O′按顺时针方向旋转多少度?
答案
【笔记】
仰角 俯角
【训练】
1—5.ACBDC
6.17 7.3+ 8.10.5 9. 30
第10题图
10. 油库C不会受到影响.理由如下:如图,过点C作CD⊥AB于点D,∴AD==CD,BD==CD.
∵AD+BD=AB=250(+1)米,∴CD+CD=250(+1)米,∴CD=250米,而250米>200米,故在此路段修建铁路,油库C不会受到影响.
11.在直角△ABD中,BD===41(米),则DF=BD-OE=(41-10)米,CF=DF+CD=41-10+40=(41+30)米,则在直角△CEF中,EF=CF·tanα=41+30≈41×1.7+30=99.7≈100(米).答:点E离地面的高度EF是100米.
12. B
13. 由题意得:∠AEB=42°,∠DEC=45°.
∵AB⊥BD,DC⊥BD,∴在Rt△ABE中,∠ABE=90°,AB=15,∠AEB=42°,∵tan∠AEB=,∴BE=≈15÷0.90=.
在Rt△DEC中,∠CDE=90°,∠DEC=∠DCE=45°,CD=20,∴ED=CD=20,∴BD=BE+ED=+20≈36.7m.
答:两幢建筑物之间的距离BD约为36.7m.
14.
(1)∵O′C⊥AC,OA=OB=24cm,
∴sin∠CAO′====.
∴∠CAO′=30°.
(2)如图,过点B作BD⊥AO交AO的延长线于点D.
∵sin∠BOD=,∴BD=OB·sin∠BOD.
∵∠AOB=120°,∴∠DOB=60°.
∴BD=OB·sin∠BOD=24×=12(cm).
∵O′C⊥AC,∠CAO′=30°,∴∠AO′C=60°.
又∵∠AO′B′=∠AOB=120°.∴∠AO′B′+∠AO′C=180°.
∴O′B′+O′C-BD=24+12-12=(36-12)cm.
∴显示屏的顶部B′比原来升高了(36-12)cm.
(3)显示屏O′B′应绕点O′按顺时针方向旋转30°.理由如下:电脑显示屏O′B′绕点O′按顺时针方向旋转α度至O′E处,O′F∥OA.
∵显示屏O′B′与水平线的夹角仍要保持120°,∴∠EO′F=120°.
∴∠FO′A=∠CAO′=30°.
∵∠AO′B′=120°,∴∠EO′B′=∠FO′A=30°.即α=30°,∴显示屏O′B′应绕点O′按顺时针方向旋转30°.
