江苏省南京市鼓楼区2020-2021学年高一下学期期中考试数学试题 Word版含答案解析
文档属性
| 名称 | 江苏省南京市鼓楼区2020-2021学年高一下学期期中考试数学试题 Word版含答案解析 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-17 10:19:24 | ||
图片预览




文档简介
南京市鼓楼区2020~2021学年度第二学期高一(下)期中试卷
数学
注意事项:
1.本试卷考试时间为120分钟,试卷满分150分,考试形式闭卷.
2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.
3.答题前,务必将自已的姓名?准证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上.
第Ⅰ卷(选择题共60分)
一?单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.计算:false( )
A.false B.false C.false D.false
2.计算:复数false( )
A.false B.false C.false D.false
3.在△ABC中,角A?B,C的对边分别为a,b,c,若a:b:c=3:5:7,则其最大角的大小为( )
A.60° B.75° C.120° D.150°
4.托勒密(C.Ptolemy,约90-168),古希腊人,是天文学家?地理学家?地图学家?数学家,所著《天文集》第一卷中载有弦表.在弦表基础上,后人制作了正弦和余弦表(部分如下图所示),该表便于查出0°~90°间许多角的正弦值和余弦值,避免了冗长的计算.例如,依据该表,角2°12′的正弦值为0.0384,角30°0′的正弦值为0.5000,则角34°36′的正弦值为( )
A.0.0017 B.0.0454 C.0.5678 D.0.5736
5.在下列向量组中,可以把向量false表示出来的是( )
A.false
B.false
C.false
D.false
6.false是边长为2的等边三角形,已知向量false满足false,则false( )
A.1 B.false C.false D.false
7.化简false可得( )
A.false B.false
C.false D.false
8.已知false的内角false所对的边为false,其面积为false,若false且false的外接圆半径为false,则false周长的取值范围为( )
A.false B.false C.false D.false
二?多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对得5分,部分选对得2分,不选或有选错的的得0分)
9.在下列选项中,正确的是( )
A.false
B.false
C.存在角α,β,使得sin(α+β)D.对于任意角α,β,式子cos(α+β)10已知false是三个向量,在下列命题中,假命题是( )
A.false
B.false
C.false
D.若false则false
11.在false中,角false的对边分别为false,已知false,在下列选项中,正确的是( )
A.false B.false
C.false的取值范围为false D.当false时,则false,
12.在下列选项中正确的是( )
A.若z∈C,|z|2=z2,则z∈R
B.若z1,z2∈C,|z1+z2|=|z1-z2|,则z1z2=0
C.若复数false,则false
D.若复数z=(cos25°+isin25°)(cos65°+isin65°),则z=i
第Ⅱ卷(非选择题共90分)
三?填空题(本大题共4小题,每小题5分,共20分)
13.已知α为锐角,且false,则false______.
14.已知复数z满足|z-1-2i|=2,则|z|的最大值为______.
15.作用于同一点的三个力F1,F2,F3平衡.已知F1=4N,F2=5N,F1与F2之间的夹角是60°,则力F3的大小为______N.
16.如图,在矩形ABCD中,点E在边AD上,点F在边BC上,false,∠BFE=120°,EF=2.若△CEF的面积为false,则AB=________,sin∠BEC=________.
四?解答题(本大题共6小题,共70分.解答时应写出文字说明?证明过程或演算步骤)
17.(本小题满分10分)
(1)求false的值;
(2)求false的值.
18.(本小题满分12分)
已知z是复数,false+3i为实数(i为虚数单位),且false.
(1)求z;
(2)若z和(z+mi)2在复平面内对应的点都在第一象限,求实数m的取值范围.
19.(本小题满分12分)
在①a=7;②csinA=4;③false这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,则求出该三角形面积;若问题中的三角形不存在,则请说明理由.
问题:是否存在锐角三角形ABC,它的内角A,B,C的对边分别为a,b,c,且c=8,false,__________?
20.(本小题满分12分)
设函数false.
(1)求f(x)的最小正周期;
(2)设方程false在区间false内的两解分别为x1,x2,求cos(x1-x2)的值.
21.(本小题满分12分)
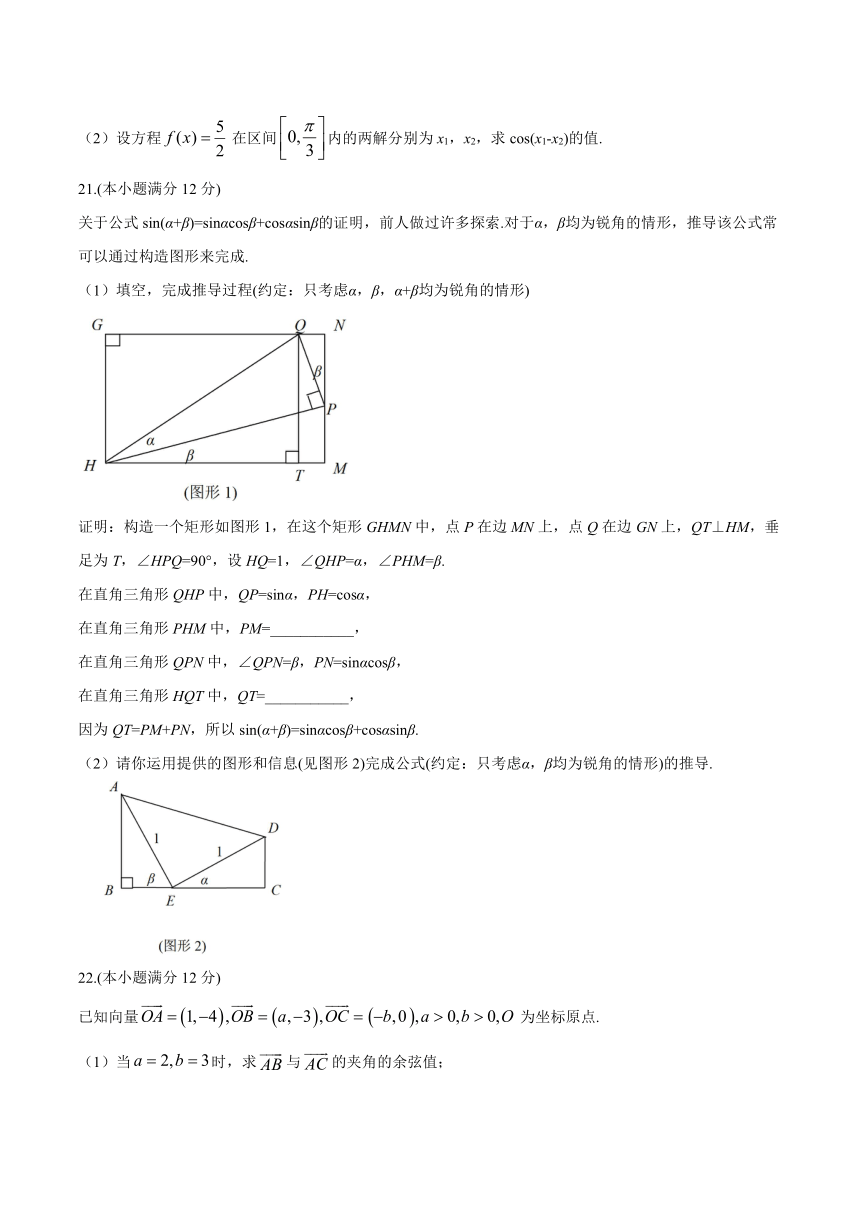
关于公式sin(α+β)=sinαcosβ+cosαsinβ的证明,前人做过许多探索.对于α,β均为锐角的情形,推导该公式常可以通过构造图形来完成.
(1)填空,完成推导过程(约定:只考虑α,β,α+β均为锐角的情形)
证明:构造一个矩形如图形1,在这个矩形GHMN中,点P在边MN上,点Q在边GN上,QT⊥HM,垂足为T,∠HPQ=90°,设HQ=1,∠QHP=α,∠PHM=β.
在直角三角形QHP中,QP=sinα,PH=cosα,
在直角三角形PHM中,PM=___________,
在直角三角形QPN中,∠QPN=β,PN=sinαcosβ,
在直角三角形HQT中,QT=___________,
因为QT=PM+PN,所以sin(α+β)=sinαcosβ+cosαsinβ.
(2)请你运用提供的图形和信息(见图形2)完成公式(约定:只考虑α,β均为锐角的情形)的推导.
22.(本小题满分12分)
已知向量false为坐标原点.
(1)当false时,求false与false的夹角的余弦值;
(2)若false三点共线,求false的最小值.
南京市鼓楼区2020~2021学年度第二学期高一(下)期中试卷
数学
注意事项:
1.本试卷考试时间为120分钟,试卷满分150分,考试形式闭卷.
2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.
3.答题前,务必将自已的姓名?准证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上.
第Ⅰ卷(选择题共60分)
一?单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.计算:false( )
A.false B.false C.false D.false
【答案】D
【考点】两角和与差的正弦公式
【解析】由题意可知,false,故答案选D
2.计算:复数false( )
A.false B.false C.false D.false
【答案】B
【考点】复数的运算
【解析】由题意可知,false,故答案选false.
3.在△ABC中,角A?B,C的对边分别为a,b,c,若a:b:c=3:5:7,则其最大角的大小为( )
A.60° B.75° C.120° D.150°
【答案】C
【考点】余弦定理的应用
【解析】由题意可知,false为最大边,且设false,则在false中,由余弦定理可得,false
false,又false,所以false,即最大角的大小为false,故答案选false
4.托勒密(C.Ptolemy,约90-168),古希腊人,是天文学家?地理学家?地图学家?数学家,所著《天文集》第一卷中载有弦表.在弦表基础上,后人制作了正弦和余弦表(部分如下图所示),该表便于查出0°~90°间许多角的正弦值和余弦值,避免了冗长的计算.例如,依据该表,角2°12′的正弦值为0.0384,角30°0′的正弦值为0.5000,则角34°36′的正弦值为( )
A.0.0017 B.0.0454 C.0.5678 D.0.5736
【答案】C
【考点】新情景问题下的文化题:三角函数值求解
【解析】由题意可知,查表可得false的正弦值为0.5678,故答案选C.
5.在下列向量组中,可以把向量false表示出来的是( )
A.false
B.false
C.false
D.false
【答案】A
【考点】平面向量的基本定理应用:基底的选取与向量的表示
【解析】由题意可知,平面向量的基底不共线,选项B中,afalseb,所以排除;选项C中,b=2a,即afalseb,所以排除;选项D中,a=-b,即afalseb,所以排除;选项A中,a与b不共线,则向量m=(-1,3)可以用a与b表示出来,所以选项A正确,故答案选A.
6.false是边长为2的等边三角形,已知向量false满足false,则false( )
A.1 B.false C.false D.false
【答案】B
【考点】平面向量的数量积运算
【解析】在false中,由false,可得false,则false,且false
false,所以false,解得false,故答案选false
7.化简false可得( )
A.false B.false
C.false D.false
【答案】B
【考点】三角恒等变换:二倍角公式?诱导公式的应用
【解析】由题意可知,falsefalse,故答案选false
8.已知false的内角false所对的边为false,其面积为false,若false且false的外接圆半径为false,则false周长的取值范围为( )
A.false B.false C.false D.false
【答案】A
【考点】正余弦定理的综合应用:求周长的范围问题
【解析】由题意可知,在false中,因为false,因为false,所以false,所以false,则由余弦定理可得,false,又false,所以falsefalse,则false,在false中,由正弦定理可得,false,则falsefalse,所以false周长false
false,因为false,所以falsefalse,所以false,则false周长false,故答案选false
二?多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对得5分,部分选对得2分,不选或有选错的的得0分)
9.在下列选项中,正确的是( )
A.false
B.false
C.存在角α,β,使得sin(α+β)D.对于任意角α,β,式子cos(α+β)【答案】BC
【考点】两角和与差的公式应用
【解析】由题意可知,对于选项A,false,所以选项false错误;对于选项false,所以选项false正确;对于选项C,当,false时false,所以false,所以false成立
,所以选项false正确;对于选项false,当false时falsefalse,所以选项false错误;综上,答案选false
10已知false是三个向量,在下列命题中,假命题是( )
A.false
B.false
C.false
D.若false则false
【答案】CD
【考点】平面向量的运算律应用
【解析】由题意可知,对于选项A,满足数量积的交换律,所以选项A正确;对于选项B,满足数量积的
分配律,所以选项B正确;对于选项C,a·b与b·c的结果均为数,则(a·b)·c与a·(b·c)的方向不一定相同,大小不一定相等,所以选项C错误;对于选项D,若a=0,则b与c不一定相等,所以选项D错误;综上,答案选CD.
11.在false中,角false的对边分别为false,已知false,在下列选项中,正确的是( )
A.false B.false
C.false的取值范围为false D.当false时,则false,
【答案】BCD
【考点】解三角形的综合应用
【解析】由题意可知,对于选项false,因为false,且false,所以联立解得false,则false,又因为false,
所以false解得false
所以选项false正确,选项false错误;对于选项false,由false,且false在false上单调递增,可得false,所以选项false正确;对于选项false,当false时,由正弦定理可得,false,又false,所以falsefalse,则解得false,所以选项false正确;综上,答案选false.
12.在下列选项中正确的是( )
A.若z∈C,|z|2=z2,则z∈R
B.若z1,z2∈C,|z1+z2|=|z1-z2|,则z1z2=0
C.若复数false,则false
D.若复数z=(cos25°+isin25°)(cos65°+isin65°),则z=i
【答案】ACD
【考点】复数的综合应用
【解析】由题意可知,对于选项false,可设false,则false,若,false,则false,所以false,所以选项false正确;对于选项false,设false,则falsefalse,若false,则false,而falsefalse,不一定得到false,所以选项false错误;对于选项false,若false,所以false,所以false,所以选项false正确;对于选项D,若falsefalse,所以选项false正确;综上,答案选false
第Ⅱ卷(非选择题共90分)
三?填空题(本大题共4小题,每小题5分,共20分)
13.已知α为锐角,且false,则false______.
【答案】false
【考点】同角三角函数关系?两角和与差的正切公式
【解析】由题意可知,false为锐角,且false,所以false,则false,所以falsefalse
14.已知复数z满足|z-1-2i|=2,则|z|的最大值为______.
【答案】false
【考点】复数的运算以及综合应用
【解析】由题意可设,false,由false,可得false,则false,即false,可令false,所以falsefalse为任意角,且false,当false时取到最大值,所以false的最大值为falsefalse
15.作用于同一点的三个力F1,F2,F3平衡.已知F1=4N,F2=5N,F1与F2之间的夹角是60°,则力F3的大小为______N.
【答案】false
【考点】正余弦定理在物理上的应用
【解析】由题意可知,三个力false平衡,则false与false的合力false与false等大反向,所以在false中,由余弦定理可得,false,即false
16.如图,在矩形ACD中,点E在边AD上,点F在边BC上,false,∠BFE=120°,EF=2.
若△CEF的面积为false,则AB=________,sin∠BEC=________.
【答案】false
【考点】双空题:正余弦定理在平面几何中的应用
【解析】由题意,因为false,所以false,则在false中,可得falsefalse,由false,可解得false,在false中,可得false,所以falsefalse又false,所以false,在false中,由余弦定理可得,false,解得falsefalse,在false中,由余弦定理可得,false
false,解得false,则在false中,falsefalse,则false
四?解答题(本大题共6小题,共70分.解答时应写出文字说明?证明过程或演算步骤)
17.(本小题满分10分)
(1)求false的值;
(2)求false的值.
【考点】平面向量的数量积的坐标运算?模的求解
【解析】
(1)由题意,因为false,所以false
所以false;
(2)由(1)知false,所以|2m+false,
所以|2m+false.
18.(本小题满分12分)
已知z是复数,false+3i为实数(i为虚数单位),且false.
(1)求z;
(2)若z和(z+mi)2在复平面内对应的点都在第一象限,求实数m的取值范围.
【考点】复数的运算?几何意义
【解析】(1)由题意可设false,则false,
又因为false为实数,所以false,
因为false,所以false,解得false,
所以false
(2)若false和false在复平面内对应的点都在第一象限,
则false,
所以有false,且false,解得一false,则实数false的取值范围为false
19.(本小题满分12分)
在①a=7;②csinA=4;③false这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,则求出该三角形面积;若问题中的三角形不存在,则请说明理由.
问题:是否存在锐角三角形ABC,它的内角A,B,C的对边分别为a,b,c,且c=8,false,__________?
【考点】结构不良题:解三角形与三角恒等变换综合应用
【解析】在false中,因为false,且false,
所以false,即false,
又因为false,所以false,所以false,
在false中,由false,可得false,
选①:由余弦定理可得false,即false,解得false或false,
所以false或103;
选②:false,故该三角形不存在;
选③:由false可得,false,
则由正弦定理可得,false,即false,
且false
所以false
20.(本小题满分12分)
设函数false.
(1)求f(x)的最小正周期;
(2)设方程false在区间false内的两解分别为x1,x2,求cos(x1-x2)的值.
【考点】三角函数的图像与性质?三角恒等变换给值求值问题
【解析】(1)由题意,false,
则false的最小正周期为false
(2)由(1)知false所以方程false可化为:false,
由false为方程false的两个根可得,false且false,
则在区间false内false,解得false,即false,
所以false
21.(本小题满分12分)
关于公式sin(α+β)=sinαcosβ+cosαsinβ的证明,前人做过许多探索.对于α,β均为锐角的情形,推导该公式常可以通过构造图形来完成.
(1)填空,完成推导过程(约定:只考虑α,β,α+β均为锐角的情形)
证明:构造一个矩形如图形1,在这个矩形GHMN中,点P在边MN上,点Q在边GN上,QT⊥HM,垂足为T,∠HPQ=90°,设HQ=1,∠QHP=α,∠PHM=β.
在直角三角形QHP中,QP=sinα,PH=cosα,
在直角三角形PHM中,PM=①,
在直角三角形QPN中,∠QPN=β,PN=sinαcosβ,
在直角三角形HQT中,QT=②,
因为QT=PM+PN,所以sin(α+β)=sinαcosβ+cosαsinβ.
(2)请你运用提供的图形和信息(见图形2)完成公式(约定:只考虑α,β均为锐角的情形)的推导.
【考点】开放性试题:两角和的正弦公式证明
【解析】(1)由题意可知,在直角三角形false中,false在直角三角形false中,falsefalse
(2)由题意可知,在false中,false,且false,
所以false,
在false中,false,所以false,
在false中,false,所以false,
又false,
所以false,
化简可得,false得证.
22.(本小题满分12分)
已知向量false为坐标原点.
(1)当false时,求false与false的夹角的余弦值;
(2)若false三点共线,求false的最小值.
【考点】平面向量数量积的坐标运算、平面向量共线的充要条件、基本不等式综合应用
【解析】(1)当false时false,
所以false
则false,
所以false;
(2)若false三点共线,则false,
又因为false,
则false,解得false,则false,
因为false,所以false,
所以false,
当且仅当false,即false时取等号,
所以false的最小值为false.
数学
注意事项:
1.本试卷考试时间为120分钟,试卷满分150分,考试形式闭卷.
2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.
3.答题前,务必将自已的姓名?准证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上.
第Ⅰ卷(选择题共60分)
一?单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.计算:false( )
A.false B.false C.false D.false
2.计算:复数false( )
A.false B.false C.false D.false
3.在△ABC中,角A?B,C的对边分别为a,b,c,若a:b:c=3:5:7,则其最大角的大小为( )
A.60° B.75° C.120° D.150°
4.托勒密(C.Ptolemy,约90-168),古希腊人,是天文学家?地理学家?地图学家?数学家,所著《天文集》第一卷中载有弦表.在弦表基础上,后人制作了正弦和余弦表(部分如下图所示),该表便于查出0°~90°间许多角的正弦值和余弦值,避免了冗长的计算.例如,依据该表,角2°12′的正弦值为0.0384,角30°0′的正弦值为0.5000,则角34°36′的正弦值为( )
A.0.0017 B.0.0454 C.0.5678 D.0.5736
5.在下列向量组中,可以把向量false表示出来的是( )
A.false
B.false
C.false
D.false
6.false是边长为2的等边三角形,已知向量false满足false,则false( )
A.1 B.false C.false D.false
7.化简false可得( )
A.false B.false
C.false D.false
8.已知false的内角false所对的边为false,其面积为false,若false且false的外接圆半径为false,则false周长的取值范围为( )
A.false B.false C.false D.false
二?多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对得5分,部分选对得2分,不选或有选错的的得0分)
9.在下列选项中,正确的是( )
A.false
B.false
C.存在角α,β,使得sin(α+β)
A.false
B.false
C.false
D.若false则false
11.在false中,角false的对边分别为false,已知false,在下列选项中,正确的是( )
A.false B.false
C.false的取值范围为false D.当false时,则false,
12.在下列选项中正确的是( )
A.若z∈C,|z|2=z2,则z∈R
B.若z1,z2∈C,|z1+z2|=|z1-z2|,则z1z2=0
C.若复数false,则false
D.若复数z=(cos25°+isin25°)(cos65°+isin65°),则z=i
第Ⅱ卷(非选择题共90分)
三?填空题(本大题共4小题,每小题5分,共20分)
13.已知α为锐角,且false,则false______.
14.已知复数z满足|z-1-2i|=2,则|z|的最大值为______.
15.作用于同一点的三个力F1,F2,F3平衡.已知F1=4N,F2=5N,F1与F2之间的夹角是60°,则力F3的大小为______N.
16.如图,在矩形ABCD中,点E在边AD上,点F在边BC上,false,∠BFE=120°,EF=2.若△CEF的面积为false,则AB=________,sin∠BEC=________.
四?解答题(本大题共6小题,共70分.解答时应写出文字说明?证明过程或演算步骤)
17.(本小题满分10分)
(1)求false的值;
(2)求false的值.
18.(本小题满分12分)
已知z是复数,false+3i为实数(i为虚数单位),且false.
(1)求z;
(2)若z和(z+mi)2在复平面内对应的点都在第一象限,求实数m的取值范围.
19.(本小题满分12分)
在①a=7;②csinA=4;③false这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,则求出该三角形面积;若问题中的三角形不存在,则请说明理由.
问题:是否存在锐角三角形ABC,它的内角A,B,C的对边分别为a,b,c,且c=8,false,__________?
20.(本小题满分12分)
设函数false.
(1)求f(x)的最小正周期;
(2)设方程false在区间false内的两解分别为x1,x2,求cos(x1-x2)的值.
21.(本小题满分12分)
关于公式sin(α+β)=sinαcosβ+cosαsinβ的证明,前人做过许多探索.对于α,β均为锐角的情形,推导该公式常可以通过构造图形来完成.
(1)填空,完成推导过程(约定:只考虑α,β,α+β均为锐角的情形)
证明:构造一个矩形如图形1,在这个矩形GHMN中,点P在边MN上,点Q在边GN上,QT⊥HM,垂足为T,∠HPQ=90°,设HQ=1,∠QHP=α,∠PHM=β.
在直角三角形QHP中,QP=sinα,PH=cosα,
在直角三角形PHM中,PM=___________,
在直角三角形QPN中,∠QPN=β,PN=sinαcosβ,
在直角三角形HQT中,QT=___________,
因为QT=PM+PN,所以sin(α+β)=sinαcosβ+cosαsinβ.
(2)请你运用提供的图形和信息(见图形2)完成公式(约定:只考虑α,β均为锐角的情形)的推导.
22.(本小题满分12分)
已知向量false为坐标原点.
(1)当false时,求false与false的夹角的余弦值;
(2)若false三点共线,求false的最小值.
南京市鼓楼区2020~2021学年度第二学期高一(下)期中试卷
数学
注意事项:
1.本试卷考试时间为120分钟,试卷满分150分,考试形式闭卷.
2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.
3.答题前,务必将自已的姓名?准证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上.
第Ⅰ卷(选择题共60分)
一?单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.计算:false( )
A.false B.false C.false D.false
【答案】D
【考点】两角和与差的正弦公式
【解析】由题意可知,false,故答案选D
2.计算:复数false( )
A.false B.false C.false D.false
【答案】B
【考点】复数的运算
【解析】由题意可知,false,故答案选false.
3.在△ABC中,角A?B,C的对边分别为a,b,c,若a:b:c=3:5:7,则其最大角的大小为( )
A.60° B.75° C.120° D.150°
【答案】C
【考点】余弦定理的应用
【解析】由题意可知,false为最大边,且设false,则在false中,由余弦定理可得,false
false,又false,所以false,即最大角的大小为false,故答案选false
4.托勒密(C.Ptolemy,约90-168),古希腊人,是天文学家?地理学家?地图学家?数学家,所著《天文集》第一卷中载有弦表.在弦表基础上,后人制作了正弦和余弦表(部分如下图所示),该表便于查出0°~90°间许多角的正弦值和余弦值,避免了冗长的计算.例如,依据该表,角2°12′的正弦值为0.0384,角30°0′的正弦值为0.5000,则角34°36′的正弦值为( )
A.0.0017 B.0.0454 C.0.5678 D.0.5736
【答案】C
【考点】新情景问题下的文化题:三角函数值求解
【解析】由题意可知,查表可得false的正弦值为0.5678,故答案选C.
5.在下列向量组中,可以把向量false表示出来的是( )
A.false
B.false
C.false
D.false
【答案】A
【考点】平面向量的基本定理应用:基底的选取与向量的表示
【解析】由题意可知,平面向量的基底不共线,选项B中,afalseb,所以排除;选项C中,b=2a,即afalseb,所以排除;选项D中,a=-b,即afalseb,所以排除;选项A中,a与b不共线,则向量m=(-1,3)可以用a与b表示出来,所以选项A正确,故答案选A.
6.false是边长为2的等边三角形,已知向量false满足false,则false( )
A.1 B.false C.false D.false
【答案】B
【考点】平面向量的数量积运算
【解析】在false中,由false,可得false,则false,且false
false,所以false,解得false,故答案选false
7.化简false可得( )
A.false B.false
C.false D.false
【答案】B
【考点】三角恒等变换:二倍角公式?诱导公式的应用
【解析】由题意可知,falsefalse,故答案选false
8.已知false的内角false所对的边为false,其面积为false,若false且false的外接圆半径为false,则false周长的取值范围为( )
A.false B.false C.false D.false
【答案】A
【考点】正余弦定理的综合应用:求周长的范围问题
【解析】由题意可知,在false中,因为false,因为false,所以false,所以false,则由余弦定理可得,false,又false,所以falsefalse,则false,在false中,由正弦定理可得,false,则falsefalse,所以false周长false
false,因为false,所以falsefalse,所以false,则false周长false,故答案选false
二?多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对得5分,部分选对得2分,不选或有选错的的得0分)
9.在下列选项中,正确的是( )
A.false
B.false
C.存在角α,β,使得sin(α+β)
【考点】两角和与差的公式应用
【解析】由题意可知,对于选项A,false,所以选项false错误;对于选项false,所以选项false正确;对于选项C,当,false时false,所以false,所以false成立
,所以选项false正确;对于选项false,当false时falsefalse,所以选项false错误;综上,答案选false
10已知false是三个向量,在下列命题中,假命题是( )
A.false
B.false
C.false
D.若false则false
【答案】CD
【考点】平面向量的运算律应用
【解析】由题意可知,对于选项A,满足数量积的交换律,所以选项A正确;对于选项B,满足数量积的
分配律,所以选项B正确;对于选项C,a·b与b·c的结果均为数,则(a·b)·c与a·(b·c)的方向不一定相同,大小不一定相等,所以选项C错误;对于选项D,若a=0,则b与c不一定相等,所以选项D错误;综上,答案选CD.
11.在false中,角false的对边分别为false,已知false,在下列选项中,正确的是( )
A.false B.false
C.false的取值范围为false D.当false时,则false,
【答案】BCD
【考点】解三角形的综合应用
【解析】由题意可知,对于选项false,因为false,且false,所以联立解得false,则false,又因为false,
所以false解得false
所以选项false正确,选项false错误;对于选项false,由false,且false在false上单调递增,可得false,所以选项false正确;对于选项false,当false时,由正弦定理可得,false,又false,所以falsefalse,则解得false,所以选项false正确;综上,答案选false.
12.在下列选项中正确的是( )
A.若z∈C,|z|2=z2,则z∈R
B.若z1,z2∈C,|z1+z2|=|z1-z2|,则z1z2=0
C.若复数false,则false
D.若复数z=(cos25°+isin25°)(cos65°+isin65°),则z=i
【答案】ACD
【考点】复数的综合应用
【解析】由题意可知,对于选项false,可设false,则false,若,false,则false,所以false,所以选项false正确;对于选项false,设false,则falsefalse,若false,则false,而falsefalse,不一定得到false,所以选项false错误;对于选项false,若false,所以false,所以false,所以选项false正确;对于选项D,若falsefalse,所以选项false正确;综上,答案选false
第Ⅱ卷(非选择题共90分)
三?填空题(本大题共4小题,每小题5分,共20分)
13.已知α为锐角,且false,则false______.
【答案】false
【考点】同角三角函数关系?两角和与差的正切公式
【解析】由题意可知,false为锐角,且false,所以false,则false,所以falsefalse
14.已知复数z满足|z-1-2i|=2,则|z|的最大值为______.
【答案】false
【考点】复数的运算以及综合应用
【解析】由题意可设,false,由false,可得false,则false,即false,可令false,所以falsefalse为任意角,且false,当false时取到最大值,所以false的最大值为falsefalse
15.作用于同一点的三个力F1,F2,F3平衡.已知F1=4N,F2=5N,F1与F2之间的夹角是60°,则力F3的大小为______N.
【答案】false
【考点】正余弦定理在物理上的应用
【解析】由题意可知,三个力false平衡,则false与false的合力false与false等大反向,所以在false中,由余弦定理可得,false,即false
16.如图,在矩形ACD中,点E在边AD上,点F在边BC上,false,∠BFE=120°,EF=2.
若△CEF的面积为false,则AB=________,sin∠BEC=________.
【答案】false
【考点】双空题:正余弦定理在平面几何中的应用
【解析】由题意,因为false,所以false,则在false中,可得falsefalse,由false,可解得false,在false中,可得false,所以falsefalse又false,所以false,在false中,由余弦定理可得,false,解得falsefalse,在false中,由余弦定理可得,false
false,解得false,则在false中,falsefalse,则false
四?解答题(本大题共6小题,共70分.解答时应写出文字说明?证明过程或演算步骤)
17.(本小题满分10分)
(1)求false的值;
(2)求false的值.
【考点】平面向量的数量积的坐标运算?模的求解
【解析】
(1)由题意,因为false,所以false
所以false;
(2)由(1)知false,所以|2m+false,
所以|2m+false.
18.(本小题满分12分)
已知z是复数,false+3i为实数(i为虚数单位),且false.
(1)求z;
(2)若z和(z+mi)2在复平面内对应的点都在第一象限,求实数m的取值范围.
【考点】复数的运算?几何意义
【解析】(1)由题意可设false,则false,
又因为false为实数,所以false,
因为false,所以false,解得false,
所以false
(2)若false和false在复平面内对应的点都在第一象限,
则false,
所以有false,且false,解得一false,则实数false的取值范围为false
19.(本小题满分12分)
在①a=7;②csinA=4;③false这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,则求出该三角形面积;若问题中的三角形不存在,则请说明理由.
问题:是否存在锐角三角形ABC,它的内角A,B,C的对边分别为a,b,c,且c=8,false,__________?
【考点】结构不良题:解三角形与三角恒等变换综合应用
【解析】在false中,因为false,且false,
所以false,即false,
又因为false,所以false,所以false,
在false中,由false,可得false,
选①:由余弦定理可得false,即false,解得false或false,
所以false或103;
选②:false,故该三角形不存在;
选③:由false可得,false,
则由正弦定理可得,false,即false,
且false
所以false
20.(本小题满分12分)
设函数false.
(1)求f(x)的最小正周期;
(2)设方程false在区间false内的两解分别为x1,x2,求cos(x1-x2)的值.
【考点】三角函数的图像与性质?三角恒等变换给值求值问题
【解析】(1)由题意,false,
则false的最小正周期为false
(2)由(1)知false所以方程false可化为:false,
由false为方程false的两个根可得,false且false,
则在区间false内false,解得false,即false,
所以false
21.(本小题满分12分)
关于公式sin(α+β)=sinαcosβ+cosαsinβ的证明,前人做过许多探索.对于α,β均为锐角的情形,推导该公式常可以通过构造图形来完成.
(1)填空,完成推导过程(约定:只考虑α,β,α+β均为锐角的情形)
证明:构造一个矩形如图形1,在这个矩形GHMN中,点P在边MN上,点Q在边GN上,QT⊥HM,垂足为T,∠HPQ=90°,设HQ=1,∠QHP=α,∠PHM=β.
在直角三角形QHP中,QP=sinα,PH=cosα,
在直角三角形PHM中,PM=①,
在直角三角形QPN中,∠QPN=β,PN=sinαcosβ,
在直角三角形HQT中,QT=②,
因为QT=PM+PN,所以sin(α+β)=sinαcosβ+cosαsinβ.
(2)请你运用提供的图形和信息(见图形2)完成公式(约定:只考虑α,β均为锐角的情形)的推导.
【考点】开放性试题:两角和的正弦公式证明
【解析】(1)由题意可知,在直角三角形false中,false在直角三角形false中,falsefalse
(2)由题意可知,在false中,false,且false,
所以false,
在false中,false,所以false,
在false中,false,所以false,
又false,
所以false,
化简可得,false得证.
22.(本小题满分12分)
已知向量false为坐标原点.
(1)当false时,求false与false的夹角的余弦值;
(2)若false三点共线,求false的最小值.
【考点】平面向量数量积的坐标运算、平面向量共线的充要条件、基本不等式综合应用
【解析】(1)当false时false,
所以false
则false,
所以false;
(2)若false三点共线,则false,
又因为false,
则false,解得false,则false,
因为false,所以false,
所以false,
当且仅当false,即false时取等号,
所以false的最小值为false.
同课章节目录
