陕西省西安市西工大附属高中2021届高三下学期5月第十二次适应性考试数学试题 Word版含答案
文档属性
| 名称 | 陕西省西安市西工大附属高中2021届高三下学期5月第十二次适应性考试数学试题 Word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-17 00:00:00 | ||
图片预览




文档简介
西北工业大学附属中学高2021届第十二次适应性训练
理科数学
一?选择题
1. 已知集合,集合,则( )
A. B.
C. D.
2. 欧拉公式(i为虚数单位)是由瑞士著名的数学家欧拉发现的,它将指数函数的定义域扩大到复数集,建立了三角函数和指数函数的关系,它在复变函数论里非常重要,被誉为“数学中的天桥”.根据欧拉公式可知,表示的复数在复平面中对应的点位于( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
3. 一组数据的平均数为a,方差为b,将这组数据的每个数都乘以得到一组新数据,则下列说法正确的是( )
A. 这组新数据的平均数为a B. 这组新数据的平均数为
C. 这组新数据的方差为mb D. 这组新数据的方差为m2b
4. 《三十六计》是中华民族珍贵的文化遗产之一,是一部传习久远的兵法奇书,与《孙子兵法》合称我国古代兵法谋略学的双壁.三十六计共分胜战计?敌战计?攻战计?混战计?并战计?败战计六套,每一套都包含六计,合三十六个计策,如果从这36个计策中任取2个计策,则这2个计策都来自同一套的概率为( )
A. B. C. D.
5. 函数的部分图像是( )
A. B.
C. D.
6. 已知等差数列的前项和为,若,,,则n的值为( )
A. 60 B. 55 C. 50 D. 45
7. 过抛物线的焦点F的直线l交抛物线于A,B两点,且,则直线l的斜率是( )
A. B. C. D.
8. 直线交双曲线于P,Q两点,M是双曲线C上一点,若直线MP与直线MQ的斜率之积是,则双曲线C的离心率是( )
A. 2 B. C. D. 4
9. 己知四面体ABCD的每个顶点都在球O的表面上,,,底面ABC,M为的重心,且直线DM与底面ABC所成角的正切值为,则球O的表面积是( )
A. B. C. D.
10. 正的边长为3,M是正所在平面内一点,则最小值是( )
A. B. C. D.
11. 己知实数x,y满足条件,则的最大值是( )
A. 1 B. C. D. 3
12. 定义在上的函数满足,且,则不等式的解集为( )
A. B. C. D.
二?填空题
13. 二项式展开式中的常数项是___________
14. 直线被圆截得弦长的最小值是___________
15. 将函数的图像向左平移个单位长度,再把所得图像上所有点的横坐标伸长到原来的4倍(纵坐标保持不变)得到的图像,则的解析式为___________
16. 在直角坐标系中,定义两点与之间的“直角距离”为.若A,B是椭圆上任意两点,则的最大值是___________
三?解答题
17. 在中,内角A,B,C所对的边分别为a,b,c,.
(1)求的值;
(2)若且,求面积.
18. 已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.
(Ⅰ)证明:⊥平面;
(Ⅱ)求平面与平面所成角的余弦值;
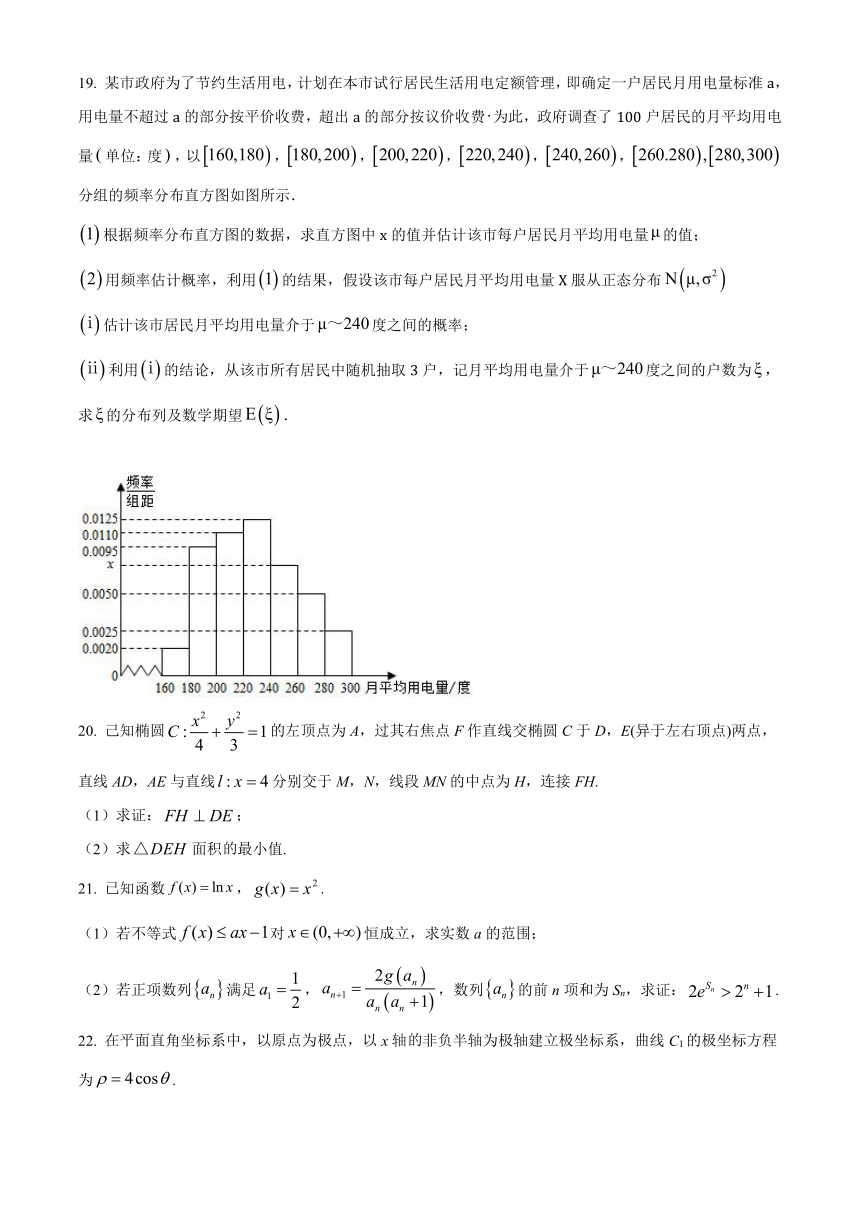
19. 某市政府为了节约生活用电,计划在本市试行居民生活用电定额管理,即确定一户居民月用电量标准a,用电量不超过a的部分按平价收费,超出a的部分按议价收费为此,政府调查了100户居民的月平均用电量单位:度,以,,,,,分组的频率分布直方图如图所示.
根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量的值;
用频率估计概率,利用的结果,假设该市每户居民月平均用电量X服从正态分布
估计该市居民月平均用电量介于度之间的概率;
利用的结论,从该市所有居民中随机抽取3户,记月平均用电量介于度之间的户数为,求的分布列及数学期望.
20. 己知椭圆的左顶点为A,过其右焦点F作直线交椭圆C于D,E(异于左右顶点)两点,直线AD,AE与直线分别交于M,N,线段MN的中点为H,连接FH.
(1)求证:;
(2)求面积最小值.
21. 已知函数,.
(1)若不等式对恒成立,求实数a的范围;
(2)若正项数列满足,,数列的前n项和为Sn,求证:.
22. 在平面直角坐标系中,以原点为极点,以x轴非负半轴为极轴建立极坐标系,曲线C1的极坐标方程为.
(1)若曲线的参数方程为(为参数),求曲线C1的直角坐标方程和曲线的普通方程;
(2)若曲线参数方程为(t为参数)点,曲线与曲线的交点分别为M,N,求的取值范围.
23. 已知函数.
(1)若,解不等式;
(2)若不等式对恒成立,求实数a的取值范围.
西北工业大学附属中学高2021届第十二次适应性训练
理科数学 答案版
一?选择题
1. 已知集合,集合,则( )
A. B.
C. D.
【答案】C
2. 欧拉公式(i为虚数单位)是由瑞士著名的数学家欧拉发现的,它将指数函数的定义域扩大到复数集,建立了三角函数和指数函数的关系,它在复变函数论里非常重要,被誉为“数学中的天桥”.根据欧拉公式可知,表示的复数在复平面中对应的点位于( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
【答案】D
3. 一组数据的平均数为a,方差为b,将这组数据的每个数都乘以得到一组新数据,则下列说法正确的是( )
A. 这组新数据的平均数为a B. 这组新数据的平均数为
C. 这组新数据的方差为mb D. 这组新数据的方差为m2b
【答案】D
4. 《三十六计》是中华民族珍贵的文化遗产之一,是一部传习久远的兵法奇书,与《孙子兵法》合称我国古代兵法谋略学的双壁.三十六计共分胜战计?敌战计?攻战计?混战计?并战计?败战计六套,每一套都包含六计,合三十六个计策,如果从这36个计策中任取2个计策,则这2个计策都来自同一套的概率为( )
A. B. C. D.
【答案】C
5. 函数的部分图像是( )
A. B.
C. D.
【答案】A
6. 已知等差数列的前项和为,若,,,则n的值为( )
A. 60 B. 55 C. 50 D. 45
【答案】C
7. 过抛物线的焦点F的直线l交抛物线于A,B两点,且,则直线l的斜率是( )
A. B. C. D.
【答案】D
8. 直线交双曲线于P,Q两点,M是双曲线C上一点,若直线MP与直线MQ的斜率之积是,则双曲线C的离心率是( )
A. 2 B. C. D. 4
【答案】A
9. 己知四面体ABCD的每个顶点都在球O的表面上,,,底面ABC,M为的重心,且直线DM与底面ABC所成角的正切值为,则球O的表面积是( )
A. B. C. D.
【答案】B
10. 正的边长为3,M是正所在平面内一点,则最小值是( )
A. B. C. D.
【答案】C
11. 己知实数x,y满足条件,则的最大值是( )
A. 1 B. C. D. 3
【答案】C
12. 定义在上的函数满足,且,则不等式的解集为( )
A. B. C. D.
【答案】B
二?填空题
13. 二项式展开式中的常数项是___________
【答案】
14. 直线被圆截得弦长的最小值是___________
【答案】
15. 将函数的图像向左平移个单位长度,再把所得图像上所有点的横坐标伸长到原来的4倍(纵坐标保持不变)得到的图像,则的解析式为___________
【答案】
16. 在直角坐标系中,定义两点与之间的“直角距离”为.若A,B是椭圆上任意两点,则的最大值是___________
【答案】
三?解答题
17. 在中,内角A,B,C所对的边分别为a,b,c,.
(1)求的值;
(2)若且,求面积.
【答案】(1);(2).
18. 已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.
(Ⅰ)证明:⊥平面;
(Ⅱ)求平面与平面所成角的余弦值;
【答案】(Ⅰ)证明见解析;(Ⅱ).
19. 某市政府为了节约生活用电,计划在本市试行居民生活用电定额管理,即确定一户居民月用电量标准a,用电量不超过a的部分按平价收费,超出a的部分按议价收费为此,政府调查了100户居民的月平均用电量单位:度,以,,,,,分组的频率分布直方图如图所示.
根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量的值;
用频率估计概率,利用的结果,假设该市每户居民月平均用电量X服从正态分布
估计该市居民月平均用电量介于度之间的概率;
利用的结论,从该市所有居民中随机抽取3户,记月平均用电量介于度之间的户数为,求的分布列及数学期望.
【答案】(1)225.6.
(2) (i) ;(ii) 分布列见解析;
20. 己知椭圆的左顶点为A,过其右焦点F作直线交椭圆C于D,E(异于左右顶点)两点,直线AD,AE与直线分别交于M,N,线段MN的中点为H,连接FH.
(1)求证:;
(2)求面积最小值.
【答案】(1)证明见解析;(2).
21. 已知函数,.
(1)若不等式对恒成立,求实数a的范围;
(2)若正项数列满足,,数列的前n项和为Sn,求证:.
【答案】(1);(2)证明见解析.
22. 在平面直角坐标系中,以原点为极点,以x轴非负半轴为极轴建立极坐标系,曲线C1的极坐标方程为.
(1)若曲线的参数方程为(为参数),求曲线C1的直角坐标方程和曲线的普通方程;
(2)若曲线参数方程为(t为参数)点,曲线与曲线的交点分别为M,N,求的取值范围.
【答案】(1)的直角坐标方程为:,的普通方程为;(2).
23. 已知函数.
(1)若,解不等式;
(2)若不等式对恒成立,求实数a的取值范围.
【答案】(1);(2).
理科数学
一?选择题
1. 已知集合,集合,则( )
A. B.
C. D.
2. 欧拉公式(i为虚数单位)是由瑞士著名的数学家欧拉发现的,它将指数函数的定义域扩大到复数集,建立了三角函数和指数函数的关系,它在复变函数论里非常重要,被誉为“数学中的天桥”.根据欧拉公式可知,表示的复数在复平面中对应的点位于( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
3. 一组数据的平均数为a,方差为b,将这组数据的每个数都乘以得到一组新数据,则下列说法正确的是( )
A. 这组新数据的平均数为a B. 这组新数据的平均数为
C. 这组新数据的方差为mb D. 这组新数据的方差为m2b
4. 《三十六计》是中华民族珍贵的文化遗产之一,是一部传习久远的兵法奇书,与《孙子兵法》合称我国古代兵法谋略学的双壁.三十六计共分胜战计?敌战计?攻战计?混战计?并战计?败战计六套,每一套都包含六计,合三十六个计策,如果从这36个计策中任取2个计策,则这2个计策都来自同一套的概率为( )
A. B. C. D.
5. 函数的部分图像是( )
A. B.
C. D.
6. 已知等差数列的前项和为,若,,,则n的值为( )
A. 60 B. 55 C. 50 D. 45
7. 过抛物线的焦点F的直线l交抛物线于A,B两点,且,则直线l的斜率是( )
A. B. C. D.
8. 直线交双曲线于P,Q两点,M是双曲线C上一点,若直线MP与直线MQ的斜率之积是,则双曲线C的离心率是( )
A. 2 B. C. D. 4
9. 己知四面体ABCD的每个顶点都在球O的表面上,,,底面ABC,M为的重心,且直线DM与底面ABC所成角的正切值为,则球O的表面积是( )
A. B. C. D.
10. 正的边长为3,M是正所在平面内一点,则最小值是( )
A. B. C. D.
11. 己知实数x,y满足条件,则的最大值是( )
A. 1 B. C. D. 3
12. 定义在上的函数满足,且,则不等式的解集为( )
A. B. C. D.
二?填空题
13. 二项式展开式中的常数项是___________
14. 直线被圆截得弦长的最小值是___________
15. 将函数的图像向左平移个单位长度,再把所得图像上所有点的横坐标伸长到原来的4倍(纵坐标保持不变)得到的图像,则的解析式为___________
16. 在直角坐标系中,定义两点与之间的“直角距离”为.若A,B是椭圆上任意两点,则的最大值是___________
三?解答题
17. 在中,内角A,B,C所对的边分别为a,b,c,.
(1)求的值;
(2)若且,求面积.
18. 已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.
(Ⅰ)证明:⊥平面;
(Ⅱ)求平面与平面所成角的余弦值;
19. 某市政府为了节约生活用电,计划在本市试行居民生活用电定额管理,即确定一户居民月用电量标准a,用电量不超过a的部分按平价收费,超出a的部分按议价收费为此,政府调查了100户居民的月平均用电量单位:度,以,,,,,分组的频率分布直方图如图所示.
根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量的值;
用频率估计概率,利用的结果,假设该市每户居民月平均用电量X服从正态分布
估计该市居民月平均用电量介于度之间的概率;
利用的结论,从该市所有居民中随机抽取3户,记月平均用电量介于度之间的户数为,求的分布列及数学期望.
20. 己知椭圆的左顶点为A,过其右焦点F作直线交椭圆C于D,E(异于左右顶点)两点,直线AD,AE与直线分别交于M,N,线段MN的中点为H,连接FH.
(1)求证:;
(2)求面积最小值.
21. 已知函数,.
(1)若不等式对恒成立,求实数a的范围;
(2)若正项数列满足,,数列的前n项和为Sn,求证:.
22. 在平面直角坐标系中,以原点为极点,以x轴非负半轴为极轴建立极坐标系,曲线C1的极坐标方程为.
(1)若曲线的参数方程为(为参数),求曲线C1的直角坐标方程和曲线的普通方程;
(2)若曲线参数方程为(t为参数)点,曲线与曲线的交点分别为M,N,求的取值范围.
23. 已知函数.
(1)若,解不等式;
(2)若不等式对恒成立,求实数a的取值范围.
西北工业大学附属中学高2021届第十二次适应性训练
理科数学 答案版
一?选择题
1. 已知集合,集合,则( )
A. B.
C. D.
【答案】C
2. 欧拉公式(i为虚数单位)是由瑞士著名的数学家欧拉发现的,它将指数函数的定义域扩大到复数集,建立了三角函数和指数函数的关系,它在复变函数论里非常重要,被誉为“数学中的天桥”.根据欧拉公式可知,表示的复数在复平面中对应的点位于( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
【答案】D
3. 一组数据的平均数为a,方差为b,将这组数据的每个数都乘以得到一组新数据,则下列说法正确的是( )
A. 这组新数据的平均数为a B. 这组新数据的平均数为
C. 这组新数据的方差为mb D. 这组新数据的方差为m2b
【答案】D
4. 《三十六计》是中华民族珍贵的文化遗产之一,是一部传习久远的兵法奇书,与《孙子兵法》合称我国古代兵法谋略学的双壁.三十六计共分胜战计?敌战计?攻战计?混战计?并战计?败战计六套,每一套都包含六计,合三十六个计策,如果从这36个计策中任取2个计策,则这2个计策都来自同一套的概率为( )
A. B. C. D.
【答案】C
5. 函数的部分图像是( )
A. B.
C. D.
【答案】A
6. 已知等差数列的前项和为,若,,,则n的值为( )
A. 60 B. 55 C. 50 D. 45
【答案】C
7. 过抛物线的焦点F的直线l交抛物线于A,B两点,且,则直线l的斜率是( )
A. B. C. D.
【答案】D
8. 直线交双曲线于P,Q两点,M是双曲线C上一点,若直线MP与直线MQ的斜率之积是,则双曲线C的离心率是( )
A. 2 B. C. D. 4
【答案】A
9. 己知四面体ABCD的每个顶点都在球O的表面上,,,底面ABC,M为的重心,且直线DM与底面ABC所成角的正切值为,则球O的表面积是( )
A. B. C. D.
【答案】B
10. 正的边长为3,M是正所在平面内一点,则最小值是( )
A. B. C. D.
【答案】C
11. 己知实数x,y满足条件,则的最大值是( )
A. 1 B. C. D. 3
【答案】C
12. 定义在上的函数满足,且,则不等式的解集为( )
A. B. C. D.
【答案】B
二?填空题
13. 二项式展开式中的常数项是___________
【答案】
14. 直线被圆截得弦长的最小值是___________
【答案】
15. 将函数的图像向左平移个单位长度,再把所得图像上所有点的横坐标伸长到原来的4倍(纵坐标保持不变)得到的图像,则的解析式为___________
【答案】
16. 在直角坐标系中,定义两点与之间的“直角距离”为.若A,B是椭圆上任意两点,则的最大值是___________
【答案】
三?解答题
17. 在中,内角A,B,C所对的边分别为a,b,c,.
(1)求的值;
(2)若且,求面积.
【答案】(1);(2).
18. 已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.
(Ⅰ)证明:⊥平面;
(Ⅱ)求平面与平面所成角的余弦值;
【答案】(Ⅰ)证明见解析;(Ⅱ).
19. 某市政府为了节约生活用电,计划在本市试行居民生活用电定额管理,即确定一户居民月用电量标准a,用电量不超过a的部分按平价收费,超出a的部分按议价收费为此,政府调查了100户居民的月平均用电量单位:度,以,,,,,分组的频率分布直方图如图所示.
根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量的值;
用频率估计概率,利用的结果,假设该市每户居民月平均用电量X服从正态分布
估计该市居民月平均用电量介于度之间的概率;
利用的结论,从该市所有居民中随机抽取3户,记月平均用电量介于度之间的户数为,求的分布列及数学期望.
【答案】(1)225.6.
(2) (i) ;(ii) 分布列见解析;
20. 己知椭圆的左顶点为A,过其右焦点F作直线交椭圆C于D,E(异于左右顶点)两点,直线AD,AE与直线分别交于M,N,线段MN的中点为H,连接FH.
(1)求证:;
(2)求面积最小值.
【答案】(1)证明见解析;(2).
21. 已知函数,.
(1)若不等式对恒成立,求实数a的范围;
(2)若正项数列满足,,数列的前n项和为Sn,求证:.
【答案】(1);(2)证明见解析.
22. 在平面直角坐标系中,以原点为极点,以x轴非负半轴为极轴建立极坐标系,曲线C1的极坐标方程为.
(1)若曲线的参数方程为(为参数),求曲线C1的直角坐标方程和曲线的普通方程;
(2)若曲线参数方程为(t为参数)点,曲线与曲线的交点分别为M,N,求的取值范围.
【答案】(1)的直角坐标方程为:,的普通方程为;(2).
23. 已知函数.
(1)若,解不等式;
(2)若不等式对恒成立,求实数a的取值范围.
【答案】(1);(2).
同课章节目录
