垂径定理

(共11张PPT)
实践探究
　把一个圆沿着它的任意一条直径对折，重复几次，你发现了什么？由此你能得到什么结论？
可以发现：
圆是轴对称图形，任何一条直径所在直线都是它的对称轴．　
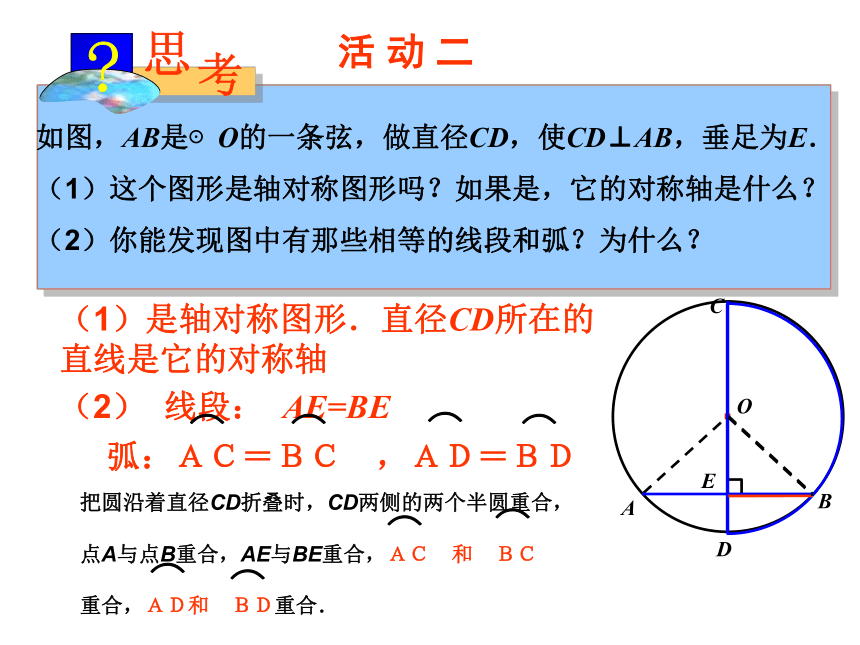
如图，AB是⊙O的一条弦，做直径CD，使CD⊥AB，垂足为E．
（1）这个图形是轴对称图形吗？如果是，它的对称轴是什么？
（2）你能发现图中有那些相等的线段和弧？为什么？
·
O
A
B
C
D
E
活 动 二
（1）是轴对称图形．直径CD所在的直线是它的对称轴
（2） 线段： AE=BE
⌒
⌒
弧：ＡＣ＝ＢＣ　，ＡＤ＝ＢＤ
⌒
⌒
把圆沿着直径CD折叠时，CD两侧的两个半圆重合，　
点A与点B重合，AE与BE重合，ＡＣ　和　ＢＣ　
重合，ＡＤ和　ＢＤ重合．
⌒
⌒
⌒
⌒
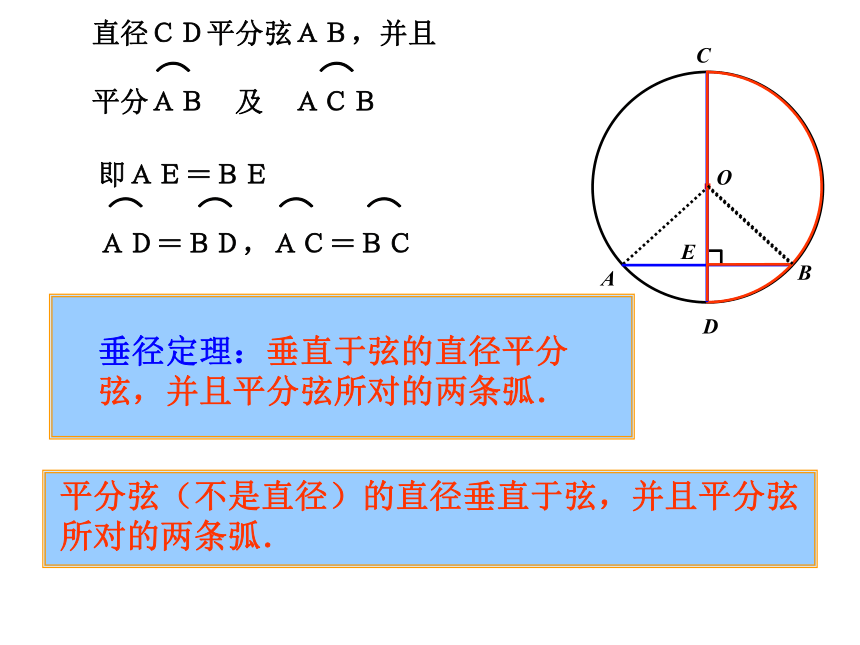
直径ＣＤ平分弦ＡＢ，并且
平分ＡＢ　及　ＡＣＢ
⌒
⌒
·
O
A
B
C
D
E
垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧．
平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．
即ＡＥ＝ＢＥ　
ＡＤ＝ＢＤ，ＡＣ＝ＢＣ
⌒
⌒
⌒
⌒
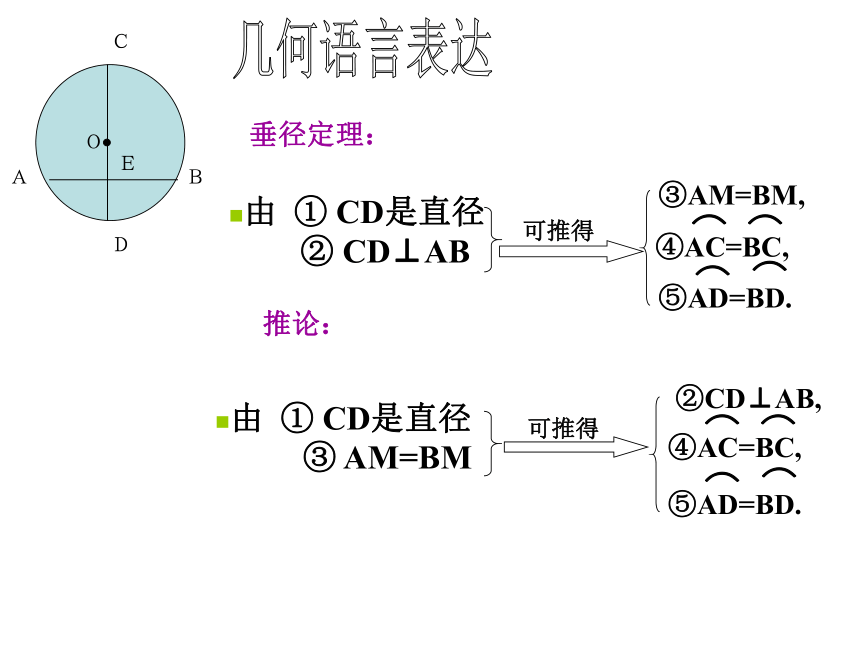
③AM=BM,
由 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
⑤AD=BD.
⌒
⌒
④AC=BC,
②CD⊥AB,
由 ① CD是直径
③ AM=BM
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
可推得
Ｄ
Ｃ
Ａ
Ｂ
Ｅ
Ｏ
垂径定理：
推论：
判断下列说法的正误
①平分弧的直径必平分弧所对的弦
　②平分弦的直线必垂直弦
③垂直于弦的直径平分这条弦
④平分弦的直径垂直于这条弦
⑤弦的垂直平分线是圆的直径
⑥平分弦所对的一条弧的直径必垂直这条弦
⑦在圆中，如果一条直线经过圆心且平分弦，　
　必平分此弦所对的弧
1．如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，求⊙O的半径．
·
O
A
B
E
练习
解：
答：⊙O的半径为5cm.
活 动 三
在Rt △ AOE 中
2．如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB于D，OE⊥AC于E，求证四边形ADOE是正方形．
D
·
O
A
B
C
E
证明：
∴四边形ADOE为矩形，
又　∵AC=AB
∴ AE=AD
∴ 四边形ADOE为正方形.
例2：已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点。
求证：AC＝BD。
证明：过O作OE⊥AB，垂足为E，
则AE＝BE，CE＝DE。
AE－CE＝BE－DE。
所以，AC＝BD
E
.
A
C
D
B
O
某地有一座圆弧形拱桥圆心为Ｏ，桥下水面宽度为７、2 m ，过O 作OC ⊥ AB 于D， 交圆弧于C，CD=2、4m， 现有一艘宽3m，船舱顶部为方形并高出水面（AB）2m的货船要经过拱桥，此货船能否顺利通过这座拱桥？
C
N
M
A
E
H
F
B
D
O
结束寄语
不学自知,不问自晓,古今行事,未之有也.
下课了!