2020-2021学年八年级数学人教版下册第18章平行四边形章末练习(word版含答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册第18章平行四边形章末练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-16 12:12:32 | ||
图片预览

文档简介
第18章《平行四边形》章末练习
一、单选题
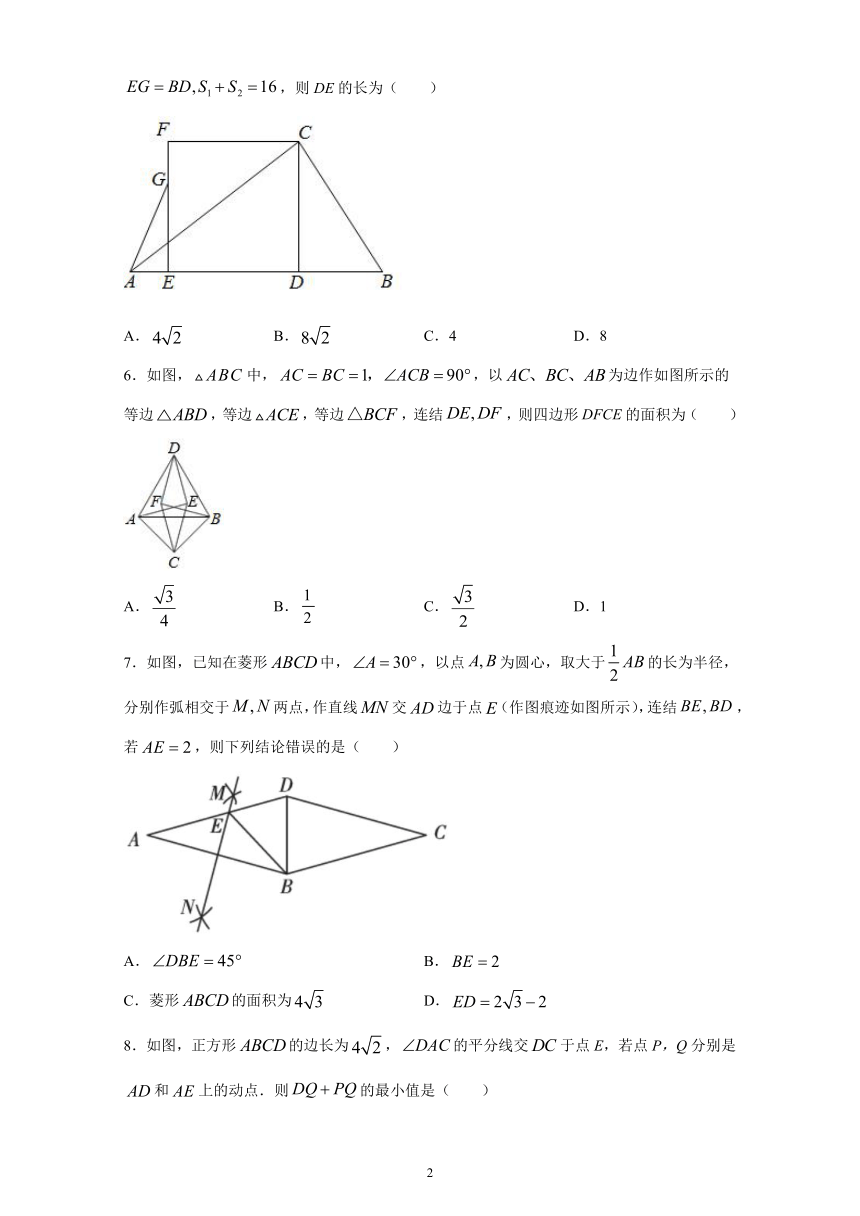
1.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6cm,BC=8cm.则EF的长是(
)
A.2.2cm
B.2.3cm
C.2.4cm
D.2.5cm
2.如图,RtABC≌RtDCB,其中∠ABC=90°,AB=3,BC=4,O为BC中点,EF过点交AC、BD于点E、F,连接BE、CF,则下列结论错误(
)
A.四边形BECF为平行四边形
B.当BF=3.5时,
四边形BECF为矩形
C.当BF=2.5时,四边形BECF为菱形
D.四边形BECF不可能为正方形
3.如图,在菱形中,标出了四条线段的长度,其中有一个长度是标错的,这个长度是(
)
A.2
B.3
C.4
D.5
4.如图,在平行四边形中,,平分交于点,若,则的度数是(
)
A.10°
B.15°
C.20°
D.25°
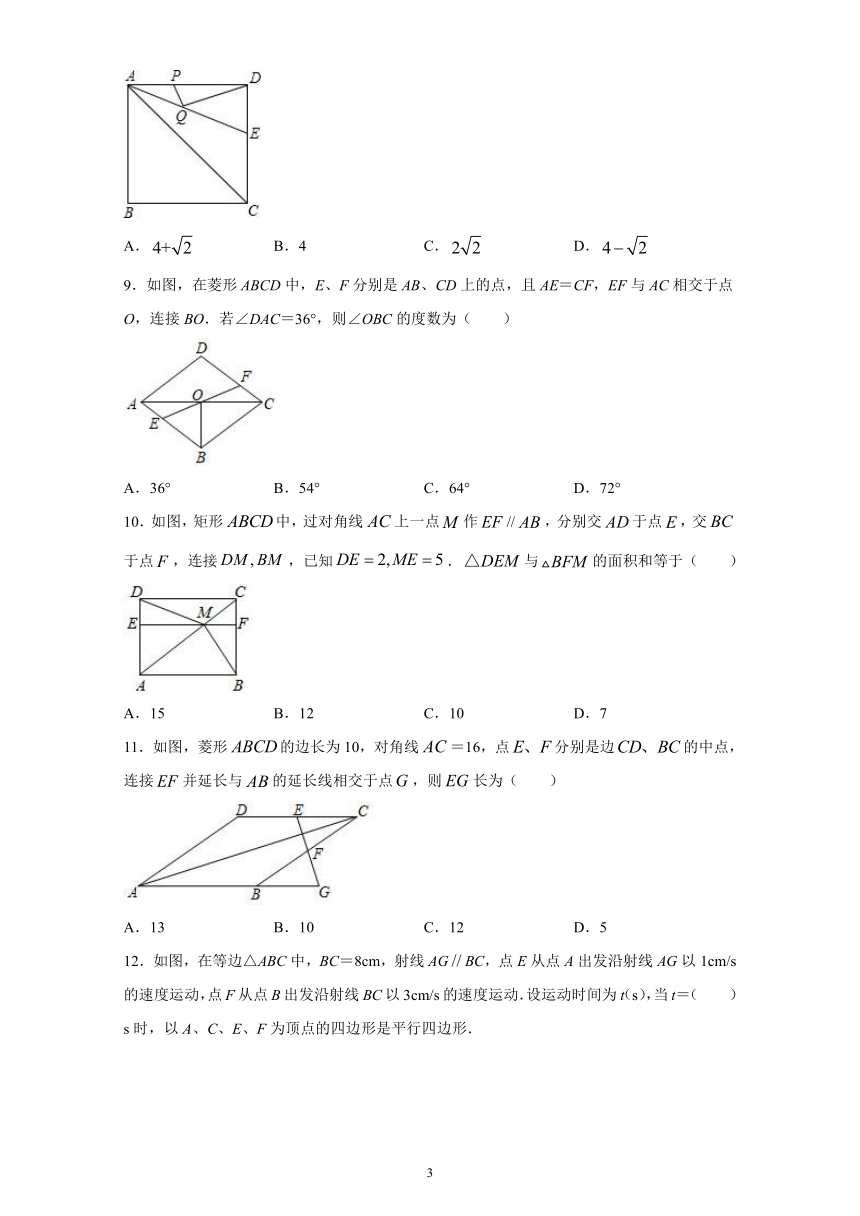
5.如图,在中,于点D,正方形CDEF的顶点E在线段AD上,G是边EF上一点,连结AG,记面积为,面积为,若,则DE的长为(
)
A.
B.
C.4
D.8
6.如图,中,,以为边作如图所示的等边,等边,等边,连结,则四边形的面积为(
)
A.
B.
C.
D.1
7.如图,已知在菱形中,,以点为圆心,取大于的长为半径,分别作弧相交于两点,作直线交边于点(作图痕迹如图所示),连结,若,则下列结论错误的是(
)
A.
B.
C.菱形的面积为
D.
8.如图,正方形的边长为,的平分线交于点E,若点P,Q分别是和上的动点.则的最小值是(
)
A.
B.4
C.
D.
9.如图,在菱形ABCD中,E、F分别是AB、CD上的点,且AE=CF,EF与AC相交于点O,连接BO.若∠DAC=36°,则∠OBC的度数为(
)
A.36°
B.54°
C.64°
D.72°
10.如图,矩形中,过对角线上一点作//,分别交于点,交于点,连接,已知.与的面积和等于(
)
A.15
B.12
C.10
D.7
11.如图,菱形的边长为10,对角线=16,点分别是边的中点,连接并延长与的延长线相交于点,则长为(
)
A.13
B.10
C.12
D.5
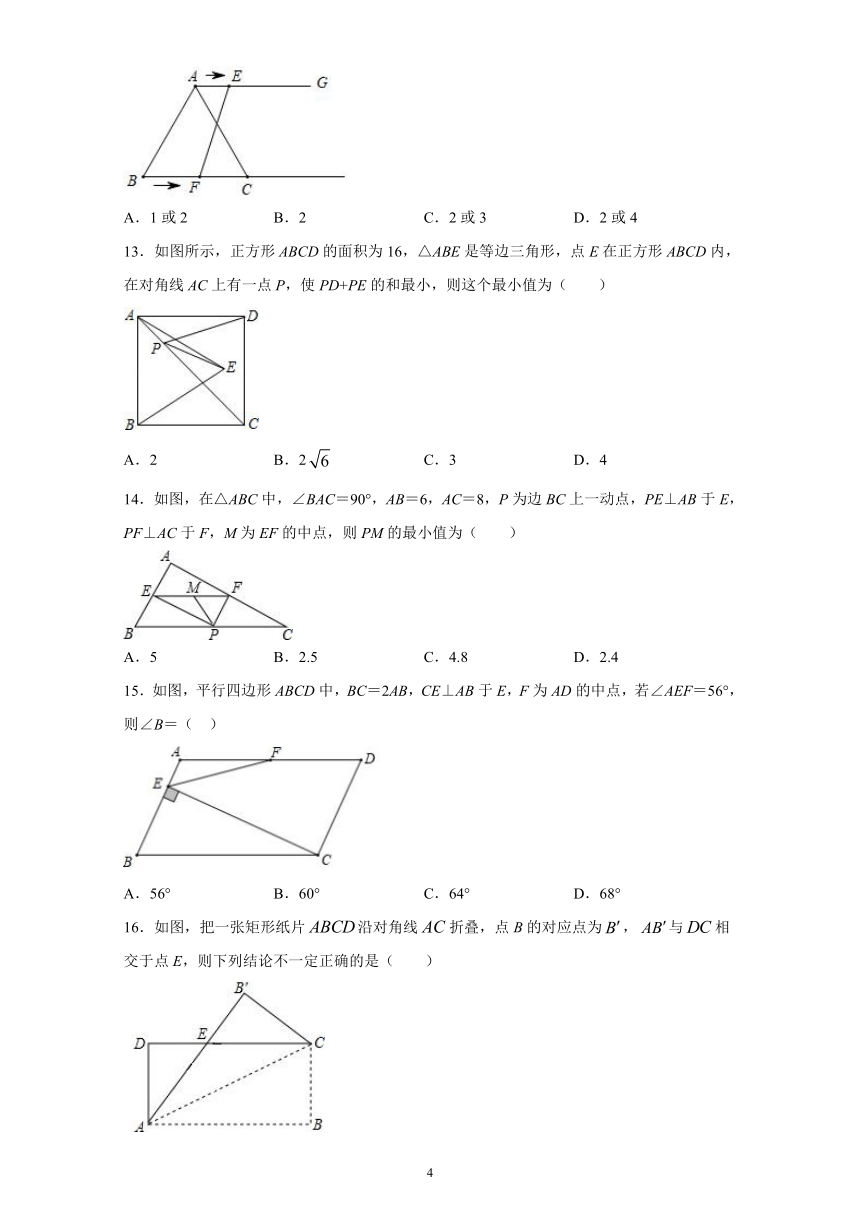
12.如图,在等边△ABC中,BC=8cm,射线AGBC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以3cm/s的速度运动.设运动时间为t(s),当t=( )s时,以A、C、E、F为顶点的四边形是平行四边形.
A.1或2
B.2
C.2或3
D.2或4
13.如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A.2
B.2
C.3
D.4
14.如图,在△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
A.5
B.2.5
C.4.8
D.2.4
15.如图,平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=56°,则∠B=(
)
A.56°
B.60°
C.64°
D.68°
16.如图,把一张矩形纸片沿对角线折叠,点B的对应点为,与相交于点E,则下列结论不一定正确的是(
)
A.
B.
C.
D.
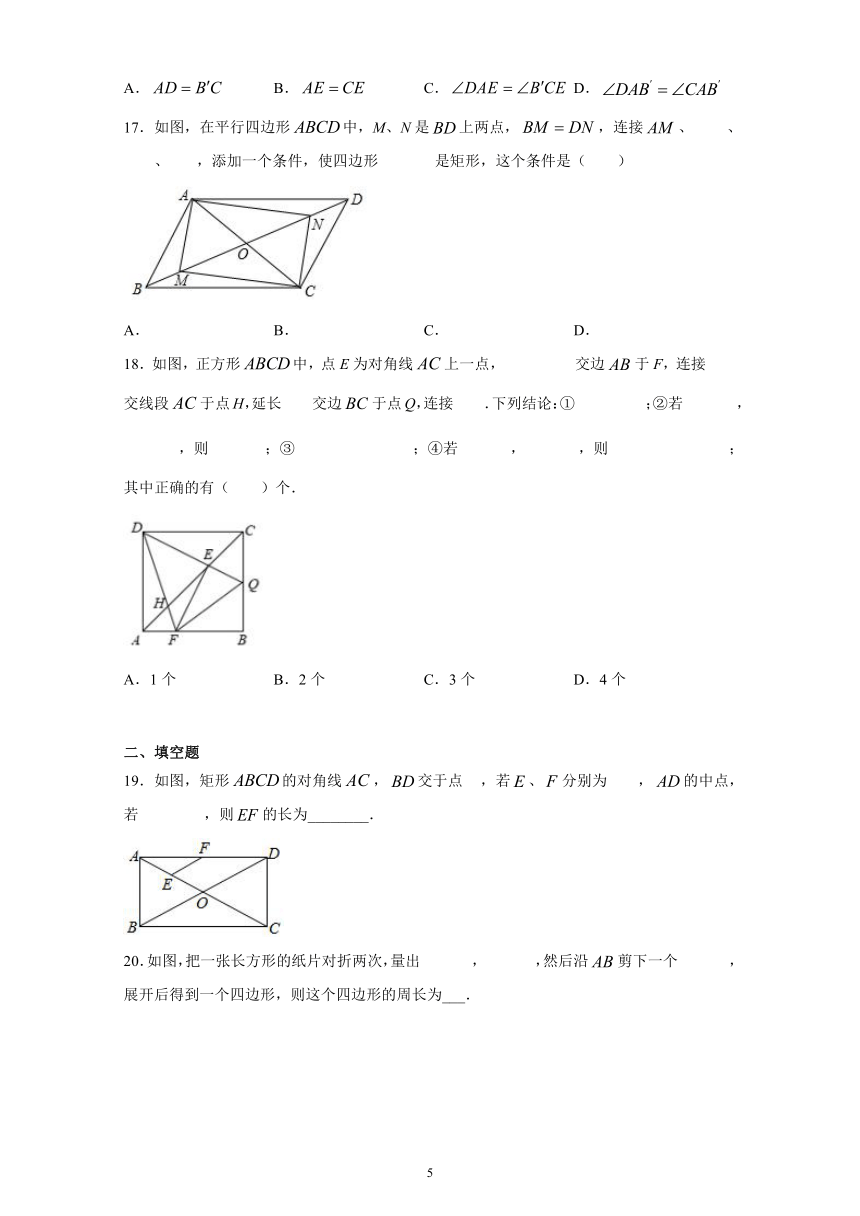
17.如图,在平行四边形中,M、N是上两点,,连接、、、,添加一个条件,使四边形是矩形,这个条件是(
)
A.
B.
C.
D.
18.如图,正方形中,点E为对角线上一点,交边于F,连接交线段于点H,延长交边于点Q,连接.下列结论:①;②若,,则;③;④若,,则;其中正确的有(
)个.
A.1个
B.2个
C.3个
D.4个
二、填空题
19.如图,矩形的对角线,交于点,若、分别为,的中点,若,则的长为________.
20.如图,把一张长方形的纸片对折两次,量出,,然后沿剪下一个,展开后得到一个四边形,则这个四边形的周长为___.
21.如图,四边形ABCD是正方形,△CBE是等边三角形,则∠AEB=__.
22.如图a是长方形纸带,∠DEF=22°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是________°.
23.如图,在中,按以下步骤作图:①以点A为圆心,的长为半径画弧,交于点F;②分别以点F,B为圆心,以大于的长为半径画弧,两弧在内交于点G;③作射线,交边于点E,交于点O,连接.若,,则四边形的面积为_________.
三、解答题
24.如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求DF的长.
25.如图,等边△AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
26.如图,在平行四边形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,AE=CG,AH=CF,且EG平分∠HEF.
(1)求证:四边形EFGH是菱形;
(2)若EF=4,∠HEF=60°,求EG的长.
27.如图,已知在△ABC中AB=AC,AD是BC边上的中线,E,G分别是AC,DC的中点,F为DE延长线上的点,∠FCA=∠CEG.
(1)求证:AD∥CF;
(2)求证:四边形ADCF是矩形.
28.如图1,在菱形中,,,点为上一动点,在点的运动过程中,始终保持,,连接,,与相交于点.
(1)如图1,求证四边形为平行四边形;
(2)当点运动到什么位置时,四边形为矩形?并说明理由;
(3)如图2,延长到,使,连接,判断与的数量关系,并说明理由.
参考答案
1.D
解:∵四边形ABCD是矩形,
∴∠ABC=90°,BD=AC,BO=OD,
∵AB=6cm,BC=8cm,
∴由勾股定理得:AC===10(cm),
∴BD=10cm,DO=5cm,
∵点E、F分别是AO、AD的中点,
∴EF是△AOD的中位线,
∴EF=OD=2.5cm,
2.B
证明:∵RtABC≌RtDCB,
∴∠ACB=∠CBD,
∴BD∥AC,
∵O为BC中点,
∴OB=OC,
∵∠BOF=∠COE,
∴△BOF≌△COE,
∴BF=CE,
∴四边形BECF为平行四边形,故A选项正确;
∵∠ABC=90°,AB=3,BC=4,
∴AC=5,
∵BF=3.5,
∴CE=BF=3.5,AE=1.5,
∵,
∴∠BEC不是直角,故四边形BECF不为矩形,故B选项错误;
当BF=2.5时,则CE=BF=2.5,
∴AE=2.5,
∴AE=CE,
∴,
∴四边形BECF为菱形,故C选项正确;
∵AB=3,BC=4,AC=5,
∴,
∴四边形BECF不可能为正方形,故D选项正确;
3.A
解:∵四边形是菱形,
∴∠DOC=90°,AB=CD=5,
∵,
∴3、4、5没标错,
∵OA=OC=3,
∴2标错了,
4.C
解:∵平行四边形
∴AD∥BC,AB=DC,∠B=∠ADC
∴∠AEB=∠DAE
∵平分
∴∠BAE=∠DAE
∴∠BAE=∠AEB
∵
∴△BAE是等边三角形
∴∠BAE=∠DAE
=,AB=AE=BE
∴AE=DC,∠ADC=∠DAE
∵AD=AD
∴△EAD≌△CDA
∴∠DAC=∠ADE
∵AD∥BC
∴∠DAC=∠ACE=∠ADE=∠DAC
∵
∴∠DAC=∠ACE=∠ADE=∠DAC=40°
∴=120?
∴=180???∠ACE=20?
5.A
解:,
,
,
,
,
,
,
,
,
四边形是正方形,
,,
,
,
,
,
,
,
,
,
,
,
,
,
.
6.B
解:如图,过点作于,设与于,
,,
,,
以、、为边作如图所示的等边,等边,等边,
,,,
,
,,
,
,
,
,
,
,
在和中,
,
,
,
同理可求,
,
四边形是菱形,
,,
,
,
四边形的面积,
7.C
解:由作法知,MN是线段AB的垂直平分线
∴BE=AE=2
故选项B正确
∵BE=AE,∠A=30゜
∴∠EBA=∠A=30゜
∵四边形ABCD是菱形
∴AB=AD
∴∠ABD=∠ADB=(180゜?∠A)=75゜
∴∠DBE=∠ABD?∠EBA=45゜
故选项A正确
设MN交AB于点F,如图
∵MN⊥AB,∠A=30゜
∴EF=AE=1
由勾股定理得:
∴AD=AB=2AF=
∴ED=AD?AE==?2
故选项D正确
如图,过点D作DG⊥AB于点G
在Rt△ADG中,∠A=30゜,则
∴
从而选项C错误
8.B
解:作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,
∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=,
∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=32,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=32,
∴P′D′=4,即DQ+PQ的最小值为4,
9.B
解:∵四边形ABCD是菱形,
∴AB=BC=AD=CD,AB∥CD,AD∥BC,
∴∠EAO=∠FCO,∠DAC=∠ACB=36°,
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴AO=CO,
又∵AB=BC,
∴BO⊥AC,
∴∠OBC=90°﹣∠ACB=54°,
10.C
解:作PM⊥AB于P,交DC于Q.
则有四边形DEMQ,四边形QMFC,四边形AEMP,四边形MPBF都是矩形,
∴S△DEM=S△DQM,S△QCM=S△MFC,S△AEM=S△APM,S△MPB=S△MFB,S△ABC=S△ADC,
∴S△ABC-S△AMP-S△MCF=S△ADC-S△AEM-S△MQC,
∴S四边形DEMQ=S四边形MPBF,
∵DE=CF=2,
∴S△DEM=S△MFB=×2×5=5,
∴S△DEM+S△MFB=5+5=10,
11.C
解:连接BD,交AC于点O,如图:
∵菱形ABCD的边长为10,点E、F分别是边CD、BC的中点,
∴AB∥CD,AB=BC=CD=DA=10,EF∥BD,
∵AC、BD是菱形的对角线,AC=16,
∴AC⊥BD,AO=CO=8,OB=OD,
又∵AB∥CD,EF∥BD,
∴DE∥BG,BD∥EG,
∴四边形BDEG是平行四边形,
∴BD=EG,
在△COD中,∵OC⊥OD,CD=10,CO=8,
∴OB=OD=,
∴BD=2OD=12,
∴EG=BD=12;
12.D
解:当点F在C的左侧时,根据题意得:AE=tcm,BF=3tcm,
则CF=BC﹣BF=(8﹣3t)cm,
∵AG∥BC,
∴当AE=CF时,四边形AECF是平行四边形,
即t=8﹣3t,
解得:t=2;
当点F在C的右侧时,根据题意得:AE=tcm,BF=3tcm,
则CF=BF﹣BC=(3t﹣8)cm,
∵AG∥BC,
∴当AE=CF时,四边形AEFC是平行四边形,
即t=3t﹣8,
解得:t=4;
综上可得:当t=2或4s时,以A、C、E、F为顶点四边形是平行四边形,
13.D
解:设BE与AC交于点P',连接BD.
∵点B与D关于AC对称,
∴P'D=P'B,
∴P'D+P'E=P'B+P'E=BE最小.
∵正方形ABCD的面积为16,
∴AB=4,
又∵△ABE是等边三角形,
∴BE=AB=4.
14.D
解:连接AP,如图所示:
∵∠BAC=90°,AB=6,AC=8,
∴BC==10,
∵PE⊥AB,PF⊥AC,
∴四边形AFPE是矩形,
∴EF=AP,EF与AP互相平分,
∵M是EF的中点,
∴M为AP的中点,
∴PM=AP,
根据直线外一点到直线上任一点的距离,垂线段最短,
即AP⊥BC时,AP最短,同样PM也最短,
∴当AP⊥BC时,AP==4.8,
∴AP最短时,AP=4.8,
∴当PM最短时,PM=AP=2.4.
15.D
解:取BC的中点G,连接EG、FG,
∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∵CE⊥AB,
∴∠CEB=90°,
∴EG=BG=CG,
∴∠B=∠GEB,
∵BC=2AB,
∴EG=AB=CD,
∴∠EFG=∠FEG,
∵F点为AD的中点,G为BC的中点,
∴FG∥AB,
∴∠AEF=∠EFG=56°,
∴∠FEG=56°,
∴∠GEB=180°-56°-56°=68°,
∴∠B=68°.
16.D
解:∵四边形ABCD是矩形,
∴,CD∥AB,AD∥BC,
∴,,
由折叠性质得:,,,
∴,,
∴,,
,即,
故选项A、B、C正确,选项D错误,
17.D
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD
∵对角线BD上的两点M、N满足BM=DN,
∴OB-BM=OD-DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵2OM=AC,
∴MN=AC,
∴四边形AMCN是矩形.
18.D
解:如图,连接BE,
∵四边形ABCD为正方形,
∴CB=CD,∠BCE=∠DCE=45°,
在△BEC和△DEC中,
,
∴△DCE≌△BCE(SAS),
∴DE=BE,∠CDE=∠CBE,
∴∠ADE=∠ABE,
∵∠DAB=90°,∠DEF=90°,
∴∠ADE+∠AFE=180°,
∵∠AFE+∠EFB=180°,
∴∠ADE=∠EFB,
∴∠ABE=∠EFB,
∴EF=BE,
∴DE=EF,故①正确;
∵∠DEF=90°,DE=EF,
∴∠EDF=∠DFE=45°,
如图:延长BC到G,使CG=AF,连接DG,
在△ADF和△CDG中,
,
∴△ADF≌△CDG(SAS),
∴∠AFD=∠G,∠ADF=∠CDG,DF=DG,
∵∠ADF+∠CDQ=90°?∠FDQ=45°,
∴∠CDG+∠CDQ=45°=∠GDQ,
∴∠GDQ=∠FDQ,
又∵DG=DF,DQ=DQ,
∴△QDF≌△QDG(SAS),
∴FQ=QG,∠G=∠DFQ,
∴∠DFA=∠DFQ,故③正确;
∵AB=6,CQ=3,
∴BQ=3,FB=6?AF,FQ=QG=3+AF,
∵FQ2=FB2+BQ2,
∴(3+AF)2=9+(6?AF)2,
∴AF=2,故②正确;
如图:将△CDE绕点A顺时针旋转90°得到△ADM,连接MH,
∴△CDE≌△ADM,
∴AM=CE=4,∠DCE=∠DAM=45°,∠ADM=∠CDE,DM=DE,
∴∠MAH=90°,∠ADM+∠ADH=∠CDE+∠ADH=45°=∠MDH,
又∵DH=DH,
∴△DMH≌△DEH(SAS),
∴EH=MH,
∵MH==,
∴EH=MH=,
∴AC=AH+EH+EC=6+
∴AB=AC÷=,故④正确;
19.6
解:∵四边形是矩形,,
∴,,
∵、分别为,的中点,
∴;
20.4
解:由题意,四边形是菱形,
∵∠AOB=90°,OA=1,OB=2,
∴AB=
∴四边形的周长为4,
21.150°.
解:∵四边形ABCD是正方形,△CBE是等边三角形,
∴AD=CD=BC,∠ADC=90°,BE=CB=CE,∠EBC=∠BEC=60°,
∴AB=BE,∠ABE=30°,
∴∠BEA=(180°﹣30°)=75°,
同理:∠CED=75°,
∴∠AED=360°﹣75°﹣75°﹣60°=150°,
22.114°
∵∠DEF
=22°
长方形ABCD的对边AD//BC
∴∠EFB=∠DEF=22°
由折叠,
∠EFB处折叠了3层
∴∠CFE=180°
-3∠EFB
=180°—3
×
22°
=114°
23.24.
解:由作图可知,AG平分∠BAF,AB=AF,
∴AG垂直平分BF,∠FAG=∠BAE,
∴EF=EB,
∵AD∥BE,
∴∠FAE=∠AEB,
∴∠BAE
=∠AEB,
∴AB=BE,
∴AB=BE=EF=AF,
∴四边形ABEF是菱形,
∴BO=FO=4,
∴,
AE=6,
菱形的面积为;
24.(1)见解析;(2)
(1)证明:∵四边形ABCD是矩形,O是BD的中点,
∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,
∴∠OBE=∠ODF,
又∵∠BOE=∠DOF,
∴△BOE≌△DOF(ASA),
∴EO=FO,
∴四边形BEDF是平行四边形;
(2)解:当四边形BEDF是菱形时,BE=DE,
设BE=x,则
DE=x,AE=6﹣x,
在Rt△ADE中,DE2=AD2+AE2,
∴x2=42+(6﹣x)2,
解得:x=
,
∵DF=DE=.
25.证明见解析
解:∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90°,
∵△AEF是等边三角形,
∴AE=AF,∠AEF=∠AFE=60°,
∵∠CEF=45°,
∴∠CFE=∠CEF=45°,
∴∠AFD=∠AEB=180°﹣45°﹣60°=75°,
∴△AEB≌△AFD(AAS),
∴AB=AD,
∴矩形ABCD是正方形.
26.(1)证明见解析;(2)4
.
解:(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,
在△AEH与△CGF中,
,
∴△AEH≌△CGF(SAS);
∴EH=FG
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.
又∵AE=CG,AH=CF,
∴BE=DG,BF=DH,
在△BEF与△DGH中,
,
∴△BEF≌△DGH(SAS),
∴EF=GH.
∴四边形EFGH是平行四边形,
∴HG∥EF,
∴∠HGE=∠FEG,
∵EG平分∠HEF,
∴∠HEG=∠FEG,
∴∠HEG=∠HGE,
∴HE=HG,
又四边形EFGH是平行四边形,
∴四边形EFGH是菱形.
(2)连接HF交EG于O,则OF⊥EG,OE=EG.
∵四边形EFGH是菱形,
∴EG⊥FH,∠FEO=∠HEF=30°,
∵EF=4,
∴OF=EF=2
∴由勾股定理得,OE=2,
∴EG=2EO=4.
27.(1)证明见解析;(2)证明见解析.
解:(1)证明:∵E,G分别是AC,DC的中点,
∴EG是△ACD的中位线,
∴EG∥AD,
∵∠FCA=∠CEG,
∴EG∥CF,
∴AD∥CF;
(2)证明:由(1)得:AD∥CF,
∴∠DAE=∠FCE,∠ADE=∠CFE,
∵E是AC的中点,
∴AE=CE,
∴△ADE≌△CFE(AAS),
∴AD=CF,
∴四边形ADCF是平行四边形,
又∵AB=AC,AD是BC边上的中线,
∴AD⊥BC,
∴∠ADC=90°,
∴平行四边形ADCF是矩形.
28.(1)见解析;(2)的垂直平分线上,理由见解析;(3),理由见解析
解:(1)证明:由菱形的性质可得,,
由平移可得,,;
∴,,
∴四边形为平行四边形;
(2)当点运动到的垂直平分线上时,四边形为矩形.
∵菱形中,,
∴,,
∵,
∴,即,
又∵四边形为平行四边形,
∴四边形为矩形;
(3)如图,连接,
由(1)得四边形为平行四边形,
∴,
又∵,
∴是的中位线,
∴,
由菱形的轴对称可得,即,
∴.
一、单选题
1.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6cm,BC=8cm.则EF的长是(
)
A.2.2cm
B.2.3cm
C.2.4cm
D.2.5cm
2.如图,RtABC≌RtDCB,其中∠ABC=90°,AB=3,BC=4,O为BC中点,EF过点交AC、BD于点E、F,连接BE、CF,则下列结论错误(
)
A.四边形BECF为平行四边形
B.当BF=3.5时,
四边形BECF为矩形
C.当BF=2.5时,四边形BECF为菱形
D.四边形BECF不可能为正方形
3.如图,在菱形中,标出了四条线段的长度,其中有一个长度是标错的,这个长度是(
)
A.2
B.3
C.4
D.5
4.如图,在平行四边形中,,平分交于点,若,则的度数是(
)
A.10°
B.15°
C.20°
D.25°
5.如图,在中,于点D,正方形CDEF的顶点E在线段AD上,G是边EF上一点,连结AG,记面积为,面积为,若,则DE的长为(
)
A.
B.
C.4
D.8
6.如图,中,,以为边作如图所示的等边,等边,等边,连结,则四边形的面积为(
)
A.
B.
C.
D.1
7.如图,已知在菱形中,,以点为圆心,取大于的长为半径,分别作弧相交于两点,作直线交边于点(作图痕迹如图所示),连结,若,则下列结论错误的是(
)
A.
B.
C.菱形的面积为
D.
8.如图,正方形的边长为,的平分线交于点E,若点P,Q分别是和上的动点.则的最小值是(
)
A.
B.4
C.
D.
9.如图,在菱形ABCD中,E、F分别是AB、CD上的点,且AE=CF,EF与AC相交于点O,连接BO.若∠DAC=36°,则∠OBC的度数为(
)
A.36°
B.54°
C.64°
D.72°
10.如图,矩形中,过对角线上一点作//,分别交于点,交于点,连接,已知.与的面积和等于(
)
A.15
B.12
C.10
D.7
11.如图,菱形的边长为10,对角线=16,点分别是边的中点,连接并延长与的延长线相交于点,则长为(
)
A.13
B.10
C.12
D.5
12.如图,在等边△ABC中,BC=8cm,射线AGBC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以3cm/s的速度运动.设运动时间为t(s),当t=( )s时,以A、C、E、F为顶点的四边形是平行四边形.
A.1或2
B.2
C.2或3
D.2或4
13.如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A.2
B.2
C.3
D.4
14.如图,在△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
A.5
B.2.5
C.4.8
D.2.4
15.如图,平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=56°,则∠B=(
)
A.56°
B.60°
C.64°
D.68°
16.如图,把一张矩形纸片沿对角线折叠,点B的对应点为,与相交于点E,则下列结论不一定正确的是(
)
A.
B.
C.
D.
17.如图,在平行四边形中,M、N是上两点,,连接、、、,添加一个条件,使四边形是矩形,这个条件是(
)
A.
B.
C.
D.
18.如图,正方形中,点E为对角线上一点,交边于F,连接交线段于点H,延长交边于点Q,连接.下列结论:①;②若,,则;③;④若,,则;其中正确的有(
)个.
A.1个
B.2个
C.3个
D.4个
二、填空题
19.如图,矩形的对角线,交于点,若、分别为,的中点,若,则的长为________.
20.如图,把一张长方形的纸片对折两次,量出,,然后沿剪下一个,展开后得到一个四边形,则这个四边形的周长为___.
21.如图,四边形ABCD是正方形,△CBE是等边三角形,则∠AEB=__.
22.如图a是长方形纸带,∠DEF=22°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是________°.
23.如图,在中,按以下步骤作图:①以点A为圆心,的长为半径画弧,交于点F;②分别以点F,B为圆心,以大于的长为半径画弧,两弧在内交于点G;③作射线,交边于点E,交于点O,连接.若,,则四边形的面积为_________.
三、解答题
24.如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求DF的长.
25.如图,等边△AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
26.如图,在平行四边形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,AE=CG,AH=CF,且EG平分∠HEF.
(1)求证:四边形EFGH是菱形;
(2)若EF=4,∠HEF=60°,求EG的长.
27.如图,已知在△ABC中AB=AC,AD是BC边上的中线,E,G分别是AC,DC的中点,F为DE延长线上的点,∠FCA=∠CEG.
(1)求证:AD∥CF;
(2)求证:四边形ADCF是矩形.
28.如图1,在菱形中,,,点为上一动点,在点的运动过程中,始终保持,,连接,,与相交于点.
(1)如图1,求证四边形为平行四边形;
(2)当点运动到什么位置时,四边形为矩形?并说明理由;
(3)如图2,延长到,使,连接,判断与的数量关系,并说明理由.
参考答案
1.D
解:∵四边形ABCD是矩形,
∴∠ABC=90°,BD=AC,BO=OD,
∵AB=6cm,BC=8cm,
∴由勾股定理得:AC===10(cm),
∴BD=10cm,DO=5cm,
∵点E、F分别是AO、AD的中点,
∴EF是△AOD的中位线,
∴EF=OD=2.5cm,
2.B
证明:∵RtABC≌RtDCB,
∴∠ACB=∠CBD,
∴BD∥AC,
∵O为BC中点,
∴OB=OC,
∵∠BOF=∠COE,
∴△BOF≌△COE,
∴BF=CE,
∴四边形BECF为平行四边形,故A选项正确;
∵∠ABC=90°,AB=3,BC=4,
∴AC=5,
∵BF=3.5,
∴CE=BF=3.5,AE=1.5,
∵,
∴∠BEC不是直角,故四边形BECF不为矩形,故B选项错误;
当BF=2.5时,则CE=BF=2.5,
∴AE=2.5,
∴AE=CE,
∴,
∴四边形BECF为菱形,故C选项正确;
∵AB=3,BC=4,AC=5,
∴,
∴四边形BECF不可能为正方形,故D选项正确;
3.A
解:∵四边形是菱形,
∴∠DOC=90°,AB=CD=5,
∵,
∴3、4、5没标错,
∵OA=OC=3,
∴2标错了,
4.C
解:∵平行四边形
∴AD∥BC,AB=DC,∠B=∠ADC
∴∠AEB=∠DAE
∵平分
∴∠BAE=∠DAE
∴∠BAE=∠AEB
∵
∴△BAE是等边三角形
∴∠BAE=∠DAE
=,AB=AE=BE
∴AE=DC,∠ADC=∠DAE
∵AD=AD
∴△EAD≌△CDA
∴∠DAC=∠ADE
∵AD∥BC
∴∠DAC=∠ACE=∠ADE=∠DAC
∵
∴∠DAC=∠ACE=∠ADE=∠DAC=40°
∴=120?
∴=180???∠ACE=20?
5.A
解:,
,
,
,
,
,
,
,
,
四边形是正方形,
,,
,
,
,
,
,
,
,
,
,
,
,
,
.
6.B
解:如图,过点作于,设与于,
,,
,,
以、、为边作如图所示的等边,等边,等边,
,,,
,
,,
,
,
,
,
,
,
在和中,
,
,
,
同理可求,
,
四边形是菱形,
,,
,
,
四边形的面积,
7.C
解:由作法知,MN是线段AB的垂直平分线
∴BE=AE=2
故选项B正确
∵BE=AE,∠A=30゜
∴∠EBA=∠A=30゜
∵四边形ABCD是菱形
∴AB=AD
∴∠ABD=∠ADB=(180゜?∠A)=75゜
∴∠DBE=∠ABD?∠EBA=45゜
故选项A正确
设MN交AB于点F,如图
∵MN⊥AB,∠A=30゜
∴EF=AE=1
由勾股定理得:
∴AD=AB=2AF=
∴ED=AD?AE==?2
故选项D正确
如图,过点D作DG⊥AB于点G
在Rt△ADG中,∠A=30゜,则
∴
从而选项C错误
8.B
解:作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,
∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=,
∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=32,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=32,
∴P′D′=4,即DQ+PQ的最小值为4,
9.B
解:∵四边形ABCD是菱形,
∴AB=BC=AD=CD,AB∥CD,AD∥BC,
∴∠EAO=∠FCO,∠DAC=∠ACB=36°,
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴AO=CO,
又∵AB=BC,
∴BO⊥AC,
∴∠OBC=90°﹣∠ACB=54°,
10.C
解:作PM⊥AB于P,交DC于Q.
则有四边形DEMQ,四边形QMFC,四边形AEMP,四边形MPBF都是矩形,
∴S△DEM=S△DQM,S△QCM=S△MFC,S△AEM=S△APM,S△MPB=S△MFB,S△ABC=S△ADC,
∴S△ABC-S△AMP-S△MCF=S△ADC-S△AEM-S△MQC,
∴S四边形DEMQ=S四边形MPBF,
∵DE=CF=2,
∴S△DEM=S△MFB=×2×5=5,
∴S△DEM+S△MFB=5+5=10,
11.C
解:连接BD,交AC于点O,如图:
∵菱形ABCD的边长为10,点E、F分别是边CD、BC的中点,
∴AB∥CD,AB=BC=CD=DA=10,EF∥BD,
∵AC、BD是菱形的对角线,AC=16,
∴AC⊥BD,AO=CO=8,OB=OD,
又∵AB∥CD,EF∥BD,
∴DE∥BG,BD∥EG,
∴四边形BDEG是平行四边形,
∴BD=EG,
在△COD中,∵OC⊥OD,CD=10,CO=8,
∴OB=OD=,
∴BD=2OD=12,
∴EG=BD=12;
12.D
解:当点F在C的左侧时,根据题意得:AE=tcm,BF=3tcm,
则CF=BC﹣BF=(8﹣3t)cm,
∵AG∥BC,
∴当AE=CF时,四边形AECF是平行四边形,
即t=8﹣3t,
解得:t=2;
当点F在C的右侧时,根据题意得:AE=tcm,BF=3tcm,
则CF=BF﹣BC=(3t﹣8)cm,
∵AG∥BC,
∴当AE=CF时,四边形AEFC是平行四边形,
即t=3t﹣8,
解得:t=4;
综上可得:当t=2或4s时,以A、C、E、F为顶点四边形是平行四边形,
13.D
解:设BE与AC交于点P',连接BD.
∵点B与D关于AC对称,
∴P'D=P'B,
∴P'D+P'E=P'B+P'E=BE最小.
∵正方形ABCD的面积为16,
∴AB=4,
又∵△ABE是等边三角形,
∴BE=AB=4.
14.D
解:连接AP,如图所示:
∵∠BAC=90°,AB=6,AC=8,
∴BC==10,
∵PE⊥AB,PF⊥AC,
∴四边形AFPE是矩形,
∴EF=AP,EF与AP互相平分,
∵M是EF的中点,
∴M为AP的中点,
∴PM=AP,
根据直线外一点到直线上任一点的距离,垂线段最短,
即AP⊥BC时,AP最短,同样PM也最短,
∴当AP⊥BC时,AP==4.8,
∴AP最短时,AP=4.8,
∴当PM最短时,PM=AP=2.4.
15.D
解:取BC的中点G,连接EG、FG,
∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∵CE⊥AB,
∴∠CEB=90°,
∴EG=BG=CG,
∴∠B=∠GEB,
∵BC=2AB,
∴EG=AB=CD,
∴∠EFG=∠FEG,
∵F点为AD的中点,G为BC的中点,
∴FG∥AB,
∴∠AEF=∠EFG=56°,
∴∠FEG=56°,
∴∠GEB=180°-56°-56°=68°,
∴∠B=68°.
16.D
解:∵四边形ABCD是矩形,
∴,CD∥AB,AD∥BC,
∴,,
由折叠性质得:,,,
∴,,
∴,,
,即,
故选项A、B、C正确,选项D错误,
17.D
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD
∵对角线BD上的两点M、N满足BM=DN,
∴OB-BM=OD-DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵2OM=AC,
∴MN=AC,
∴四边形AMCN是矩形.
18.D
解:如图,连接BE,
∵四边形ABCD为正方形,
∴CB=CD,∠BCE=∠DCE=45°,
在△BEC和△DEC中,
,
∴△DCE≌△BCE(SAS),
∴DE=BE,∠CDE=∠CBE,
∴∠ADE=∠ABE,
∵∠DAB=90°,∠DEF=90°,
∴∠ADE+∠AFE=180°,
∵∠AFE+∠EFB=180°,
∴∠ADE=∠EFB,
∴∠ABE=∠EFB,
∴EF=BE,
∴DE=EF,故①正确;
∵∠DEF=90°,DE=EF,
∴∠EDF=∠DFE=45°,
如图:延长BC到G,使CG=AF,连接DG,
在△ADF和△CDG中,
,
∴△ADF≌△CDG(SAS),
∴∠AFD=∠G,∠ADF=∠CDG,DF=DG,
∵∠ADF+∠CDQ=90°?∠FDQ=45°,
∴∠CDG+∠CDQ=45°=∠GDQ,
∴∠GDQ=∠FDQ,
又∵DG=DF,DQ=DQ,
∴△QDF≌△QDG(SAS),
∴FQ=QG,∠G=∠DFQ,
∴∠DFA=∠DFQ,故③正确;
∵AB=6,CQ=3,
∴BQ=3,FB=6?AF,FQ=QG=3+AF,
∵FQ2=FB2+BQ2,
∴(3+AF)2=9+(6?AF)2,
∴AF=2,故②正确;
如图:将△CDE绕点A顺时针旋转90°得到△ADM,连接MH,
∴△CDE≌△ADM,
∴AM=CE=4,∠DCE=∠DAM=45°,∠ADM=∠CDE,DM=DE,
∴∠MAH=90°,∠ADM+∠ADH=∠CDE+∠ADH=45°=∠MDH,
又∵DH=DH,
∴△DMH≌△DEH(SAS),
∴EH=MH,
∵MH==,
∴EH=MH=,
∴AC=AH+EH+EC=6+
∴AB=AC÷=,故④正确;
19.6
解:∵四边形是矩形,,
∴,,
∵、分别为,的中点,
∴;
20.4
解:由题意,四边形是菱形,
∵∠AOB=90°,OA=1,OB=2,
∴AB=
∴四边形的周长为4,
21.150°.
解:∵四边形ABCD是正方形,△CBE是等边三角形,
∴AD=CD=BC,∠ADC=90°,BE=CB=CE,∠EBC=∠BEC=60°,
∴AB=BE,∠ABE=30°,
∴∠BEA=(180°﹣30°)=75°,
同理:∠CED=75°,
∴∠AED=360°﹣75°﹣75°﹣60°=150°,
22.114°
∵∠DEF
=22°
长方形ABCD的对边AD//BC
∴∠EFB=∠DEF=22°
由折叠,
∠EFB处折叠了3层
∴∠CFE=180°
-3∠EFB
=180°—3
×
22°
=114°
23.24.
解:由作图可知,AG平分∠BAF,AB=AF,
∴AG垂直平分BF,∠FAG=∠BAE,
∴EF=EB,
∵AD∥BE,
∴∠FAE=∠AEB,
∴∠BAE
=∠AEB,
∴AB=BE,
∴AB=BE=EF=AF,
∴四边形ABEF是菱形,
∴BO=FO=4,
∴,
AE=6,
菱形的面积为;
24.(1)见解析;(2)
(1)证明:∵四边形ABCD是矩形,O是BD的中点,
∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,
∴∠OBE=∠ODF,
又∵∠BOE=∠DOF,
∴△BOE≌△DOF(ASA),
∴EO=FO,
∴四边形BEDF是平行四边形;
(2)解:当四边形BEDF是菱形时,BE=DE,
设BE=x,则
DE=x,AE=6﹣x,
在Rt△ADE中,DE2=AD2+AE2,
∴x2=42+(6﹣x)2,
解得:x=
,
∵DF=DE=.
25.证明见解析
解:∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90°,
∵△AEF是等边三角形,
∴AE=AF,∠AEF=∠AFE=60°,
∵∠CEF=45°,
∴∠CFE=∠CEF=45°,
∴∠AFD=∠AEB=180°﹣45°﹣60°=75°,
∴△AEB≌△AFD(AAS),
∴AB=AD,
∴矩形ABCD是正方形.
26.(1)证明见解析;(2)4
.
解:(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,
在△AEH与△CGF中,
,
∴△AEH≌△CGF(SAS);
∴EH=FG
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.
又∵AE=CG,AH=CF,
∴BE=DG,BF=DH,
在△BEF与△DGH中,
,
∴△BEF≌△DGH(SAS),
∴EF=GH.
∴四边形EFGH是平行四边形,
∴HG∥EF,
∴∠HGE=∠FEG,
∵EG平分∠HEF,
∴∠HEG=∠FEG,
∴∠HEG=∠HGE,
∴HE=HG,
又四边形EFGH是平行四边形,
∴四边形EFGH是菱形.
(2)连接HF交EG于O,则OF⊥EG,OE=EG.
∵四边形EFGH是菱形,
∴EG⊥FH,∠FEO=∠HEF=30°,
∵EF=4,
∴OF=EF=2
∴由勾股定理得,OE=2,
∴EG=2EO=4.
27.(1)证明见解析;(2)证明见解析.
解:(1)证明:∵E,G分别是AC,DC的中点,
∴EG是△ACD的中位线,
∴EG∥AD,
∵∠FCA=∠CEG,
∴EG∥CF,
∴AD∥CF;
(2)证明:由(1)得:AD∥CF,
∴∠DAE=∠FCE,∠ADE=∠CFE,
∵E是AC的中点,
∴AE=CE,
∴△ADE≌△CFE(AAS),
∴AD=CF,
∴四边形ADCF是平行四边形,
又∵AB=AC,AD是BC边上的中线,
∴AD⊥BC,
∴∠ADC=90°,
∴平行四边形ADCF是矩形.
28.(1)见解析;(2)的垂直平分线上,理由见解析;(3),理由见解析
解:(1)证明:由菱形的性质可得,,
由平移可得,,;
∴,,
∴四边形为平行四边形;
(2)当点运动到的垂直平分线上时,四边形为矩形.
∵菱形中,,
∴,,
∵,
∴,即,
又∵四边形为平行四边形,
∴四边形为矩形;
(3)如图,连接,
由(1)得四边形为平行四边形,
∴,
又∵,
∴是的中位线,
∴,
由菱形的轴对称可得,即,
∴.
