高中数学人教A版(2019)必修二 8.3 棱柱、棱锥、棱台的表面积和体积(含解析)
文档属性
| 名称 | 高中数学人教A版(2019)必修二 8.3 棱柱、棱锥、棱台的表面积和体积(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 516.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-18 08:52:10 | ||
图片预览




文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
高中数学人教A版(2019)必修二
8.3
棱柱、棱锥、棱台的表面积和体积
一、单选题(共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.在直三棱柱
中,
,
,若该直三棱柱的外接球表面积为
,则此直三棱柱的高为(?
??).
A.?4????????????????????????????????????????B.?3????????????????????????????????????????C.?????????????????????????????????????????D.?
2.已知四棱锥
中,底面
是矩形,侧面
是正三角形,且侧面
底面
,
,若四棱锥
外接球的体积为
,则该四棱锥的表面积为(???
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
3.如图,一个四棱柱形容器中盛有水,在底面
中,
,
,
,侧棱
,若侧面
水平放置时,水面恰好过
的中点,那么当底面
水平放置时,水面高为(???
)
A.?2???????????????????????????????????????????B.????????????????????????????????????????????C.?3???????????????????????????????????????????D.?
4.已知点
,
,
在半径为5的球面上,且
,
,
为球面上的动点,则三棱锥
体积的最大值为(???
)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
5.在棱长为
的正方体
中,
为正方形
的中心,
,
,
分别为
,
,
的中点,则四面体
的体积为(???
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
6.如图,位于西安大慈恩寺的大雁塔,是唐代玄奘法师为保存经卷佛像而主持修建的,是我国现存最早的四方楼阁式砖塔.塔顶可以看成一个正四棱锥,其侧棱与底面所成的角为
,则该正四棱锥的一个侧面与底面的面积之比为(???
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
7.已知四棱锥
,底面
为矩形,点
在平面
上的射影为
的中点
.若
,
,
,则四棱锥
的表面积等于(???
)
A.?????????????????????B.?
C.?????????????????????D.?
8.已知正方体
的棱长为2,则三棱锥
的体积为(???
)
A.????????????????????????????????????????????B.????????????????????????????????????????????C.?4???????????????????????????????????????????D.?6
9.某中学开展劳动实习,学习加工制作食品包装盒.现有一张边长为6的正六边形硬纸片,如图所示,裁掉阴影部分,然后按虚线处折成高为
的正六棱柱无盖包装盒,则此包装盒的体积为(
??)
A.?144????????????????????????????????????????B.?72????????????????????????????????????????C.?36????????????????????????????????????????D.?24
二、多选题(共2小题,每小题5分,共10分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.)
10.若四面体各棱的长是1或2,且该四面体的棱长不全相等,则其体积的值可能为(???
)
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
11.攒尖是我国古代建筑中屋顶的一种结构形式,宋代称为最尖,清代称攒尖,通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖,也有单檐和重檐之分,多见于亭阁式建筑,园林建筑.下面以四角攒尖为例,如图,它的屋顶部分的轮廓可近似看作一个正四棱锥.已知此正四棱锥的侧面与底面所成的锐二面角为
,这个角接近
,若取
,侧棱长为
米,则(???
)
A.?正四棱锥的底面边长为6米??????????????????????????????????B.?正四棱锥的底面边长为3米
C.?正四棱锥的侧面积为
平方米?????????????????????D.?正四棱锥的侧面积为
平方米
三、填空题(共7小题,每小题5分,共35分)
12.如图,长方体
的体积是120,E为
的中点,则三棱锥E-BCD的体积是________.
13.在棱长为
的正方体
中,点
分别是线段
(不包括端点)上的动点,且线段
平行于平面
,则四面体
的体积的最大值是________.
14.已知正四棱锥
中,
是边长为3的等边三角形,点M是
的重心,过点M作与平面PAC垂直的平面
,平面
与截面PAC交线段的长度为2,则平面
与正四棱椎
表面交线所围成的封闭图形的面积可能为________.(请将可能的结果序号填到横线上)①2;②
;③3;
④
.
15.古希腊数学家阿波罗尼斯发现:平面上到两定点
、
距离之比
是常数的点的轨迹是一个圆心在直线
上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:在棱长为2的正方体
中,点
是正方体的表面
(包括边界)上的动点,若动点
满足
,则点
所形成的阿氏圆的半径为________;若
是
的中点,且满足
,则三棱锥
体积的最大值是________.
阿波罗尼奥斯
16.《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”;四个面均为直角三角形的四面体称为“鳖臑”.如图在堑堵
中,
,且
.下述四个结论正确结论的编号是________.
①四棱锥
为“阳马”
②四面体
为“鳖臑”
③过
点分别作
于点
,
于点
,则
④四棱锥
体积最大为
17.在边长为4的正方形ABCD内剪去四个全等的等腰三角形(如图1中阴影部分),折叠成底面边长为
的正四棱锥SEFGH(如图2),则正四棱锥SEFGH的体积为________.
18.已知正四棱锥
的体积为
,底面边长为2,则侧棱
的长为________.
四、解答题(共3小题,满分30分.解答应写出文字说明、证明过程或演算步骤.)
19.如图,已知四棱台的两底面均为正方形,且边长分别为
和
,侧面积为
,求其体积
20.长方体
中,
=12,
=10,
=6,过
作长方体的截面
使它成为正方形,
(1)求截面
将正方体分成的两部分的体积比;
(2)求
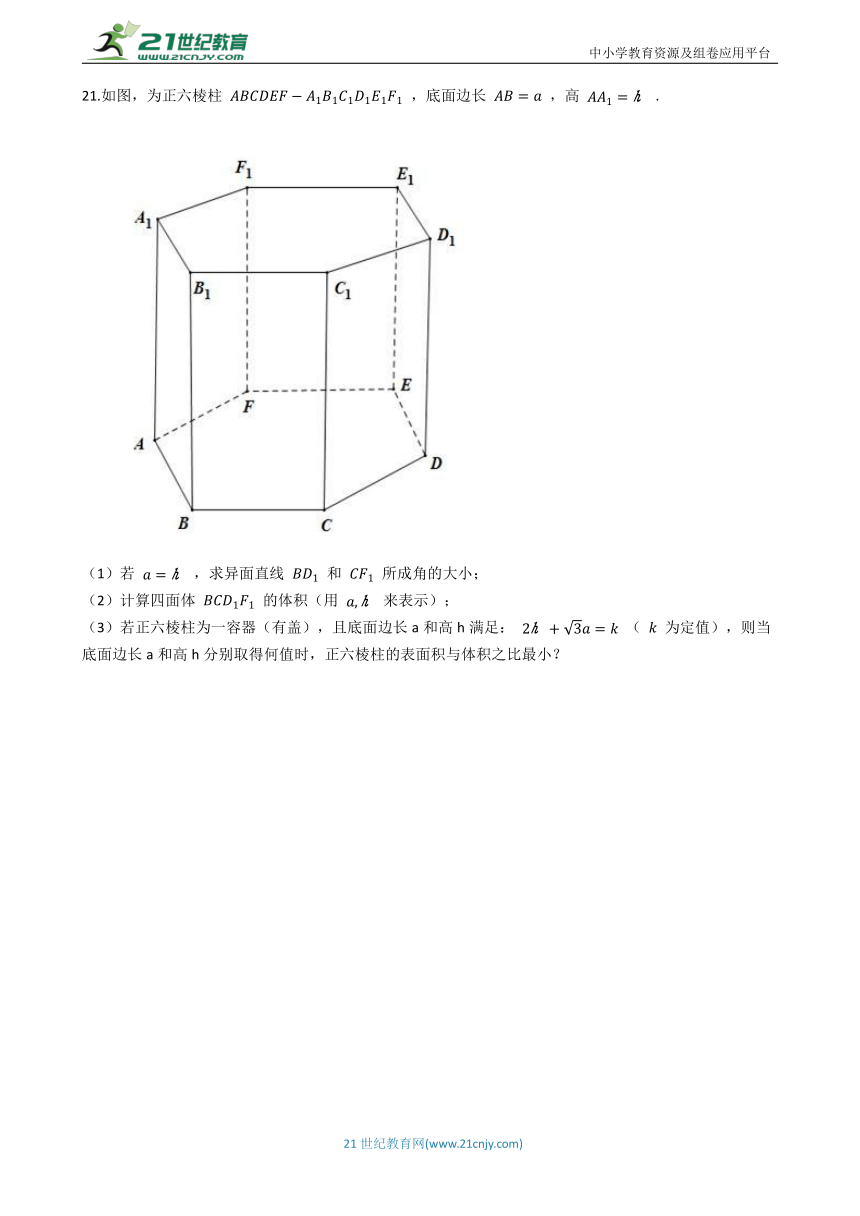
21.如图,为正六棱柱
,底面边长
,高
.
(1)若
,求异面直线
和
所成角的大小;
(2)计算四面体
的体积(用
来表示);
(3)若正六棱柱为一容器(有盖),且底面边长a和高h满足:
(
为定值),则当底面边长a和高h分别取得何值时,正六棱柱的表面积与体积之比最小?
答案解析部分
一、单选题
1.【答案】
D
【解析】解:因为
,所以将直三棱柱
补成长方体
,则直三棱柱的外接球就是长方体的外接球,外接球的直径等于长方体的体对角线,
设球的半径为
,则
,解得
,
设直三棱柱的高为
,则
,即
,
解得
,所以直三棱柱的高为
,
故答案为:D
【分析】因为
,所以将直三棱柱
补成长方体
,则直三棱柱的外接球就是长方体的外接球,外接球的直径等于长方体的体对角线,再利用勾股定理求出长方体的体对角线的长,进而求出外接球的直径,从而求出外接球的半径长,再利用勾股定理求出直三棱柱的高。
2.【答案】
B
【解析】设四棱锥
外接球的球心为
,过
作底面
的垂线,垂足为
,
因为四边形
是长方形,所以
的底面中心,即对角线
的交点,
过
作三角形
的垂线,垂足为
,所以
是正三角形
外心,
设外接球半径为
,外接球的体积为
,所以
,即
,
过
作
,则
是
的中点,连接
,所以
,
,
因为平面
平面
,平面
平面
,
所以
平面
,所以
,所以
平面
,所以
,
所以四边形
是平行四边形,即
,设
,则
,
,
所以
,由勾股定理得
,即
,
解得
,所以
,
,
因为
,所以
平面
,
平面
,
所以
,
,
,
因为
,
,
作
于
,所以
为
的中点,所以
,所以
,
,
所以
。
故答案为:B.
【分析】设四棱锥
外接球的球心为
,过
作底面
的垂线,垂足为
,因为四边形
是长方形,所以
的底面中心,即对角线
的交点,过
作三角形
的垂线,垂足为
,所以
是正三角形
外心,再利用球的体积公式结合已知条件,进而求出球的半径长,过
作
,则
是
的中点,连接
,所以
,
,因为平面
平面
,再利用面面垂直的性质定理推出线面垂直,所以
平面
,所以
,所以
平面
,所以
,所以四边形
是平行四边形,即
,设
,再利用勾股定理结合已知条件,进而求出x的值,所以
,
再利用三角形面积公式结合
,所以
平面
,
平面
,再利用线面垂直的定义证出线线垂直,即
,
,
再利用等面积法结合三角形面积公式,进而结合勾股定理,进而结合中点的性质求出PH的长,再利用三角形面积和矩形面积公式结合求和法,进而求出该四棱锥的表面积。
3.【答案】
B
【解析】设四棱柱的底面梯形的高为
,
的中点分别为
,
所求的水面高为h,
则水的体积
,
所以
,
故答案为:B。
【分析】设四棱柱的底面梯形的高为
,
的中点分别为
,所求的水面高为h,再利用四棱柱的体积公式,进而求出水的体积,再结合已知条件,进而求出水面的高。
4.【答案】
A
【解析】如图,因为
是
的外心,
是球心,
平面
,当
是
的延长线与球面交点时,
到平面
距离最大,
由
,
,得
,则
,
,
,
,
,
又
,
所以最大的
。
故答案为:A.
【分析】因为
是
的外心,
是球心,
平面
,当
是
的延长线与球面交点时,
到平面
距离最大,由
,
,结合余弦函数的定义得
,再利用同角三角函数基本关系式得出
,再利用正弦函数的定义求出AM的长,再利用勾股定理求出OM的长,进而求出PM的长,再利用三角形面积公式结合三棱锥体积公式,进而求出三棱锥
体积的最大值。
5.【答案】
B
【解析】如图所示,连接
交
于点
,连接
,连接
,
由正方体的特点可知,
,
,则根据线面垂直的判定定理可知
平面
,则
,
,故
。
故答案为:B.
【分析】连接
交
于点
,连接
,连接
,由正方体的结构特征可知,
,
,再利用线线垂直找出线面垂直,即
平面
,再利用三棱锥的体积公式结合求和法,进而利用三角形的面积等于梯形的面积减去三角形的面积的方法,从而求出四面体
的体积
。
6.【答案】
D
【解析】塔顶是正四棱锥
,如图,
是正四棱锥的高,
设底面边长为
,底面积为
,
,
,∴
,
是正三角形,面积为
,
所以
。
故答案为:D.
【分析】塔顶是正四棱锥
,结合已知条件和正方形面积公式,进而求出正四棱锥的底面积。再利用已知条件结合三角形
是正三角形,再结合三角形的面积公式,进而求出侧面三角形的面积,从而求出该正四棱锥的一个侧面与底面的面积之比。
7.【答案】
A
【解析】连接
,
平面
,
平面
,所以
,
同理
,
又
,
,
平面
,所以
平面
,而
平面
,所以
,同理
,
因此
,
,
,同理
,
,
,同理
,
是等腰三角形,所以底边上的高为
,
,
所以所求表面积为
。
故答案为:A.
【分析】连接
,
再利用
平面
结合线面垂直的定义推出线线垂直,所以
,同理
,又因为
,再利用线线垂直证出线面垂直,
所以
平面
,再结合线面垂直的定义推出线线垂直,所以
,同理
,再利用三角形面积公式和矩形的面积公式,进而得出
,同理
,
,再利用勾股定理结合等腰三角形的性质,进而求出底边上的高,再利用四棱锥的表面积公式,进而求出四棱锥
的表面积。
8.【答案】
B
【解析】如图三棱锥
是由正方体
截去四个小三棱锥
又因为
,
,
所以
。
故答案为:B
【分析】因为三棱锥
是由正方体
截去四个小三棱锥
再利用正方体的体积公式结合三棱锥的体积公式,再结合等体积法和作差法,进而求出三棱锥
的体积。
9.【答案】
B
【解析】如图:由正六边形的每个内角为
,
按虚线处折成高为
的正六棱柱,即
,
所以
可得正六棱柱底边边长
,
所以正六棱柱体积:
.
故答案为:B
【分析】
利用正六边形的性质求出正六棱柱的底边边长,再根据棱柱的体积公式求解.
二、多选题
10.【答案】
A,B,C
【解析】根据三角形的两边之和大于第三边性质,知四面体中棱长为1的棱最多有3条,
(1)若只有一条棱长度为1,如图
,其余棱长都为2,
取
中点
,
中点
,连接
,则
,又
是平面
内两相交直线,则
平面
,
由已知
,则
,
,
,
;
(2)若有两条棱长度为1,还是如(1)中的图形,
,
解法如(1),只是有
,
,
;
(3)若有两条棱长度为1,如图
,
,四面体为正三棱锥,设
是正三棱锥的高,
是
的外心,
,
,
,
.
故答案为:ABC.
【分析】
根据题意分情况讨论即可得出:分底边长为2,2,2,侧棱长为2,2,1,底边长为1,1,1,侧棱长为2,2,2和底面边长为2,2,1,侧棱长为2,2,1,三种情况分别计算棱锥的体积,结合选项得答案.
11.【答案】
A,C
【解析】如图,在正四棱锥
中,
O为正方形
的中心,
为
的中点,
则
,
设底面边长为
.
因为
,
所以
.
在
中,
,
所以
,底面边长为6米,
平方米.
故答案为:AC.
【分析】根据题意作出直观图,结合已知条件求解棱锥的底面边长,侧面积,判断选项的正误即可.
三、填空题
12.【答案】
10
【解析】
在长方体中,
平面
又
在
上,
平面
是三棱锥E-BCD的高,
长方体的体积为:
长方体
的体积是120,
又
为
的中点,
又
【分析】根据长方体的结构特征结合线面垂直和中点的性质,用三棱锥体积公式结合三棱锥体积与长方体体积的关系式,用长方体的体积求出三棱锥的体积。
13.【答案】
【解析】由线面平行的性质定理知
,
∽
,
,
设
,则
,
到平面
的距离为
,则
,
所以
,所以四面体
的体积为
,
当
时,四面体
的体积取得最大值:
.
所以答案应填:
.
【分析】由题意可得
∽
,
设
,则
,
到平面
的距离为
,
求出四面体的体积,通过二次函数的最值,求出四面体体积的最大值。
14.【答案】
①③
【解析】设
,因为
为正四棱锥,易知平面
平面
,又
,平面
平面
,
平面
,所以
平面
,
过M作
∥
分别交棱
、
于点T、L,
则
平面
,由题意,
只需所作的平面
是包含
且与截面PAC交线段的长度为2即可,
又
是边长为3的等边三角形,点M是
的重心,过M作
∥
分别交棱
、
于点E、Q,所以
,即
,所以
,
如图1,则平面
为满足题意的平面
,因为
,所以
,所以
,所以
,故①正确;
如图2,过T作
∥
,过L作
∥
,
易知平面
为满足题意的平面
,
且
为两个全等的直角梯形,易知T、H分别为GE、EF的中点,所以
,
所以五边形
的面积
,
故③正确.当
∥
与
∥
是完全相同的,所以,综上选①③.
故答案为:①③
【分析】设
,因为
为正四棱锥,易知
平面
,过M作
∥
分别交棱
、
于点T、L,则
平面
,由题意,只需所作的平面
是包含
且与截面PAC交线段的长度为2即可,数形结合,作出截面即可得到答案.
15.【答案】
;
【解析】在
上取点
,在
延长线上取点
,使得
,
,则
是题中阿氏圆上的点,由题意
是阿氏圆的直径,
,则
,
,所以
,∴阿氏圆半径为
;
正方体中
,
都与侧面
垂直,从而与侧面
内的直线
垂直,
如图
,则
,∴
,即
在上述阿氏圆上,
∵
的面积是2为定值,因此只要
到平面
距离最大,则三棱锥
体积的最大,
由于
点在阿氏圆上,当
是阿氏圆与
交点
时,
到平面
距离最大,
此时
,因此
,
,
三棱锥
体积的最大值为
。
故答案为:
;
。
【分析】在
上取点
,在
延长线上取点
,使得
,
,则
是题中阿氏圆上的点,由题意
是阿氏圆的直径,
,则
,
,所以
,进而求出阿氏圆半径
;再利用相似三角形对应边成比例结合三角形
的面积是2为定值,因此只要
到平面
距离最大,则三棱锥
体积的最大,由于
点在阿氏圆上,当
是阿氏圆与
交点
时,
到平面
距离最大,从而利用勾股定理求出QD的长,再利用三棱锥的体积公式,进而求出三棱锥
体积的最大值。
16.【答案】
①②③
【解析】对于①:因为
为堑堵,
所以侧棱
平面
,
所以
,又
,
所以
平面
,满足“阳马”的定义:一条侧棱垂直于底面的四棱锥,
所以四棱锥
为“阳马”,故①正确;
对于②:因为
底面
,所以
,即
为直角三角形,
同理
也为直角三角形,
由①可得
平面
,所以
,即
为直角三角形,
因为
底面
,所以
又因为
,
所以
平面
,
所以
,即
为直角三角形,
所以四面体
的四个面全为直角三角形,即四面体
为“鳖臑”,故②正确;
对于③:由①可得
平面
,
平面
,
所以
,又
,
所以
平面
,所以
,
又
,所以
平面AEF,
所以
,故③正确;
对于④:设
,则矩形
的面积为
,
在
中,
,
所以四棱锥
体积
,故④错误,
故答案为:①②③
【分析】根据题意,结合线面垂直的判定定理,性质定理,锥体的体积公式,逐一分析选项即可得到答案。
17.【答案】
【解析】连结EG,HF,交点为O,正方形EFGH的对角线EG=2,EO=1,则点E到线段AB的距离为1,EB=
=
.SO=
=
=2,故正四棱锥SEFGH的体积为
×(
)2×2=
.
故答案为:
【分析】连结EG,HF,交点为O,正方形EFGH的对角线EG=2,EO=1,即可求出EB,SO,进而求出正四棱锥SEFGH的体积。
18.【答案】
【解析】设底面正方形
的中心为
,又底面边长为2可得
由
【分析】先设底面正方形
的中心为
,根据题意得到
,再由
求出
,结合勾股定理即可得出结果.
四、解答题
19.【答案】
解:取
的中点
,
的中点
,上、下底面的中心
,则
为斜高,四边形
为直角梯形,
∵
,
∴
,
在直角梯形
中,
,
,
∴
,
故该四棱台的体积为
【分析】取
的中点
,
的中点
,上、下底面的中心
,根据侧面积求出
,再求出棱台的高,即可求出体积.
20.【答案】
(1)解:
是正方形,
=12,
=10,
=6
,
,
截面
将正方体分成的两部分为三棱柱和四棱柱,且高
相等均为长方体侧棱长
,
(2)解:过点B作直线BG平行于
交
于点G,过G作
的垂线交
于H,如图:
则BG平行于平面
,则点B到面
的距离即为点G到面
的距离,
易证
平面
,即GH即为点G到面
的距离
【分析】(1)截面
将正方体分成的两部分为三棱柱和四棱柱,且高相同,利用
只需要求出底面积的比值即可.(2)过点B作直线BG平行于
交
于点G,则点B到面
的距离即为点G到面
的距离,过G作
的垂线交
于H,则易证GH即为点G到面
的距离,再代入
即可.
21.【答案】
(1)解:补形如图:延长
相交于G点,延长
相交于H点,连接
由正六边形性质知
是平行四边形,从而得
是直四棱柱,则
且
所以四边形
是平行四边形,所以
,
所以异面直线
和
所成角的大小即为直线
和
所成角的大小.
在三角形
中,由平面几何知识和余弦定理得:
,
,
,
?
(2)解:如图,建立分别以
为
轴的空间直角坐标系,
则
,
,
,
,
,
设平面
法向量为
?,
,令
,则
,
所以
到平面
的距离
又
,
,
,
?
?
(3)解:由题知,正六棱柱的表面积
正六棱柱的体积
?又
所以当
时,
有最大值,也即
取得最小值,
此时
,
【分析】(1)延长
相交于G点,延长
相交于H点,连接
,得
是直四棱柱,证明
,所以异面直线
和
所成角的大小即为直线
和
所成角的大小.解三角形可得.(2)建立空间直角坐标系,求出平面
法向量,求出
到平面
的距离,可得四面体
的体积.(3)求出正六棱柱的表面积
,
正六棱柱的体积
,利用已知条件,转化为二次函数求得最值,得解.
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
高中数学人教A版(2019)必修二
8.3
棱柱、棱锥、棱台的表面积和体积
一、单选题(共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.在直三棱柱
中,
,
,若该直三棱柱的外接球表面积为
,则此直三棱柱的高为(?
??).
A.?4????????????????????????????????????????B.?3????????????????????????????????????????C.?????????????????????????????????????????D.?
2.已知四棱锥
中,底面
是矩形,侧面
是正三角形,且侧面
底面
,
,若四棱锥
外接球的体积为
,则该四棱锥的表面积为(???
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
3.如图,一个四棱柱形容器中盛有水,在底面
中,
,
,
,侧棱
,若侧面
水平放置时,水面恰好过
的中点,那么当底面
水平放置时,水面高为(???
)
A.?2???????????????????????????????????????????B.????????????????????????????????????????????C.?3???????????????????????????????????????????D.?
4.已知点
,
,
在半径为5的球面上,且
,
,
为球面上的动点,则三棱锥
体积的最大值为(???
)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
5.在棱长为
的正方体
中,
为正方形
的中心,
,
,
分别为
,
,
的中点,则四面体
的体积为(???
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
6.如图,位于西安大慈恩寺的大雁塔,是唐代玄奘法师为保存经卷佛像而主持修建的,是我国现存最早的四方楼阁式砖塔.塔顶可以看成一个正四棱锥,其侧棱与底面所成的角为
,则该正四棱锥的一个侧面与底面的面积之比为(???
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
7.已知四棱锥
,底面
为矩形,点
在平面
上的射影为
的中点
.若
,
,
,则四棱锥
的表面积等于(???
)
A.?????????????????????B.?
C.?????????????????????D.?
8.已知正方体
的棱长为2,则三棱锥
的体积为(???
)
A.????????????????????????????????????????????B.????????????????????????????????????????????C.?4???????????????????????????????????????????D.?6
9.某中学开展劳动实习,学习加工制作食品包装盒.现有一张边长为6的正六边形硬纸片,如图所示,裁掉阴影部分,然后按虚线处折成高为
的正六棱柱无盖包装盒,则此包装盒的体积为(
??)
A.?144????????????????????????????????????????B.?72????????????????????????????????????????C.?36????????????????????????????????????????D.?24
二、多选题(共2小题,每小题5分,共10分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.)
10.若四面体各棱的长是1或2,且该四面体的棱长不全相等,则其体积的值可能为(???
)
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
11.攒尖是我国古代建筑中屋顶的一种结构形式,宋代称为最尖,清代称攒尖,通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖,也有单檐和重檐之分,多见于亭阁式建筑,园林建筑.下面以四角攒尖为例,如图,它的屋顶部分的轮廓可近似看作一个正四棱锥.已知此正四棱锥的侧面与底面所成的锐二面角为
,这个角接近
,若取
,侧棱长为
米,则(???
)
A.?正四棱锥的底面边长为6米??????????????????????????????????B.?正四棱锥的底面边长为3米
C.?正四棱锥的侧面积为
平方米?????????????????????D.?正四棱锥的侧面积为
平方米
三、填空题(共7小题,每小题5分,共35分)
12.如图,长方体
的体积是120,E为
的中点,则三棱锥E-BCD的体积是________.
13.在棱长为
的正方体
中,点
分别是线段
(不包括端点)上的动点,且线段
平行于平面
,则四面体
的体积的最大值是________.
14.已知正四棱锥
中,
是边长为3的等边三角形,点M是
的重心,过点M作与平面PAC垂直的平面
,平面
与截面PAC交线段的长度为2,则平面
与正四棱椎
表面交线所围成的封闭图形的面积可能为________.(请将可能的结果序号填到横线上)①2;②
;③3;
④
.
15.古希腊数学家阿波罗尼斯发现:平面上到两定点
、
距离之比
是常数的点的轨迹是一个圆心在直线
上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:在棱长为2的正方体
中,点
是正方体的表面
(包括边界)上的动点,若动点
满足
,则点
所形成的阿氏圆的半径为________;若
是
的中点,且满足
,则三棱锥
体积的最大值是________.
阿波罗尼奥斯
16.《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”;四个面均为直角三角形的四面体称为“鳖臑”.如图在堑堵
中,
,且
.下述四个结论正确结论的编号是________.
①四棱锥
为“阳马”
②四面体
为“鳖臑”
③过
点分别作
于点
,
于点
,则
④四棱锥
体积最大为
17.在边长为4的正方形ABCD内剪去四个全等的等腰三角形(如图1中阴影部分),折叠成底面边长为
的正四棱锥SEFGH(如图2),则正四棱锥SEFGH的体积为________.
18.已知正四棱锥
的体积为
,底面边长为2,则侧棱
的长为________.
四、解答题(共3小题,满分30分.解答应写出文字说明、证明过程或演算步骤.)
19.如图,已知四棱台的两底面均为正方形,且边长分别为
和
,侧面积为
,求其体积
20.长方体
中,
=12,
=10,
=6,过
作长方体的截面
使它成为正方形,
(1)求截面
将正方体分成的两部分的体积比;
(2)求
21.如图,为正六棱柱
,底面边长
,高
.
(1)若
,求异面直线
和
所成角的大小;
(2)计算四面体
的体积(用
来表示);
(3)若正六棱柱为一容器(有盖),且底面边长a和高h满足:
(
为定值),则当底面边长a和高h分别取得何值时,正六棱柱的表面积与体积之比最小?
答案解析部分
一、单选题
1.【答案】
D
【解析】解:因为
,所以将直三棱柱
补成长方体
,则直三棱柱的外接球就是长方体的外接球,外接球的直径等于长方体的体对角线,
设球的半径为
,则
,解得
,
设直三棱柱的高为
,则
,即
,
解得
,所以直三棱柱的高为
,
故答案为:D
【分析】因为
,所以将直三棱柱
补成长方体
,则直三棱柱的外接球就是长方体的外接球,外接球的直径等于长方体的体对角线,再利用勾股定理求出长方体的体对角线的长,进而求出外接球的直径,从而求出外接球的半径长,再利用勾股定理求出直三棱柱的高。
2.【答案】
B
【解析】设四棱锥
外接球的球心为
,过
作底面
的垂线,垂足为
,
因为四边形
是长方形,所以
的底面中心,即对角线
的交点,
过
作三角形
的垂线,垂足为
,所以
是正三角形
外心,
设外接球半径为
,外接球的体积为
,所以
,即
,
过
作
,则
是
的中点,连接
,所以
,
,
因为平面
平面
,平面
平面
,
所以
平面
,所以
,所以
平面
,所以
,
所以四边形
是平行四边形,即
,设
,则
,
,
所以
,由勾股定理得
,即
,
解得
,所以
,
,
因为
,所以
平面
,
平面
,
所以
,
,
,
因为
,
,
作
于
,所以
为
的中点,所以
,所以
,
,
所以
。
故答案为:B.
【分析】设四棱锥
外接球的球心为
,过
作底面
的垂线,垂足为
,因为四边形
是长方形,所以
的底面中心,即对角线
的交点,过
作三角形
的垂线,垂足为
,所以
是正三角形
外心,再利用球的体积公式结合已知条件,进而求出球的半径长,过
作
,则
是
的中点,连接
,所以
,
,因为平面
平面
,再利用面面垂直的性质定理推出线面垂直,所以
平面
,所以
,所以
平面
,所以
,所以四边形
是平行四边形,即
,设
,再利用勾股定理结合已知条件,进而求出x的值,所以
,
再利用三角形面积公式结合
,所以
平面
,
平面
,再利用线面垂直的定义证出线线垂直,即
,
,
再利用等面积法结合三角形面积公式,进而结合勾股定理,进而结合中点的性质求出PH的长,再利用三角形面积和矩形面积公式结合求和法,进而求出该四棱锥的表面积。
3.【答案】
B
【解析】设四棱柱的底面梯形的高为
,
的中点分别为
,
所求的水面高为h,
则水的体积
,
所以
,
故答案为:B。
【分析】设四棱柱的底面梯形的高为
,
的中点分别为
,所求的水面高为h,再利用四棱柱的体积公式,进而求出水的体积,再结合已知条件,进而求出水面的高。
4.【答案】
A
【解析】如图,因为
是
的外心,
是球心,
平面
,当
是
的延长线与球面交点时,
到平面
距离最大,
由
,
,得
,则
,
,
,
,
,
又
,
所以最大的
。
故答案为:A.
【分析】因为
是
的外心,
是球心,
平面
,当
是
的延长线与球面交点时,
到平面
距离最大,由
,
,结合余弦函数的定义得
,再利用同角三角函数基本关系式得出
,再利用正弦函数的定义求出AM的长,再利用勾股定理求出OM的长,进而求出PM的长,再利用三角形面积公式结合三棱锥体积公式,进而求出三棱锥
体积的最大值。
5.【答案】
B
【解析】如图所示,连接
交
于点
,连接
,连接
,
由正方体的特点可知,
,
,则根据线面垂直的判定定理可知
平面
,则
,
,故
。
故答案为:B.
【分析】连接
交
于点
,连接
,连接
,由正方体的结构特征可知,
,
,再利用线线垂直找出线面垂直,即
平面
,再利用三棱锥的体积公式结合求和法,进而利用三角形的面积等于梯形的面积减去三角形的面积的方法,从而求出四面体
的体积
。
6.【答案】
D
【解析】塔顶是正四棱锥
,如图,
是正四棱锥的高,
设底面边长为
,底面积为
,
,
,∴
,
是正三角形,面积为
,
所以
。
故答案为:D.
【分析】塔顶是正四棱锥
,结合已知条件和正方形面积公式,进而求出正四棱锥的底面积。再利用已知条件结合三角形
是正三角形,再结合三角形的面积公式,进而求出侧面三角形的面积,从而求出该正四棱锥的一个侧面与底面的面积之比。
7.【答案】
A
【解析】连接
,
平面
,
平面
,所以
,
同理
,
又
,
,
平面
,所以
平面
,而
平面
,所以
,同理
,
因此
,
,
,同理
,
,
,同理
,
是等腰三角形,所以底边上的高为
,
,
所以所求表面积为
。
故答案为:A.
【分析】连接
,
再利用
平面
结合线面垂直的定义推出线线垂直,所以
,同理
,又因为
,再利用线线垂直证出线面垂直,
所以
平面
,再结合线面垂直的定义推出线线垂直,所以
,同理
,再利用三角形面积公式和矩形的面积公式,进而得出
,同理
,
,再利用勾股定理结合等腰三角形的性质,进而求出底边上的高,再利用四棱锥的表面积公式,进而求出四棱锥
的表面积。
8.【答案】
B
【解析】如图三棱锥
是由正方体
截去四个小三棱锥
又因为
,
,
所以
。
故答案为:B
【分析】因为三棱锥
是由正方体
截去四个小三棱锥
再利用正方体的体积公式结合三棱锥的体积公式,再结合等体积法和作差法,进而求出三棱锥
的体积。
9.【答案】
B
【解析】如图:由正六边形的每个内角为
,
按虚线处折成高为
的正六棱柱,即
,
所以
可得正六棱柱底边边长
,
所以正六棱柱体积:
.
故答案为:B
【分析】
利用正六边形的性质求出正六棱柱的底边边长,再根据棱柱的体积公式求解.
二、多选题
10.【答案】
A,B,C
【解析】根据三角形的两边之和大于第三边性质,知四面体中棱长为1的棱最多有3条,
(1)若只有一条棱长度为1,如图
,其余棱长都为2,
取
中点
,
中点
,连接
,则
,又
是平面
内两相交直线,则
平面
,
由已知
,则
,
,
,
;
(2)若有两条棱长度为1,还是如(1)中的图形,
,
解法如(1),只是有
,
,
;
(3)若有两条棱长度为1,如图
,
,四面体为正三棱锥,设
是正三棱锥的高,
是
的外心,
,
,
,
.
故答案为:ABC.
【分析】
根据题意分情况讨论即可得出:分底边长为2,2,2,侧棱长为2,2,1,底边长为1,1,1,侧棱长为2,2,2和底面边长为2,2,1,侧棱长为2,2,1,三种情况分别计算棱锥的体积,结合选项得答案.
11.【答案】
A,C
【解析】如图,在正四棱锥
中,
O为正方形
的中心,
为
的中点,
则
,
设底面边长为
.
因为
,
所以
.
在
中,
,
所以
,底面边长为6米,
平方米.
故答案为:AC.
【分析】根据题意作出直观图,结合已知条件求解棱锥的底面边长,侧面积,判断选项的正误即可.
三、填空题
12.【答案】
10
【解析】
在长方体中,
平面
又
在
上,
平面
是三棱锥E-BCD的高,
长方体的体积为:
长方体
的体积是120,
又
为
的中点,
又
【分析】根据长方体的结构特征结合线面垂直和中点的性质,用三棱锥体积公式结合三棱锥体积与长方体体积的关系式,用长方体的体积求出三棱锥的体积。
13.【答案】
【解析】由线面平行的性质定理知
,
∽
,
,
设
,则
,
到平面
的距离为
,则
,
所以
,所以四面体
的体积为
,
当
时,四面体
的体积取得最大值:
.
所以答案应填:
.
【分析】由题意可得
∽
,
设
,则
,
到平面
的距离为
,
求出四面体的体积,通过二次函数的最值,求出四面体体积的最大值。
14.【答案】
①③
【解析】设
,因为
为正四棱锥,易知平面
平面
,又
,平面
平面
,
平面
,所以
平面
,
过M作
∥
分别交棱
、
于点T、L,
则
平面
,由题意,
只需所作的平面
是包含
且与截面PAC交线段的长度为2即可,
又
是边长为3的等边三角形,点M是
的重心,过M作
∥
分别交棱
、
于点E、Q,所以
,即
,所以
,
如图1,则平面
为满足题意的平面
,因为
,所以
,所以
,所以
,故①正确;
如图2,过T作
∥
,过L作
∥
,
易知平面
为满足题意的平面
,
且
为两个全等的直角梯形,易知T、H分别为GE、EF的中点,所以
,
所以五边形
的面积
,
故③正确.当
∥
与
∥
是完全相同的,所以,综上选①③.
故答案为:①③
【分析】设
,因为
为正四棱锥,易知
平面
,过M作
∥
分别交棱
、
于点T、L,则
平面
,由题意,只需所作的平面
是包含
且与截面PAC交线段的长度为2即可,数形结合,作出截面即可得到答案.
15.【答案】
;
【解析】在
上取点
,在
延长线上取点
,使得
,
,则
是题中阿氏圆上的点,由题意
是阿氏圆的直径,
,则
,
,所以
,∴阿氏圆半径为
;
正方体中
,
都与侧面
垂直,从而与侧面
内的直线
垂直,
如图
,则
,∴
,即
在上述阿氏圆上,
∵
的面积是2为定值,因此只要
到平面
距离最大,则三棱锥
体积的最大,
由于
点在阿氏圆上,当
是阿氏圆与
交点
时,
到平面
距离最大,
此时
,因此
,
,
三棱锥
体积的最大值为
。
故答案为:
;
。
【分析】在
上取点
,在
延长线上取点
,使得
,
,则
是题中阿氏圆上的点,由题意
是阿氏圆的直径,
,则
,
,所以
,进而求出阿氏圆半径
;再利用相似三角形对应边成比例结合三角形
的面积是2为定值,因此只要
到平面
距离最大,则三棱锥
体积的最大,由于
点在阿氏圆上,当
是阿氏圆与
交点
时,
到平面
距离最大,从而利用勾股定理求出QD的长,再利用三棱锥的体积公式,进而求出三棱锥
体积的最大值。
16.【答案】
①②③
【解析】对于①:因为
为堑堵,
所以侧棱
平面
,
所以
,又
,
所以
平面
,满足“阳马”的定义:一条侧棱垂直于底面的四棱锥,
所以四棱锥
为“阳马”,故①正确;
对于②:因为
底面
,所以
,即
为直角三角形,
同理
也为直角三角形,
由①可得
平面
,所以
,即
为直角三角形,
因为
底面
,所以
又因为
,
所以
平面
,
所以
,即
为直角三角形,
所以四面体
的四个面全为直角三角形,即四面体
为“鳖臑”,故②正确;
对于③:由①可得
平面
,
平面
,
所以
,又
,
所以
平面
,所以
,
又
,所以
平面AEF,
所以
,故③正确;
对于④:设
,则矩形
的面积为
,
在
中,
,
所以四棱锥
体积
,故④错误,
故答案为:①②③
【分析】根据题意,结合线面垂直的判定定理,性质定理,锥体的体积公式,逐一分析选项即可得到答案。
17.【答案】
【解析】连结EG,HF,交点为O,正方形EFGH的对角线EG=2,EO=1,则点E到线段AB的距离为1,EB=
=
.SO=
=
=2,故正四棱锥SEFGH的体积为
×(
)2×2=
.
故答案为:
【分析】连结EG,HF,交点为O,正方形EFGH的对角线EG=2,EO=1,即可求出EB,SO,进而求出正四棱锥SEFGH的体积。
18.【答案】
【解析】设底面正方形
的中心为
,又底面边长为2可得
由
【分析】先设底面正方形
的中心为
,根据题意得到
,再由
求出
,结合勾股定理即可得出结果.
四、解答题
19.【答案】
解:取
的中点
,
的中点
,上、下底面的中心
,则
为斜高,四边形
为直角梯形,
∵
,
∴
,
在直角梯形
中,
,
,
∴
,
故该四棱台的体积为
【分析】取
的中点
,
的中点
,上、下底面的中心
,根据侧面积求出
,再求出棱台的高,即可求出体积.
20.【答案】
(1)解:
是正方形,
=12,
=10,
=6
,
,
截面
将正方体分成的两部分为三棱柱和四棱柱,且高
相等均为长方体侧棱长
,
(2)解:过点B作直线BG平行于
交
于点G,过G作
的垂线交
于H,如图:
则BG平行于平面
,则点B到面
的距离即为点G到面
的距离,
易证
平面
,即GH即为点G到面
的距离
【分析】(1)截面
将正方体分成的两部分为三棱柱和四棱柱,且高相同,利用
只需要求出底面积的比值即可.(2)过点B作直线BG平行于
交
于点G,则点B到面
的距离即为点G到面
的距离,过G作
的垂线交
于H,则易证GH即为点G到面
的距离,再代入
即可.
21.【答案】
(1)解:补形如图:延长
相交于G点,延长
相交于H点,连接
由正六边形性质知
是平行四边形,从而得
是直四棱柱,则
且
所以四边形
是平行四边形,所以
,
所以异面直线
和
所成角的大小即为直线
和
所成角的大小.
在三角形
中,由平面几何知识和余弦定理得:
,
,
,
?
(2)解:如图,建立分别以
为
轴的空间直角坐标系,
则
,
,
,
,
,
设平面
法向量为
?,
,令
,则
,
所以
到平面
的距离
又
,
,
,
?
?
(3)解:由题知,正六棱柱的表面积
正六棱柱的体积
?又
所以当
时,
有最大值,也即
取得最小值,
此时
,
【分析】(1)延长
相交于G点,延长
相交于H点,连接
,得
是直四棱柱,证明
,所以异面直线
和
所成角的大小即为直线
和
所成角的大小.解三角形可得.(2)建立空间直角坐标系,求出平面
法向量,求出
到平面
的距离,可得四面体
的体积.(3)求出正六棱柱的表面积
,
正六棱柱的体积
,利用已知条件,转化为二次函数求得最值,得解.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
