3.4 简单的图案设计 跟踪练习(含答案)
文档属性
| 名称 | 3.4 简单的图案设计 跟踪练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-16 18:55:37 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
3.4 简单的图案设计跟踪练习
一、选择题。
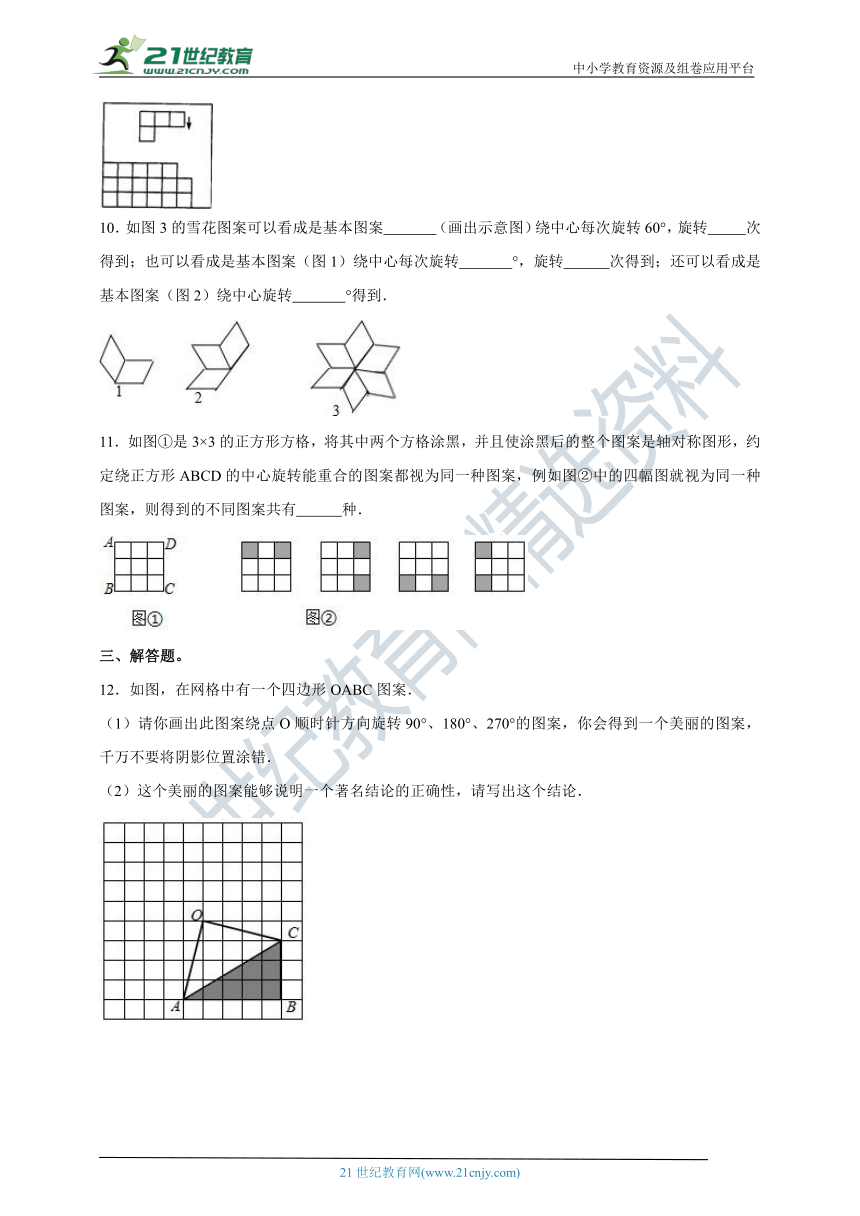
1.经过以下变化后所得到的三角形不能和△ABC全等的是( )
A.平移 B.翻折
C.旋转 D.放大
2.如图是4×4的网格图.将图中标有①、②、③、④的一个小正方形涂灰,使所有的灰色图形构成中心对称图形,则涂灰的小正方形是( )
A.① B.② C.③ D.④
3.如图,在9×6的方格纸中,小树从位置A经过平移旋转后到达位置B,下列说法中正确的是( )
A.先向右平移6格,再绕点B顺时针旋转45°
B.先向右平移6格,再绕点B逆时针旋转45°
C.先向右平移6格,再绕点B顺时针旋转90°
D.先向右平移6格,再绕点B逆时针旋转90°
4.如图,作△ABC关于直线l对称的图形△A'B'C',接着△A'B'C'沿着平行于直线l的方向向下平移,在这个变换过程中两个对应三角形的对应点应具有的性质是( )
A.对应点连线相等
B.对应点连线互相平行
C.对应点连线垂直于直线l
D.对应点连线被直线l平分
5.平面直角坐标系xOy中,点P(a,b)经过某种变换后得到的对应点为P′(a+1,b﹣1).已知A,B,C是不共线的三个点,它们经过这种变换后,得到的对应点分别为A′,B′,C′.若△ABC的面积为S1,△A′B′C′的面积为S2,则用等式表示S1与S2的关系为( )
A.S1=S2 B.S1=S2 C.S1=2S2 D.S1=4S2
6.如图,平面内某正方形内有一长为10宽为5的矩形,它可以在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,则该正方形边长的最小整数n为( )
A.10 B.11 C.12 D.13
二、填空题。
7.广告设计人员进行图案设计,经常将一个基本图案进行轴对称、平移和 等.
8.如图,在方格纸中,图形②可以看作是图形①经过若干次图形变化(平移、轴对称、旋转)得到的,写
出一种由图形①得到图形②的变化过程: .
9.有一种拼图游戏是当每一行的小方格铺满后,这一行消失并使玩家得分,若在游戏过程中,已拼好的图案如图,又出现了一小方格体向下运动,为了使所有图案消失,你必须将这个小方格 ,再 ,再 ,才能拼一个完整的图案,从而使图案消失.
10.如图3的雪花图案可以看成是基本图案 (画出示意图)绕中心每次旋转60°,旋转 次得到;也可以看成是基本图案(图1)绕中心每次旋转 °,旋转 次得到;还可以看成是基本图案(图2)绕中心旋转 °得到.
11.如图①是3×3的正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,约定绕正方形ABCD的中心旋转能重合的图案都视为同一种图案,例如图②中的四幅图就视为同一种图案,则得到的不同图案共有 种.
三、解答题。
12.如图,在网格中有一个四边形OABC图案.
(1)请你画出此图案绕点O顺时针方向旋转90°、180°、270°的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错.
(2)这个美丽的图案能够说明一个著名结论的正确性,请写出这个结论.
13.如图,DEF是三角形ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点坐标之间的关系,解答下面的问题:
(1)写出点A与点D,点B与点E,点C与点F的坐标,并说明这些对应点的坐标有何特征;
(2)若点P(a+4,﹣5﹣b)与点Q(2b,2a+8)也是通过上述变换得到的对应点,求a,b的值.
14.在小正方形构成的网格中,每个小正方形的顶点叫做格点.
(1)△ABC的三个顶点都在格点上.
①在图1中,画出一个与△ABC成中心对称的格点三角形;
②在图2中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;
③在图3中,画出△ABC绕着点C按顺时针方向旋转90°后的三角形.
(2)如图4是由5个边长为1的小正方形拼成的图形,请选择适当的格点,用无刻度的直尺画经过点P的一条直线,使它平分该图形的面积,保留连线的痕迹,不要求说明理由.
答案
一、选择题。
1.D.2.C.3.B.4.D.5.D.6.C.
二、填空题。
7.:旋转.
8.:图形①绕D点顺时针旋转90°,并向下平移3个单位得到图形②.
9.顺时针旋转90°,再向右平移,再向下平移,才能拼一个完整的图案,从而使图案消失.
10.:菱形,5,120,2,180;
11.:6.
解答题。
12.【解答】解:(1)如图所示:
(2)这个美丽的图案能够说明勾股定理:直角三角形中两直角边的平方和等于斜边的平方.
13.【解答】解:(1)它们的坐标分别是A(2,3),D(﹣2,﹣3),B(1,2),E(﹣1,﹣2),
C(3,1),F(﹣3,﹣1)
这些对应点横坐标互为相反数,纵坐标也是互为相反数.
(2)依题意得:a+4+2b=0且﹣5﹣b+2a+8=0,
∴a=﹣2,b=﹣1.
14.【解答】解:(1)①如图1中,△ABD即为所求.
②如图2中,△ACD即为所求.
③如图3中,△CEF即为所求.
(2)如图4中,直线PT即为所求.
_21?????????è?????(www.21cnjy.com)_
3.4 简单的图案设计跟踪练习
一、选择题。
1.经过以下变化后所得到的三角形不能和△ABC全等的是( )
A.平移 B.翻折
C.旋转 D.放大
2.如图是4×4的网格图.将图中标有①、②、③、④的一个小正方形涂灰,使所有的灰色图形构成中心对称图形,则涂灰的小正方形是( )
A.① B.② C.③ D.④
3.如图,在9×6的方格纸中,小树从位置A经过平移旋转后到达位置B,下列说法中正确的是( )
A.先向右平移6格,再绕点B顺时针旋转45°
B.先向右平移6格,再绕点B逆时针旋转45°
C.先向右平移6格,再绕点B顺时针旋转90°
D.先向右平移6格,再绕点B逆时针旋转90°
4.如图,作△ABC关于直线l对称的图形△A'B'C',接着△A'B'C'沿着平行于直线l的方向向下平移,在这个变换过程中两个对应三角形的对应点应具有的性质是( )
A.对应点连线相等
B.对应点连线互相平行
C.对应点连线垂直于直线l
D.对应点连线被直线l平分
5.平面直角坐标系xOy中,点P(a,b)经过某种变换后得到的对应点为P′(a+1,b﹣1).已知A,B,C是不共线的三个点,它们经过这种变换后,得到的对应点分别为A′,B′,C′.若△ABC的面积为S1,△A′B′C′的面积为S2,则用等式表示S1与S2的关系为( )
A.S1=S2 B.S1=S2 C.S1=2S2 D.S1=4S2
6.如图,平面内某正方形内有一长为10宽为5的矩形,它可以在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,则该正方形边长的最小整数n为( )
A.10 B.11 C.12 D.13
二、填空题。
7.广告设计人员进行图案设计,经常将一个基本图案进行轴对称、平移和 等.
8.如图,在方格纸中,图形②可以看作是图形①经过若干次图形变化(平移、轴对称、旋转)得到的,写
出一种由图形①得到图形②的变化过程: .
9.有一种拼图游戏是当每一行的小方格铺满后,这一行消失并使玩家得分,若在游戏过程中,已拼好的图案如图,又出现了一小方格体向下运动,为了使所有图案消失,你必须将这个小方格 ,再 ,再 ,才能拼一个完整的图案,从而使图案消失.
10.如图3的雪花图案可以看成是基本图案 (画出示意图)绕中心每次旋转60°,旋转 次得到;也可以看成是基本图案(图1)绕中心每次旋转 °,旋转 次得到;还可以看成是基本图案(图2)绕中心旋转 °得到.
11.如图①是3×3的正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,约定绕正方形ABCD的中心旋转能重合的图案都视为同一种图案,例如图②中的四幅图就视为同一种图案,则得到的不同图案共有 种.
三、解答题。
12.如图,在网格中有一个四边形OABC图案.
(1)请你画出此图案绕点O顺时针方向旋转90°、180°、270°的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错.
(2)这个美丽的图案能够说明一个著名结论的正确性,请写出这个结论.
13.如图,DEF是三角形ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点坐标之间的关系,解答下面的问题:
(1)写出点A与点D,点B与点E,点C与点F的坐标,并说明这些对应点的坐标有何特征;
(2)若点P(a+4,﹣5﹣b)与点Q(2b,2a+8)也是通过上述变换得到的对应点,求a,b的值.
14.在小正方形构成的网格中,每个小正方形的顶点叫做格点.
(1)△ABC的三个顶点都在格点上.
①在图1中,画出一个与△ABC成中心对称的格点三角形;
②在图2中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;
③在图3中,画出△ABC绕着点C按顺时针方向旋转90°后的三角形.
(2)如图4是由5个边长为1的小正方形拼成的图形,请选择适当的格点,用无刻度的直尺画经过点P的一条直线,使它平分该图形的面积,保留连线的痕迹,不要求说明理由.
答案
一、选择题。
1.D.2.C.3.B.4.D.5.D.6.C.
二、填空题。
7.:旋转.
8.:图形①绕D点顺时针旋转90°,并向下平移3个单位得到图形②.
9.顺时针旋转90°,再向右平移,再向下平移,才能拼一个完整的图案,从而使图案消失.
10.:菱形,5,120,2,180;
11.:6.
解答题。
12.【解答】解:(1)如图所示:
(2)这个美丽的图案能够说明勾股定理:直角三角形中两直角边的平方和等于斜边的平方.
13.【解答】解:(1)它们的坐标分别是A(2,3),D(﹣2,﹣3),B(1,2),E(﹣1,﹣2),
C(3,1),F(﹣3,﹣1)
这些对应点横坐标互为相反数,纵坐标也是互为相反数.
(2)依题意得:a+4+2b=0且﹣5﹣b+2a+8=0,
∴a=﹣2,b=﹣1.
14.【解答】解:(1)①如图1中,△ABD即为所求.
②如图2中,△ACD即为所求.
③如图3中,△CEF即为所求.
(2)如图4中,直线PT即为所求.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
