3.1.2 图形的平移 跟踪练习(含答案)
文档属性
| 名称 | 3.1.2 图形的平移 跟踪练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-16 18:56:43 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
3.1.2 图形的平移跟踪练习
一、选择题。
1.在平面直角坐标系中,将三角形各顶点的纵坐标都加上3,横坐标减去2,所得图形的位置与原图形相比( )
A.向左平移3个单位,向上平移2个单位
B.向上平移3个单位,向左平移2个单位
C.向下平移3个单位,向右平移2个单位
D.向上平移3个单位,向右平移2个单位
2.已知点,,若线段CD是由线段AB沿y轴方向向下平移2个单位得到的,则线段CD两端点的坐标分别为( )
A. B.
C. D.(2,0),(5,﹣2)
3.在如图所示的单位正方形网格中,三角形ABC经过平移后得到三角形A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,则P1点的坐标为( )
A.(1.4,﹣1) B.(1.5,2) C.(﹣1.6,﹣1) D.(2.4,1)
4.如图,已知一个斜边长为2的直角三角板的直角顶点与原点重合,两直角边分别落在两个坐标轴上.现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是( )
A.(1,0) B.(,) C.(1,) D.(﹣1,)
二、填空题。
5.在平面直角坐标系中,将点A(﹣2,1)先向右平移3个单位长度、再向上平移2个单位长度得点B,则点B坐标为 .
6.如图,△ABC沿着点B到点E的方向,平移到△DEF的位置,已知BC=5,EC=3,那么A、D两点间的距离为 .
7.如图,直角坐标系中,⊙A的半径为3,点A的坐标为(﹣3,﹣4),若将⊙A沿y轴方向平移,平移后,使⊙A上只有3个点到x轴的距离为2,则平移后点A的坐标为 .
8.如图,在平面直角坐标系xOy中,将四边形ABCD先向下平移,再向右平移得到四边形A1B1C1D1,已知A(﹣3,5),B(﹣4,3),A1(3,3),则B1的坐标为 .
9.已知点P的坐标为(a,b)(a>0),点Q的坐标为(c,2),且|a﹣c|+=0,将线段PQ向右平移a个单位长度,其扫过的面积为24,那么a+b+c的值为 .
三、解答题。
10.如图,在边长为1的小正方形网格中,△ABC的顶点都在格点上,建立适当的平面直角坐标系xOy,使得点A、B的坐标分别为(2,3)、(3,2).
(1)画出平面直角坐标系;
(2)画出将△ABC沿y轴翻折,再向左平移1个单位长度得到的△A'B'C';
(3)点P(m,n)是△ABC内部一点,写出点P经过(2)中两次变换后的对应点P′的坐标 .
11.如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)直线OC与AB有何位置关系?请说明理由.
(2)求∠EOB的度数;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
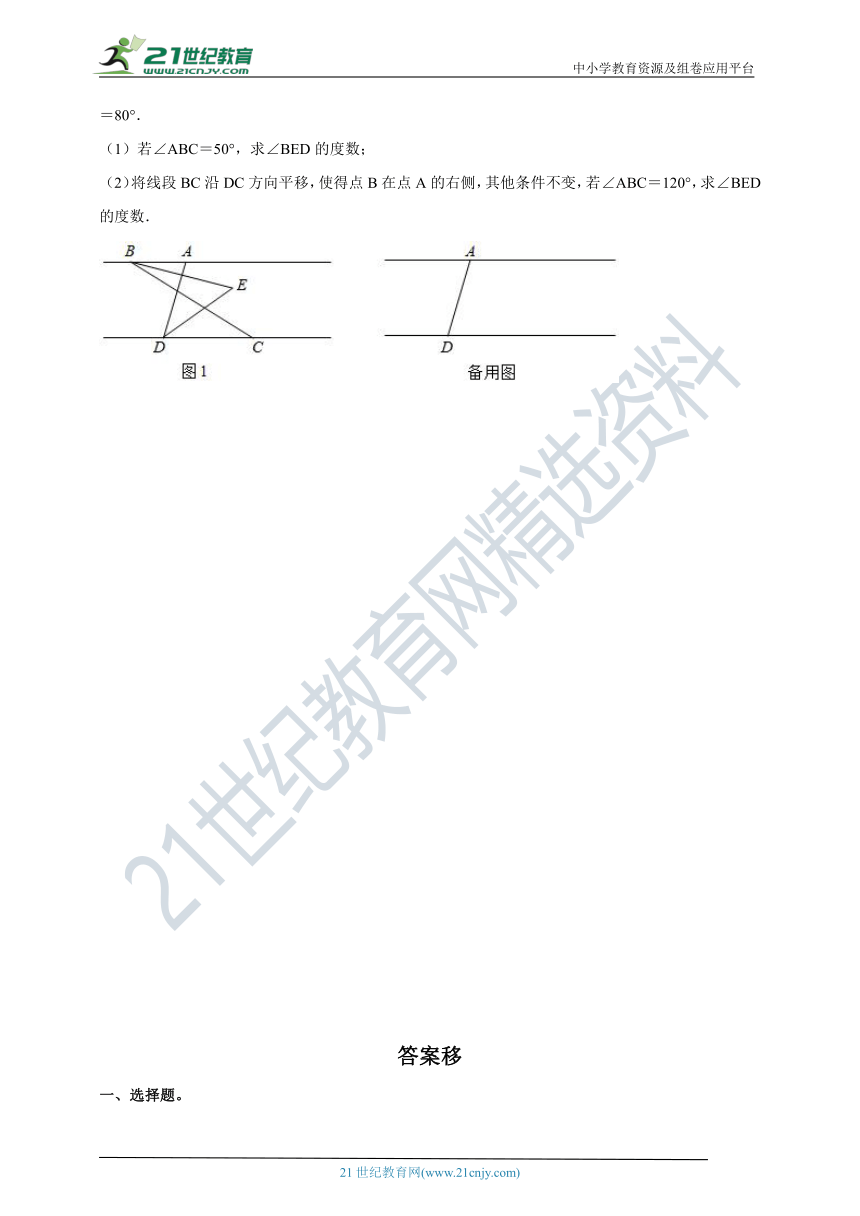
12.AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC=80°.
(1)若∠ABC=50°,求∠BED的度数;
(2)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,若∠ABC=120°,求∠BED的度数.
答案移
一、选择题。
1.B.2.C.3.C.4.C.
二、填空题。
5.:(1,3).
6.:2.
7.:(﹣3,﹣1)或(﹣3,1).
8.:(2,1).
9.18.
解答题。
10.【解答】解:(1)如图,平面直角坐标系即为所求作.
(2)如图,△A′B′C′即为所求作.
(3)由题意,P′(﹣m﹣1,n).
故答案为:(﹣m﹣1,n).
11.解答】解:(1)AB∥OC,理由如下:
∵CB∥OA,
∴∠ABC+∠OAB=180°,
∵∠C=∠OAB=100°,
∴∠C+∠ABC=180,
∴AB∥OC;
(2)∵CB∥OA,∠C=100°,
∴∠AOC=80°,
又∵∠FOB=∠AOB,OE平分∠COF,
∴∠EOB=∠BOF+∠EOF=(∠AOF+∠COF)=×80°=40°;
(3)存在,
∵在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=∠AOC=×80°=20°,
∴∠OEC=180°﹣∠C﹣∠COE=180°﹣100°﹣20°=60°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=60°.
12.【解答】解:(1)作EF∥AB,如图1,
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠ABC=25°,∠EDC=∠ADC=40°,
∵AB∥CD,
∴EF∥CD,
∵∠BEF=∠ABE=25°,∠FED=∠EDC=40°,
∴∠BED=25°+40°=65°;
(2)作EF∥AB,如图2,
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠ABC=60°,∠EDC=∠ADC=40°,
∵AB∥CD,
∴EF∥CD,
∵∠BEF=180°﹣∠ABE=120°,∠FED=∠EDC=40°,
∴∠BED=120°+40°=160°.
如图3,∵BE平分∠ABC,DE平分∠ADC,
∴∠1=∠ABC=60°,∠EDC=∠ADC=40°,
∵AB∥CD,
∴∠2=40°,
∵∠1=∠BED+∠2,
∴∠BED=60°﹣40°=20°.
如图4,∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠ABC=60°,∠2=∠ADC=40°,
∵AB∥CD,
∴∠1=∠ABE=60°,
∵∠3=∠2=40°,
而∠1=∠BED+∠2,
∴∠BED=60°﹣40°=20°.
综上所述,∠BED的度数为20°或160°.
_21?????????è?????(www.21cnjy.com)_
3.1.2 图形的平移跟踪练习
一、选择题。
1.在平面直角坐标系中,将三角形各顶点的纵坐标都加上3,横坐标减去2,所得图形的位置与原图形相比( )
A.向左平移3个单位,向上平移2个单位
B.向上平移3个单位,向左平移2个单位
C.向下平移3个单位,向右平移2个单位
D.向上平移3个单位,向右平移2个单位
2.已知点,,若线段CD是由线段AB沿y轴方向向下平移2个单位得到的,则线段CD两端点的坐标分别为( )
A. B.
C. D.(2,0),(5,﹣2)
3.在如图所示的单位正方形网格中,三角形ABC经过平移后得到三角形A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,则P1点的坐标为( )
A.(1.4,﹣1) B.(1.5,2) C.(﹣1.6,﹣1) D.(2.4,1)
4.如图,已知一个斜边长为2的直角三角板的直角顶点与原点重合,两直角边分别落在两个坐标轴上.现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是( )
A.(1,0) B.(,) C.(1,) D.(﹣1,)
二、填空题。
5.在平面直角坐标系中,将点A(﹣2,1)先向右平移3个单位长度、再向上平移2个单位长度得点B,则点B坐标为 .
6.如图,△ABC沿着点B到点E的方向,平移到△DEF的位置,已知BC=5,EC=3,那么A、D两点间的距离为 .
7.如图,直角坐标系中,⊙A的半径为3,点A的坐标为(﹣3,﹣4),若将⊙A沿y轴方向平移,平移后,使⊙A上只有3个点到x轴的距离为2,则平移后点A的坐标为 .
8.如图,在平面直角坐标系xOy中,将四边形ABCD先向下平移,再向右平移得到四边形A1B1C1D1,已知A(﹣3,5),B(﹣4,3),A1(3,3),则B1的坐标为 .
9.已知点P的坐标为(a,b)(a>0),点Q的坐标为(c,2),且|a﹣c|+=0,将线段PQ向右平移a个单位长度,其扫过的面积为24,那么a+b+c的值为 .
三、解答题。
10.如图,在边长为1的小正方形网格中,△ABC的顶点都在格点上,建立适当的平面直角坐标系xOy,使得点A、B的坐标分别为(2,3)、(3,2).
(1)画出平面直角坐标系;
(2)画出将△ABC沿y轴翻折,再向左平移1个单位长度得到的△A'B'C';
(3)点P(m,n)是△ABC内部一点,写出点P经过(2)中两次变换后的对应点P′的坐标 .
11.如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)直线OC与AB有何位置关系?请说明理由.
(2)求∠EOB的度数;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
12.AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC=80°.
(1)若∠ABC=50°,求∠BED的度数;
(2)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,若∠ABC=120°,求∠BED的度数.
答案移
一、选择题。
1.B.2.C.3.C.4.C.
二、填空题。
5.:(1,3).
6.:2.
7.:(﹣3,﹣1)或(﹣3,1).
8.:(2,1).
9.18.
解答题。
10.【解答】解:(1)如图,平面直角坐标系即为所求作.
(2)如图,△A′B′C′即为所求作.
(3)由题意,P′(﹣m﹣1,n).
故答案为:(﹣m﹣1,n).
11.解答】解:(1)AB∥OC,理由如下:
∵CB∥OA,
∴∠ABC+∠OAB=180°,
∵∠C=∠OAB=100°,
∴∠C+∠ABC=180,
∴AB∥OC;
(2)∵CB∥OA,∠C=100°,
∴∠AOC=80°,
又∵∠FOB=∠AOB,OE平分∠COF,
∴∠EOB=∠BOF+∠EOF=(∠AOF+∠COF)=×80°=40°;
(3)存在,
∵在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=∠AOC=×80°=20°,
∴∠OEC=180°﹣∠C﹣∠COE=180°﹣100°﹣20°=60°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=60°.
12.【解答】解:(1)作EF∥AB,如图1,
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠ABC=25°,∠EDC=∠ADC=40°,
∵AB∥CD,
∴EF∥CD,
∵∠BEF=∠ABE=25°,∠FED=∠EDC=40°,
∴∠BED=25°+40°=65°;
(2)作EF∥AB,如图2,
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠ABC=60°,∠EDC=∠ADC=40°,
∵AB∥CD,
∴EF∥CD,
∵∠BEF=180°﹣∠ABE=120°,∠FED=∠EDC=40°,
∴∠BED=120°+40°=160°.
如图3,∵BE平分∠ABC,DE平分∠ADC,
∴∠1=∠ABC=60°,∠EDC=∠ADC=40°,
∵AB∥CD,
∴∠2=40°,
∵∠1=∠BED+∠2,
∴∠BED=60°﹣40°=20°.
如图4,∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠ABC=60°,∠2=∠ADC=40°,
∵AB∥CD,
∴∠1=∠ABE=60°,
∵∠3=∠2=40°,
而∠1=∠BED+∠2,
∴∠BED=60°﹣40°=20°.
综上所述,∠BED的度数为20°或160°.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
