七年级数学第七章_三角形复习
文档属性
| 名称 | 七年级数学第七章_三角形复习 |  | |
| 格式 | zip | ||
| 文件大小 | 683.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-21 17:01:32 | ||
图片预览





文档简介
(共37张PPT)
第七章三角形
复 习
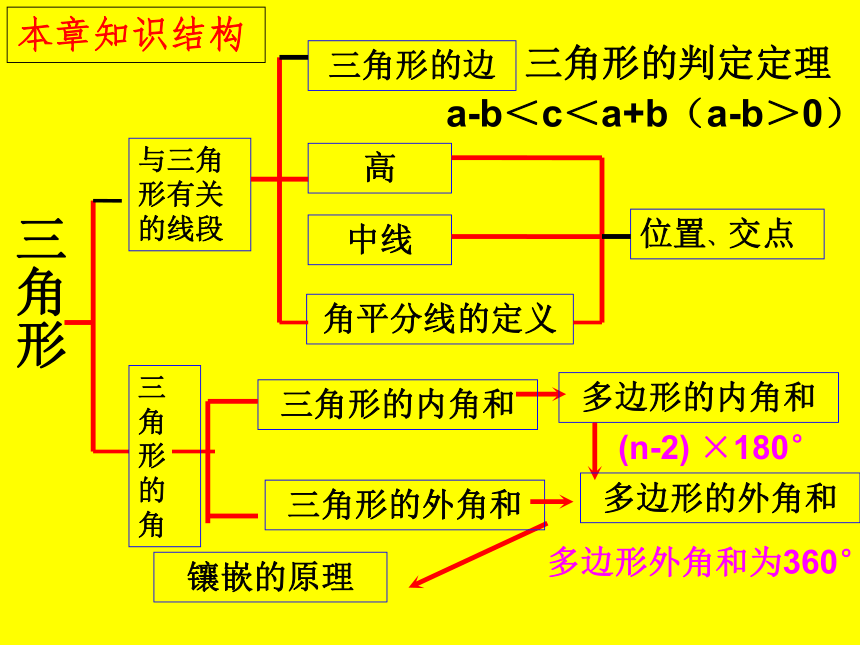
(n-2) ×180°
三角形
与三角形有关的线段
a-b<c<a+b(a-b>0)
高
三角形的边
三角形的判定定理
中线
角平分线的定义
位置、交点
三角形的内角和
多边形的内角和
多边形的外角和
三角形的外角和
多边形外角和为360°
镶嵌的原理
本章知识结构
三角形的角
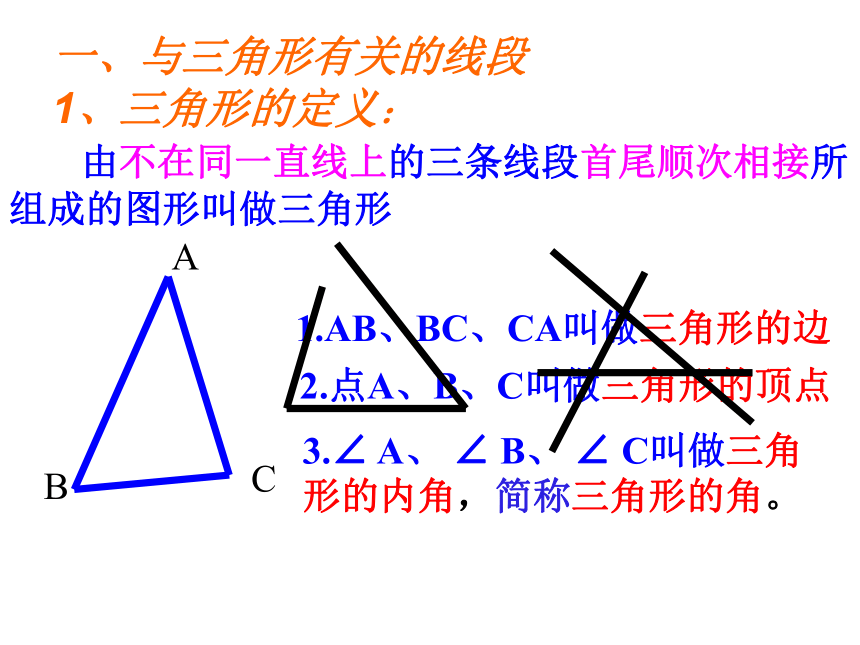
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形
A
C
B
1.AB、BC、CA叫做三角形的边
2.点A、B、C叫做三角形的顶点
3.∠ A、 ∠ B、 ∠ C叫做三角形的内角,简称三角形的角。
一、与三角形有关的线段
1、三角形的定义:
观察
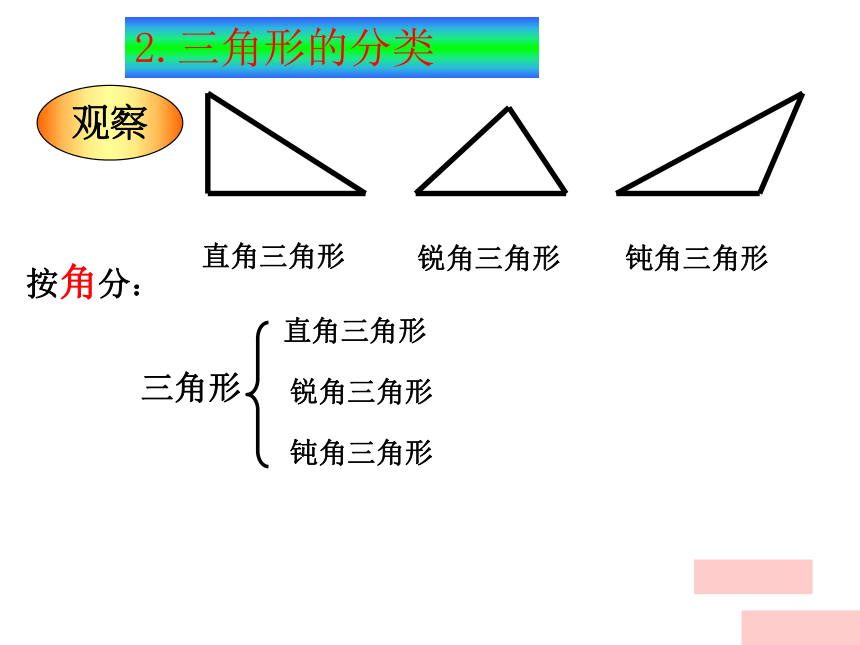
按角分:
直角三角形
锐角三角形
钝角三角形
2.三角形的分类
三角形
直角三角形
锐角三角形
钝角三角形
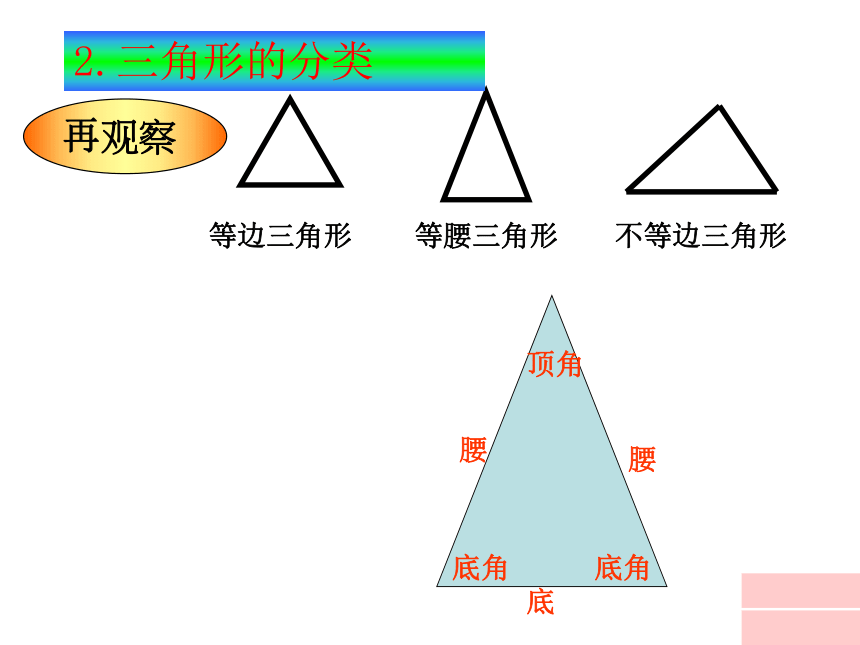
再观察
等边三角形
等腰三角形
不等边三角形
2.三角形的分类
腰
腰
底
顶角
底角
底角
1. 三角形的三边关系:
(1)三角形的任何两边之和大于第三边:
(2)三角形的任何两边之差小于第三边
(3)判断三条已知线段a、b、c能否组成三角形;
当a最长,且有b+c>a时,就可构成三角形。
(4)确定三角形第三边的取值范围:
两边之差<第三边<两边之和。
2. 三角形的三条高线(或高线所在的直线)交于一点,
锐角三角形三条高线交于三角形内部一点,
直角三角形三条高线交于直角顶点,
钝角三角形三条高线所在的直线交于三角形外部一点。
3. 三角形的三条中线交于三角形内部一点。
4. 三角形的三条角平分线交于三角形内部一点。
1、三角形两条边分别是2cm,7cm,则第三边c的范围为 。
2、等腰三角形的一边长为6cm,另一边长为12cm,则其周长( )
A、24cm B、30cm
C、24cM或30cm D、18cm
3、用7根火柴首尾顺次连结摆成一个三角形,能摆成不同的三角形的个数为 。
5(cm)<c<9(cm)
B
2
(3,3,1;2,2,3)
1、等腰三角形一边的长是
另一边的长是8,则它的周
长是 。
18或21
19
5
3
填一填
2、一个三角形的两边长分别是 和 ,第三边的长为奇数,则第三边的长为_____ .
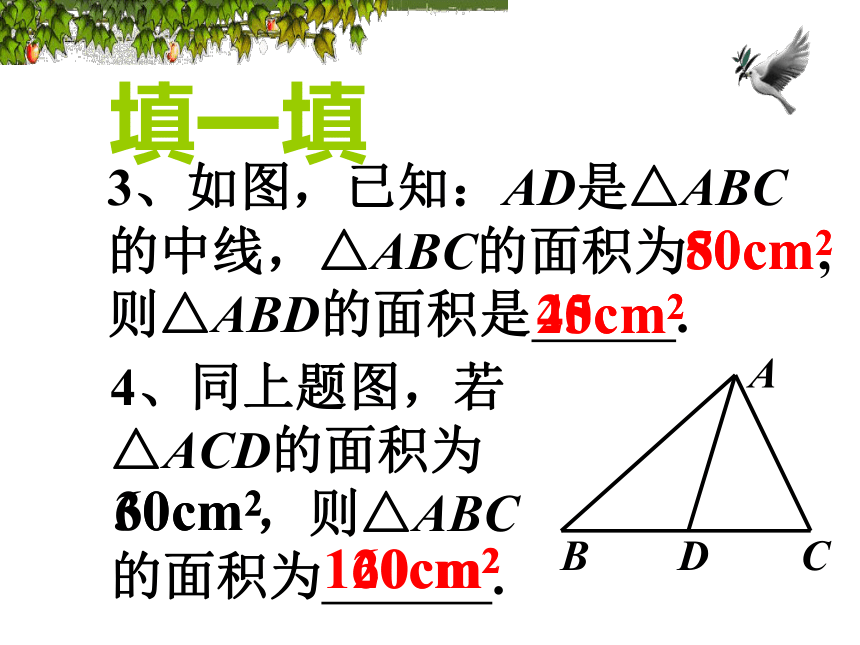
4、同上题图,若
△ACD的面积为
,则△ABC
的面积为 .
3、如图,已知:AD是△ABC
的中线,△ABC的面积为 ,则△ABD的面积是 .
A
B
C
D
50cm2
25cm2
80cm2
40cm2
60cm2
120cm2
30cm2
60cm2
填一填
5. 三角形具有稳定性,而四边形没有稳定性。
6. 三角形的内角
三角形内角和定理:三角形的三个内角和为
推论:直角三角形的两个锐角互余。
7. 三角形的外角:
定义:三角形一边与另一边的延长线组成的角叫做三角形的外角。
性质:1.三角形的一个外角等于与它不相邻的两个内角的和。
2.三角形的一个外角大于与它不相邻的任何一个内角。
3.三角形的一个外角与它相邻的内角互为邻补角。
8. 三角形的外角和:三角形的三个外角和为
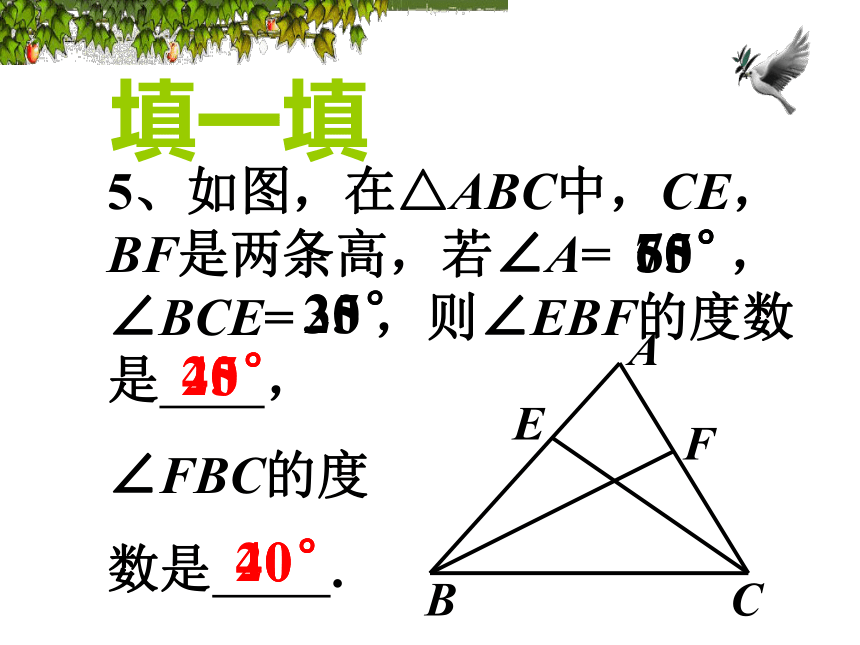
5、如图,在△ABC中,CE,BF是两条高,若∠A= ,∠BCE= ,则∠EBF的度数是 ,
∠FBC的度
数是 .
25°
20°
40°
30°
50°
65°
25°
40°
20°
70°
40°
A
B
C
E
F
填一填
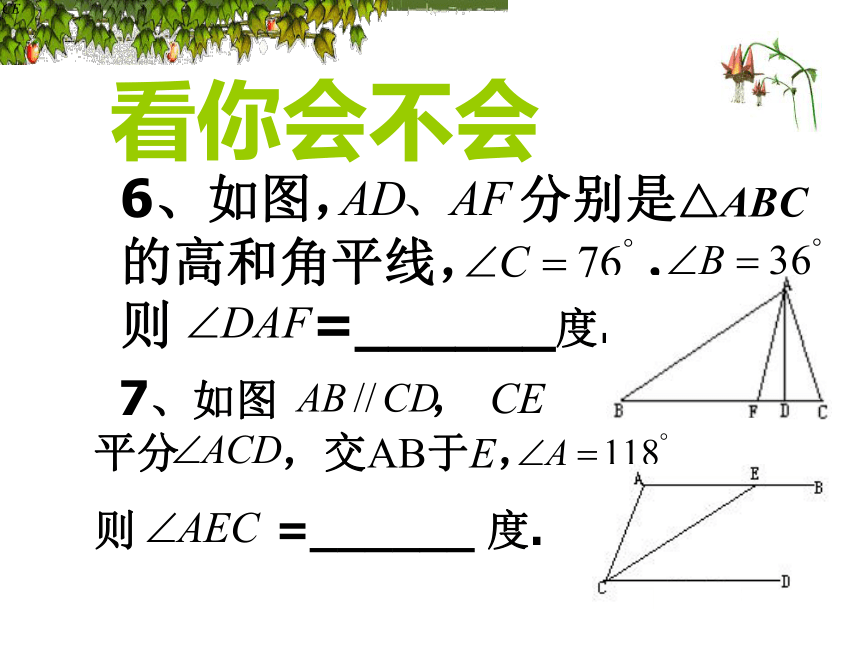
6、如图, 分别是△ABC的高和角平线, , 则 =______度.
7、如图 , 平分 ,交AB于E,
则 =______ 度.
看你会不会
题型考查
3、如图,CD是Rt△ABC斜边上的高,与∠A相等的角是 ,理由是 。
A
B
C
D
题型考查
4、如图,在△ABC中,两条角平分线BD和CE相交于点O,若∠BOC=116°,那么∠A的度数是 。
A
B
C
D
E
O
1∶2∶3
2∶3∶4
①∠A=380,∠B=730 , ∠C=
③∠B=400,∠A∶∠C=3∶4
∠C=
8、若三角形三个内角的度数
之比为 ,则这三个内角的度数分别是_______________.
1∶3∶6
180、540、1080
300、600、900
400、600、800
9、在△ABC中,根据下列条件,求∠C的度数.
690
②AB⊥BC,∠A=350 ∠C=
550
800
填一填
5、三角形中至少有一个角大于或等于( )
A、45° B、55° C、60° D、65°
6、如果直角三角形的一个锐角是另一个锐角的4倍,那么这个直角三角形中一个锐角的度数是( )
A、9° B、18° C、27° D、36°
题型考查
4.下列能说明∠1>∠2的是( )
A
B
D
C
1.符合条件∠A+∠B=62°的三角形是( )
A、4㎝ B、5㎝ C、9㎝ D、14㎝
C
3.如图,在△ABC中,∠A=70° ∠B=60°,点D在BC的延长线上,则 ∠ACD=____度.
130
A
B
C
D
2.在下列长度的四根木棒中,能与4㎝,9㎝两根木棒围成三角形的是( )
A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定
C
题型考查
n-3
n-2
1
2
3
2
3
4
2
5
9
n-3
n-2
3×1800
4×1800
(n-2)×1800
1
2
3
2
3
4
2×1800
3600
3600
3600
3600
1、记住以下角度:
(1)三角形的内角和为______;
180°
四边形的内角和为______;
360°
五边形的内角和为______;
540°
六边形的内角和为______;
720°
(2)正三角形的每个内角为______;
60°
正四边形的每个内角为______;
90°
正五边形的每个内角为______;
108°
正六边形的每个内角为______;
120°
10 、一个多边形的每一个外角都等于 ,则该多边形的内角和等于_____ 度.
11、下列边长为a的正多边形与边长为a的正方形组合起来(1)正三角形 (2)正五边形 (3)正六边形 (4)正八边形, 其中不能镶嵌成平面的是( )
A. (1) (2) B. (2) (3) C. (1) (3) D. (1) (4)
填一填
1440
D
5.如图所示:△ABC中,D,E分别为BC,AD的中点,且S △ABC=4,则S阴为_____
基础过关
A
F
E
D
B
C
O
6.如图所示:△ABC中,AD⊥BC于D, BE⊥AC于E, CF⊥AB于F,则△OBC的高是 。OF是哪些三角形的高?
OD
△OAB, △OAF, △OBF
1
7. 如图,则ABC的形状是( ) A、锐角三角形 B、钝角三角形
C、直角三角形 D、等腰三角形
8.如图, ∠A+∠B+∠C+∠D+∠E+∠F= ;
C
360°
基础过关
10.AB∥CD, ∠A=45°∠C=80°,则∠M=
11.如图,直线DE与△ABC的三边所在直线交与D、E、F,A=40°,D=25°,DE⊥AB,则∠ ACB=
基础过关
9、如果一个三角形的各内角与一个外角的
和是225°,则与这个外角相邻的内角是____度.
1350
350
750
12.若一个三角形的三个外角度数之比为3:4:5,则与之相邻的三个内角度数之比为( )
A.3:4:5 B. 1:2:3
C. 5:4:3 D. 3:2:1
13.如图,若AB∥CD,EF与AB、CD分别相交于E、 F,PE⊥EF, ∠EFD的平分线与EP交于P,且BEP=40°,则∠EPF= ;
65°
综合训练
D
14.如图, 在△ABC中, BD、CE分别平分∠ABC和∠ACB.
(1).若∠A=60°,求∠BOC的度数.
(2).若∠A=α,求∠BOC的度数.
(1)解:∵BD、CE分别平分∠ABC和∠ACB
∴∠DBC= ∠ABC ,∠ECB = ∠ACB
又∵∠ABC+ ∠ACB =1800- ∠A= 1800- 600=1200 ∴∠BOC= 1800- (∠ABC + ∠ACB )
=1800- ×1200=1200
(2)解:由(1)知∠ABC+ ∠ACB =1800- ∠A
∠BOC= 1800- (∠ABC + ∠ACB )
=1800- (1800- ∠A)=900+ ∠A
15.如图, 在△ABC中, 延长BC至D, BE、CE分别平分∠ABC和∠ACD.
(1).若∠A=80°,求∠E的度数.
(2).根据(1)猜测∠E 与∠A的关系,并说明理由.
细观察 多思考
解∵ ∠C=∠ABC=2∠A
∠A +∠ABC+∠C= 180°
∴ 5∠A = 180°
∴ ∠A = 36°
∴ ∠C= 72°
∵BD是AC边上的高,
∴ ∠DBC= 180°- 90°- 72°=18°
解∵AD是△ABC的高, ∠C= 70°
∴ ∠DAC= 180°- 90°- 70°= 20°
∵ ∠BAC= 50°
∴ ∠ABC= 180°- 50°- 70°= 60°
∵ AE 和BF是角平分线
∴ ∠BAO=25°, ∠ABO=30°
∴ ∠AOB= 180°- 25°- 30°= 125°
7.如图, △ABC中, ∠A= ∠ABD,
∠C= ∠BDC= ∠ABC,求∠DBC的度数
A
B
C
D
·例题精讲
1.如图△ABO与△CDO称为“对顶三角形”,你能证明∠A+ ∠B= ∠C+ ∠D吗?
2.如图2,DM,BM是∠D ,∠B的平分线,求证2∠M= ∠C+ ∠A
3.∠CAD+ ∠B+ ∠C+ ∠D+ ∠E=( )
2.如图,则ABC的形状是( ) A、锐角三角形 B、钝角三角形
C、直角三角形 D、等腰三角形
3.如图, ∠A+∠B+∠C+∠D+∠E+∠F= ;
C
360°
巩固练习
1.三角形两边长分别为2cm,6cm,且周长是奇数,则第三边长是 ( )
5cm,或7cm
数学思想: 整体思想和转化思想
在一个图形中同时出现两条角平分线时,常常要用到整体思想.
运用转化思想将复杂的问题转化为简单的问题,将未知的问题转化为已知的问题,是常用的数学方法.
作业:
1.如图, △ABC中, ∠A= ∠ABD,
∠C= ∠BDC= ∠ABC,求∠DBC的度数
A
B
C
D
2、求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
A
G
F
E
D
C
B
第七章三角形
复 习
(n-2) ×180°
三角形
与三角形有关的线段
a-b<c<a+b(a-b>0)
高
三角形的边
三角形的判定定理
中线
角平分线的定义
位置、交点
三角形的内角和
多边形的内角和
多边形的外角和
三角形的外角和
多边形外角和为360°
镶嵌的原理
本章知识结构
三角形的角
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形
A
C
B
1.AB、BC、CA叫做三角形的边
2.点A、B、C叫做三角形的顶点
3.∠ A、 ∠ B、 ∠ C叫做三角形的内角,简称三角形的角。
一、与三角形有关的线段
1、三角形的定义:
观察
按角分:
直角三角形
锐角三角形
钝角三角形
2.三角形的分类
三角形
直角三角形
锐角三角形
钝角三角形
再观察
等边三角形
等腰三角形
不等边三角形
2.三角形的分类
腰
腰
底
顶角
底角
底角
1. 三角形的三边关系:
(1)三角形的任何两边之和大于第三边:
(2)三角形的任何两边之差小于第三边
(3)判断三条已知线段a、b、c能否组成三角形;
当a最长,且有b+c>a时,就可构成三角形。
(4)确定三角形第三边的取值范围:
两边之差<第三边<两边之和。
2. 三角形的三条高线(或高线所在的直线)交于一点,
锐角三角形三条高线交于三角形内部一点,
直角三角形三条高线交于直角顶点,
钝角三角形三条高线所在的直线交于三角形外部一点。
3. 三角形的三条中线交于三角形内部一点。
4. 三角形的三条角平分线交于三角形内部一点。
1、三角形两条边分别是2cm,7cm,则第三边c的范围为 。
2、等腰三角形的一边长为6cm,另一边长为12cm,则其周长( )
A、24cm B、30cm
C、24cM或30cm D、18cm
3、用7根火柴首尾顺次连结摆成一个三角形,能摆成不同的三角形的个数为 。
5(cm)<c<9(cm)
B
2
(3,3,1;2,2,3)
1、等腰三角形一边的长是
另一边的长是8,则它的周
长是 。
18或21
19
5
3
填一填
2、一个三角形的两边长分别是 和 ,第三边的长为奇数,则第三边的长为_____ .
4、同上题图,若
△ACD的面积为
,则△ABC
的面积为 .
3、如图,已知:AD是△ABC
的中线,△ABC的面积为 ,则△ABD的面积是 .
A
B
C
D
50cm2
25cm2
80cm2
40cm2
60cm2
120cm2
30cm2
60cm2
填一填
5. 三角形具有稳定性,而四边形没有稳定性。
6. 三角形的内角
三角形内角和定理:三角形的三个内角和为
推论:直角三角形的两个锐角互余。
7. 三角形的外角:
定义:三角形一边与另一边的延长线组成的角叫做三角形的外角。
性质:1.三角形的一个外角等于与它不相邻的两个内角的和。
2.三角形的一个外角大于与它不相邻的任何一个内角。
3.三角形的一个外角与它相邻的内角互为邻补角。
8. 三角形的外角和:三角形的三个外角和为
5、如图,在△ABC中,CE,BF是两条高,若∠A= ,∠BCE= ,则∠EBF的度数是 ,
∠FBC的度
数是 .
25°
20°
40°
30°
50°
65°
25°
40°
20°
70°
40°
A
B
C
E
F
填一填
6、如图, 分别是△ABC的高和角平线, , 则 =______度.
7、如图 , 平分 ,交AB于E,
则 =______ 度.
看你会不会
题型考查
3、如图,CD是Rt△ABC斜边上的高,与∠A相等的角是 ,理由是 。
A
B
C
D
题型考查
4、如图,在△ABC中,两条角平分线BD和CE相交于点O,若∠BOC=116°,那么∠A的度数是 。
A
B
C
D
E
O
1∶2∶3
2∶3∶4
①∠A=380,∠B=730 , ∠C=
③∠B=400,∠A∶∠C=3∶4
∠C=
8、若三角形三个内角的度数
之比为 ,则这三个内角的度数分别是_______________.
1∶3∶6
180、540、1080
300、600、900
400、600、800
9、在△ABC中,根据下列条件,求∠C的度数.
690
②AB⊥BC,∠A=350 ∠C=
550
800
填一填
5、三角形中至少有一个角大于或等于( )
A、45° B、55° C、60° D、65°
6、如果直角三角形的一个锐角是另一个锐角的4倍,那么这个直角三角形中一个锐角的度数是( )
A、9° B、18° C、27° D、36°
题型考查
4.下列能说明∠1>∠2的是( )
A
B
D
C
1.符合条件∠A+∠B=62°的三角形是( )
A、4㎝ B、5㎝ C、9㎝ D、14㎝
C
3.如图,在△ABC中,∠A=70° ∠B=60°,点D在BC的延长线上,则 ∠ACD=____度.
130
A
B
C
D
2.在下列长度的四根木棒中,能与4㎝,9㎝两根木棒围成三角形的是( )
A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定
C
题型考查
n-3
n-2
1
2
3
2
3
4
2
5
9
n-3
n-2
3×1800
4×1800
(n-2)×1800
1
2
3
2
3
4
2×1800
3600
3600
3600
3600
1、记住以下角度:
(1)三角形的内角和为______;
180°
四边形的内角和为______;
360°
五边形的内角和为______;
540°
六边形的内角和为______;
720°
(2)正三角形的每个内角为______;
60°
正四边形的每个内角为______;
90°
正五边形的每个内角为______;
108°
正六边形的每个内角为______;
120°
10 、一个多边形的每一个外角都等于 ,则该多边形的内角和等于_____ 度.
11、下列边长为a的正多边形与边长为a的正方形组合起来(1)正三角形 (2)正五边形 (3)正六边形 (4)正八边形, 其中不能镶嵌成平面的是( )
A. (1) (2) B. (2) (3) C. (1) (3) D. (1) (4)
填一填
1440
D
5.如图所示:△ABC中,D,E分别为BC,AD的中点,且S △ABC=4,则S阴为_____
基础过关
A
F
E
D
B
C
O
6.如图所示:△ABC中,AD⊥BC于D, BE⊥AC于E, CF⊥AB于F,则△OBC的高是 。OF是哪些三角形的高?
OD
△OAB, △OAF, △OBF
1
7. 如图,则ABC的形状是( ) A、锐角三角形 B、钝角三角形
C、直角三角形 D、等腰三角形
8.如图, ∠A+∠B+∠C+∠D+∠E+∠F= ;
C
360°
基础过关
10.AB∥CD, ∠A=45°∠C=80°,则∠M=
11.如图,直线DE与△ABC的三边所在直线交与D、E、F,A=40°,D=25°,DE⊥AB,则∠ ACB=
基础过关
9、如果一个三角形的各内角与一个外角的
和是225°,则与这个外角相邻的内角是____度.
1350
350
750
12.若一个三角形的三个外角度数之比为3:4:5,则与之相邻的三个内角度数之比为( )
A.3:4:5 B. 1:2:3
C. 5:4:3 D. 3:2:1
13.如图,若AB∥CD,EF与AB、CD分别相交于E、 F,PE⊥EF, ∠EFD的平分线与EP交于P,且BEP=40°,则∠EPF= ;
65°
综合训练
D
14.如图, 在△ABC中, BD、CE分别平分∠ABC和∠ACB.
(1).若∠A=60°,求∠BOC的度数.
(2).若∠A=α,求∠BOC的度数.
(1)解:∵BD、CE分别平分∠ABC和∠ACB
∴∠DBC= ∠ABC ,∠ECB = ∠ACB
又∵∠ABC+ ∠ACB =1800- ∠A= 1800- 600=1200 ∴∠BOC= 1800- (∠ABC + ∠ACB )
=1800- ×1200=1200
(2)解:由(1)知∠ABC+ ∠ACB =1800- ∠A
∠BOC= 1800- (∠ABC + ∠ACB )
=1800- (1800- ∠A)=900+ ∠A
15.如图, 在△ABC中, 延长BC至D, BE、CE分别平分∠ABC和∠ACD.
(1).若∠A=80°,求∠E的度数.
(2).根据(1)猜测∠E 与∠A的关系,并说明理由.
细观察 多思考
解∵ ∠C=∠ABC=2∠A
∠A +∠ABC+∠C= 180°
∴ 5∠A = 180°
∴ ∠A = 36°
∴ ∠C= 72°
∵BD是AC边上的高,
∴ ∠DBC= 180°- 90°- 72°=18°
解∵AD是△ABC的高, ∠C= 70°
∴ ∠DAC= 180°- 90°- 70°= 20°
∵ ∠BAC= 50°
∴ ∠ABC= 180°- 50°- 70°= 60°
∵ AE 和BF是角平分线
∴ ∠BAO=25°, ∠ABO=30°
∴ ∠AOB= 180°- 25°- 30°= 125°
7.如图, △ABC中, ∠A= ∠ABD,
∠C= ∠BDC= ∠ABC,求∠DBC的度数
A
B
C
D
·例题精讲
1.如图△ABO与△CDO称为“对顶三角形”,你能证明∠A+ ∠B= ∠C+ ∠D吗?
2.如图2,DM,BM是∠D ,∠B的平分线,求证2∠M= ∠C+ ∠A
3.∠CAD+ ∠B+ ∠C+ ∠D+ ∠E=( )
2.如图,则ABC的形状是( ) A、锐角三角形 B、钝角三角形
C、直角三角形 D、等腰三角形
3.如图, ∠A+∠B+∠C+∠D+∠E+∠F= ;
C
360°
巩固练习
1.三角形两边长分别为2cm,6cm,且周长是奇数,则第三边长是 ( )
5cm,或7cm
数学思想: 整体思想和转化思想
在一个图形中同时出现两条角平分线时,常常要用到整体思想.
运用转化思想将复杂的问题转化为简单的问题,将未知的问题转化为已知的问题,是常用的数学方法.
作业:
1.如图, △ABC中, ∠A= ∠ABD,
∠C= ∠BDC= ∠ABC,求∠DBC的度数
A
B
C
D
2、求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
A
G
F
E
D
C
B
