勾股定理(复习)
图片预览


文档简介
(共14张PPT)
通过本章复习使学生熟练掌握勾股定理及其逆定理;能熟练
运用知识解决实际问题;能够熟练运用勾股定理的逆定理判定直
角三角形,再次提高学生对“数形结合”思想的运用与理解;掌握
命题及互逆命题的定义.
掌握勾股定理及其逆定理.
理解勾股定理及其逆定理的应用.
勾定理及逆定理的理解.
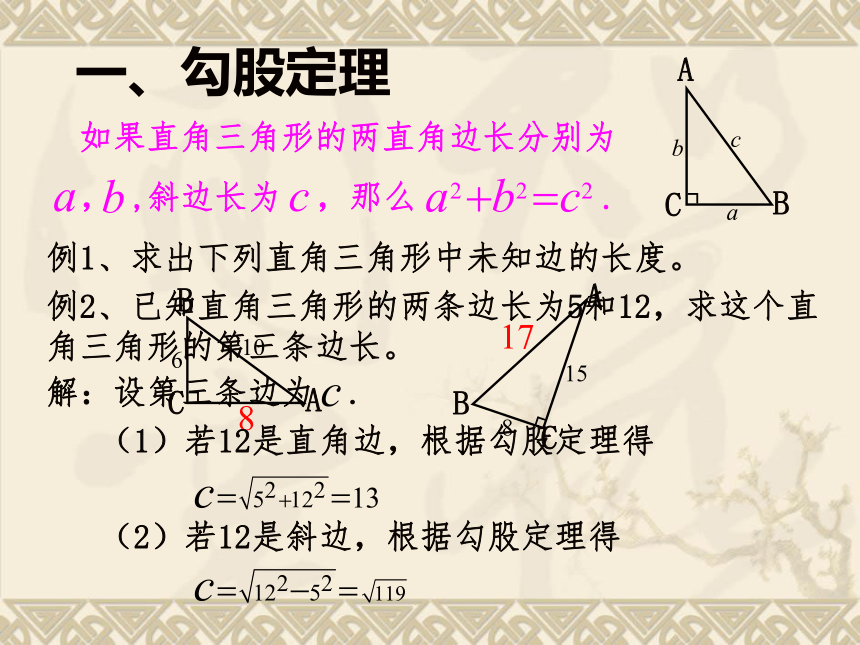
一、勾股定理
A
B
C
A
B
C
A
B
C
例1、求出下列直角三角形中未知边的长度。
例2、已知直角三角形的两条边长为5和12,求这个直角三角形的第三条边长。
解:设第三条边为 .
(1)若12是直角边,根据勾股定理得
(2)若12是斜边,根据勾股定理得
如果直角三角形的两直角边长分别为
, ,斜边长为 ,那么 .
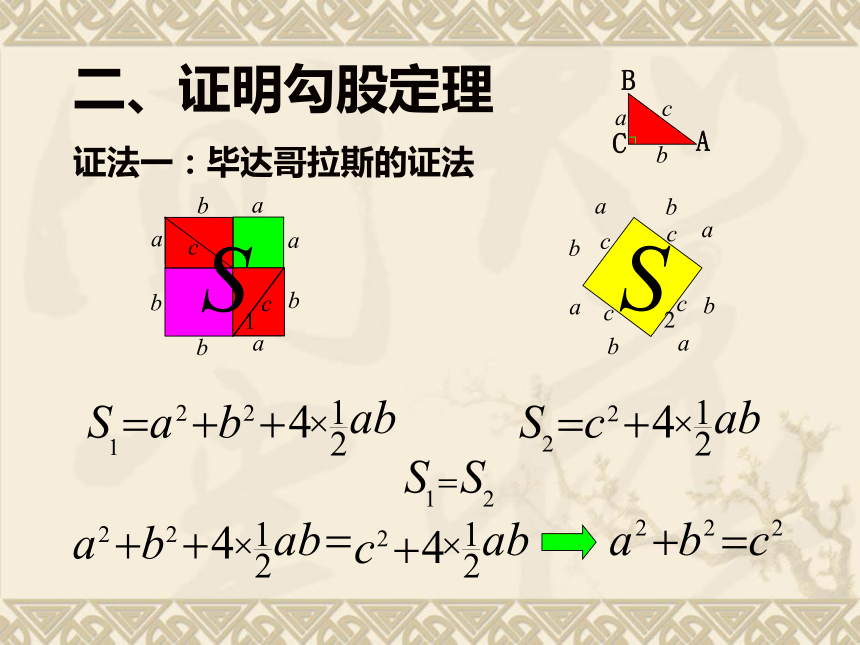
二、证明勾股定理
证法一:毕达哥拉斯的证法
A
B
C
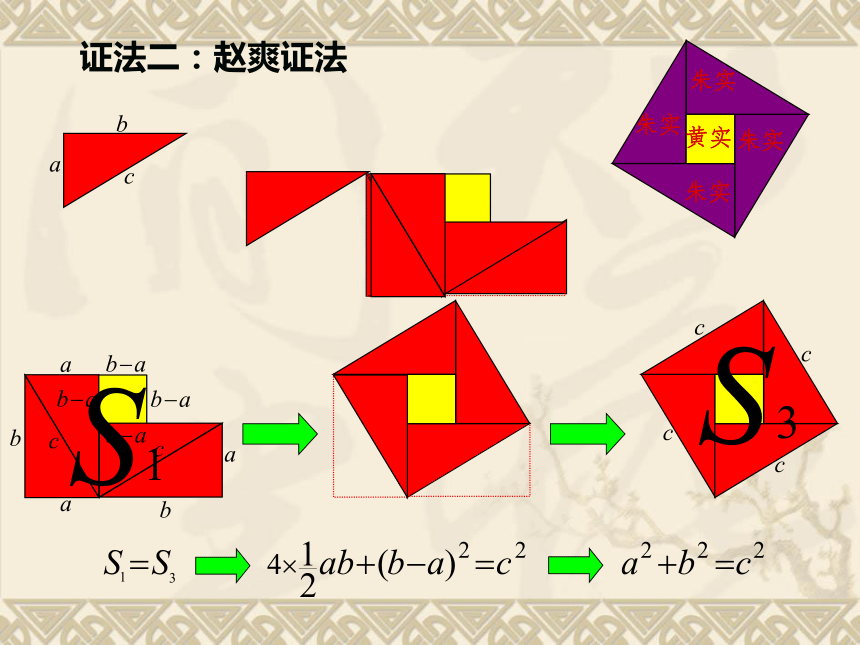
证法二:赵爽证法
朱实
朱实
朱实
朱实
黄实
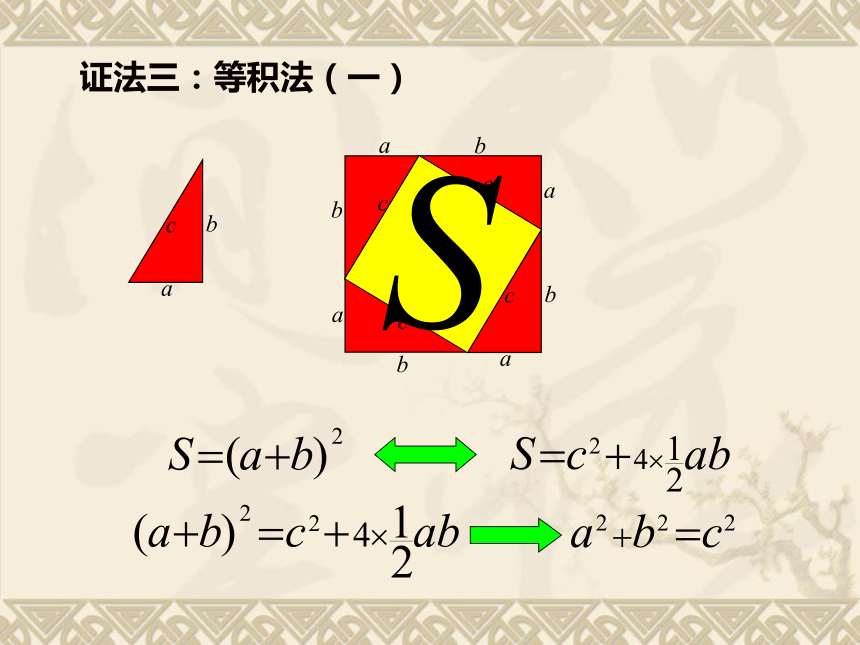
证法三:等积法(一)
证法四:等积法(二)
三、勾股定理的逆定理
如果三角形的三边长 、 、 满足 ,
那么这个三角形是直角三角形。
例3、以下列三条线段为边的△ABC是否是直角三角形?
(1) ; ;
(2) ; ;
解:∵
∴△ABC不是直角三角形。
∴
∴
∴△ABC是直角三角形。
解:∵
例4、试证明以 、 、 ( )为边的三角形是直角三角形。
1
n
>
证明:∵
1
n
>
∴ ;
∵
∴以 、 、 ( )为边的三角形是直角三角形。
1
n
>
例5、下列三个数是否是勾股数?
(1) ; ; .( )
(2) ; ; .( )
(3) ; ; .( )
(5) ; ; .( )
(6) ; ; .( )
(4) ; ; .( )
15
能够成为直角三角形三条边长的三个正整数,叫做勾股弦数(勾股数)
组成的三角形是直角三角形
;
;
( )
例6、如果 ; ;( )是一组勾股数,那么
; ; (m是正整数)也是一组勾股数吗?再举
出几组勾股数?
解:∵
∴
∴ ; ; 也是一组勾股数。
不是
不是
不是
是
是
是
四、互逆命题及互逆定理
两个命题,如果命题1的题设是命题2的结论,命题1的结论是命题2的题设,那么这两个命互为逆命题。把其中一个叫做原命题,那么另一个叫做它的逆命题。
如果一个定理的逆命题经过证明是正确的,那么它也是一定理,这两个定理互为逆定理。
例7、说出下列命题的逆命题,这些命题的逆命题成立吗?
(1)对顶角相等。
(2)如果两个实数相等,那么它们的绝对值相等。
(3)全等三角形的对应边相等。
(4)全等三角形的对应角相等。
相等的角是对顶角。( )
如果两个实数的绝对值相等,那么它们相等。( )
对应边相等的三角形全等。( )
对应角相等的三角形全等。( )
不成立
不成立
成立
不成立
例8、如图所示,公路MN和公路EF在E点处交会,点A处有一所中学,AE=160m,点A到公路MN的距离为80m,假设拖拉机行驶时周围100m以内会受到噪声影响,那么拖拉机在公路MN上沿EN方向行驶时,学校是否会受到影响?请说明理由;如果受影响,已知拖拉机的速度为18km/h,那么学校受影响的时间为多少秒?
M
N
E
A
F
·
解:因为点A到MN的距离为80m,而拖拉机行驶时噪声范围为100m,所以拖拉机会影响学校。
B
C
D
80m
100m
100m
假设B、C为公路MN上的两点,拖拉机行驶在BC段时,学校会受到噪声的影响。如图。
在Rt△ABD中,根据勾股定理有
(m)
∴BC=2BD=2×60=120(m)
∴t=BC÷(18000 ÷3600)=120 ÷5=24(s)
所以学校受影响的时间为24s.
通过本章复习使学生熟练掌握勾股定理及其逆定理;能熟练
运用知识解决实际问题;能够熟练运用勾股定理的逆定理判定直
角三角形,再次提高学生对“数形结合”思想的运用与理解;掌握
命题及互逆命题的定义.
掌握勾股定理及其逆定理.
理解勾股定理及其逆定理的应用.
勾定理及逆定理的理解.
一、勾股定理
A
B
C
A
B
C
A
B
C
例1、求出下列直角三角形中未知边的长度。
例2、已知直角三角形的两条边长为5和12,求这个直角三角形的第三条边长。
解:设第三条边为 .
(1)若12是直角边,根据勾股定理得
(2)若12是斜边,根据勾股定理得
如果直角三角形的两直角边长分别为
, ,斜边长为 ,那么 .
二、证明勾股定理
证法一:毕达哥拉斯的证法
A
B
C
证法二:赵爽证法
朱实
朱实
朱实
朱实
黄实
证法三:等积法(一)
证法四:等积法(二)
三、勾股定理的逆定理
如果三角形的三边长 、 、 满足 ,
那么这个三角形是直角三角形。
例3、以下列三条线段为边的△ABC是否是直角三角形?
(1) ; ;
(2) ; ;
解:∵
∴△ABC不是直角三角形。
∴
∴
∴△ABC是直角三角形。
解:∵
例4、试证明以 、 、 ( )为边的三角形是直角三角形。
1
n
>
证明:∵
1
n
>
∴ ;
∵
∴以 、 、 ( )为边的三角形是直角三角形。
1
n
>
例5、下列三个数是否是勾股数?
(1) ; ; .( )
(2) ; ; .( )
(3) ; ; .( )
(5) ; ; .( )
(6) ; ; .( )
(4) ; ; .( )
15
能够成为直角三角形三条边长的三个正整数,叫做勾股弦数(勾股数)
组成的三角形是直角三角形
;
;
( )
例6、如果 ; ;( )是一组勾股数,那么
; ; (m是正整数)也是一组勾股数吗?再举
出几组勾股数?
解:∵
∴
∴ ; ; 也是一组勾股数。
不是
不是
不是
是
是
是
四、互逆命题及互逆定理
两个命题,如果命题1的题设是命题2的结论,命题1的结论是命题2的题设,那么这两个命互为逆命题。把其中一个叫做原命题,那么另一个叫做它的逆命题。
如果一个定理的逆命题经过证明是正确的,那么它也是一定理,这两个定理互为逆定理。
例7、说出下列命题的逆命题,这些命题的逆命题成立吗?
(1)对顶角相等。
(2)如果两个实数相等,那么它们的绝对值相等。
(3)全等三角形的对应边相等。
(4)全等三角形的对应角相等。
相等的角是对顶角。( )
如果两个实数的绝对值相等,那么它们相等。( )
对应边相等的三角形全等。( )
对应角相等的三角形全等。( )
不成立
不成立
成立
不成立
例8、如图所示,公路MN和公路EF在E点处交会,点A处有一所中学,AE=160m,点A到公路MN的距离为80m,假设拖拉机行驶时周围100m以内会受到噪声影响,那么拖拉机在公路MN上沿EN方向行驶时,学校是否会受到影响?请说明理由;如果受影响,已知拖拉机的速度为18km/h,那么学校受影响的时间为多少秒?
M
N
E
A
F
·
解:因为点A到MN的距离为80m,而拖拉机行驶时噪声范围为100m,所以拖拉机会影响学校。
B
C
D
80m
100m
100m
假设B、C为公路MN上的两点,拖拉机行驶在BC段时,学校会受到噪声的影响。如图。
在Rt△ABD中,根据勾股定理有
(m)
∴BC=2BD=2×60=120(m)
∴t=BC÷(18000 ÷3600)=120 ÷5=24(s)
所以学校受影响的时间为24s.
