2020—2021学年北师大版数学七年级下册 6.2 频率的稳定性 教学课件(27张)
文档属性
| 名称 | 2020—2021学年北师大版数学七年级下册 6.2 频率的稳定性 教学课件(27张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-16 20:06:56 | ||
图片预览







文档简介
(共27张PPT)
第六章
频率与概率
2
频率的稳定性
知识点一:频率的稳定性
掷一枚图钉,落地后会出现两种情况:
你认为钉尖朝上和钉尖朝下的可能性一样大吗?
试验总次数
钉尖朝上的次数
钉尖朝下的次数
钉尖朝上的频率
钉尖朝下的频率
在n次重复试验中,事件A发生了m次,则比值
称为事件A发生的频率.
(1)两人一组做20次掷图钉的游戏,并将数据记录在下表中:
(2)累计全班同学的实验结果,并将试验数据汇总填入下表:
试验总次数n
20
40
80
120
160
200
240
280
320
360
400
钉尖朝上次数m
钉尖朝上频率
20
40
80
120
200
240
160
320
280
0.2
400
360
1.0
0.6
0.8
0.4
钉尖朝上的频率
试验总次数
(3)根据上表完成下面的折线统计图:
20
40
80
120
200
240
160
320
280
0.2
400
360
1.0
0.6
0.8
0.4
钉尖朝上的频率
试验总次数
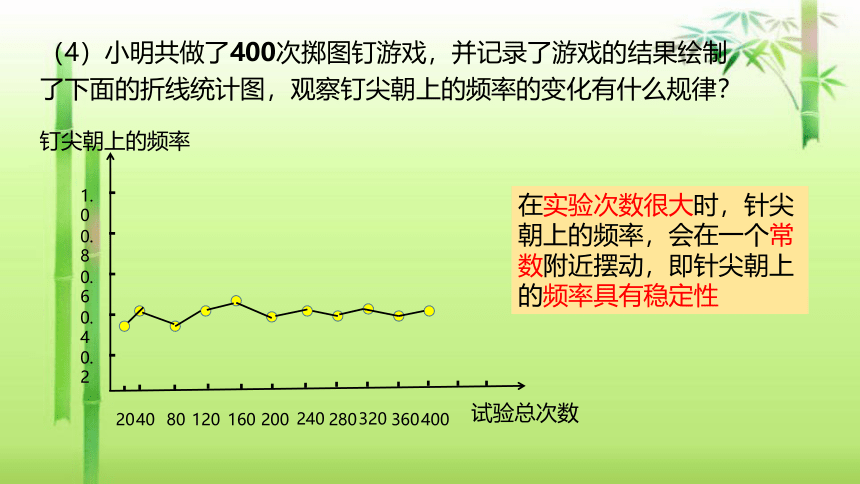
(4)小明共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,观察钉尖朝上的频率的变化有什么规律?
在实验次数很大时,针尖朝上的频率,会在一个常数附近摆动,即针尖朝上的频率具有稳定性
议一议
(1)通过上面的试验,你认为钉尖朝上和钉尖
朝下的可能性一样大吗?你是怎样想的?
(2)小军和小凡一起做了1000次掷图钉的试验,
其中有640次钉尖朝上.据此,他们认为钉尖朝上的可能性比钉尖朝下的可能性大.
你同意他们的说法吗?
根据频率的稳定性,在实验次数很大(1000次)情况下,有理由这么认为
例1
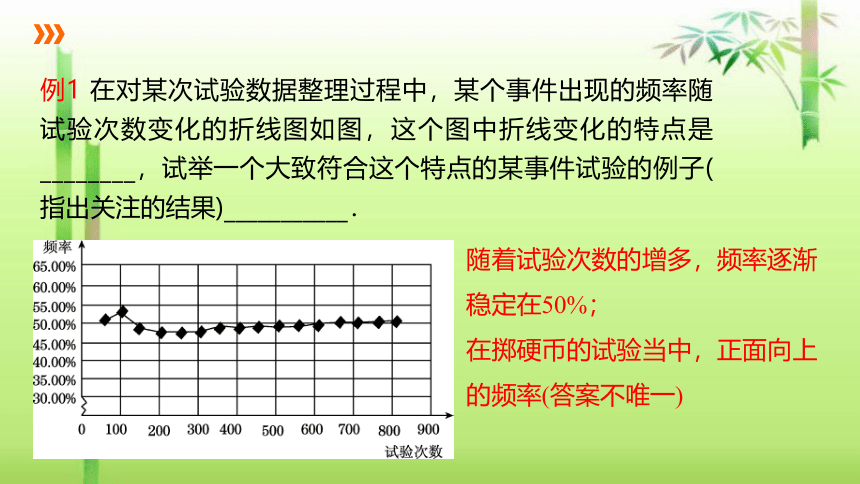
在对某次试验数据整理过程中,某个事件出现的频率随试验次数变化的折线图如图,这个图中折线变化的特点是________,试举一个大致符合这个特点的某事件试验的例子(指出关注的结果)___________.
随着试验次数的增多,频率逐渐稳定在50%;
在掷硬币的试验当中,正面向上的频率(答案不唯一)
知识点二:频率与概率的关系
掷一枚质地均匀的硬币,硬币落下后,会出现两种情况:
你认为正面朝上和正面朝下的可能性相同吗?
做一做
(1)同桌两人做20次掷硬币的游戏,并将数据记录在下表中:
试验总次数
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
(2)累计全班同学的试验结果,并将试验数据汇总填人下表:
试验总次数
20
40
60
80
100
120
140
160
180
200
正面朝上的次数
正面朝上的频率
正面朝下的次数
正面朝下的频率
(3)根据上表,完成下面的折线统计图:
(4)观察上面的折线统计图,你发现了什么规律?
当抛掷硬币的次数很大时,正面朝上的频率都会在一个常数0.5附近摆动,即硬币正面朝上的频率具有稳定性.
试验者
试验总
次数n
正面朝上
的次数m
正面朝上
的频率
布丰
4
040
2
048
0.506
9
德·摩根
4
092
2
048
0.500
5
费勒
10
000
4
979
0.497
9
皮尔逊
12
000
6
019
0.501
6
皮尔逊
24
000
12
012
0.500
5
维尼
30
000
14
994
0.499
8
罗曼诺夫斯基
80
640
39
699
0.492
3
(5)下表列出了一些历史上的数学家所做的抛硬币试验的数据:
分析试验结果及上面数学家大量重复试验数据,
大家有何发现?
试验次数越多频率越接近0.5.
抛掷次数n
0.5
2048
4040
10000
12000
24000
“正面向上”
频率
无论是掷质地均匀的硬币还是掷图钉,在试验次数很大时正面朝上(钉尖朝上)的频率都会在一个常数附近摆动,这就是频率的稳定性.
由于事件A发生的频率,表示该事件发生的频繁程度,频率越大,事件A发生越频繁,这就意味着事件A发生的可能性也越大,因而,我们就用这个常数来表示事件A发生的可能性的大小.我们把刻画事件A发生的可能性大小的数值,称为事件A发生的概率,记为P
(A).
概率的意义:
事件发生的可能性的大小
概率的数值:
为频率的稳定值(概率与频率的关系)
事件A发生的概率P(A)的取值范围是什么?必然事件、不可能事件以及随机事件发生的概率分别是多少?
必然事件发生的概率为1;
不可能事件发生的概率为0;
随机事件A发生的概率P(A)是0与1之间的一个常数
例2
瓷砖生产受烧制时间、温度、材质的影响,一块砖坯放在炉中烧制,可能成为合格品,也可能成为次品或废品,究竟发生那种结果,在烧制前无法预知,所以这是一种随机现象.而烧制的结果是“合格品”是一个随机事件,这个事件的概率称为“合格品率”.
由于烧制结果不是等可能的,我们常用“合格品”的频率作为“合格品率”的估计.
某瓷砖厂对最近出炉的一大批某型号瓷砖进行质量抽检,结果如下:
抽取瓷砖数n
100
200
300
400
500
600
800
1000
2000
合格品数m
95
192
287
385
481
577
770
961
1924
合格品率
(1)计算上表中合格品率的各频率(精确到0.001);
(2)估计这种瓷砖的合格品率(精确到0.01);
(3)若该厂本月生产该型号瓷砖500000块,试估计合格品数.
解:(1)逐项计算,填表如下:
抽取瓷砖数n
100
200
300
400
500
600
800
1000
2000
合格品数m
95
192
287
385
481
577
770
961
1924
合格品率
0.950
0.960
0.957
0.963
0.962
0.962
0.963
0.961
0.962
(2)观察上表,可以发现,当抽取的瓷砖数n≥400时,合格品率
稳定在0.962的附近,
所以我们可取P=0.96作为该型号瓷砖的合格品率的估计.
(3)500000×96%=480000(块),可以估计该型号合格品数为480000块.
1.小胡将一枚质地均匀的硬币抛掷了10次,正面朝
上的情况出现了6次,若用A表示正面朝上这一事件,
则事件A发生的( )
A.频率是0.4
B.频率是0.6
C.频率是6
D.频率接近0.6
B
2.
小明和同学做“抛掷质地均匀的硬币试验”获得的数据如下表所示:
抛掷次数
100
200
300
400
500
正面朝上的频数
53
98
156
202
244
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近( )
A.20
B.300
C.500
D.800
C
3.
小明练习射击,共射击600次,其中有380次击中靶子,由此可估计,小明射击一次击中靶子的概率是( )
A.38%
B.60%
C.63%
D.无法确定
C
4.一水塘里有鲤鱼、鲫鱼、鲢鱼共1
000尾,一渔民通过多次捕获实验后发现:鲤鱼、鲫鱼出现的频率是31%和42%,则这个水塘里有鲤鱼约
尾,鲢鱼约
尾.
310
270
5.连续抛掷一枚质地均匀的一元硬币100次出现了100次正面朝上,则第101次抛掷该硬币出现正面朝上的概率是 .
0.5
6.
扬州某毛绒玩具厂对一批毛绒玩具进行质量抽检的结果如下:
抽取的毛绒玩具数n
20
50
100
200
500
1000
1500
2000
优等品的频数m
19
47
91
184
462
921
1379
1846
优等品的频率
(精确到0.001)
0.950
0.940
0.910
0.920
0.924
0.921
0.919
0.923
从这批玩具中,任意抽取的一个毛绒玩具是优等品的概率的估计值是 .(精确到0.01)
0.92
1.频率的定义:在n次重复试验中,不确定事件A发生了m次,则比值
称为事件
A发生的频率.
注意:频率是一个比值,
没有单位.
2.频率的稳定性:
在大量重复试验的情况下,事件的频率会呈现稳定性,即频率在一个“常数”附近摆动.随着试验次数的增加,摆动的幅度将越来越小.
频率与概率的关系
联系:
频率
概率
事件发生的频繁程度
事件发生的
可能性大小
稳定性
大量重复试验
区别:
频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同;
概率是一个确定数,是客观存在的,与每次试验无关.
第六章
频率与概率
2
频率的稳定性
知识点一:频率的稳定性
掷一枚图钉,落地后会出现两种情况:
你认为钉尖朝上和钉尖朝下的可能性一样大吗?
试验总次数
钉尖朝上的次数
钉尖朝下的次数
钉尖朝上的频率
钉尖朝下的频率
在n次重复试验中,事件A发生了m次,则比值
称为事件A发生的频率.
(1)两人一组做20次掷图钉的游戏,并将数据记录在下表中:
(2)累计全班同学的实验结果,并将试验数据汇总填入下表:
试验总次数n
20
40
80
120
160
200
240
280
320
360
400
钉尖朝上次数m
钉尖朝上频率
20
40
80
120
200
240
160
320
280
0.2
400
360
1.0
0.6
0.8
0.4
钉尖朝上的频率
试验总次数
(3)根据上表完成下面的折线统计图:
20
40
80
120
200
240
160
320
280
0.2
400
360
1.0
0.6
0.8
0.4
钉尖朝上的频率
试验总次数
(4)小明共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,观察钉尖朝上的频率的变化有什么规律?
在实验次数很大时,针尖朝上的频率,会在一个常数附近摆动,即针尖朝上的频率具有稳定性
议一议
(1)通过上面的试验,你认为钉尖朝上和钉尖
朝下的可能性一样大吗?你是怎样想的?
(2)小军和小凡一起做了1000次掷图钉的试验,
其中有640次钉尖朝上.据此,他们认为钉尖朝上的可能性比钉尖朝下的可能性大.
你同意他们的说法吗?
根据频率的稳定性,在实验次数很大(1000次)情况下,有理由这么认为
例1
在对某次试验数据整理过程中,某个事件出现的频率随试验次数变化的折线图如图,这个图中折线变化的特点是________,试举一个大致符合这个特点的某事件试验的例子(指出关注的结果)___________.
随着试验次数的增多,频率逐渐稳定在50%;
在掷硬币的试验当中,正面向上的频率(答案不唯一)
知识点二:频率与概率的关系
掷一枚质地均匀的硬币,硬币落下后,会出现两种情况:
你认为正面朝上和正面朝下的可能性相同吗?
做一做
(1)同桌两人做20次掷硬币的游戏,并将数据记录在下表中:
试验总次数
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
(2)累计全班同学的试验结果,并将试验数据汇总填人下表:
试验总次数
20
40
60
80
100
120
140
160
180
200
正面朝上的次数
正面朝上的频率
正面朝下的次数
正面朝下的频率
(3)根据上表,完成下面的折线统计图:
(4)观察上面的折线统计图,你发现了什么规律?
当抛掷硬币的次数很大时,正面朝上的频率都会在一个常数0.5附近摆动,即硬币正面朝上的频率具有稳定性.
试验者
试验总
次数n
正面朝上
的次数m
正面朝上
的频率
布丰
4
040
2
048
0.506
9
德·摩根
4
092
2
048
0.500
5
费勒
10
000
4
979
0.497
9
皮尔逊
12
000
6
019
0.501
6
皮尔逊
24
000
12
012
0.500
5
维尼
30
000
14
994
0.499
8
罗曼诺夫斯基
80
640
39
699
0.492
3
(5)下表列出了一些历史上的数学家所做的抛硬币试验的数据:
分析试验结果及上面数学家大量重复试验数据,
大家有何发现?
试验次数越多频率越接近0.5.
抛掷次数n
0.5
2048
4040
10000
12000
24000
“正面向上”
频率
无论是掷质地均匀的硬币还是掷图钉,在试验次数很大时正面朝上(钉尖朝上)的频率都会在一个常数附近摆动,这就是频率的稳定性.
由于事件A发生的频率,表示该事件发生的频繁程度,频率越大,事件A发生越频繁,这就意味着事件A发生的可能性也越大,因而,我们就用这个常数来表示事件A发生的可能性的大小.我们把刻画事件A发生的可能性大小的数值,称为事件A发生的概率,记为P
(A).
概率的意义:
事件发生的可能性的大小
概率的数值:
为频率的稳定值(概率与频率的关系)
事件A发生的概率P(A)的取值范围是什么?必然事件、不可能事件以及随机事件发生的概率分别是多少?
必然事件发生的概率为1;
不可能事件发生的概率为0;
随机事件A发生的概率P(A)是0与1之间的一个常数
例2
瓷砖生产受烧制时间、温度、材质的影响,一块砖坯放在炉中烧制,可能成为合格品,也可能成为次品或废品,究竟发生那种结果,在烧制前无法预知,所以这是一种随机现象.而烧制的结果是“合格品”是一个随机事件,这个事件的概率称为“合格品率”.
由于烧制结果不是等可能的,我们常用“合格品”的频率作为“合格品率”的估计.
某瓷砖厂对最近出炉的一大批某型号瓷砖进行质量抽检,结果如下:
抽取瓷砖数n
100
200
300
400
500
600
800
1000
2000
合格品数m
95
192
287
385
481
577
770
961
1924
合格品率
(1)计算上表中合格品率的各频率(精确到0.001);
(2)估计这种瓷砖的合格品率(精确到0.01);
(3)若该厂本月生产该型号瓷砖500000块,试估计合格品数.
解:(1)逐项计算,填表如下:
抽取瓷砖数n
100
200
300
400
500
600
800
1000
2000
合格品数m
95
192
287
385
481
577
770
961
1924
合格品率
0.950
0.960
0.957
0.963
0.962
0.962
0.963
0.961
0.962
(2)观察上表,可以发现,当抽取的瓷砖数n≥400时,合格品率
稳定在0.962的附近,
所以我们可取P=0.96作为该型号瓷砖的合格品率的估计.
(3)500000×96%=480000(块),可以估计该型号合格品数为480000块.
1.小胡将一枚质地均匀的硬币抛掷了10次,正面朝
上的情况出现了6次,若用A表示正面朝上这一事件,
则事件A发生的( )
A.频率是0.4
B.频率是0.6
C.频率是6
D.频率接近0.6
B
2.
小明和同学做“抛掷质地均匀的硬币试验”获得的数据如下表所示:
抛掷次数
100
200
300
400
500
正面朝上的频数
53
98
156
202
244
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近( )
A.20
B.300
C.500
D.800
C
3.
小明练习射击,共射击600次,其中有380次击中靶子,由此可估计,小明射击一次击中靶子的概率是( )
A.38%
B.60%
C.63%
D.无法确定
C
4.一水塘里有鲤鱼、鲫鱼、鲢鱼共1
000尾,一渔民通过多次捕获实验后发现:鲤鱼、鲫鱼出现的频率是31%和42%,则这个水塘里有鲤鱼约
尾,鲢鱼约
尾.
310
270
5.连续抛掷一枚质地均匀的一元硬币100次出现了100次正面朝上,则第101次抛掷该硬币出现正面朝上的概率是 .
0.5
6.
扬州某毛绒玩具厂对一批毛绒玩具进行质量抽检的结果如下:
抽取的毛绒玩具数n
20
50
100
200
500
1000
1500
2000
优等品的频数m
19
47
91
184
462
921
1379
1846
优等品的频率
(精确到0.001)
0.950
0.940
0.910
0.920
0.924
0.921
0.919
0.923
从这批玩具中,任意抽取的一个毛绒玩具是优等品的概率的估计值是 .(精确到0.01)
0.92
1.频率的定义:在n次重复试验中,不确定事件A发生了m次,则比值
称为事件
A发生的频率.
注意:频率是一个比值,
没有单位.
2.频率的稳定性:
在大量重复试验的情况下,事件的频率会呈现稳定性,即频率在一个“常数”附近摆动.随着试验次数的增加,摆动的幅度将越来越小.
频率与概率的关系
联系:
频率
概率
事件发生的频繁程度
事件发生的
可能性大小
稳定性
大量重复试验
区别:
频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同;
概率是一个确定数,是客观存在的,与每次试验无关.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
