上海市十校2012届高三下学期第二次联考 数学理
文档属性
| 名称 | 上海市十校2012届高三下学期第二次联考 数学理 |  | |
| 格式 | zip | ||
| 文件大小 | 444.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-21 18:22:54 | ||
图片预览



文档简介
上海市十校
2011—2012学年度高三第二学期考试
数 学 试 题(理)
一、填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.
1.若函数的反函数为,则 .
2.若复数是纯虚数(i是虚数单位,b为实数),则_________.
3.已知不等式的解集为,则实数的值为__________.
4.已知线性方程组的增广矩阵为,若该线性方程组解为,则实数___.
5.若向量、满足,且与的夹角为,则=________.
6.已知圆锥的母线长为,侧面积为,则此圆锥的体积为__________.
7.在中,已知,则 .
8.已知直线的参数方程是,则在轴上的截距为________.
9.若实数、{,, ,,},且,则方程表示焦点在轴上的双曲线的概率是__________.
10.已知是奇函数, 则的值域为 .
11.数列中,,对于任意,都有,Sn是的前n项和,则________.
12.已知双曲线的两个焦点分别为,该双曲线与抛物线有一个公共的焦点,且两曲线的一个交点为,,则的大小为______.(结果用反三角函数表示)
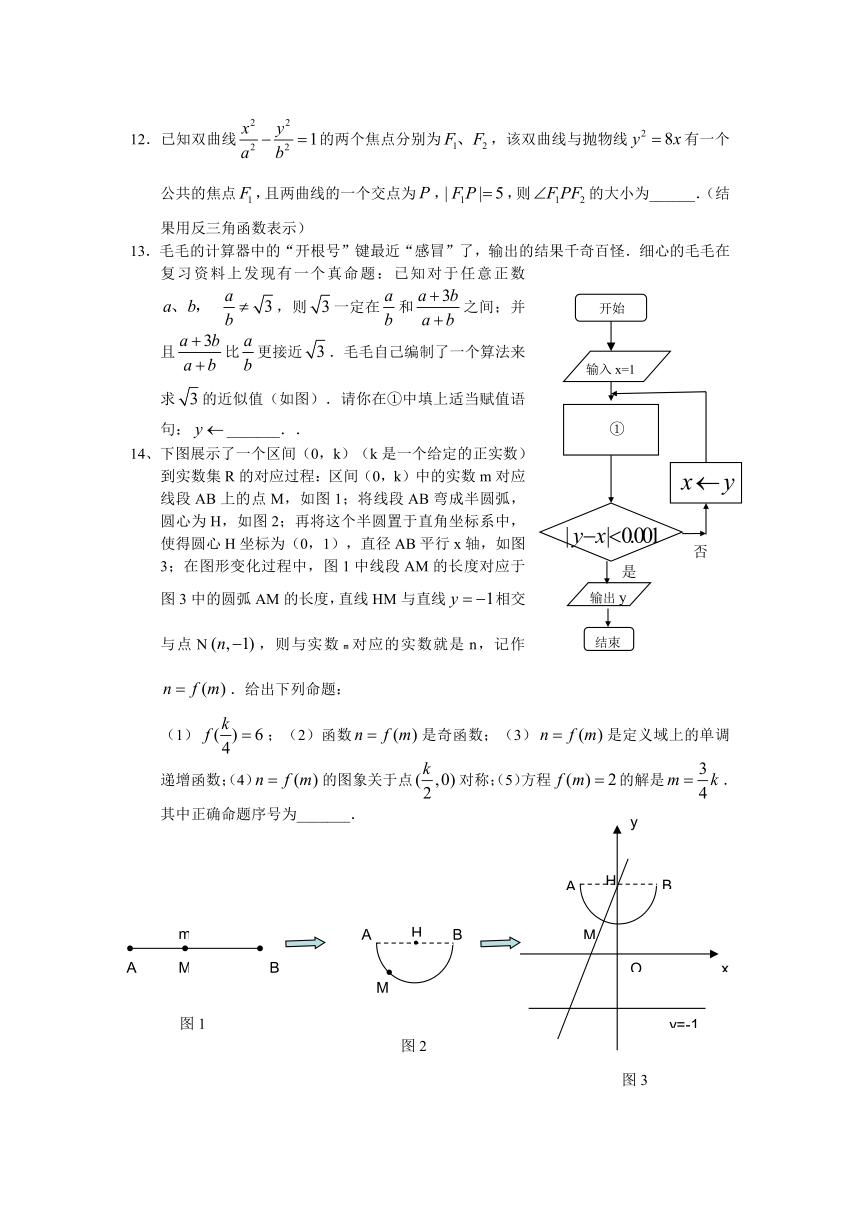
13.毛毛的计算器中的“开根号”键最近“感冒”了,输出的结果千奇百怪.细心的毛毛在复习资料上发现有一个真命题:已知对于任意正数,则一定在和之间;并且比更接近.毛毛自己编制了一个算法来求的近似值(如图).请你在①中填上适当赋值语句:_______..
14、下图展示了一个区间(0,k)(k是一个给定的正实数)到实数集R的对应过程:区间(0,k)中的实数m对应线段AB上的点M,如图1;将线段AB弯成半圆弧,圆心为H,如图2;再将这个半圆置于直角坐标系中,使得圆心H坐标为(0,1),直径AB平行x轴,如图3;在图形变化过程中,图1中线段AM的长度对应于图3中的圆弧AM的长度,直线HM与直线相交与点N,则与实数m对应的实数就是n,记作.给出下列命题:
(1);(2)函数是奇函数;(3)是定义域上的单调递增函数;(4)的图象关于点对称;(5)方程的解是.
其中正确命题序号为_______.
二、选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案.考生必须在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.
15.“”是“直线与直线平行”的 ( )
(A)充要条件 (B)充分不必要条件
(C)必要不充分条件 (D)既不充分也不必要条件
16.设事件A,B,已知=,=,=,则A,B之间的关系一定为( ).
(A) 互斥事件; (B)两个任意事件; (C)非互斥事件; (D)对立事件;
17.若为所在平面内一点,且满足,则ABC的形状为 ( )
(A)正三角形 (B)直角三角形 (C)等腰三角形 (D)等腰直角三角形
18.在平面直角坐标系中,设点,定义,其中O为坐标原点.对于下列结论:
(1)符合的点P的轨迹围成的图形的面积为2;
(2)设点P是直线:上任意一点,则;
(3)设点P是直线:上任意一点,则“使得最小的点P有无数个”的充要条件是“”;
(4)设点P是椭圆上任意一点,则.
其中正确的结论序号为 ( )
(A) (1)、(2) 、(3) (B) (1)、(3) 、(4)
(C) (2)、(3)、(4) (D) (1)、(2)、(4)
三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
19.(本题满分12分)本题共有2个小题,第1小题满分4分;第2小题满分4分;第3小题满分4分.
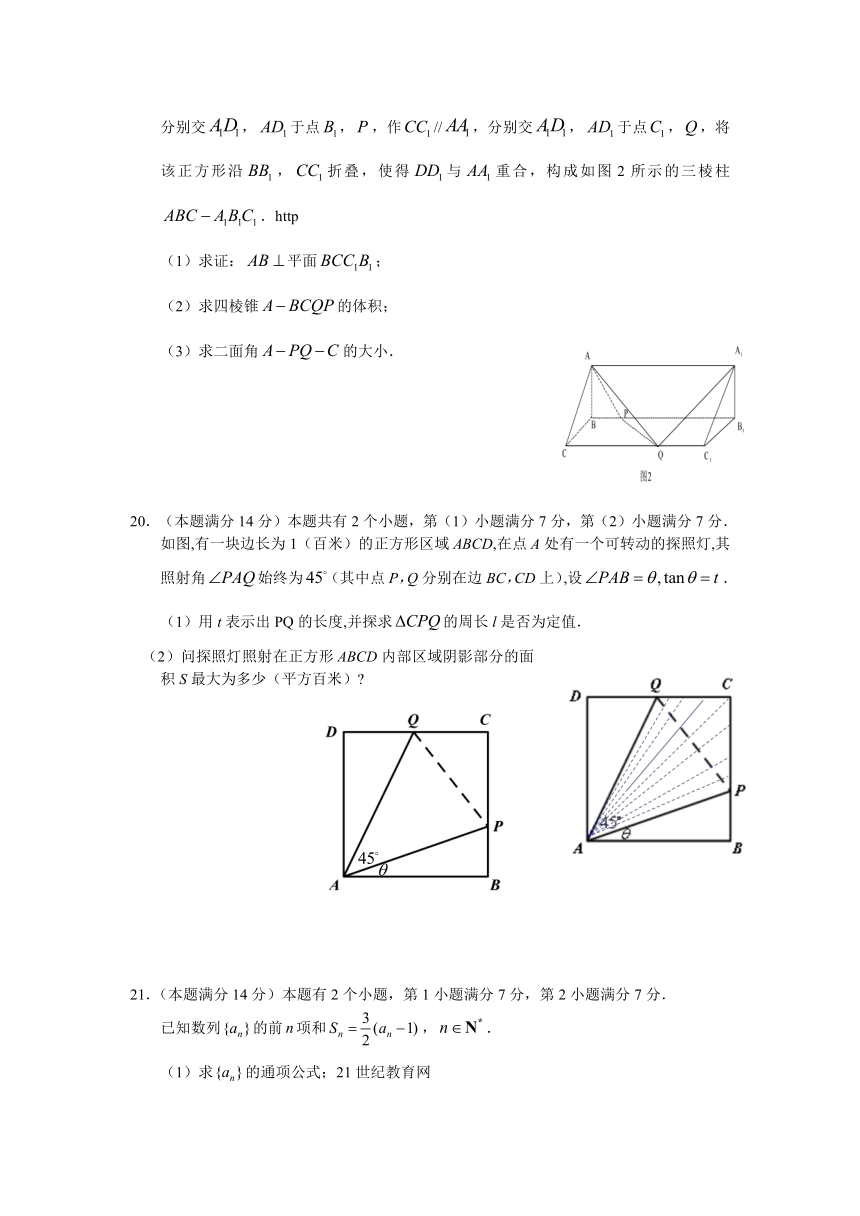
如图所示,在边长为12的正方形中,点在线段上,且,,作//,分别交,于点,,作//,分别交,于点,,将该正方形沿,折叠,使得与重合,构成如图2所示的三棱柱.http
(1)求证:平面;
(2)求四棱锥的体积;
(3)求二面角的大小.
20.(本题满分14分)本题共有2个小题,第(1)小题满分7分,第(2)小题满分7分.
如图,有一块边长为1(百米)的正方形区域ABCD,在点A处有一个可转动的探照灯,其照射角始终为(其中点P,Q分别在边BC,CD上),设.
(1)用t表示出PQ的长度,并探求的周长l是否为定值.
(2)问探照灯照射在正方形ABCD内部区域阴影部分的面积S最大为多少(平方百米)
21.(本题满分14分)本题有2个小题,第1小题满分7分,第2小题满分7分.
已知数列的前项和,.
(1)求的通项公式;21世纪教育网
(2)若对于任意的,有成立,求实数的取值范围.
22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知过点的动直线与圆相交于两点,是中点,与直线相交于.
(1)求证:当与垂直时,必过圆心;
(2)当时,求直线的方程;
(3)探索是否与直线的倾斜角有关 若无关,请求出其值;若有关,请说明理由.
23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知函数,设函数.
(1)求证:函数必有零点
(2)若在上是减函数,求实数的取值范围;
(3)是否存在整数,使得的解集恰好是,若存在,求出的值;若不存在,说明理由.
21世纪教育网
参考答案
一、填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.
1.若函数的反函数为,则 .
2.若复数是纯虚数(i是虚数单位,b为实数),则_________.
3.已知不等式的解集为,则实数的值为_____1_____.
4.已知线性方程组的增广矩阵为,若该线性方程组解为,则实数___.
5.若向量、满足,且与的夹角为,则=___2______.
6.已知圆锥的母线长为,侧面积为,则此圆锥的体积为__________.
7.在中,已知,则 .
8.已知直线的参数方程是,则在轴上的截距为_________.
9.若实数、{,, ,,},且,则方程表示焦点在轴上的双曲线的概率是__________.
10.已知是奇函数, 则的值域为 .
11.数列中,,对于任意,都有,Sn是的前n项和,则___2_____.
12.已知双曲线的两个焦点分别为,该双曲线与抛物线有一个公共的焦点,且两曲线的一个交点为,,则的大小为______.(结果用反三角函数表示)
13.毛毛的计算器中的“开根号”键最近“感冒”了,输出的结果千奇百怪.细心的毛毛在复习资料上发现有一个真命题:已知对于任意正数,则一定在和之间;并且比更接近.毛毛自己编制了一个算法来求的近似值(如图).请你在①中填上适当赋值语句:_______..
14、下图展示了一个区间(0,k)(k是一个给定的正实数)到实数集R的对应过程:区间(0,k)中的实数m对应线段AB上的点M,如图1;将线段AB弯成半圆弧,圆心为H,如图2;再将这个半圆置于直角坐标系中,使得圆心H坐标为(0,1),直径AB平行x轴,如图3;在图形变化过程中,图1中线段AM的长度对应于图3中的圆弧AM的长度,直线HM与直线相交与点N,则与实数m对应的实数就是n,记作.给出下列命题:
(1);(2)函数是奇函数;(3)是定义域上的单调递增函数;
(4)的图象关于点对称;(5)方程的解是.
其中正确命题序号为_(3)(4)(5)______.
二、选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案.考生必须在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.
15.“”是“直线与直线平行”的( B )
(A)充要条件 (B)充分不必要条件
(C)必要不充分条件 (D)既不充分也不必要条件
16.设事件A,B,已知=,=,=,则A,B之间的关系一定为( A ).
(A) 互斥事件; (B) 两个任意事件; (C)非互斥事件; (D)对立事件;
17.若为所在平面内一点,且满足,则ABC的形状为( C )21世纪教育网
(A)正三角形 (B)直角三角形 (C)等腰三角形 (D)等腰直角三角形
18.在平面直角坐标系中,设点,定义,
其中O为坐标原点.对于下列结论:
(1)符合的点P的轨迹围成的图形的面积为2;
(2)设点P是直线:上任意一点,则;
(3)设点P是直线:上任意一点,则“使得最小的点P有无数个”的充要条件是“”;
(4)设点P是椭圆上任意一点,则.
其中正确的结论序号为( A )
(A) (1)、(2) 、(3) (B) (1)、(3) 、(4)
(C) (2)、(3)、(4) (D) (1)、(2)、(4)
三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
19.(本题满分12分)本题共有2个小题,第1小题满分4分,第2小题满分4分.第3小题满分4分.
解.(1)证明:在正方形中,因为,所以三棱柱的底面三角形的边.
因为,,
所以,所以.----------------------------------2分
因为四边形为正方形,,所以,而,
所以平面.--------------------------------------------------------4分
(2)解:因为平面,
所以为四棱锥的高.---------------------------------------5分
因为四边形为直角梯形,且,,
所以梯形的面积为.-----------7分
所以四棱锥的体积.----------8分
(3) 建系如图所示坐标系,则A(0,0,3),P(0,3,0),Q(4,7,0),
-----------------------------------------10分
------------------------------------11分
---------------------------------12分
20.(本题满分14分)本题共有2个小题,第(1)小题满分7分,第(2)小题满分7分.
21世纪教育网
-----------------------------2分
--------------------------------------------------------------4分
---------------------6分
=定值--------------------------------7分
-----------------------10分
--------------------------------------------------12分
------------------------------------------------------13分
-----14分
21.(本题满分14分)本题有2个小题,第1小题满分7分,第2小题满分7分.
已知数列的前项和,.
(1)求的通项公式;
(2)若对于任意的,有成立,求实数的取值范围.
解:(1)因为,,所以.
两式相减,得,即,
∴,.------------------------------------------------4分
又,即,所以.
∴是首项为3,公比为3的等比数列.----------------------------6分
从而的通项公式是,.--------------------------------7分
(2)由(1)知,对于任意的,有成立,
等价于对任意的成立,等价于.-----9分
而,,----------------11分[来源:21世纪教育网]
(注:也可以作差比较证明单调性,相应给分)
∴是单调递减数列.----------------------------------12分
∴,实数的取值范围是.-------------14分
22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.21世纪教育网
已知过点的动直线与圆相交于两点,是中点,与直线相交于.
(1)求证:当与垂直时,必过圆心;
(2)当时,求直线的方程;
(3)探索是否与直线的倾斜角有关 若无关,请求出其值;若有关,请说明理由.
解:(1)与垂直,且
故直线方程为即----------------------2分
圆心坐标(0,3)满足直线方程,
当与垂直时,必过圆心.-----------------------------4分[来源:21世纪教育网]
(2)①当直线与轴垂直时,易知符合题意.----------6分
②当直线与轴不垂直时,设直线的方程为即,
,则由,得,-------8分
直线
故直线的方程为或-----------------------10分
(3)----11分
①当与轴垂直时,易得 则又,
.----------------------------------13分
②当的斜率存在时,设直线的方程为
则由得 则
------------------------15分
综上所述,与直线的斜率无关,且.---------------16分[来源:21世纪教育网]
23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知函数,设函数.
(1)求证:函数必有零点
(2)若在上是减函数,求实数的取值范围;
(3)是否存在整数,使得的解集恰好是,若存在,求出的值;若不存在,说明理由.
解:
-----------------------------------2分
---------4分
[来源:21世纪教育网]
所以----------------------------------------------------------6分
因为在[-1,0]是减函数,所以,解得;所以
当,
因为在[-1,0]是减函数,所以方程的两根均大于零或一根大于零,另一根小于零,且
对称轴--------------------------------------------------------------------------8分
所以 或 解得 所以
综上所述,实数m的取值范围是;-------------------------------------10分21世纪教育网
----------------------------------------------------------12分
---------------------------14分
----------------------------------------------16分
--------------------18分
是
否
输出y
结束
开始
输入x=1
①
y
M
A
B
m
A
M
B
O
H
x
y=-1
N(n,-2)
y=-2
x
y=-2
图1
图2
图3
B
A
H
M
是
否
输出y
结束
开始
输入x=1
①
y
M
A
B
m
A
M
B
O
H
x
y=-1
N(n,-2)
y=-2
x
y=-2
图1
图2
图3
B
A
H
M
x
z
y
2011—2012学年度高三第二学期考试
数 学 试 题(理)
一、填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.
1.若函数的反函数为,则 .
2.若复数是纯虚数(i是虚数单位,b为实数),则_________.
3.已知不等式的解集为,则实数的值为__________.
4.已知线性方程组的增广矩阵为,若该线性方程组解为,则实数___.
5.若向量、满足,且与的夹角为,则=________.
6.已知圆锥的母线长为,侧面积为,则此圆锥的体积为__________.
7.在中,已知,则 .
8.已知直线的参数方程是,则在轴上的截距为________.
9.若实数、{,, ,,},且,则方程表示焦点在轴上的双曲线的概率是__________.
10.已知是奇函数, 则的值域为 .
11.数列中,,对于任意,都有,Sn是的前n项和,则________.
12.已知双曲线的两个焦点分别为,该双曲线与抛物线有一个公共的焦点,且两曲线的一个交点为,,则的大小为______.(结果用反三角函数表示)
13.毛毛的计算器中的“开根号”键最近“感冒”了,输出的结果千奇百怪.细心的毛毛在复习资料上发现有一个真命题:已知对于任意正数,则一定在和之间;并且比更接近.毛毛自己编制了一个算法来求的近似值(如图).请你在①中填上适当赋值语句:_______..
14、下图展示了一个区间(0,k)(k是一个给定的正实数)到实数集R的对应过程:区间(0,k)中的实数m对应线段AB上的点M,如图1;将线段AB弯成半圆弧,圆心为H,如图2;再将这个半圆置于直角坐标系中,使得圆心H坐标为(0,1),直径AB平行x轴,如图3;在图形变化过程中,图1中线段AM的长度对应于图3中的圆弧AM的长度,直线HM与直线相交与点N,则与实数m对应的实数就是n,记作.给出下列命题:
(1);(2)函数是奇函数;(3)是定义域上的单调递增函数;(4)的图象关于点对称;(5)方程的解是.
其中正确命题序号为_______.
二、选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案.考生必须在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.
15.“”是“直线与直线平行”的 ( )
(A)充要条件 (B)充分不必要条件
(C)必要不充分条件 (D)既不充分也不必要条件
16.设事件A,B,已知=,=,=,则A,B之间的关系一定为( ).
(A) 互斥事件; (B)两个任意事件; (C)非互斥事件; (D)对立事件;
17.若为所在平面内一点,且满足,则ABC的形状为 ( )
(A)正三角形 (B)直角三角形 (C)等腰三角形 (D)等腰直角三角形
18.在平面直角坐标系中,设点,定义,其中O为坐标原点.对于下列结论:
(1)符合的点P的轨迹围成的图形的面积为2;
(2)设点P是直线:上任意一点,则;
(3)设点P是直线:上任意一点,则“使得最小的点P有无数个”的充要条件是“”;
(4)设点P是椭圆上任意一点,则.
其中正确的结论序号为 ( )
(A) (1)、(2) 、(3) (B) (1)、(3) 、(4)
(C) (2)、(3)、(4) (D) (1)、(2)、(4)
三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
19.(本题满分12分)本题共有2个小题,第1小题满分4分;第2小题满分4分;第3小题满分4分.
如图所示,在边长为12的正方形中,点在线段上,且,,作//,分别交,于点,,作//,分别交,于点,,将该正方形沿,折叠,使得与重合,构成如图2所示的三棱柱.http
(1)求证:平面;
(2)求四棱锥的体积;
(3)求二面角的大小.
20.(本题满分14分)本题共有2个小题,第(1)小题满分7分,第(2)小题满分7分.
如图,有一块边长为1(百米)的正方形区域ABCD,在点A处有一个可转动的探照灯,其照射角始终为(其中点P,Q分别在边BC,CD上),设.
(1)用t表示出PQ的长度,并探求的周长l是否为定值.
(2)问探照灯照射在正方形ABCD内部区域阴影部分的面积S最大为多少(平方百米)
21.(本题满分14分)本题有2个小题,第1小题满分7分,第2小题满分7分.
已知数列的前项和,.
(1)求的通项公式;21世纪教育网
(2)若对于任意的,有成立,求实数的取值范围.
22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知过点的动直线与圆相交于两点,是中点,与直线相交于.
(1)求证:当与垂直时,必过圆心;
(2)当时,求直线的方程;
(3)探索是否与直线的倾斜角有关 若无关,请求出其值;若有关,请说明理由.
23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知函数,设函数.
(1)求证:函数必有零点
(2)若在上是减函数,求实数的取值范围;
(3)是否存在整数,使得的解集恰好是,若存在,求出的值;若不存在,说明理由.
21世纪教育网
参考答案
一、填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.
1.若函数的反函数为,则 .
2.若复数是纯虚数(i是虚数单位,b为实数),则_________.
3.已知不等式的解集为,则实数的值为_____1_____.
4.已知线性方程组的增广矩阵为,若该线性方程组解为,则实数___.
5.若向量、满足,且与的夹角为,则=___2______.
6.已知圆锥的母线长为,侧面积为,则此圆锥的体积为__________.
7.在中,已知,则 .
8.已知直线的参数方程是,则在轴上的截距为_________.
9.若实数、{,, ,,},且,则方程表示焦点在轴上的双曲线的概率是__________.
10.已知是奇函数, 则的值域为 .
11.数列中,,对于任意,都有,Sn是的前n项和,则___2_____.
12.已知双曲线的两个焦点分别为,该双曲线与抛物线有一个公共的焦点,且两曲线的一个交点为,,则的大小为______.(结果用反三角函数表示)
13.毛毛的计算器中的“开根号”键最近“感冒”了,输出的结果千奇百怪.细心的毛毛在复习资料上发现有一个真命题:已知对于任意正数,则一定在和之间;并且比更接近.毛毛自己编制了一个算法来求的近似值(如图).请你在①中填上适当赋值语句:_______..
14、下图展示了一个区间(0,k)(k是一个给定的正实数)到实数集R的对应过程:区间(0,k)中的实数m对应线段AB上的点M,如图1;将线段AB弯成半圆弧,圆心为H,如图2;再将这个半圆置于直角坐标系中,使得圆心H坐标为(0,1),直径AB平行x轴,如图3;在图形变化过程中,图1中线段AM的长度对应于图3中的圆弧AM的长度,直线HM与直线相交与点N,则与实数m对应的实数就是n,记作.给出下列命题:
(1);(2)函数是奇函数;(3)是定义域上的单调递增函数;
(4)的图象关于点对称;(5)方程的解是.
其中正确命题序号为_(3)(4)(5)______.
二、选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案.考生必须在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.
15.“”是“直线与直线平行”的( B )
(A)充要条件 (B)充分不必要条件
(C)必要不充分条件 (D)既不充分也不必要条件
16.设事件A,B,已知=,=,=,则A,B之间的关系一定为( A ).
(A) 互斥事件; (B) 两个任意事件; (C)非互斥事件; (D)对立事件;
17.若为所在平面内一点,且满足,则ABC的形状为( C )21世纪教育网
(A)正三角形 (B)直角三角形 (C)等腰三角形 (D)等腰直角三角形
18.在平面直角坐标系中,设点,定义,
其中O为坐标原点.对于下列结论:
(1)符合的点P的轨迹围成的图形的面积为2;
(2)设点P是直线:上任意一点,则;
(3)设点P是直线:上任意一点,则“使得最小的点P有无数个”的充要条件是“”;
(4)设点P是椭圆上任意一点,则.
其中正确的结论序号为( A )
(A) (1)、(2) 、(3) (B) (1)、(3) 、(4)
(C) (2)、(3)、(4) (D) (1)、(2)、(4)
三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
19.(本题满分12分)本题共有2个小题,第1小题满分4分,第2小题满分4分.第3小题满分4分.
解.(1)证明:在正方形中,因为,所以三棱柱的底面三角形的边.
因为,,
所以,所以.----------------------------------2分
因为四边形为正方形,,所以,而,
所以平面.--------------------------------------------------------4分
(2)解:因为平面,
所以为四棱锥的高.---------------------------------------5分
因为四边形为直角梯形,且,,
所以梯形的面积为.-----------7分
所以四棱锥的体积.----------8分
(3) 建系如图所示坐标系,则A(0,0,3),P(0,3,0),Q(4,7,0),
-----------------------------------------10分
------------------------------------11分
---------------------------------12分
20.(本题满分14分)本题共有2个小题,第(1)小题满分7分,第(2)小题满分7分.
21世纪教育网
-----------------------------2分
--------------------------------------------------------------4分
---------------------6分
=定值--------------------------------7分
-----------------------10分
--------------------------------------------------12分
------------------------------------------------------13分
-----14分
21.(本题满分14分)本题有2个小题,第1小题满分7分,第2小题满分7分.
已知数列的前项和,.
(1)求的通项公式;
(2)若对于任意的,有成立,求实数的取值范围.
解:(1)因为,,所以.
两式相减,得,即,
∴,.------------------------------------------------4分
又,即,所以.
∴是首项为3,公比为3的等比数列.----------------------------6分
从而的通项公式是,.--------------------------------7分
(2)由(1)知,对于任意的,有成立,
等价于对任意的成立,等价于.-----9分
而,,----------------11分[来源:21世纪教育网]
(注:也可以作差比较证明单调性,相应给分)
∴是单调递减数列.----------------------------------12分
∴,实数的取值范围是.-------------14分
22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.21世纪教育网
已知过点的动直线与圆相交于两点,是中点,与直线相交于.
(1)求证:当与垂直时,必过圆心;
(2)当时,求直线的方程;
(3)探索是否与直线的倾斜角有关 若无关,请求出其值;若有关,请说明理由.
解:(1)与垂直,且
故直线方程为即----------------------2分
圆心坐标(0,3)满足直线方程,
当与垂直时,必过圆心.-----------------------------4分[来源:21世纪教育网]
(2)①当直线与轴垂直时,易知符合题意.----------6分
②当直线与轴不垂直时,设直线的方程为即,
,则由,得,-------8分
直线
故直线的方程为或-----------------------10分
(3)----11分
①当与轴垂直时,易得 则又,
.----------------------------------13分
②当的斜率存在时,设直线的方程为
则由得 则
------------------------15分
综上所述,与直线的斜率无关,且.---------------16分[来源:21世纪教育网]
23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知函数,设函数.
(1)求证:函数必有零点
(2)若在上是减函数,求实数的取值范围;
(3)是否存在整数,使得的解集恰好是,若存在,求出的值;若不存在,说明理由.
解:
-----------------------------------2分
---------4分
[来源:21世纪教育网]
所以----------------------------------------------------------6分
因为在[-1,0]是减函数,所以,解得;所以
当,
因为在[-1,0]是减函数,所以方程的两根均大于零或一根大于零,另一根小于零,且
对称轴--------------------------------------------------------------------------8分
所以 或 解得 所以
综上所述,实数m的取值范围是;-------------------------------------10分21世纪教育网
----------------------------------------------------------12分
---------------------------14分
----------------------------------------------16分
--------------------18分
是
否
输出y
结束
开始
输入x=1
①
y
M
A
B
m
A
M
B
O
H
x
y=-1
N(n,-2)
y=-2
x
y=-2
图1
图2
图3
B
A
H
M
是
否
输出y
结束
开始
输入x=1
①
y
M
A
B
m
A
M
B
O
H
x
y=-1
N(n,-2)
y=-2
x
y=-2
图1
图2
图3
B
A
H
M
x
z
y
同课章节目录
