六年级数学下册试题 一课一练《正比例与反比例》-苏教版(含答案)
文档属性
| 名称 | 六年级数学下册试题 一课一练《正比例与反比例》-苏教版(含答案) | 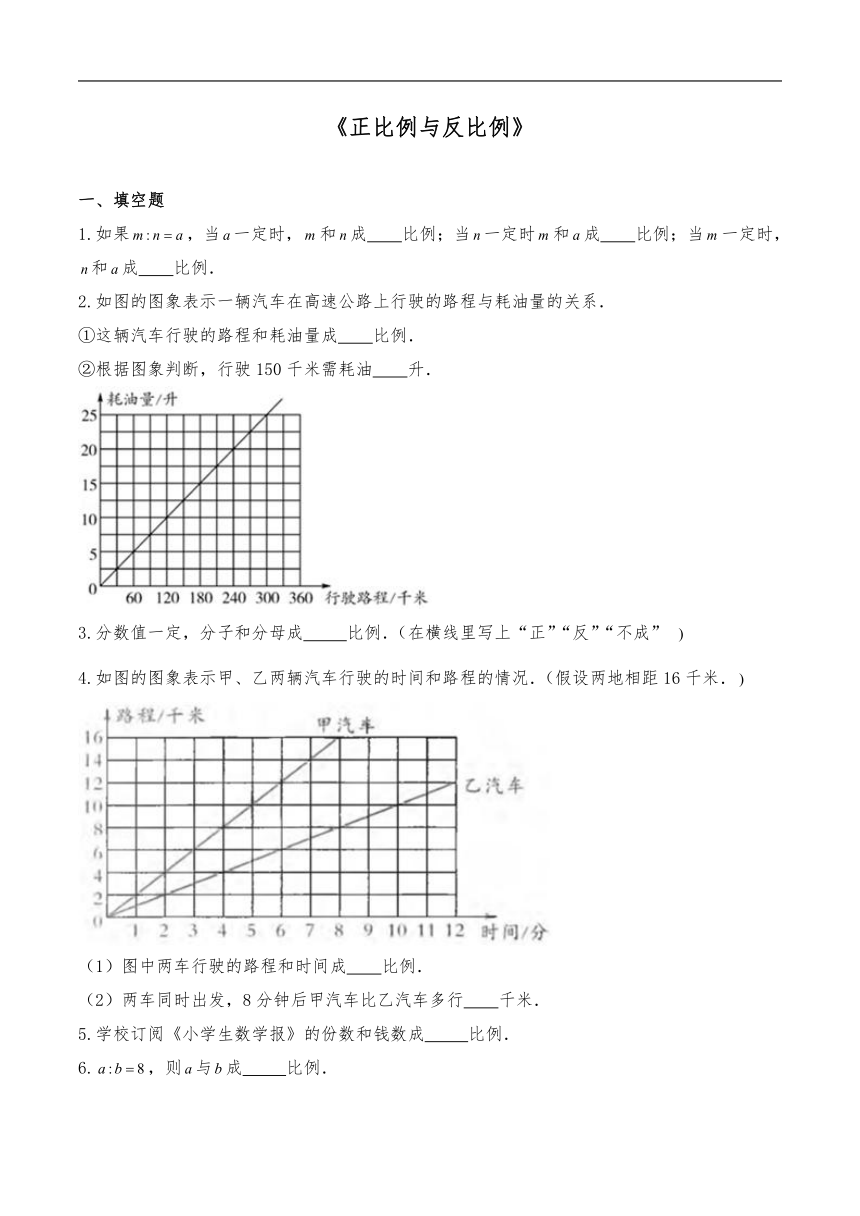 | |
| 格式 | zip | ||
| 文件大小 | 644.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-17 10:16:23 | ||
图片预览





文档简介
《正比例与反比例》
一、填空题
1.如果,当一定时,和成 比例;当一定时和成 比例;当一定时,和成 比例.
2.如图的图象表示一辆汽车在高速公路上行驶的路程与耗油量的关系.
①这辆汽车行驶的路程和耗油量成 比例.
②根据图象判断,行驶150千米需耗油 升.
3.分数值一定,分子和分母成
比例.(在横线里写上“正”“反”“不成”
4.如图的图象表示甲、乙两辆汽车行驶的时间和路程的情况.(假设两地相距16千米.
(1)图中两车行驶的路程和时间成 比例.
(2)两车同时出发,8分钟后甲汽车比乙汽车多行 千米.
5.学校订阅《小学生数学报》的份数和钱数成
比例.
6.,则与成
比例.
7.看表填空.
与 .、成正比例、成反比例
2
3
5
10
4
2.4
12
8.如果,那么与成
比例;已知,则与之间成
比例.
9.判断下面每题中的两种量是不是成比例,如果成比例,成什么比例.
(1)装配一批电视机,每天装配台数和所需的天数 .
(2)正方形的边长和周长 .
(3)水池的容积一定,水管每小时注水量和所用时间 .
(4)房间面积一定,每块砖的面积和铺砖的块数 .
(5)在一定时间里,加工每个零件所用的时间和加工零件的个数 .
(6)在一定时间里,每小时加工零件的个数和加工零件的个数 .
二、选择题
1.下面每题中的两个量,不成正比例的是
A.正方形的周长和边长
B.圆的周长和半径
C.圆的面积和半径
2.长方形的 ,它的长和面积成正比例.
A.周长一定
B.宽一定
C.面积一定
3.圆锥的体积一定,它的底面积和高
A.成正比例
B.成反比例
C.不成比例
D.无法确定
4.固定电话先收座机费24元,以后按一定标准和时间加收通话费,则每月应交电话费与通话时间
A.成正比例
B.成反比例
C.不成比例
5.在同一个圆中,半径与 不成比例.
A.直径
B.周长
C.面积
D.以上都对
6.下面不成比例的是
A.正方形的周长和边长
B.订《中国少年报》的份数和钱数
C.圆柱的体积和底面积
D.某同学从家到学校的步行速度和所用时间
7.
2
3
5
10
4
2.4
12
与
A.成正比例
B.成反比例
三.判断题
1.圆的面积一定,半径和圆周率成反比例.(
)
2.长方形的长一定,面积与宽成正比例,周长与宽成反比例.(
)
3.商品的总价一定,单价和数量成反比例.(
)
4.比值一定,比的前项和后项成正比例.(
)
5.人的年龄和体重成正比例.(
)
6.如果,则与成反比例(
)
7.圆的半径和它的面积不成比例.(
)
8.等边三角形的周长和边长成正比例.(
)
四.应用题
1.右边的图象表示汽车在公路上行驶的路程与耗油量的关系.
①请你用学过的数学知识描述这辆汽车行驶的路程和耗油量的关系,并讲明理由.
②根据图象,这辆汽车行驶耗6升.计算这辆汽车行驶耗油多少升?
2.、两地相距240千米,如果要2小时到达,每小时应行多少千米?如果要3小时、4小时、5小时.到达呢?把表填写完整.
时间时
2
3
4
5
6
速度(千米时)
(1)相对应的两个数的乘积分别是多少?
(2)这个乘积表示什么意义?用数量关系式表示出它与行驶时间和速度之间的关系.
(3)行驶时间和速度成反比例吗?为什么?
五、操作题
1.甲、乙两台机器的工作时间和耗电量如表.
时间时
1
2
3
4
5
6
甲机器耗电量千瓦时
30
60
90
120
150
180
乙机器耗电量千瓦时
30
65
100
130
160
200
根据表中的数据,在下图中描出每一组工作时间与耗电量所对应的点,再把它们按顺序连接起来.
(1)根据画出的图象, 机器的工作时间和耗电量成正比例.
(2)根据画出的图象,工作2.5小时,甲机器的耗电量大约是 千瓦时,乙机器的耗电量大约是 千瓦时.
2.如图是大连到沈阳次高速动车运行情况图.(假设匀速行驶)
(1)从图上看,高速动车4分行驶 千米;
(2)高速动车的速度是 千米时;
(3)高速动车所行驶的路程和时间成 比例;
(4)大连到沈阳的里程是390千米,高速动车需 时到达.
(5)高速动车3.5分大约行驶到哪里,请你在图上标出来.
3.长沙造纸厂的生产情况如下表,根据表回答问题.
时间(天
1
2
3
4
5
6
7
生产量(吨
70
140
210
280
350
420
490
(1)表中相关联的量是
和
.
(2)根据表中的数据,写出一个比例
.
(3)表中相关联的两种量成
关系.
(4)在图中描出表示时间和相应生产量的点,并把它们按顺序连接起来.
(5)估计生产550吨纸片,大约需要
天(填整数).
六、解答题
1.每本演算本售价1.5元,购买2本、3本分别需要多少元?
数量本
0
1
2
3
4
5
6
总价元
0
1.5
3
4.5
6
7.5
9
(1)购买演算本的总价与数量成 比例.
(2)把上表中演算本的数量与总价所对应的点描在方格纸上,再顺次连接.
(3)购买90本演算本需要 元.
(4)奇思购买的演算本的数量是妙想的4倍,他花的钱数是妙想的 倍.
2.下面的图象表示实验小学食堂的用煤天数和用煤量的关系.
(1)根据图象,你能判断用煤天数和用煤量成什么比例吗?
(2)如果用表示用煤的数,表示用煤的天数,表示每天的用煤量,它们之间的关系可以表示为 .
(3)根据图象判断,5天要用煤多少吨?2.4吨煤可用多少天?
3.文具盒每个售价8元,购买2个,3个,分别需要多少元?
(1)填一填.
数量个
0
1
2
3
4
5
6
7
应付金额元
0
8
16
24
32
40
(2)判断应付金额与文具盒的数量是否成正比例,并说明理由.
(3)把上表中数量和应付金额应付金额所对应的点描在方格纸上再顺次连接.
(4)买9个文具盒要花 元.
(5)李老师买的文具盒个数是王老师的5倍,他花的钱是王老师的 倍.
4.把一瓶果汁平均分成若干杯,分的杯数和每杯的果汁量如表.
分的杯数杯
6
5
4
3
每杯的果汁量
100
120
200
(1)请把上表补充完整.
(2)分的杯数和每杯的果汁量有什么关系?为什么?
(3)如果把这些果汁平均分成10杯,每杯的果汁量是多少毫升?
5.看图填空
(1)小明去图书馆每小时行驶 千米,用了 分钟,这段时间内他骑车行驶的路程和时间成 .
(2)他在书店图书馆用去 分钟.
(3)小明从图书馆返回家中的速度是每小时 千米,用了 分钟,这段时间内他骑车行驶的路程和时间成 .
答案
一、填空题
1.正,正,反.
2.正;12.5.
3.正.
4.8.
5.正.
6.正.
7.,6,1,1.2.
8.正,反.
9.成反比例;成正比例;成反比例;成反比例;成正反比例;成正比例.
二、选择题
1..2..3..4..5..6..7..
三.判断题
1..2..3..4..5..6.7..8..
四、应用题
1.解:①汽车行驶路程与耗油量是正比例关系;
因为(一定),
汽车行驶路程与耗油量的比值一定,所以汽车行驶路程与耗油量是正比例关系.
②设这辆汽车行驶耗油升,
.
答:辆汽车行驶耗油14.4升.
2.解:(1)(千米)
答:每小时应行120千米.
(千米)
(千米)
(千米)
(千米)
在这里是路程240千米是一定的,所以相对应的两个数的乘积都是240.
时间时
2
3
4
5
6
速度(千米时)
120
80
60
48
40
(2)相对应的两个数的乘积是速度与时间的乘积,所以这个乘积表示路程,关系式是速度时间路程.
(3)行驶时间和速度成反比例,因为速度时间路程(一定),路程一定,也就是速度与时间的乘积一定,所以速度与时间成反比例.
五、操作题
1.解:先根据统计表中数据,先分别进行描点,再按图示进行依次连线即可;如图:
(1)根据画出的图象,折线在上升过程中各点的连线成一条直线上升的就是机器的工作时间和耗电量成正比例的量,所以甲机器的工作时间和耗电量成正比例,
(2)根据画出的图象估计,工作时间在2小时与3小时中间对应的耗电量,就是甲或乙工作2.5小时各自耗电量;
所以:甲工作2.5小时耗电量:大约75千瓦时,乙工作2.5小时耗电量:大约82.5千瓦时,
故答案为:甲;75,82.5.
2.解:(1)答:高速动车4分钟行驶16千米.
(2)(千米时);
答:高速动车的速度是240千米时.
(3)因为速度(一定),所以高速动车所行驶的路程和时间成正比例.
(4)(小时);
答:高速动车需要1.625小时.
(5)(千米);
故答案为:16;4;正;1.625.
3.解:(1)表中相关联的量是时间(天和生产量(吨.
(2)根据表中的数据,写出一个比例:(答案不唯一).
(3)表中相关联的两种量成正比例关系.
(4)在图中描出表示时间和相应生产量的点,并把它们按顺序连接起来(下图).
(5)估计生产550吨纸片,大约需要8天(填整数)(下图红色虚线与横轴的交点).
故答案为:时间(天,生产量(吨,(答案不唯一),正比例,8.
六、解答题
1.解:(1)购买演算本的总价与数量成正比例.
(2)如图所示:
(3)(元
答:购买90本演算本需要135元.
(4)奇思购买的演算本的数量是妙想的4倍,他花的钱数是妙想的4倍.
故答案为:正;135;4.
2.解:(1)用煤的吨数用煤的天数每天的用煤量(一定)
根据两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就是成正比例的量
因此可判断用煤天数和用煤量成正比例关系.
(2)如果用表示用煤的数,表示用煤的天数,表示每天的用煤量,它们之间的关系可以表示为(一定).
(3)根据图象可判断:5天有煤1.5吨;2.4吨煤可以用8天.
故答案为:(一定).
3.解:(1)(元
(元
表格如下:
数量个
0
1
2
3
4
5
6
7
应付金额元
0
8
16
24
32
40
48
56
(2)因为:(元(元(元
总价数量单价(单价是一定的),所以应付金额与文具盒的数量成正比例.
(3)画图如下:
(4)(元
答:买9个文具盒要花
72元.
(5)根据总价和数量的正比例关系可知:
所以:李老师买的文具盒个数是王老师的5倍,他花的钱是王老师的
5倍.
故答案为:72,5.
4.解:(1)
填表如下:
分的杯数杯
6
5
4
3
每杯的果汁量
100
120
150
200
(2)分的杯数和每杯的果汁量成反比例.因为总量一定,每杯果汁量随着分的杯数的变化而变化;杯数增加,每杯果汁量反而减少;
杯数减少,每杯果汁量反而增加,而
杯数与每杯果汁量的乘积一定.
(3)
答:如果把这些果汁平均分成10杯,每杯的果汁量是60毫升.
故答案为:150.
5.解:(1)30分钟小时,
(千米时),
因为速度(一定),所以这段时间内他骑车的路程和时间成正比例;
答:小强去书店每小时行8千米,用了30分,这段时间内他骑车的路程和时间成正比例.
(2)(分钟);
答:他在书店用去70分.
(3)120分钟分钟分钟小时,
(千米时),
因为速度(一定),所以这段时间内他骑车的路程和时间成正比例;
答:小明从图书馆返回家中的速度是每小时
12千米,用了
20分钟,这段时间内他骑车行驶的路程和时间成
正比例.
故答案为:8,30,正比例;70;12,20,正比例.
一、填空题
1.如果,当一定时,和成 比例;当一定时和成 比例;当一定时,和成 比例.
2.如图的图象表示一辆汽车在高速公路上行驶的路程与耗油量的关系.
①这辆汽车行驶的路程和耗油量成 比例.
②根据图象判断,行驶150千米需耗油 升.
3.分数值一定,分子和分母成
比例.(在横线里写上“正”“反”“不成”
4.如图的图象表示甲、乙两辆汽车行驶的时间和路程的情况.(假设两地相距16千米.
(1)图中两车行驶的路程和时间成 比例.
(2)两车同时出发,8分钟后甲汽车比乙汽车多行 千米.
5.学校订阅《小学生数学报》的份数和钱数成
比例.
6.,则与成
比例.
7.看表填空.
与 .、成正比例、成反比例
2
3
5
10
4
2.4
12
8.如果,那么与成
比例;已知,则与之间成
比例.
9.判断下面每题中的两种量是不是成比例,如果成比例,成什么比例.
(1)装配一批电视机,每天装配台数和所需的天数 .
(2)正方形的边长和周长 .
(3)水池的容积一定,水管每小时注水量和所用时间 .
(4)房间面积一定,每块砖的面积和铺砖的块数 .
(5)在一定时间里,加工每个零件所用的时间和加工零件的个数 .
(6)在一定时间里,每小时加工零件的个数和加工零件的个数 .
二、选择题
1.下面每题中的两个量,不成正比例的是
A.正方形的周长和边长
B.圆的周长和半径
C.圆的面积和半径
2.长方形的 ,它的长和面积成正比例.
A.周长一定
B.宽一定
C.面积一定
3.圆锥的体积一定,它的底面积和高
A.成正比例
B.成反比例
C.不成比例
D.无法确定
4.固定电话先收座机费24元,以后按一定标准和时间加收通话费,则每月应交电话费与通话时间
A.成正比例
B.成反比例
C.不成比例
5.在同一个圆中,半径与 不成比例.
A.直径
B.周长
C.面积
D.以上都对
6.下面不成比例的是
A.正方形的周长和边长
B.订《中国少年报》的份数和钱数
C.圆柱的体积和底面积
D.某同学从家到学校的步行速度和所用时间
7.
2
3
5
10
4
2.4
12
与
A.成正比例
B.成反比例
三.判断题
1.圆的面积一定,半径和圆周率成反比例.(
)
2.长方形的长一定,面积与宽成正比例,周长与宽成反比例.(
)
3.商品的总价一定,单价和数量成反比例.(
)
4.比值一定,比的前项和后项成正比例.(
)
5.人的年龄和体重成正比例.(
)
6.如果,则与成反比例(
)
7.圆的半径和它的面积不成比例.(
)
8.等边三角形的周长和边长成正比例.(
)
四.应用题
1.右边的图象表示汽车在公路上行驶的路程与耗油量的关系.
①请你用学过的数学知识描述这辆汽车行驶的路程和耗油量的关系,并讲明理由.
②根据图象,这辆汽车行驶耗6升.计算这辆汽车行驶耗油多少升?
2.、两地相距240千米,如果要2小时到达,每小时应行多少千米?如果要3小时、4小时、5小时.到达呢?把表填写完整.
时间时
2
3
4
5
6
速度(千米时)
(1)相对应的两个数的乘积分别是多少?
(2)这个乘积表示什么意义?用数量关系式表示出它与行驶时间和速度之间的关系.
(3)行驶时间和速度成反比例吗?为什么?
五、操作题
1.甲、乙两台机器的工作时间和耗电量如表.
时间时
1
2
3
4
5
6
甲机器耗电量千瓦时
30
60
90
120
150
180
乙机器耗电量千瓦时
30
65
100
130
160
200
根据表中的数据,在下图中描出每一组工作时间与耗电量所对应的点,再把它们按顺序连接起来.
(1)根据画出的图象, 机器的工作时间和耗电量成正比例.
(2)根据画出的图象,工作2.5小时,甲机器的耗电量大约是 千瓦时,乙机器的耗电量大约是 千瓦时.
2.如图是大连到沈阳次高速动车运行情况图.(假设匀速行驶)
(1)从图上看,高速动车4分行驶 千米;
(2)高速动车的速度是 千米时;
(3)高速动车所行驶的路程和时间成 比例;
(4)大连到沈阳的里程是390千米,高速动车需 时到达.
(5)高速动车3.5分大约行驶到哪里,请你在图上标出来.
3.长沙造纸厂的生产情况如下表,根据表回答问题.
时间(天
1
2
3
4
5
6
7
生产量(吨
70
140
210
280
350
420
490
(1)表中相关联的量是
和
.
(2)根据表中的数据,写出一个比例
.
(3)表中相关联的两种量成
关系.
(4)在图中描出表示时间和相应生产量的点,并把它们按顺序连接起来.
(5)估计生产550吨纸片,大约需要
天(填整数).
六、解答题
1.每本演算本售价1.5元,购买2本、3本分别需要多少元?
数量本
0
1
2
3
4
5
6
总价元
0
1.5
3
4.5
6
7.5
9
(1)购买演算本的总价与数量成 比例.
(2)把上表中演算本的数量与总价所对应的点描在方格纸上,再顺次连接.
(3)购买90本演算本需要 元.
(4)奇思购买的演算本的数量是妙想的4倍,他花的钱数是妙想的 倍.
2.下面的图象表示实验小学食堂的用煤天数和用煤量的关系.
(1)根据图象,你能判断用煤天数和用煤量成什么比例吗?
(2)如果用表示用煤的数,表示用煤的天数,表示每天的用煤量,它们之间的关系可以表示为 .
(3)根据图象判断,5天要用煤多少吨?2.4吨煤可用多少天?
3.文具盒每个售价8元,购买2个,3个,分别需要多少元?
(1)填一填.
数量个
0
1
2
3
4
5
6
7
应付金额元
0
8
16
24
32
40
(2)判断应付金额与文具盒的数量是否成正比例,并说明理由.
(3)把上表中数量和应付金额应付金额所对应的点描在方格纸上再顺次连接.
(4)买9个文具盒要花 元.
(5)李老师买的文具盒个数是王老师的5倍,他花的钱是王老师的 倍.
4.把一瓶果汁平均分成若干杯,分的杯数和每杯的果汁量如表.
分的杯数杯
6
5
4
3
每杯的果汁量
100
120
200
(1)请把上表补充完整.
(2)分的杯数和每杯的果汁量有什么关系?为什么?
(3)如果把这些果汁平均分成10杯,每杯的果汁量是多少毫升?
5.看图填空
(1)小明去图书馆每小时行驶 千米,用了 分钟,这段时间内他骑车行驶的路程和时间成 .
(2)他在书店图书馆用去 分钟.
(3)小明从图书馆返回家中的速度是每小时 千米,用了 分钟,这段时间内他骑车行驶的路程和时间成 .
答案
一、填空题
1.正,正,反.
2.正;12.5.
3.正.
4.8.
5.正.
6.正.
7.,6,1,1.2.
8.正,反.
9.成反比例;成正比例;成反比例;成反比例;成正反比例;成正比例.
二、选择题
1..2..3..4..5..6..7..
三.判断题
1..2..3..4..5..6.7..8..
四、应用题
1.解:①汽车行驶路程与耗油量是正比例关系;
因为(一定),
汽车行驶路程与耗油量的比值一定,所以汽车行驶路程与耗油量是正比例关系.
②设这辆汽车行驶耗油升,
.
答:辆汽车行驶耗油14.4升.
2.解:(1)(千米)
答:每小时应行120千米.
(千米)
(千米)
(千米)
(千米)
在这里是路程240千米是一定的,所以相对应的两个数的乘积都是240.
时间时
2
3
4
5
6
速度(千米时)
120
80
60
48
40
(2)相对应的两个数的乘积是速度与时间的乘积,所以这个乘积表示路程,关系式是速度时间路程.
(3)行驶时间和速度成反比例,因为速度时间路程(一定),路程一定,也就是速度与时间的乘积一定,所以速度与时间成反比例.
五、操作题
1.解:先根据统计表中数据,先分别进行描点,再按图示进行依次连线即可;如图:
(1)根据画出的图象,折线在上升过程中各点的连线成一条直线上升的就是机器的工作时间和耗电量成正比例的量,所以甲机器的工作时间和耗电量成正比例,
(2)根据画出的图象估计,工作时间在2小时与3小时中间对应的耗电量,就是甲或乙工作2.5小时各自耗电量;
所以:甲工作2.5小时耗电量:大约75千瓦时,乙工作2.5小时耗电量:大约82.5千瓦时,
故答案为:甲;75,82.5.
2.解:(1)答:高速动车4分钟行驶16千米.
(2)(千米时);
答:高速动车的速度是240千米时.
(3)因为速度(一定),所以高速动车所行驶的路程和时间成正比例.
(4)(小时);
答:高速动车需要1.625小时.
(5)(千米);
故答案为:16;4;正;1.625.
3.解:(1)表中相关联的量是时间(天和生产量(吨.
(2)根据表中的数据,写出一个比例:(答案不唯一).
(3)表中相关联的两种量成正比例关系.
(4)在图中描出表示时间和相应生产量的点,并把它们按顺序连接起来(下图).
(5)估计生产550吨纸片,大约需要8天(填整数)(下图红色虚线与横轴的交点).
故答案为:时间(天,生产量(吨,(答案不唯一),正比例,8.
六、解答题
1.解:(1)购买演算本的总价与数量成正比例.
(2)如图所示:
(3)(元
答:购买90本演算本需要135元.
(4)奇思购买的演算本的数量是妙想的4倍,他花的钱数是妙想的4倍.
故答案为:正;135;4.
2.解:(1)用煤的吨数用煤的天数每天的用煤量(一定)
根据两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就是成正比例的量
因此可判断用煤天数和用煤量成正比例关系.
(2)如果用表示用煤的数,表示用煤的天数,表示每天的用煤量,它们之间的关系可以表示为(一定).
(3)根据图象可判断:5天有煤1.5吨;2.4吨煤可以用8天.
故答案为:(一定).
3.解:(1)(元
(元
表格如下:
数量个
0
1
2
3
4
5
6
7
应付金额元
0
8
16
24
32
40
48
56
(2)因为:(元(元(元
总价数量单价(单价是一定的),所以应付金额与文具盒的数量成正比例.
(3)画图如下:
(4)(元
答:买9个文具盒要花
72元.
(5)根据总价和数量的正比例关系可知:
所以:李老师买的文具盒个数是王老师的5倍,他花的钱是王老师的
5倍.
故答案为:72,5.
4.解:(1)
填表如下:
分的杯数杯
6
5
4
3
每杯的果汁量
100
120
150
200
(2)分的杯数和每杯的果汁量成反比例.因为总量一定,每杯果汁量随着分的杯数的变化而变化;杯数增加,每杯果汁量反而减少;
杯数减少,每杯果汁量反而增加,而
杯数与每杯果汁量的乘积一定.
(3)
答:如果把这些果汁平均分成10杯,每杯的果汁量是60毫升.
故答案为:150.
5.解:(1)30分钟小时,
(千米时),
因为速度(一定),所以这段时间内他骑车的路程和时间成正比例;
答:小强去书店每小时行8千米,用了30分,这段时间内他骑车的路程和时间成正比例.
(2)(分钟);
答:他在书店用去70分.
(3)120分钟分钟分钟小时,
(千米时),
因为速度(一定),所以这段时间内他骑车的路程和时间成正比例;
答:小明从图书馆返回家中的速度是每小时
12千米,用了
20分钟,这段时间内他骑车行驶的路程和时间成
正比例.
故答案为:8,30,正比例;70;12,20,正比例.
