安徽省定远县育才学校2020-2021学年高一下学期5月周测文科数学试题 Word版含答案
文档属性
| 名称 | 安徽省定远县育才学校2020-2021学年高一下学期5月周测文科数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 39.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-17 15:19:38 | ||
图片预览



文档简介
育才学校2020-2021学年度第二学期周测
高一文科试卷
选择题(共12小题,每小题5分,共60分)
1.将函数y=sin(x+)(x∈R)图象上所有点的纵坐标不变,横坐标缩小到原来的,再把图象上各点向左平移个单位长度,所得图象解析式为( )
A.y=sin(2x+π) B.y=sin(x+π)
C.y=sin(2x+π) D.y=sin(x+π)
2.把函数y=sin(2x+)的图象向右平移个单位,再把所得图象上各点的横坐标缩短到原来的,则所得图象的函数解析式是( )
A.y=sin(4x+π) B.y=sin(4x+) C.y=sin 4x D.y=sinx
3.将函数f(x)=2sin(2x+)的图象向右平移φ(φ>0)个单位,再将图象上每一点的横坐标缩短到原来的倍(纵坐标不变),所得图象关于直线x=对称,则φ的最小值为( )
A. B.π C.π D.π
4.对于函数y=sin(2x-),下列说法正确的是( )
A. 函数图象关于点(,0)对称
B. 函数图象关于直线x=对称
C. 将它的图象向左平移个单位,得到y=sin 2x的图象
D. 将图象上各点的横坐标缩小为原来的倍,得到y=sin(x-)的图象
5.设函数f(x)=A的图象关于直线x=对称,它的周期是π,则( )
A.f(x)的图象过点 B.f(x)在上是减函数
C.f(x)的一个对称中心是 D.f(x)的最大值是A
6.函数y=sin(-2x)的单调递增区间是( )
A. [kπ-,kπ+)() B. [kπ-,kπ+]()
C. [kπ-,kπ-)() D.()
7.函数y=sin(ωx+φ)(x∈R,ω>0,0≤φ<2π)的部分图象如下图,则( )
39465259525
A.ω=,φ=
B.ω=,φ=
C.ω=,φ=
D.ω=,φ=
4241800315595
8.函数y=2sin(ωx+φ)(ω>0,-<φ<)的部分图象如图所示,则ω、φ的值分别是( )
A. 2,- B. 2,-
C. 4,- D. 4,
9.若函数f(x)=sin2x-(x∈R),则f(x)是( )
A. 最小正周期为的奇函数 B. 最小正周期为π的奇函数
C. 最小正周期为2π的偶函数 D. 最小正周期为π的偶函数
10.设函数f(x)=2cos2x+sin 2x+a(a为实常数)在区间上的最小值为-4,那么a的值等于( )
A. 4 B. -6 C. -4 D. -3
11.使函数f(x)=sin(2x+θ)+cos(2x+θ)为奇函数的θ的一个值是( )
A. B. C. D.
12.已知函数f(x)=cos 2x+cos(2x-),给出下列结论:
①f(x)是最小正周期为π的偶函数; ②f(x)的图象关于x=对称;
③f(x)的最大值为2;
④将函数y=sin 2x的图象向左平移就得到y=f(x)的图象.
其中正确的是( )
A. ①② B. ②③ C. ②④ D. ③④
二.填空题(共4小题,每小题5分,共20分) 13.化简:sin 40°(tan 10°-)=________.
14.将函数y=sin(-2x)的图象向左平移个单位,所得函数图象的解析式为______________.
15.将函数f(x)=2sin的图象向右平移φ(φ>0)个单位,再将图象上每一点横坐标缩短到原来的倍,所得图象关于直线x=对称,则φ的最小正值为________.
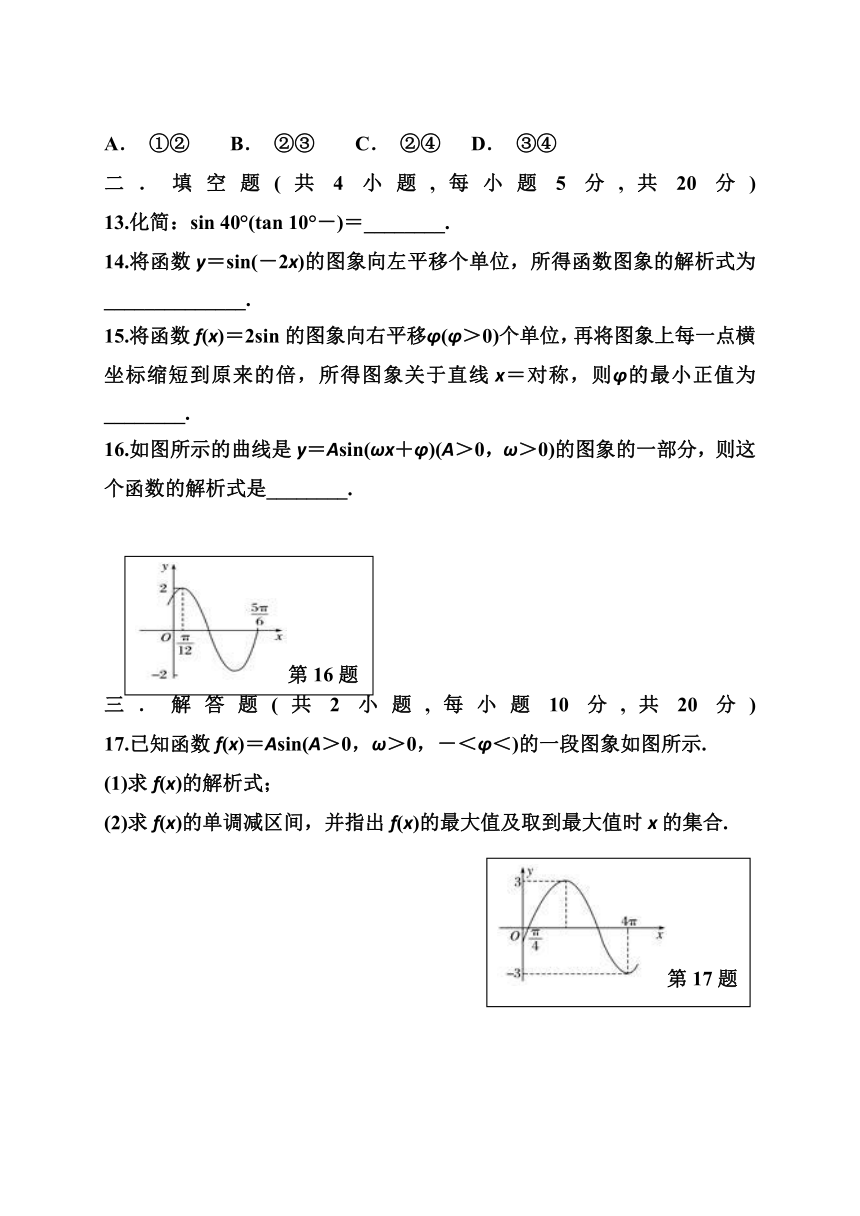
16.如图所示的曲线是y=Asin(ωx+φ)(A>0,ω>0)的图象的一部分,则这个函数的解析式是________.
18415044450第16题
第16题
三.解答题(共2小题,每小题10分,共20分) 17.已知函数f(x)=Asin(A>0,ω>0,-<φ<)的一段图象如图所示.
(1)求f(x)的解析式;
(2)求f(x)的单调减区间,并指出f(x)的最大值及取到最大值时x的集合.
336550088900第17题
第17题
18.已知函数f(x)=sin(π-ωx)cosωx+cos2ωx(ω>0)的最小正周期为π.
(1)求ω的值;
(2)将函数y=f(x)的图象上各点的横坐标缩短到原来的,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在区间上的最小值.
答案解析
1.【答案】C
【解析】将函数y=sin(x+)(x∈R)的图象上所有点的纵坐标不变,横坐标缩小到原来的,可得y=sin(2x+)的图象,再把图象上各点向左平移个单位长度,
则所得的图象的解析式为y=sin[2(x+)+]=sin(2x++)=sin(2x+).
2.【答案】C
【解析】把函数y=sin(2x+)的图象向右平移个单位,可得函数y=sin[2(x-)+]=sin 2x的图象,再把所得图象上各点的横坐标缩短到原来的,可得函数y=sin 4x的图象.
3.【答案】C
【解析】将函数f(x)=2sin(2x+)的图象向右平移φ(φ>0)个单位,
可得y=2sin[2(x-φ)+]=2sin(2x+-2φ)的图象.
再将图象上每一点的横坐标缩短到原来的倍(纵坐标不变),
所得图象对应的函数为y=2sin(4x+-2φ).
再根据所得图象关于直线x=对称,可得4×+-2φ=kπ+,k∈Z,
即φ=-+,故φ的最小值为.
4.【答案】B
【解析】A,将x=代入可得y=sin(2×-)=1,故不正确;
B,将x=代入可得y=sin(2×-)=-1,由正弦函数的图象和性质可知正确;
C,将它的图象向左平移个单位,得到y=sin[2(x+)-]=sin(2x+)的图象,故不正确;
D,将它的图象上各点的横坐标缩小为原来的倍,得到函数y=sin(4x-)的图象,故不正确,故选B.
5.【答案】C
【解析】∵周期T=π,∴=π,∴ω=2.
又∵f(x)的图象关于直线x=对称,
∴2×+φ=kπ+,φ=kπ-.
又|φ|<,∴φ=.∴f(x)=Asin().
∴图象过.
当x=,2x+=π,即f=0时,是f(x)的一个对称中心.
6.【答案】D
【解析】令2kπ+π<2x-≤2kπ+(),2kπ+<2x≤2kπ+(),kπ+<x≤kπ+(),故函数的单调递增区间是(kπ-,kπ-] ().
7.【答案】C
【解析】由所给图象可知,=2,∴T=8.又∵T=,∴ω=.
∵图象在x=1处取得最高点,
∴+φ=+2kπ(k∈Z),
∴φ=2kπ+(k∈Z),∵0≤φ<2π,∴φ=.
8.【答案】A
【解析】(1)由T=+=,得T=π,
∴=π,即ω=2.
又图象过点,则2sin(2×+φ)=2,
∴2×+φ=+2kπ,k∈Z,
∴φ=-+2kπ,k∈Z,
∵-<φ<,
∴φ=-,故选A.
9.【答案】D
【解析】∵y=sin2x-=-=-cos 2x,∴函数f(x)是最小正周期为π的偶函数.
10.【答案】C
【解析】f(x)=2cos2x+sin 2x+a=1+cos 2x+sin 2x+a=2sin+a+1.
当x∈时,2x+∈,∴f(x)min=2·+a+1=-4,∴a=-4.
11.【答案】D
【解析】f(x)=sin(2x+θ)+cos(2x+θ)=2sin.
当θ=时,f(x)=2sin(2x+π)=-2sin 2x为奇函数.
12.【答案】C
【解析】函数f(x)=cos 2x+cos(2x-)=cos 2x+cos 2x+sin 2x=cos 2x+sin 2x=(cos 2x+sin 2x)=sin(2x+),∵f(x)为非奇非偶函数,故①错误;将x=代入t=2x+,得t=.而x=为正弦函数的对称轴,故②正确;显然f(x)的最大值为,③错误;将函数y=sin 2x的图象向左平移就得到y=sin 2(x+)=sin(2x+)=f(x),故④正确.
13.【答案】-1
【解析】原式=sin 40°(-)=(sin 10°-cos 10°)=(sin 10°-cos 10°)
=cos 40°==-1.
14.【答案】y=-cos 2x
【解析】y=sin(-2x)y=sin,
即y=sin=-sin=-cos 2x.
15.【答案】
【解析】由题意得,函数f(x)=2sin变为g(x)=2sin=2sin因为所得图象关于直线x=对称,所以4×-2φ+=+kπ,φ=-(),φ的最小正值为.
16.【答案】y=2sin
【解析】由函数图象可知A=2,T==π,即=π,∴ω=2.
又是五点法作图的第五个点,即2×+φ=2π,∴φ=.
∴所求函数的解析式为y=2sin.
17.【答案】(1)由图象可以得到函数f(x)的振幅A=3,
设函数周期为T,则T=4π-=,所以T=5π,则ω=,
由ωx0+φ=0,得×+φ=0,所以φ=-,
所以f(x)=3sin(x-).
(2)由+2kπ≤x-≤+2kπ(),得+5kπ≤x≤4π+5kπ(),
所以函数的减区间为(+5kπ,4π+5kπ),.
函数f(x)的最大值为3,当且仅当x-=+2kπ,,即x=+5kπ()时函数取得最大值.
所以函数的最大值为3,取得最大值时的x的集合为{x|x=+5kπ()}.
18.【答案】(1)因为f(x)=sin(π-ωx)cosωx+cos2ωx=sinωxcosωx+
=sin 2ωx+cos 2ωx+=sin+,
又ω>0,依题意得=π,所以ω=1.
(2)由(1)知,f(x)=sin+,
所以g(x)=f(2x)=sin+.
当0≤x≤时,≤4x+≤, 所以≤sin≤1.
因此1≤g(x)≤.
故g(x)在区间上的最小值为1.
高一文科试卷
选择题(共12小题,每小题5分,共60分)
1.将函数y=sin(x+)(x∈R)图象上所有点的纵坐标不变,横坐标缩小到原来的,再把图象上各点向左平移个单位长度,所得图象解析式为( )
A.y=sin(2x+π) B.y=sin(x+π)
C.y=sin(2x+π) D.y=sin(x+π)
2.把函数y=sin(2x+)的图象向右平移个单位,再把所得图象上各点的横坐标缩短到原来的,则所得图象的函数解析式是( )
A.y=sin(4x+π) B.y=sin(4x+) C.y=sin 4x D.y=sinx
3.将函数f(x)=2sin(2x+)的图象向右平移φ(φ>0)个单位,再将图象上每一点的横坐标缩短到原来的倍(纵坐标不变),所得图象关于直线x=对称,则φ的最小值为( )
A. B.π C.π D.π
4.对于函数y=sin(2x-),下列说法正确的是( )
A. 函数图象关于点(,0)对称
B. 函数图象关于直线x=对称
C. 将它的图象向左平移个单位,得到y=sin 2x的图象
D. 将图象上各点的横坐标缩小为原来的倍,得到y=sin(x-)的图象
5.设函数f(x)=A的图象关于直线x=对称,它的周期是π,则( )
A.f(x)的图象过点 B.f(x)在上是减函数
C.f(x)的一个对称中心是 D.f(x)的最大值是A
6.函数y=sin(-2x)的单调递增区间是( )
A. [kπ-,kπ+)() B. [kπ-,kπ+]()
C. [kπ-,kπ-)() D.()
7.函数y=sin(ωx+φ)(x∈R,ω>0,0≤φ<2π)的部分图象如下图,则( )
39465259525
A.ω=,φ=
B.ω=,φ=
C.ω=,φ=
D.ω=,φ=
4241800315595
8.函数y=2sin(ωx+φ)(ω>0,-<φ<)的部分图象如图所示,则ω、φ的值分别是( )
A. 2,- B. 2,-
C. 4,- D. 4,
9.若函数f(x)=sin2x-(x∈R),则f(x)是( )
A. 最小正周期为的奇函数 B. 最小正周期为π的奇函数
C. 最小正周期为2π的偶函数 D. 最小正周期为π的偶函数
10.设函数f(x)=2cos2x+sin 2x+a(a为实常数)在区间上的最小值为-4,那么a的值等于( )
A. 4 B. -6 C. -4 D. -3
11.使函数f(x)=sin(2x+θ)+cos(2x+θ)为奇函数的θ的一个值是( )
A. B. C. D.
12.已知函数f(x)=cos 2x+cos(2x-),给出下列结论:
①f(x)是最小正周期为π的偶函数; ②f(x)的图象关于x=对称;
③f(x)的最大值为2;
④将函数y=sin 2x的图象向左平移就得到y=f(x)的图象.
其中正确的是( )
A. ①② B. ②③ C. ②④ D. ③④
二.填空题(共4小题,每小题5分,共20分) 13.化简:sin 40°(tan 10°-)=________.
14.将函数y=sin(-2x)的图象向左平移个单位,所得函数图象的解析式为______________.
15.将函数f(x)=2sin的图象向右平移φ(φ>0)个单位,再将图象上每一点横坐标缩短到原来的倍,所得图象关于直线x=对称,则φ的最小正值为________.
16.如图所示的曲线是y=Asin(ωx+φ)(A>0,ω>0)的图象的一部分,则这个函数的解析式是________.
18415044450第16题
第16题
三.解答题(共2小题,每小题10分,共20分) 17.已知函数f(x)=Asin(A>0,ω>0,-<φ<)的一段图象如图所示.
(1)求f(x)的解析式;
(2)求f(x)的单调减区间,并指出f(x)的最大值及取到最大值时x的集合.
336550088900第17题
第17题
18.已知函数f(x)=sin(π-ωx)cosωx+cos2ωx(ω>0)的最小正周期为π.
(1)求ω的值;
(2)将函数y=f(x)的图象上各点的横坐标缩短到原来的,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在区间上的最小值.
答案解析
1.【答案】C
【解析】将函数y=sin(x+)(x∈R)的图象上所有点的纵坐标不变,横坐标缩小到原来的,可得y=sin(2x+)的图象,再把图象上各点向左平移个单位长度,
则所得的图象的解析式为y=sin[2(x+)+]=sin(2x++)=sin(2x+).
2.【答案】C
【解析】把函数y=sin(2x+)的图象向右平移个单位,可得函数y=sin[2(x-)+]=sin 2x的图象,再把所得图象上各点的横坐标缩短到原来的,可得函数y=sin 4x的图象.
3.【答案】C
【解析】将函数f(x)=2sin(2x+)的图象向右平移φ(φ>0)个单位,
可得y=2sin[2(x-φ)+]=2sin(2x+-2φ)的图象.
再将图象上每一点的横坐标缩短到原来的倍(纵坐标不变),
所得图象对应的函数为y=2sin(4x+-2φ).
再根据所得图象关于直线x=对称,可得4×+-2φ=kπ+,k∈Z,
即φ=-+,故φ的最小值为.
4.【答案】B
【解析】A,将x=代入可得y=sin(2×-)=1,故不正确;
B,将x=代入可得y=sin(2×-)=-1,由正弦函数的图象和性质可知正确;
C,将它的图象向左平移个单位,得到y=sin[2(x+)-]=sin(2x+)的图象,故不正确;
D,将它的图象上各点的横坐标缩小为原来的倍,得到函数y=sin(4x-)的图象,故不正确,故选B.
5.【答案】C
【解析】∵周期T=π,∴=π,∴ω=2.
又∵f(x)的图象关于直线x=对称,
∴2×+φ=kπ+,φ=kπ-.
又|φ|<,∴φ=.∴f(x)=Asin().
∴图象过.
当x=,2x+=π,即f=0时,是f(x)的一个对称中心.
6.【答案】D
【解析】令2kπ+π<2x-≤2kπ+(),2kπ+<2x≤2kπ+(),kπ+<x≤kπ+(),故函数的单调递增区间是(kπ-,kπ-] ().
7.【答案】C
【解析】由所给图象可知,=2,∴T=8.又∵T=,∴ω=.
∵图象在x=1处取得最高点,
∴+φ=+2kπ(k∈Z),
∴φ=2kπ+(k∈Z),∵0≤φ<2π,∴φ=.
8.【答案】A
【解析】(1)由T=+=,得T=π,
∴=π,即ω=2.
又图象过点,则2sin(2×+φ)=2,
∴2×+φ=+2kπ,k∈Z,
∴φ=-+2kπ,k∈Z,
∵-<φ<,
∴φ=-,故选A.
9.【答案】D
【解析】∵y=sin2x-=-=-cos 2x,∴函数f(x)是最小正周期为π的偶函数.
10.【答案】C
【解析】f(x)=2cos2x+sin 2x+a=1+cos 2x+sin 2x+a=2sin+a+1.
当x∈时,2x+∈,∴f(x)min=2·+a+1=-4,∴a=-4.
11.【答案】D
【解析】f(x)=sin(2x+θ)+cos(2x+θ)=2sin.
当θ=时,f(x)=2sin(2x+π)=-2sin 2x为奇函数.
12.【答案】C
【解析】函数f(x)=cos 2x+cos(2x-)=cos 2x+cos 2x+sin 2x=cos 2x+sin 2x=(cos 2x+sin 2x)=sin(2x+),∵f(x)为非奇非偶函数,故①错误;将x=代入t=2x+,得t=.而x=为正弦函数的对称轴,故②正确;显然f(x)的最大值为,③错误;将函数y=sin 2x的图象向左平移就得到y=sin 2(x+)=sin(2x+)=f(x),故④正确.
13.【答案】-1
【解析】原式=sin 40°(-)=(sin 10°-cos 10°)=(sin 10°-cos 10°)
=cos 40°==-1.
14.【答案】y=-cos 2x
【解析】y=sin(-2x)y=sin,
即y=sin=-sin=-cos 2x.
15.【答案】
【解析】由题意得,函数f(x)=2sin变为g(x)=2sin=2sin因为所得图象关于直线x=对称,所以4×-2φ+=+kπ,φ=-(),φ的最小正值为.
16.【答案】y=2sin
【解析】由函数图象可知A=2,T==π,即=π,∴ω=2.
又是五点法作图的第五个点,即2×+φ=2π,∴φ=.
∴所求函数的解析式为y=2sin.
17.【答案】(1)由图象可以得到函数f(x)的振幅A=3,
设函数周期为T,则T=4π-=,所以T=5π,则ω=,
由ωx0+φ=0,得×+φ=0,所以φ=-,
所以f(x)=3sin(x-).
(2)由+2kπ≤x-≤+2kπ(),得+5kπ≤x≤4π+5kπ(),
所以函数的减区间为(+5kπ,4π+5kπ),.
函数f(x)的最大值为3,当且仅当x-=+2kπ,,即x=+5kπ()时函数取得最大值.
所以函数的最大值为3,取得最大值时的x的集合为{x|x=+5kπ()}.
18.【答案】(1)因为f(x)=sin(π-ωx)cosωx+cos2ωx=sinωxcosωx+
=sin 2ωx+cos 2ωx+=sin+,
又ω>0,依题意得=π,所以ω=1.
(2)由(1)知,f(x)=sin+,
所以g(x)=f(2x)=sin+.
当0≤x≤时,≤4x+≤, 所以≤sin≤1.
因此1≤g(x)≤.
故g(x)在区间上的最小值为1.
同课章节目录
