人教B版(2019)高中数学必修第二册 第四章指数函数、对数函数与幂函数4.3指数函数与对数函数的关系同步习题(Word含答案解析)
文档属性
| 名称 | 人教B版(2019)高中数学必修第二册 第四章指数函数、对数函数与幂函数4.3指数函数与对数函数的关系同步习题(Word含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 322.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-17 23:25:19 | ||
图片预览




文档简介
4.3 指数函数与对数函数的关系
知识点一 反函数的概念
1.函数y=e2x(x∈R)的反函数为( )
A.y=2ln
x(x>0)
B.y=ln
(2x)(x>0)
C.y=ln
x(x>0)
D.y=ln
(2x)(x>0)
2.已知函数y=log3(3-x)(0≤x<3),则它的反函数是( )
A.y=3-3x(x≥0)
B.y=3+3x(x≤1)
C.y=3+3x(x≥0)
D.y=3-3x(x≤1)
3.函数f(x)=x2+1(x>2)的反函数是( )
A.y=(1≤x<3)
B.y=(x>3)
C.y=-(1≤x<3)
D.y=-(x>3)
4.已知函数y=3x-2a的反函数是y=bx+,则( )
A.a=-6,b=
B.a=1,b=
C.a=6,b=-
D.a=,b=-
5.已知函数f(x)=x2,x∈D的值域是{1,4,9},且函数f(x)存在反函数,这样的f(x)共有________个.
6.若函数f(x)=的反函数是其本身,则实数a=________.
7.已知函数f(x)是以2为周期的偶函数,当0≤x≤1时,f(x)=lg
(x+1),令函数g(x)=f(x)(x∈[1,2]),则g(x)的反函数为________________.
8.已知函数f(x)=x2-2ax+2,x∈[-1,1].
(1)当a=-时,判定此函数有没有反函数,并说明理由;
(2)当a为何值时,此函数存在反函数?并求出此函数的反函数f-1(x).
知识点二 反函数的图像与性质
9.函数y=log2的反函数的定义域为( )
A.(-∞,+∞)
B.(0,+∞)
C.(-∞,0)
D.(-∞,0)∪(0,+∞)
10.已知x>0,f(x)=log3x2的值域是[-1,1],则它的反函数f-1(x)的值域是( )
A.[-1,1]
B.(0,+∞)
C.∪
D.
11.如图,已知函数f(x)=3x-1,则它的反函数y=f-1(x)的大致图像是( )
12.已知函数y=f(x)的反函数为y=f-1(x),则函数y=f(-x)与y=-f-1(x)的图像( )
A.关于y轴对称
B.关于原点对称
C.关于直线x+y=0对称
D.关于直线x-y=0对称
13.给出下列命题:
(1)若奇函数存在反函数,则其反函数也是奇函数;
(2)函数f(x)在区间[a,b]上存在反函数的充要条件是f(x)在区间[a,b]上是单调函数;
(3)函数f(x)在定义域D上的反函数为f-1(x),则对于任意的x0∈D都有f(f-1(x0))=f-1(f(x0))=x0成立.
其中正确的命题为( )
A.(1)
B.(1)(2)
C.(1)(3)
D.(1)(2)(3)
14.已知点(3,9)在函数f(x)=1+ax的图像上,则f(x)的反函数f-1(x)=________.
15.若函数y=f(x)是函数y=g(x)=a2x的反函数(a>0,且a≠1),且f(4)=1,则a=________.
16.若函数y=f(x)的图像过点(0,1),则函数g(x)=f(4-x)的反函数的图像过点________.
17.已知f(x)=,其反函数为f-1(x),若f-1(x)-a=f(x+a)有实数根,则a的取值范围为________.
知识点三 指数函数与对数函数的综合应用
18.设a,b,c均为正数,且2a=,b=,c=log2c,则( )
A.aB.cC.cD.b19.(多选)已知函数f(x)=loga(ax-1)(a>0,a≠1),则下列说法正确的是( )
A.函数f(x)的图像在y轴的一侧
B.函数f(x)为奇函数
C.函数f(x)为定义域上的增函数
D.函数f(x)在定义域内有最大值
20.已知函数f(x)=log2(1-2x).
(1)求函数f(x)的定义域和值域;
(2)求证函数y=f(x)的图像关于直线y=x对称.
易错点一 对反函数的定义理解不清而致误
已知函数y=f(x+1)与函数y=g(x)的图像关于直线y=x对称,且g(x)的图像过定点(1,2020),则y=f-1(x+1)的图像过定点________.
易错点二 不能将问题合理转化致误
设α,β分别是关于x的方程log2x+x-4=0和2x+x-4=0的根,则α+β=________.
一、单项选择题
1.函数y=2x+1(x∈R)的反函数是( )
A.y=1+log2x(x>0)
B.y=log2(x-1)(x>1)
C.y=-1+log2x(x>0)
D.y=log2(x+1)(x>-1)
2.把函数y=logax(a>0且a≠1)的图像绕原点逆时针旋转90°后,新图像的函数解析式是( )
A.y=-ax
B.y=a-x
C.y=loga(-x)
D.y=-logax
3.已知f(x)=-的反函数为f-1(x)=,则f(x)的定义域为( )
A.(-2,0)
B.[-2,2]
C.[-2,0]
D.[0,2]
4.当0A.有且只有一个
B.可能无解
C.可能有3个
D.一定有3个
5.若函数y=ax(a>0,且a≠1)的反函数的图像过点(,a),则a的值为( )
A.2
B.
C.2或
D.3
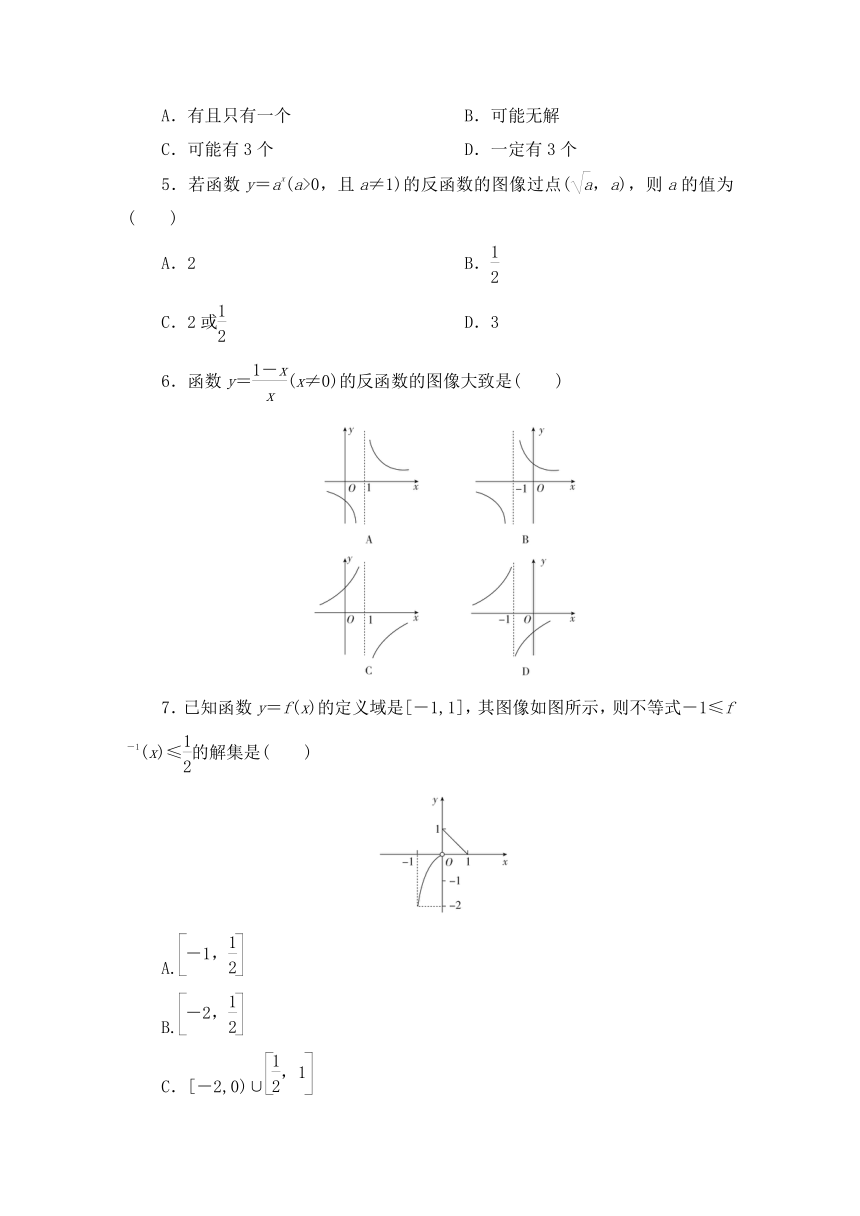
6.函数y=(x≠0)的反函数的图像大致是( )
7.已知函数y=f(x)的定义域是[-1,1],其图像如图所示,则不等式-1≤f-1(x)≤的解集是( )
A.
B.
C.[-2,0)∪
D.[-1,0]∪
8.已知函数f(x)=3x,函数g(x)是f(x)的反函数,若正数x1,x2,…,x2020满足x1x2…x2020=81,则g(x)+g(x)+…+g(x)的值等于( )
A.4
B.8
C.16
D.64
二、多项选择题
9.下列说法中正确的是( )
A.一次函数y=kx+b(k≠0)一定存在反函数
B.若函数f(x)在其定义域内不是单调函数,则f(x)不存在反函数
C.若函数y=f(x)的图像位于第一、二象限,则它的反函数y=f-1(x)的图像位于第一、四象限
D.若函数f(x)存在反函数f-1(x),则f-1(x)与f(x)图像的公共点必在直线y=x上
10.在同一直角坐标系下,函数y=ax与y=logax(a>0,a≠1)的大致图像如图所示,则实数a的可能值为( )
A.
B.
C.
D.
11.如果一个点是一个指数函数的图像与一个对数函数的图像的公共点,那么称这个点为“好点”,在下面的四个点中,是“好点”的有( )
A.(1,2)
B.(2,1)
C.(2,2)
D.(2,0.5)
12.下列说法正确的是( )
A.函数y=ax与y=x图像关于y轴对称
B.函数y=logax与y=图像关于x轴对称
C.函数y=ax与y=logax图像关于直线y=x对称
D.函数y=ax与y=logax图像关于y轴对称
三、填空题
13.函数f(x)=-x2(x∈(-∞,-2])的反函数f-1(x)=________.
14.已知函数f(x)=ax-k的图像过点(1,3),其反函数y=f-1(x)的图像过点(2,0),则f(x)的表达式为________.
15.已知函数f(x)与函数g(x)=的图像关于直线y=x对称,则函数f(x2+2x)的单调增区间是________.
16.已知函数f(x)=loga(a>0,b≠0),则f(x)的值域为____________,f(x)的反函数f-1(x)的解析式为________________.
四、解答题
17.若不等式4x-logax<0,当x∈时恒成立,求实数a的取值范围.
18.已知f(x)=,求f-1的值.
19.已知y=f(x)是R上的增函数,点A(-1,1),B(1,3)在它的图像上,y=f-1(x)是它的反函数,解不等式|f-1(log2x)|<1.
20.已知f(x)=(a∈R),f(0)=0.
(1)求a的值,并判断f(x)的奇偶性;
(2)求f(x)的反函数;
(3)对任意的k∈(0,+∞),解不等式f-1(x)>log2.
4.3 指数函数与对数函数的关系
知识点一 反函数的概念
1.函数y=e2x(x∈R)的反函数为( )
A.y=2ln
x(x>0)
B.y=ln
(2x)(x>0)
C.y=ln
x(x>0)
D.y=ln
(2x)(x>0)
答案 C
解析 y=e2x>0,2x=ln
y,x=ln
y,∴y=e2x的反函数为y=ln
x,x>0.
2.已知函数y=log3(3-x)(0≤x<3),则它的反函数是( )
A.y=3-3x(x≥0)
B.y=3+3x(x≤1)
C.y=3+3x(x≥0)
D.y=3-3x(x≤1)
答案 D
解析 ∵0≤x<3,∴y≤1.又3-x=3y,∴x=3-3y.
∴y=log3(3-x)的反函数为y=3-3x,x≤1.
3.函数f(x)=x2+1(x>2)的反函数是( )
A.y=(1≤x<3)
B.y=(x>3)
C.y=-(1≤x<3)
D.y=-(x>3)
答案 B
解析 令y=x2+1.∵x>2,∴y=x2+1>3.对调函数中的x和y得x=y2+1,解得y=.∴所求反函数为y=(x>3).
4.已知函数y=3x-2a的反函数是y=bx+,则( )
A.a=-6,b=
B.a=1,b=
C.a=6,b=-
D.a=,b=-
答案 B
解析 ∵函数y=3x-2a,∴x=,互换x,y,得函数y=3x-2a的反函数是y=x+a,x∈R.∵函数y=3x-2a的反函数是y=bx+,∴解得a=1,b=.故选B.
5.已知函数f(x)=x2,x∈D的值域是{1,4,9},且函数f(x)存在反函数,这样的f(x)共有________个.
答案 8
解析 当x2=1时,x=±1;当x2=4时,x=±2;当x2=9时,x=±3.若函数f(x)存在反函数,则一个y只能对应一个x,列举如下:
故这样的f(x)共有8个.
6.若函数f(x)=的反函数是其本身,则实数a=________.
答案 -2
解析 函数y=f(x)=的反函数为x=,即y=,因为函数f(x)=的反函数是其本身,所以=,所以a=-2.
7.已知函数f(x)是以2为周期的偶函数,当0≤x≤1时,f(x)=lg
(x+1),令函数g(x)=f(x)(x∈[1,2]),则g(x)的反函数为________________.
答案 g-1(x)=3-10x(0≤x≤lg
2)
解析 当-1≤x≤0时,0≤-x≤1,∴f(x)=f(-x)=lg
(-x+1);当1≤x≤2时,-1≤x-2≤0,∴f(x)=f(x-2)=lg
[-(x-2)+1]=lg
(-x+3).∴g(x)=lg
(-x+3)(1≤x≤2),∴-x+3=10g(x),∴x=3-10g(x).故反函数为g-1(x)=3-10x(0≤x≤lg
2).
8.已知函数f(x)=x2-2ax+2,x∈[-1,1].
(1)当a=-时,判定此函数有没有反函数,并说明理由;
(2)当a为何值时,此函数存在反函数?并求出此函数的反函数f-1(x).
解 (1)当a=-时,f(x)=x2+x+2=2+,x∈[-1,1],显然函数不单调,所以此时没有反函数.
(2)函数存在反函数时必须在[-1,1]上单调,而f(x)=(x-a)2+2-a2,x∈[-1,1],对称轴x=a,所以a≥1或a≤-1.当a≥1时,f-1(x)=a-,x∈[3-2a,3+2a];当a≤-1时,f-1(x)=a+,x∈[3+2a,3-2a].
知识点二 反函数的图像与性质
9.函数y=log2的反函数的定义域为( )
A.(-∞,+∞)
B.(0,+∞)
C.(-∞,0)
D.(-∞,0)∪(0,+∞)
答案 A
解析 反函数的定义域即为原函数的值域.由>0可得log2∈R,所以原函数的值域为R,故它的反函数的定义域为R.故选A.
10.已知x>0,f(x)=log3x2的值域是[-1,1],则它的反函数f-1(x)的值域是( )
A.[-1,1]
B.(0,+∞)
C.∪
D.
答案 D
解析 ∵f(x)=log3x2的值域是[-1,1],∴-1≤log3x2≤1,即≤x2≤3,而x>0,∴x∈.∵反函数的值域为原函数的定义域,∴反函数f-1(x)的值域是.
11.如图,已知函数f(x)=3x-1,则它的反函数y=f-1(x)的大致图像是( )
答案 C
解析 由f(x)=3x-1可得f-1(x)=log3x+1,∴图像为C.
12.已知函数y=f(x)的反函数为y=f-1(x),则函数y=f(-x)与y=-f-1(x)的图像( )
A.关于y轴对称
B.关于原点对称
C.关于直线x+y=0对称
D.关于直线x-y=0对称
答案 D
解析 函数y=f(-x)与y=-f-1(x)互为反函数,图像关于直线x-y=0对称.故选D.
13.给出下列命题:
(1)若奇函数存在反函数,则其反函数也是奇函数;
(2)函数f(x)在区间[a,b]上存在反函数的充要条件是f(x)在区间[a,b]上是单调函数;
(3)函数f(x)在定义域D上的反函数为f-1(x),则对于任意的x0∈D都有f(f-1(x0))=f-1(f(x0))=x0成立.
其中正确的命题为( )
A.(1)
B.(1)(2)
C.(1)(3)
D.(1)(2)(3)
答案 A
解析 (1)设奇函数f(x)的反函数为f-1(x),∵f(x)是奇函数,∴f(x)的值域关于原点对称,即f-1(x)的定义域关于原点对称.假设f(x)=y,则f(-x)=-y.∴f-1(y)=x,f-1(-y)=-x.∴f-1(-y)=-f-1(y),即f-1(-x)=-f-1(x).∴f-1(x)是奇函数.故(1)正确;
(2)函数f(x)在区间[a,b]上存在反函数,不一定f(x)在区间[a,b]上是单调函数,
比如f(x)=存在反函数,但f(x)在R上不单调,故(2)不正确;
(3)x0不一定属于f(x)的值域,即f-1(x0)不一定存在,故(3)不正确.故选A.
14.已知点(3,9)在函数f(x)=1+ax的图像上,则f(x)的反函数f-1(x)=________.
答案 log2(x-1)(x>1)
解析 ∵(3,9)在函数f(x)上,∴1+a3=9,解得a=2,∴f(x)=1+2x,又f(x)>1,∴f-1(x)=log2(x-1)(x>1).
15.若函数y=f(x)是函数y=g(x)=a2x的反函数(a>0,且a≠1),且f(4)=1,则a=________.
答案 2
解析 由y=f(x)与y=g(x)互为反函数,且f(4)=1,得g(1)=4,所以a2=4,a=2.
16.若函数y=f(x)的图像过点(0,1),则函数g(x)=f(4-x)的反函数的图像过点________.
答案 (1,4)
解析 ∵y=f(x)的图像过点(0,1),∴f(4-x)的图像过点(4,1),∴g(x)=f(4-x)的反函数的图像过点(1,4).
17.已知f(x)=,其反函数为f-1(x),若f-1(x)-a=f(x+a)有实数根,则a的取值范围为________.
答案
解析 因为y=f-1(x)-a与y=f(x+a)互为反函数,所以二者关于y=x对称.若y=f-1(x)-a与y=f(x+a)有实数根,则y=f(x+a)与y=x有交点,所以=x,即a=x2-x+1=2+≥.
知识点三 指数函数与对数函数的综合应用
18.设a,b,c均为正数,且2a=,b=,c=log2c,则( )
A.aB.cC.cD.b答案 A
解析 在同一平面直角坐标系中,画出函数y=2x,y=x,y=log2x,y=的图像,如图所示,则a,b,c分别为两个图像交点的横坐标,根据图像可知a19.(多选)已知函数f(x)=loga(ax-1)(a>0,a≠1),则下列说法正确的是( )
A.函数f(x)的图像在y轴的一侧
B.函数f(x)为奇函数
C.函数f(x)为定义域上的增函数
D.函数f(x)在定义域内有最大值
答案 AC
解析 ∵函数f(x)=loga(ax-1)(a>0,a≠1),当a>1时,由ax-1>0,可得x>0,此时,函数的图像仅在y轴的右侧;当00,可得x<0,此时,函数的图像仅在y轴的左侧,故A正确.由于f(-x)=loga(a-x-1)=loga≠-f(x),故函数不是奇函数,故B不正确.由于函数y=logat和函数t=ax的单调性相同,即同是增函数或同是减函数,根据复合函数的单调性可得f(x)=loga(ax-1)在它的定义域内一定是增函数,故C正确.由于t=ax-1无最值,故y=logat无最值,故D不正确.故选AC.
20.已知函数f(x)=log2(1-2x).
(1)求函数f(x)的定义域和值域;
(2)求证函数y=f(x)的图像关于直线y=x对称.
解 (1)要使函数f(x)=log2(1-2x)有意义,
则1-2x>0,即2x<1.
故x<0,此时0<1-2x<1,
∴f(x)=log2(1-2x)<0,
故函数f(x)的定义域为(-∞,0),值域为(-∞,0).
(2)证明:由y=f(x)=log2(1-2x)可得1-2x=2y,解得x=log2(1-2y),故原函数的反函数为f-1(x)=log2(1-2x),与原函数相同,所以函数f(x)的图像关于直线y=x对称.
易错点一 对反函数的定义理解不清而致误
已知函数y=f(x+1)与函数y=g(x)的图像关于直线y=x对称,且g(x)的图像过定点(1,2020),则y=f-1(x+1)的图像过定点________.
易错分析 本题容易误认为f(x+1)与f-1(x+1)互为反函数.
答案 (0,2021)
正解 ∵g(x)的图像过定点(1,2020),
∴f(x+1)的图像过定点(2020,1).
又f(x)的图像可以看作由f(x+1)的图像向右平移一个单位长度得到的,∴f(x)过定点(2021,1).
又f(x)与f-1(x)互为反函数,
∴f-1(x)的图像过定点(1,2021).
再结合f-1(x)与f-1(x+1)的关系可知,
f-1(x+1)的图像过定点(0,2021).
易错点二 不能将问题合理转化致误
设α,β分别是关于x的方程log2x+x-4=0和2x+x-4=0的根,则α+β=________.
易错分析 本题的易错之处为不能正确将问题转化为函数y=log2x,y=2x,y=4-x三个图像之间的关系进行求解.
答案 4
正解 如图,分别作出函数y=log2x,y=2x,y=4-x的图像,相交于点P,Q.∵log2α=4-α,2β=4-β.而y=log2x(x>0)与y=2x互为反函数,直线y=4-x与直线y=x互相垂直,∴点P与Q关于直线y=x对称.
∴α=2β=4-β.∴α+β=4.
一、单项选择题
1.函数y=2x+1(x∈R)的反函数是( )
A.y=1+log2x(x>0)
B.y=log2(x-1)(x>1)
C.y=-1+log2x(x>0)
D.y=log2(x+1)(x>-1)
答案 C
解析 由y=2x+1?x+1=log2y?x=-1+log2y,又因原函数的值域{y|y>0},故其反函数是y=-1+log2x(x>0).
2.把函数y=logax(a>0且a≠1)的图像绕原点逆时针旋转90°后,新图像的函数解析式是( )
A.y=-ax
B.y=a-x
C.y=loga(-x)
D.y=-logax
答案 B
解析 函数的图像绕坐标原点逆时针旋转90°后,得到的函数与原函数的反函数的图像关于y轴对称.函数y=logax(a>0且a≠1)的反函数为y=ax,其关于y轴对称的函数解析式为y=a-x.故选B.
3.已知f(x)=-的反函数为f-1(x)=,则f(x)的定义域为( )
A.(-2,0)
B.[-2,2]
C.[-2,0]
D.[0,2]
答案 D
解析 ∵原函数的定义域就是反函数的值域,原函数的值域就是反函数的定义域.∴解得即0≤x≤2.故f(x)的定义域为[0,2].故选D.
4.当0A.有且只有一个
B.可能无解
C.可能有3个
D.一定有3个
答案 C
解析 考虑函数y=logax与函数y=ax的图像公共点,易知B,D两项不对.又y=和y=x的图像除了在直线y=x上存在一个公共点外,还存在和两个公共点.故选C.
5.若函数y=ax(a>0,且a≠1)的反函数的图像过点(,a),则a的值为( )
A.2
B.
C.2或
D.3
答案 B
解析 解法一:函数y=ax(a>0,且a≠1)的反函数即y=logax,故y=logax的图像过点(,a),则a=loga=.
解法二:由题意得,函数y=ax(a>0,且a≠1)的反函数的图像过点(,a),则函数y=ax(a>0,且a≠1)的图像过点(a,),即aa==,故a=.
6.函数y=(x≠0)的反函数的图像大致是( )
答案 B
解析 y=(x≠0)的反函数为y=(x≠-1),其图像为y=的图像向左平移1个单位长度.
7.已知函数y=f(x)的定义域是[-1,1],其图像如图所示,则不等式-1≤f-1(x)≤的解集是( )
A.
B.
C.[-2,0)∪
D.[-1,0]∪
答案 C
解析 由题意,可得-1≤f-1(x)≤的解集即为f(x)在上的值域.当-1≤x<0时,由题图可知f(x)∈[-2,0),当0≤x≤时,由题图可知f(x)∈.故不等式-1≤f-1(x)≤的解集为[-2,0)∪.
8.已知函数f(x)=3x,函数g(x)是f(x)的反函数,若正数x1,x2,…,x2020满足x1x2…x2020=81,则g(x)+g(x)+…+g(x)的值等于( )
A.4
B.8
C.16
D.64
答案 B
解析 由函数f(x)=3x,函数g(x)是f(x)的反函数,则g(x)=log3x,所以g(x)+g(x)+…+g(x)=log3(x1x2…x2020)2=2log3(x1x2…x2020)=2log381=8.故选B.
二、多项选择题
9.下列说法中正确的是( )
A.一次函数y=kx+b(k≠0)一定存在反函数
B.若函数f(x)在其定义域内不是单调函数,则f(x)不存在反函数
C.若函数y=f(x)的图像位于第一、二象限,则它的反函数y=f-1(x)的图像位于第一、四象限
D.若函数f(x)存在反函数f-1(x),则f-1(x)与f(x)图像的公共点必在直线y=x上
答案 AC
解析 对于A,一次函数y=kx+b(k≠0)为单调函数,一定存在反函数,故正确;对于B,因为函数f(x)=在定义域上不单调,但函数f(x)存在反函数,故错误;对于C,因为原函数与它的反函数的图像关于y=x对称,所以将y=f(x)的图像沿y=x翻折后,会落在第一、四象限,故正确;对于D,比如函数y=-与其反函数y=x2-1(x≤0)的交点坐标有(-1,0),(0,-1),显然交点不在直线y=x上,故错误.故选AC.
10.在同一直角坐标系下,函数y=ax与y=logax(a>0,a≠1)的大致图像如图所示,则实数a的可能值为( )
A.
B.
C.
D.
答案 BC
解析 由图像可知a>1且a22=>2,故A错误;2=<2=<2,故B正确;2=<2=<2,故C正确;2=>2=>2,故D错误.综上,选BC.
11.如果一个点是一个指数函数的图像与一个对数函数的图像的公共点,那么称这个点为“好点”,在下面的四个点中,是“好点”的有( )
A.(1,2)
B.(2,1)
C.(2,2)
D.(2,0.5)
答案 CD
解析 当x=1时,对数函数y=logax(a>0,a≠1)恒过(1,0)点,故(1,2)一定不是好点;当y=1时,指数函数y=ax(a>0,a≠1)恒过(0,1)点,故(2,1)也一定不是好点;而(2,2)是函数y=()x与的交点;(2,0.5)是函数y=x与y=log4x的交点;故选CD.
12.下列说法正确的是( )
A.函数y=ax与y=x图像关于y轴对称
B.函数y=logax与y=图像关于x轴对称
C.函数y=ax与y=logax图像关于直线y=x对称
D.函数y=ax与y=logax图像关于y轴对称
答案 ABC
解析 令a=2,分别作出对应的图像,由图像可知,对于A,∵函数y=ax与y=x图像关于y轴对称,故A正确;对于B,∵函数y=logax与y=图像关于x轴对称,故B正确;对于C,D,∵函数y=ax与y=logax图像关于直线y=x对称,故C正确,D不正确.故选ABC.
三、填空题
13.函数f(x)=-x2(x∈(-∞,-2])的反函数f-1(x)=________.
答案 -,x∈(-∞,-4]
解析 由y=-x2,x∈(-∞,-2],得y∈(-∞,-4],
∴x=-,即f-1(x)=-,x∈(-∞,-4].
14.已知函数f(x)=ax-k的图像过点(1,3),其反函数y=f-1(x)的图像过点(2,0),则f(x)的表达式为________.
答案 f(x)=2x+1
解析 ∵y=f-1(x)的图像过点(2,0),
∴f(x)的图像过点(0,2),∴2=a0-k,∴k=-1,
∴f(x)=ax+1.
又f(x)的图像过点(1,3),
∴3=a1+1,∴a=2,∴f(x)=2x+1.
15.已知函数f(x)与函数g(x)=的图像关于直线y=x对称,则函数f(x2+2x)的单调增区间是________.
答案 (-∞,-1]
解析 由题意得f(x)=x,∴f(x2+2x)=,∵f(x)在R上是减函数,∴由同增异减的原则可知,所求函数的单调增区间即为t=x2+2x的单调减区间,即(-∞,-1].
16.已知函数f(x)=loga(a>0,b≠0),则f(x)的值域为____________,f(x)的反函数f-1(x)的解析式为________________.
答案 (-∞,0)∪(0,+∞) f-1(x)=b·
解析 ∵b≠0,∴≠1,∴f(x)=loga≠0.由y=loga,化为=ay,解得x=b·.把x与y互换可得y=b·,∴f(x)的反函数f-1(x)=b·.
四、解答题
17.若不等式4x-logax<0,当x∈时恒成立,求实数a的取值范围.
解 要使不等式4x<logax在x∈时恒成立,即函数y=logax的图像在内恒在函数y=4x图像的上方,而y=4x的图像过点.
由图可知,loga≥2,显然这里0<a<1,
∴函数y=logax递减.
又loga≥2=logaa2,∴a2≥,
又0∴所求的a的取值范围为.
18.已知f(x)=,求f-1的值.
解 令y=,∴y+y·3x=1-3x,∴3x=,
∴x=log3,∴f-1(x)=log3.
∴f-1=log3=log3=-2.
19.已知y=f(x)是R上的增函数,点A(-1,1),B(1,3)在它的图像上,y=f-1(x)是它的反函数,解不等式|f-1(log2x)|<1.
解 ∵y=f(x)是R上的增函数,
∴y=f-1(x)在R上也是增函数.
∵f(-1)=1,f(1)=3,∴f-1(1)=-1,f-1(3)=1.
由|f-1(log2x)|<1,得-1∴f-1(1)20.已知f(x)=(a∈R),f(0)=0.
(1)求a的值,并判断f(x)的奇偶性;
(2)求f(x)的反函数;
(3)对任意的k∈(0,+∞),解不等式f-1(x)>log2.
解 (1)由f(0)=0,得a=1,所以f(x)=(x∈R).
因为f(x)+f(-x)=+=+=0,
所以f(-x)=-f(x),即f(x)为奇函数.
(2)因为f(x)=y==1-,
所以2x=(-1<y<1),
所以f-1(x)=log2(-1<x<1).
(3)因为f-1(x)>log2,
即log2>log2,所以
所以
当0<k<2时,原不等式的解集为{x|1-k<x<1};
当k≥2时,原不等式的解集为{x|-1<x<1}.
知识点一 反函数的概念
1.函数y=e2x(x∈R)的反函数为( )
A.y=2ln
x(x>0)
B.y=ln
(2x)(x>0)
C.y=ln
x(x>0)
D.y=ln
(2x)(x>0)
2.已知函数y=log3(3-x)(0≤x<3),则它的反函数是( )
A.y=3-3x(x≥0)
B.y=3+3x(x≤1)
C.y=3+3x(x≥0)
D.y=3-3x(x≤1)
3.函数f(x)=x2+1(x>2)的反函数是( )
A.y=(1≤x<3)
B.y=(x>3)
C.y=-(1≤x<3)
D.y=-(x>3)
4.已知函数y=3x-2a的反函数是y=bx+,则( )
A.a=-6,b=
B.a=1,b=
C.a=6,b=-
D.a=,b=-
5.已知函数f(x)=x2,x∈D的值域是{1,4,9},且函数f(x)存在反函数,这样的f(x)共有________个.
6.若函数f(x)=的反函数是其本身,则实数a=________.
7.已知函数f(x)是以2为周期的偶函数,当0≤x≤1时,f(x)=lg
(x+1),令函数g(x)=f(x)(x∈[1,2]),则g(x)的反函数为________________.
8.已知函数f(x)=x2-2ax+2,x∈[-1,1].
(1)当a=-时,判定此函数有没有反函数,并说明理由;
(2)当a为何值时,此函数存在反函数?并求出此函数的反函数f-1(x).
知识点二 反函数的图像与性质
9.函数y=log2的反函数的定义域为( )
A.(-∞,+∞)
B.(0,+∞)
C.(-∞,0)
D.(-∞,0)∪(0,+∞)
10.已知x>0,f(x)=log3x2的值域是[-1,1],则它的反函数f-1(x)的值域是( )
A.[-1,1]
B.(0,+∞)
C.∪
D.
11.如图,已知函数f(x)=3x-1,则它的反函数y=f-1(x)的大致图像是( )
12.已知函数y=f(x)的反函数为y=f-1(x),则函数y=f(-x)与y=-f-1(x)的图像( )
A.关于y轴对称
B.关于原点对称
C.关于直线x+y=0对称
D.关于直线x-y=0对称
13.给出下列命题:
(1)若奇函数存在反函数,则其反函数也是奇函数;
(2)函数f(x)在区间[a,b]上存在反函数的充要条件是f(x)在区间[a,b]上是单调函数;
(3)函数f(x)在定义域D上的反函数为f-1(x),则对于任意的x0∈D都有f(f-1(x0))=f-1(f(x0))=x0成立.
其中正确的命题为( )
A.(1)
B.(1)(2)
C.(1)(3)
D.(1)(2)(3)
14.已知点(3,9)在函数f(x)=1+ax的图像上,则f(x)的反函数f-1(x)=________.
15.若函数y=f(x)是函数y=g(x)=a2x的反函数(a>0,且a≠1),且f(4)=1,则a=________.
16.若函数y=f(x)的图像过点(0,1),则函数g(x)=f(4-x)的反函数的图像过点________.
17.已知f(x)=,其反函数为f-1(x),若f-1(x)-a=f(x+a)有实数根,则a的取值范围为________.
知识点三 指数函数与对数函数的综合应用
18.设a,b,c均为正数,且2a=,b=,c=log2c,则( )
A.a
A.函数f(x)的图像在y轴的一侧
B.函数f(x)为奇函数
C.函数f(x)为定义域上的增函数
D.函数f(x)在定义域内有最大值
20.已知函数f(x)=log2(1-2x).
(1)求函数f(x)的定义域和值域;
(2)求证函数y=f(x)的图像关于直线y=x对称.
易错点一 对反函数的定义理解不清而致误
已知函数y=f(x+1)与函数y=g(x)的图像关于直线y=x对称,且g(x)的图像过定点(1,2020),则y=f-1(x+1)的图像过定点________.
易错点二 不能将问题合理转化致误
设α,β分别是关于x的方程log2x+x-4=0和2x+x-4=0的根,则α+β=________.
一、单项选择题
1.函数y=2x+1(x∈R)的反函数是( )
A.y=1+log2x(x>0)
B.y=log2(x-1)(x>1)
C.y=-1+log2x(x>0)
D.y=log2(x+1)(x>-1)
2.把函数y=logax(a>0且a≠1)的图像绕原点逆时针旋转90°后,新图像的函数解析式是( )
A.y=-ax
B.y=a-x
C.y=loga(-x)
D.y=-logax
3.已知f(x)=-的反函数为f-1(x)=,则f(x)的定义域为( )
A.(-2,0)
B.[-2,2]
C.[-2,0]
D.[0,2]
4.当0
B.可能无解
C.可能有3个
D.一定有3个
5.若函数y=ax(a>0,且a≠1)的反函数的图像过点(,a),则a的值为( )
A.2
B.
C.2或
D.3
6.函数y=(x≠0)的反函数的图像大致是( )
7.已知函数y=f(x)的定义域是[-1,1],其图像如图所示,则不等式-1≤f-1(x)≤的解集是( )
A.
B.
C.[-2,0)∪
D.[-1,0]∪
8.已知函数f(x)=3x,函数g(x)是f(x)的反函数,若正数x1,x2,…,x2020满足x1x2…x2020=81,则g(x)+g(x)+…+g(x)的值等于( )
A.4
B.8
C.16
D.64
二、多项选择题
9.下列说法中正确的是( )
A.一次函数y=kx+b(k≠0)一定存在反函数
B.若函数f(x)在其定义域内不是单调函数,则f(x)不存在反函数
C.若函数y=f(x)的图像位于第一、二象限,则它的反函数y=f-1(x)的图像位于第一、四象限
D.若函数f(x)存在反函数f-1(x),则f-1(x)与f(x)图像的公共点必在直线y=x上
10.在同一直角坐标系下,函数y=ax与y=logax(a>0,a≠1)的大致图像如图所示,则实数a的可能值为( )
A.
B.
C.
D.
11.如果一个点是一个指数函数的图像与一个对数函数的图像的公共点,那么称这个点为“好点”,在下面的四个点中,是“好点”的有( )
A.(1,2)
B.(2,1)
C.(2,2)
D.(2,0.5)
12.下列说法正确的是( )
A.函数y=ax与y=x图像关于y轴对称
B.函数y=logax与y=图像关于x轴对称
C.函数y=ax与y=logax图像关于直线y=x对称
D.函数y=ax与y=logax图像关于y轴对称
三、填空题
13.函数f(x)=-x2(x∈(-∞,-2])的反函数f-1(x)=________.
14.已知函数f(x)=ax-k的图像过点(1,3),其反函数y=f-1(x)的图像过点(2,0),则f(x)的表达式为________.
15.已知函数f(x)与函数g(x)=的图像关于直线y=x对称,则函数f(x2+2x)的单调增区间是________.
16.已知函数f(x)=loga(a>0,b≠0),则f(x)的值域为____________,f(x)的反函数f-1(x)的解析式为________________.
四、解答题
17.若不等式4x-logax<0,当x∈时恒成立,求实数a的取值范围.
18.已知f(x)=,求f-1的值.
19.已知y=f(x)是R上的增函数,点A(-1,1),B(1,3)在它的图像上,y=f-1(x)是它的反函数,解不等式|f-1(log2x)|<1.
20.已知f(x)=(a∈R),f(0)=0.
(1)求a的值,并判断f(x)的奇偶性;
(2)求f(x)的反函数;
(3)对任意的k∈(0,+∞),解不等式f-1(x)>log2.
4.3 指数函数与对数函数的关系
知识点一 反函数的概念
1.函数y=e2x(x∈R)的反函数为( )
A.y=2ln
x(x>0)
B.y=ln
(2x)(x>0)
C.y=ln
x(x>0)
D.y=ln
(2x)(x>0)
答案 C
解析 y=e2x>0,2x=ln
y,x=ln
y,∴y=e2x的反函数为y=ln
x,x>0.
2.已知函数y=log3(3-x)(0≤x<3),则它的反函数是( )
A.y=3-3x(x≥0)
B.y=3+3x(x≤1)
C.y=3+3x(x≥0)
D.y=3-3x(x≤1)
答案 D
解析 ∵0≤x<3,∴y≤1.又3-x=3y,∴x=3-3y.
∴y=log3(3-x)的反函数为y=3-3x,x≤1.
3.函数f(x)=x2+1(x>2)的反函数是( )
A.y=(1≤x<3)
B.y=(x>3)
C.y=-(1≤x<3)
D.y=-(x>3)
答案 B
解析 令y=x2+1.∵x>2,∴y=x2+1>3.对调函数中的x和y得x=y2+1,解得y=.∴所求反函数为y=(x>3).
4.已知函数y=3x-2a的反函数是y=bx+,则( )
A.a=-6,b=
B.a=1,b=
C.a=6,b=-
D.a=,b=-
答案 B
解析 ∵函数y=3x-2a,∴x=,互换x,y,得函数y=3x-2a的反函数是y=x+a,x∈R.∵函数y=3x-2a的反函数是y=bx+,∴解得a=1,b=.故选B.
5.已知函数f(x)=x2,x∈D的值域是{1,4,9},且函数f(x)存在反函数,这样的f(x)共有________个.
答案 8
解析 当x2=1时,x=±1;当x2=4时,x=±2;当x2=9时,x=±3.若函数f(x)存在反函数,则一个y只能对应一个x,列举如下:
故这样的f(x)共有8个.
6.若函数f(x)=的反函数是其本身,则实数a=________.
答案 -2
解析 函数y=f(x)=的反函数为x=,即y=,因为函数f(x)=的反函数是其本身,所以=,所以a=-2.
7.已知函数f(x)是以2为周期的偶函数,当0≤x≤1时,f(x)=lg
(x+1),令函数g(x)=f(x)(x∈[1,2]),则g(x)的反函数为________________.
答案 g-1(x)=3-10x(0≤x≤lg
2)
解析 当-1≤x≤0时,0≤-x≤1,∴f(x)=f(-x)=lg
(-x+1);当1≤x≤2时,-1≤x-2≤0,∴f(x)=f(x-2)=lg
[-(x-2)+1]=lg
(-x+3).∴g(x)=lg
(-x+3)(1≤x≤2),∴-x+3=10g(x),∴x=3-10g(x).故反函数为g-1(x)=3-10x(0≤x≤lg
2).
8.已知函数f(x)=x2-2ax+2,x∈[-1,1].
(1)当a=-时,判定此函数有没有反函数,并说明理由;
(2)当a为何值时,此函数存在反函数?并求出此函数的反函数f-1(x).
解 (1)当a=-时,f(x)=x2+x+2=2+,x∈[-1,1],显然函数不单调,所以此时没有反函数.
(2)函数存在反函数时必须在[-1,1]上单调,而f(x)=(x-a)2+2-a2,x∈[-1,1],对称轴x=a,所以a≥1或a≤-1.当a≥1时,f-1(x)=a-,x∈[3-2a,3+2a];当a≤-1时,f-1(x)=a+,x∈[3+2a,3-2a].
知识点二 反函数的图像与性质
9.函数y=log2的反函数的定义域为( )
A.(-∞,+∞)
B.(0,+∞)
C.(-∞,0)
D.(-∞,0)∪(0,+∞)
答案 A
解析 反函数的定义域即为原函数的值域.由>0可得log2∈R,所以原函数的值域为R,故它的反函数的定义域为R.故选A.
10.已知x>0,f(x)=log3x2的值域是[-1,1],则它的反函数f-1(x)的值域是( )
A.[-1,1]
B.(0,+∞)
C.∪
D.
答案 D
解析 ∵f(x)=log3x2的值域是[-1,1],∴-1≤log3x2≤1,即≤x2≤3,而x>0,∴x∈.∵反函数的值域为原函数的定义域,∴反函数f-1(x)的值域是.
11.如图,已知函数f(x)=3x-1,则它的反函数y=f-1(x)的大致图像是( )
答案 C
解析 由f(x)=3x-1可得f-1(x)=log3x+1,∴图像为C.
12.已知函数y=f(x)的反函数为y=f-1(x),则函数y=f(-x)与y=-f-1(x)的图像( )
A.关于y轴对称
B.关于原点对称
C.关于直线x+y=0对称
D.关于直线x-y=0对称
答案 D
解析 函数y=f(-x)与y=-f-1(x)互为反函数,图像关于直线x-y=0对称.故选D.
13.给出下列命题:
(1)若奇函数存在反函数,则其反函数也是奇函数;
(2)函数f(x)在区间[a,b]上存在反函数的充要条件是f(x)在区间[a,b]上是单调函数;
(3)函数f(x)在定义域D上的反函数为f-1(x),则对于任意的x0∈D都有f(f-1(x0))=f-1(f(x0))=x0成立.
其中正确的命题为( )
A.(1)
B.(1)(2)
C.(1)(3)
D.(1)(2)(3)
答案 A
解析 (1)设奇函数f(x)的反函数为f-1(x),∵f(x)是奇函数,∴f(x)的值域关于原点对称,即f-1(x)的定义域关于原点对称.假设f(x)=y,则f(-x)=-y.∴f-1(y)=x,f-1(-y)=-x.∴f-1(-y)=-f-1(y),即f-1(-x)=-f-1(x).∴f-1(x)是奇函数.故(1)正确;
(2)函数f(x)在区间[a,b]上存在反函数,不一定f(x)在区间[a,b]上是单调函数,
比如f(x)=存在反函数,但f(x)在R上不单调,故(2)不正确;
(3)x0不一定属于f(x)的值域,即f-1(x0)不一定存在,故(3)不正确.故选A.
14.已知点(3,9)在函数f(x)=1+ax的图像上,则f(x)的反函数f-1(x)=________.
答案 log2(x-1)(x>1)
解析 ∵(3,9)在函数f(x)上,∴1+a3=9,解得a=2,∴f(x)=1+2x,又f(x)>1,∴f-1(x)=log2(x-1)(x>1).
15.若函数y=f(x)是函数y=g(x)=a2x的反函数(a>0,且a≠1),且f(4)=1,则a=________.
答案 2
解析 由y=f(x)与y=g(x)互为反函数,且f(4)=1,得g(1)=4,所以a2=4,a=2.
16.若函数y=f(x)的图像过点(0,1),则函数g(x)=f(4-x)的反函数的图像过点________.
答案 (1,4)
解析 ∵y=f(x)的图像过点(0,1),∴f(4-x)的图像过点(4,1),∴g(x)=f(4-x)的反函数的图像过点(1,4).
17.已知f(x)=,其反函数为f-1(x),若f-1(x)-a=f(x+a)有实数根,则a的取值范围为________.
答案
解析 因为y=f-1(x)-a与y=f(x+a)互为反函数,所以二者关于y=x对称.若y=f-1(x)-a与y=f(x+a)有实数根,则y=f(x+a)与y=x有交点,所以=x,即a=x2-x+1=2+≥.
知识点三 指数函数与对数函数的综合应用
18.设a,b,c均为正数,且2a=,b=,c=log2c,则( )
A.a
解析 在同一平面直角坐标系中,画出函数y=2x,y=x,y=log2x,y=的图像,如图所示,则a,b,c分别为两个图像交点的横坐标,根据图像可知a
A.函数f(x)的图像在y轴的一侧
B.函数f(x)为奇函数
C.函数f(x)为定义域上的增函数
D.函数f(x)在定义域内有最大值
答案 AC
解析 ∵函数f(x)=loga(ax-1)(a>0,a≠1),当a>1时,由ax-1>0,可得x>0,此时,函数的图像仅在y轴的右侧;当0
20.已知函数f(x)=log2(1-2x).
(1)求函数f(x)的定义域和值域;
(2)求证函数y=f(x)的图像关于直线y=x对称.
解 (1)要使函数f(x)=log2(1-2x)有意义,
则1-2x>0,即2x<1.
故x<0,此时0<1-2x<1,
∴f(x)=log2(1-2x)<0,
故函数f(x)的定义域为(-∞,0),值域为(-∞,0).
(2)证明:由y=f(x)=log2(1-2x)可得1-2x=2y,解得x=log2(1-2y),故原函数的反函数为f-1(x)=log2(1-2x),与原函数相同,所以函数f(x)的图像关于直线y=x对称.
易错点一 对反函数的定义理解不清而致误
已知函数y=f(x+1)与函数y=g(x)的图像关于直线y=x对称,且g(x)的图像过定点(1,2020),则y=f-1(x+1)的图像过定点________.
易错分析 本题容易误认为f(x+1)与f-1(x+1)互为反函数.
答案 (0,2021)
正解 ∵g(x)的图像过定点(1,2020),
∴f(x+1)的图像过定点(2020,1).
又f(x)的图像可以看作由f(x+1)的图像向右平移一个单位长度得到的,∴f(x)过定点(2021,1).
又f(x)与f-1(x)互为反函数,
∴f-1(x)的图像过定点(1,2021).
再结合f-1(x)与f-1(x+1)的关系可知,
f-1(x+1)的图像过定点(0,2021).
易错点二 不能将问题合理转化致误
设α,β分别是关于x的方程log2x+x-4=0和2x+x-4=0的根,则α+β=________.
易错分析 本题的易错之处为不能正确将问题转化为函数y=log2x,y=2x,y=4-x三个图像之间的关系进行求解.
答案 4
正解 如图,分别作出函数y=log2x,y=2x,y=4-x的图像,相交于点P,Q.∵log2α=4-α,2β=4-β.而y=log2x(x>0)与y=2x互为反函数,直线y=4-x与直线y=x互相垂直,∴点P与Q关于直线y=x对称.
∴α=2β=4-β.∴α+β=4.
一、单项选择题
1.函数y=2x+1(x∈R)的反函数是( )
A.y=1+log2x(x>0)
B.y=log2(x-1)(x>1)
C.y=-1+log2x(x>0)
D.y=log2(x+1)(x>-1)
答案 C
解析 由y=2x+1?x+1=log2y?x=-1+log2y,又因原函数的值域{y|y>0},故其反函数是y=-1+log2x(x>0).
2.把函数y=logax(a>0且a≠1)的图像绕原点逆时针旋转90°后,新图像的函数解析式是( )
A.y=-ax
B.y=a-x
C.y=loga(-x)
D.y=-logax
答案 B
解析 函数的图像绕坐标原点逆时针旋转90°后,得到的函数与原函数的反函数的图像关于y轴对称.函数y=logax(a>0且a≠1)的反函数为y=ax,其关于y轴对称的函数解析式为y=a-x.故选B.
3.已知f(x)=-的反函数为f-1(x)=,则f(x)的定义域为( )
A.(-2,0)
B.[-2,2]
C.[-2,0]
D.[0,2]
答案 D
解析 ∵原函数的定义域就是反函数的值域,原函数的值域就是反函数的定义域.∴解得即0≤x≤2.故f(x)的定义域为[0,2].故选D.
4.当0
B.可能无解
C.可能有3个
D.一定有3个
答案 C
解析 考虑函数y=logax与函数y=ax的图像公共点,易知B,D两项不对.又y=和y=x的图像除了在直线y=x上存在一个公共点外,还存在和两个公共点.故选C.
5.若函数y=ax(a>0,且a≠1)的反函数的图像过点(,a),则a的值为( )
A.2
B.
C.2或
D.3
答案 B
解析 解法一:函数y=ax(a>0,且a≠1)的反函数即y=logax,故y=logax的图像过点(,a),则a=loga=.
解法二:由题意得,函数y=ax(a>0,且a≠1)的反函数的图像过点(,a),则函数y=ax(a>0,且a≠1)的图像过点(a,),即aa==,故a=.
6.函数y=(x≠0)的反函数的图像大致是( )
答案 B
解析 y=(x≠0)的反函数为y=(x≠-1),其图像为y=的图像向左平移1个单位长度.
7.已知函数y=f(x)的定义域是[-1,1],其图像如图所示,则不等式-1≤f-1(x)≤的解集是( )
A.
B.
C.[-2,0)∪
D.[-1,0]∪
答案 C
解析 由题意,可得-1≤f-1(x)≤的解集即为f(x)在上的值域.当-1≤x<0时,由题图可知f(x)∈[-2,0),当0≤x≤时,由题图可知f(x)∈.故不等式-1≤f-1(x)≤的解集为[-2,0)∪.
8.已知函数f(x)=3x,函数g(x)是f(x)的反函数,若正数x1,x2,…,x2020满足x1x2…x2020=81,则g(x)+g(x)+…+g(x)的值等于( )
A.4
B.8
C.16
D.64
答案 B
解析 由函数f(x)=3x,函数g(x)是f(x)的反函数,则g(x)=log3x,所以g(x)+g(x)+…+g(x)=log3(x1x2…x2020)2=2log3(x1x2…x2020)=2log381=8.故选B.
二、多项选择题
9.下列说法中正确的是( )
A.一次函数y=kx+b(k≠0)一定存在反函数
B.若函数f(x)在其定义域内不是单调函数,则f(x)不存在反函数
C.若函数y=f(x)的图像位于第一、二象限,则它的反函数y=f-1(x)的图像位于第一、四象限
D.若函数f(x)存在反函数f-1(x),则f-1(x)与f(x)图像的公共点必在直线y=x上
答案 AC
解析 对于A,一次函数y=kx+b(k≠0)为单调函数,一定存在反函数,故正确;对于B,因为函数f(x)=在定义域上不单调,但函数f(x)存在反函数,故错误;对于C,因为原函数与它的反函数的图像关于y=x对称,所以将y=f(x)的图像沿y=x翻折后,会落在第一、四象限,故正确;对于D,比如函数y=-与其反函数y=x2-1(x≤0)的交点坐标有(-1,0),(0,-1),显然交点不在直线y=x上,故错误.故选AC.
10.在同一直角坐标系下,函数y=ax与y=logax(a>0,a≠1)的大致图像如图所示,则实数a的可能值为( )
A.
B.
C.
D.
答案 BC
解析 由图像可知a>1且a2
11.如果一个点是一个指数函数的图像与一个对数函数的图像的公共点,那么称这个点为“好点”,在下面的四个点中,是“好点”的有( )
A.(1,2)
B.(2,1)
C.(2,2)
D.(2,0.5)
答案 CD
解析 当x=1时,对数函数y=logax(a>0,a≠1)恒过(1,0)点,故(1,2)一定不是好点;当y=1时,指数函数y=ax(a>0,a≠1)恒过(0,1)点,故(2,1)也一定不是好点;而(2,2)是函数y=()x与的交点;(2,0.5)是函数y=x与y=log4x的交点;故选CD.
12.下列说法正确的是( )
A.函数y=ax与y=x图像关于y轴对称
B.函数y=logax与y=图像关于x轴对称
C.函数y=ax与y=logax图像关于直线y=x对称
D.函数y=ax与y=logax图像关于y轴对称
答案 ABC
解析 令a=2,分别作出对应的图像,由图像可知,对于A,∵函数y=ax与y=x图像关于y轴对称,故A正确;对于B,∵函数y=logax与y=图像关于x轴对称,故B正确;对于C,D,∵函数y=ax与y=logax图像关于直线y=x对称,故C正确,D不正确.故选ABC.
三、填空题
13.函数f(x)=-x2(x∈(-∞,-2])的反函数f-1(x)=________.
答案 -,x∈(-∞,-4]
解析 由y=-x2,x∈(-∞,-2],得y∈(-∞,-4],
∴x=-,即f-1(x)=-,x∈(-∞,-4].
14.已知函数f(x)=ax-k的图像过点(1,3),其反函数y=f-1(x)的图像过点(2,0),则f(x)的表达式为________.
答案 f(x)=2x+1
解析 ∵y=f-1(x)的图像过点(2,0),
∴f(x)的图像过点(0,2),∴2=a0-k,∴k=-1,
∴f(x)=ax+1.
又f(x)的图像过点(1,3),
∴3=a1+1,∴a=2,∴f(x)=2x+1.
15.已知函数f(x)与函数g(x)=的图像关于直线y=x对称,则函数f(x2+2x)的单调增区间是________.
答案 (-∞,-1]
解析 由题意得f(x)=x,∴f(x2+2x)=,∵f(x)在R上是减函数,∴由同增异减的原则可知,所求函数的单调增区间即为t=x2+2x的单调减区间,即(-∞,-1].
16.已知函数f(x)=loga(a>0,b≠0),则f(x)的值域为____________,f(x)的反函数f-1(x)的解析式为________________.
答案 (-∞,0)∪(0,+∞) f-1(x)=b·
解析 ∵b≠0,∴≠1,∴f(x)=loga≠0.由y=loga,化为=ay,解得x=b·.把x与y互换可得y=b·,∴f(x)的反函数f-1(x)=b·.
四、解答题
17.若不等式4x-logax<0,当x∈时恒成立,求实数a的取值范围.
解 要使不等式4x<logax在x∈时恒成立,即函数y=logax的图像在内恒在函数y=4x图像的上方,而y=4x的图像过点.
由图可知,loga≥2,显然这里0<a<1,
∴函数y=logax递减.
又loga≥2=logaa2,∴a2≥,
又0
18.已知f(x)=,求f-1的值.
解 令y=,∴y+y·3x=1-3x,∴3x=,
∴x=log3,∴f-1(x)=log3.
∴f-1=log3=log3=-2.
19.已知y=f(x)是R上的增函数,点A(-1,1),B(1,3)在它的图像上,y=f-1(x)是它的反函数,解不等式|f-1(log2x)|<1.
解 ∵y=f(x)是R上的增函数,
∴y=f-1(x)在R上也是增函数.
∵f(-1)=1,f(1)=3,∴f-1(1)=-1,f-1(3)=1.
由|f-1(log2x)|<1,得-1
(1)求a的值,并判断f(x)的奇偶性;
(2)求f(x)的反函数;
(3)对任意的k∈(0,+∞),解不等式f-1(x)>log2.
解 (1)由f(0)=0,得a=1,所以f(x)=(x∈R).
因为f(x)+f(-x)=+=+=0,
所以f(-x)=-f(x),即f(x)为奇函数.
(2)因为f(x)=y==1-,
所以2x=(-1<y<1),
所以f-1(x)=log2(-1<x<1).
(3)因为f-1(x)>log2,
即log2>log2,所以
所以
当0<k<2时,原不等式的解集为{x|1-k<x<1};
当k≥2时,原不等式的解集为{x|-1<x<1}.
