第14章统计 综合提升测试-【新教材】2020-2021学年苏教版(2019)高中数学必修第二册(Word含解析)
文档属性
| 名称 | 第14章统计 综合提升测试-【新教材】2020-2021学年苏教版(2019)高中数学必修第二册(Word含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-18 10:39:21 | ||
图片预览




文档简介
苏教版第14章统计综合提升测试卷
一、单选题
1.小华同学每天晚上睡觉前要求自己背诵15个英文单词,若将超出记为“+”,不足记为“-”,则上周一至周五,他的完成情况分别为-2,-1,,+4,,已知这五个数据的平均数是0,方差是5.2,则上周一至周五,小华背诵的单词数量的众数和中位数分别是( )
A.13,14 B.-2,-1 C.13,13 D.-2,-2
2.每年的3月15日是“国际消费者权益日”,某地市场监管局在当天对某市场的20家肉制品店、100家粮食加工品店和15家乳制品店进行抽检,要用分层抽样的方法从中抽检27家,则粮食加工品店需要被抽检( )
A.20家 B.10家 C.15家 D.25家
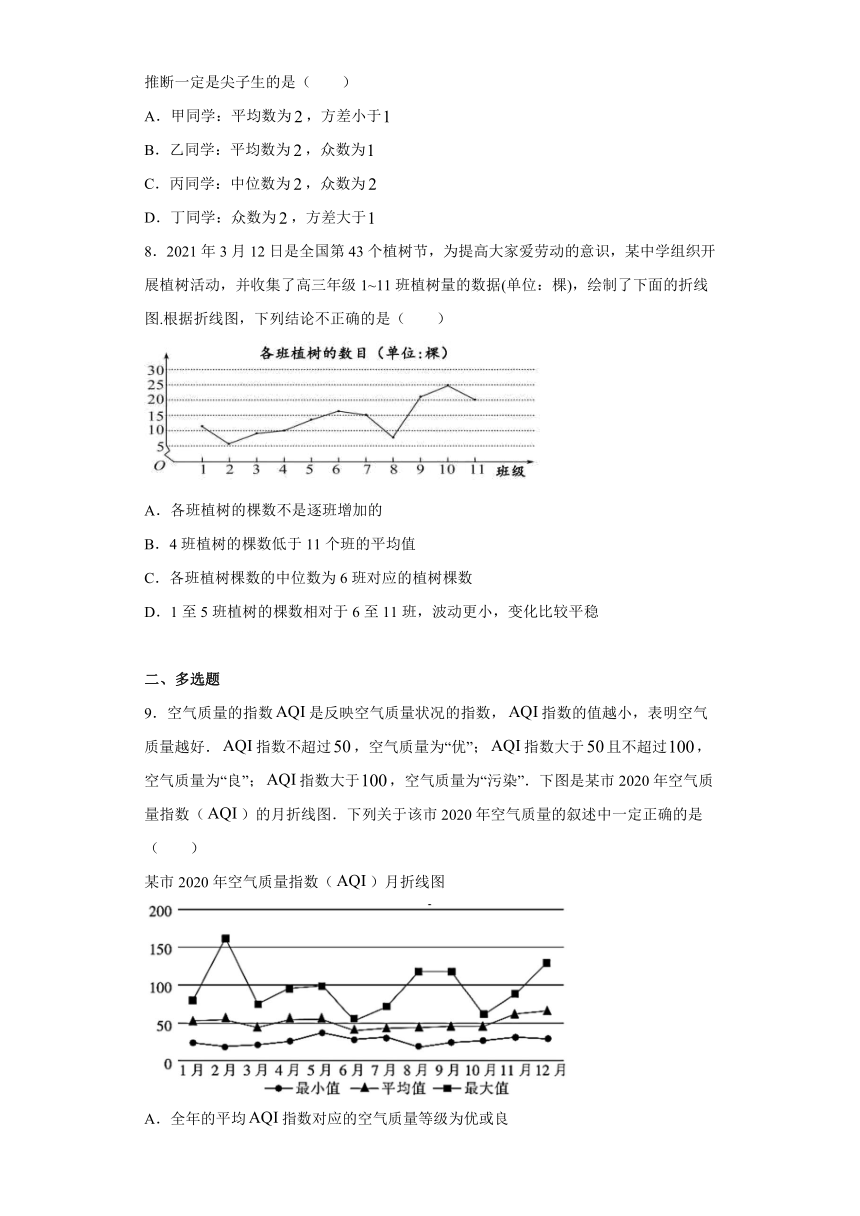
3.恩格尔系数(Engel’sCoefficien)是食品支出总额占个人消费支出总额的比重.居民可支配收入是居民可用于最终消费支出和储蓄的总和,即居民可用于自由支配的收入.如图为我国2013年至2019年全国恩格尔系数和居民人均可支配收入的折线图.
给出三个结论:
①恩格尔系数与居民人均可支配收入之间存在负相关关系;
②一个国家的恩格尔系数越小,说明这个国家越富裕;
③一个家庭收入越少,则家庭收入中用来购买食品的支出所占的比重就越小.
其中正确的是( )
A.① B.② C.①② D.②③
4.将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91.现场作的9个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x表示:
则7个剩余分数的方差为( )
A. B. C.36 D.
5.某赛季甲乙两名篮球运动员在若干场比赛中的得分情况如下:
甲:21、22、23、25、28、29、30、30;
乙:14、16、23、26、28、30、33、38.
则下列描述合理的是( )
A.甲队员每场比赛得分的平均值大 B.乙队员每场比赛得分的平均值大
C.甲队员比赛成绩比较稳定 D.乙队员比赛成绩比较稳定
6.某校通过问卷调查了解500名学生周末参加体育锻炼的时间,频率分布直方图如下图所示,数据的分组依次为:, 则在调查的学生中周末参加体育锻炼的时间不少于60分钟的人数是( )
A.125 B.175 C.200 D.300
7.若某同学连续次考试的名次(次考试均没有出现并列名次的情况)不低于第名,则称该同学为班级的尖子生.根据甲、乙、丙、丁四位同学过去连续次考试名次的数据,推断一定是尖子生的是( )
A.甲同学:平均数为,方差小于
B.乙同学:平均数为,众数为
C.丙同学:中位数为,众数为
D.丁同学:众数为,方差大于
8.2021年3月12日是全国第43个植树节,为提高大家爱劳动的意识,某中学组织开展植树活动,并收集了高三年级1~11班植树量的数据(单位:棵),绘制了下面的折线图.根据折线图,下列结论不正确的是( )
A.各班植树的棵数不是逐班增加的
B.4班植树的棵数低于11个班的平均值
C.各班植树棵数的中位数为6班对应的植树棵数
D.1至5班植树的棵数相对于6至11班,波动更小,变化比较平稳
二、多选题
9.空气质量的指数是反映空气质量状况的指数,指数的值越小,表明空气质量越好.指数不超过,空气质量为“优”;指数大于且不超过,空气质量为“良”;指数大于,空气质量为“污染”.下图是某市2020年空气质量指数()的月折线图.下列关于该市2020年空气质量的叙述中一定正确的是( )
某市2020年空气质量指数()月折线图
A.全年的平均指数对应的空气质量等级为优或良
B.每月都至少有一天空气质量为优
C.2月,8月,9月和12月均出现污染天气
D.空气质量为“污染”的天数最多的月份是2月份
10.在第一次全市高三年级统考后,某数学老师为了解本班学生的本次数学考试情况,将全班50名学生的数学成绩绘制成频率分布直方图.已知该班级学生的数学成绩全部介于65到145之间(满分150分),将数学成绩按如下方式分成八组:第一组,第二组,…,第八组,按上述分组方法得到的频率分布直方图的一部分,如图所示,则下列结论正确的是( )
A.第七组的频率为0.008
B.该班级数学成绩的中位数的估计值为101
C.该班级数学成绩的平均分的估计值大于95
D.该班级数学成绩的方差的估计值大于26
11.气象意义上从春季进入夏季的标志为:“连续5天日平均温度不低于22℃”.现有甲、乙、丙三地连续5天日平均温度的记录数据(数据都是正整数,单位℃)满足以下条件:
甲地:5个数据的中位数是24,众数是22;
乙地:5个数据的中位数是27,平均数是24;
丙地:5个数据有1个是32,平均数是26,方差是10.2.
则下列说法正确的是( )
A.进入夏季的地区有2个 B.丙地区肯定进入了夏季
C.乙地区肯定还未进入夏季 D.不能肯定甲地区进入了夏季
12.动力电池组对新能源汽车的性能表现以及安全性影响巨大,是新能源汽车非常核心的部件.如图是刀片电池、三元锂电池和磷酸铁锂电池部分指标的雷达图,则下列说法正确的是( )
A.刀片电池的安全性更高,价格优势更突出
B.三元锂电池的缺点是循环寿命较短、价格偏高、安全性偏低
C.对于这7项指标,刀片电池的平均得分低于三元锂电池
D.磷酸铁锂电池能量密度低、低温性能好
三、填空题
13.一个容量为n的样本,分成若干组,已知某组的频数和频率分别为50和0.25,则n=________.
14.某兄弟俩都推销某一小家电,现抽取他们其中8天的销售量(单位:台),得到的茎叶图如图所示,已知弟弟的销售量的平均数为34,哥哥的销售量的中位数比弟弟的销售量的众数大2,则x+y的值为___________.
15.某社会爱心组织面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取名按年龄分组:第组,第组,第组,第组,第组,得到的频率分布直方图如图所示.若从第,,组中用分层抽样的方法抽取名志愿者参与广场的宣传活动,应从第组抽取__________名志愿者.
16.为了解中学生课外阅读情况,现从某中学随机抽取名学生,收集了他们一年内的课外阅读量(单位:本)等数据,以下是根据数据绘制的统计图表的一部分.
下面有四个推断:
①这名学生阅读量的平均数可能是本;
②这名学生阅读量的分位数在区间内;
③这名学生中的初中生阅读量的中位数一定在区间内;
④这名学生中的初中生阅读量的分位数可能在区间内.
所有合理推断的序号是________.
四、解答题
17.从某歌唱比赛中抽取若干名选手的参赛成绩,绘制成如下的频率分布直方图.
(1)求这些选手的平均成绩(同一组中数据用该组区间中点作代表);
(2)求这些选手的成绩的中位数.(精确到0.1)
18.某地区拟举办汉字听写大赛,某校为了选拔优秀的学生参加比赛,在本校举行了次汉字听写大赛,其中甲、乙两位同学的成绩最优异,由甲、乙两位同学的成绩绘制的茎叶图如图所示.已知甲成绩的中位数小于乙成绩的中位数.
(1)求的值;
(2)若要从甲、乙中选择一名同学参加该地区举办的汉字听写大赛,试从统计学的角度分析,选哪位同学比较合适.
19.某网络营销部门随机抽查了某市200名网友在2019年11月11日的网购金额,所得数据如下表:
网购金额(单位:千元) 人数 频率
[0,1) 16 0.08
[1,2) 24 0.12
[2,3) x p
[3,4) y q
[4,5) 16 0.08
[5,6] 14 0.07
合计 200 1.00
已知网购金额低于3千元与不低于3千元的人数比恰为3∶2.
(1)试确定x,y,p,q的值,并补全频率直方图;
(2)估计网购金额的25百分位数(结果保留3位有效数字).
20.某校高三文科名学生参加了月的模拟考试,学校为了了解高三文科学生的数学、外语成绩情况,利用随机数表法从中抽取名学生的成绩进行统计分析,将学生编号为、、、….
(1)若从第行第列的数开始右读,请你依次写出最先抽出的人的编号(下面是摘自随机数表的第行至第行);
(2)抽出的名学生的数学、外语成绩如表:
外语
优 良 及格
数学 优
良
及格
若数学成绩优秀率为,求、的值;
(3)在外语成绩为良的学生中,已知,,求数学成绩优比良的人数少的概率.
21.某次人才招聘活动中,某公司计划招收600名新员工.由于报名者共2000人,远超计划,故该公司采用笔试的方法进行选拔,并按照笔试成绩择优录取.现采用随机抽样的方法抽取200名报名者的笔试成绩,绘制频率分布直方图如下:
已知直方图中,左边四个小长方形的高度自左向右依次构成公比为2的等比数列.根据频率分布直方图解答以下问题:
(1)求;
(2)估计此次笔试的平均成绩;
(3)估计该公司此次招聘的录取分数线.
22.企业在商业活动中有依法纳税的基本义务,不依法纳税叫做逃税,是一种违法行为.某地区有2万家企业,政府部门抽取部分企业统计其去年的收入,得到下面的频率分布表.根据当地政策综合测算,企业应缴的税额约为收入的5%,而去年该地区企业实际缴税的总额为291亿元.
收入(千万元)
频率 0.3 0.5 0.12 0.06 0.02
(1)估计该地区去年收入大于等于4千万元的企业数量;
(2)估计该地区企业去年的平均收入,并以此估计该地区逃税的企业数量;
(3)根据统计,该地区企业逃税被查出来的概率为0.3,被查出逃税的企业除了要补缴税款以外,还会被处以应缴税额倍的罚款,从企业逃税的获益期望考虑,至少定为多少,才能对逃税行为起到惩罚作用?
注:每组数据以区间中点值为代表,假设逃税的企业缴税额为0,未逃税的企业都足额缴税.
参考答案
1.A
【分析】
由平均数和方差可以求出,,从而就可以得到众数和中位数.
【详解】
因为-2,-1,,+4,,已知这五个数据的平均数是0,方差是5.2,
所以有,解得或,不管取哪一组解,这5天的单词量是以下几个数,
13,14,13,19,16,
所以众数和中位数分别是13,14.
故选:A.
2.A
【分析】
确定抽样比,即可得到结果.
【详解】
解:根据分层抽样原理知,粮食加工品店需要被抽检(家).
故选:A.
3.C
【分析】
通过对2013年至2019年全国恩格尔系数和居民人均可支配收入的折线图的分析,了解两者间的相关性而作出判断.
【详解】
由折线图可知,恩格尔系数在逐年下降,居民人均可支配收入在逐年增加,
故两者之间存在负相关关系,结论①正确;
恩格尔系数越小,居民人均可支配收入越多,经济越富裕,结论②正确;
家庭收入越少,人们为解决温饱问题,收入的大部分用来购买食品,结论③错误.
故选:C
4.B
【分析】
根据茎叶图中的数据,去掉最大值和最小值,然后计算平均值,从而求得x,按照方差公式计算方差即可.
【详解】
由图可知去掉的两个数是87,99,
所以87+90×2+91×2+94+90+x=91×7,解得x=4.
故方差为:s2=[(87-91)2+(90-91)2×2+(91-91)2×2+(94-91)2×2]=.
故选:B.
5.C
【分析】
计算均值,再根据数据的集中度判断.
【详解】
甲的均值为,
乙的均值为,
两者均值相同,甲的方差为
乙的方差为
,
甲的方差小于乙的方差,甲稳定.
故选:C.
6.C
【分析】
求出的频率,可得周末参加体育锻炼的时间不少于60分钟的频率,即可求解.
【详解】
设周末参加体育锻炼的时间在的频率为,
则由频率分布直方图可知,,
解得,
所以周末参加体育锻炼的时间不少于60分钟的频率为
所以周末参加体育锻炼的时间不少于60分钟的人数人.
故选:C
7.A
【分析】
根据定义,结合各组的情况,举出特例排除错误选项;对正确选项,计算即可做出判断.
【详解】
对于甲同学,平均数为,方差小于,设甲同学三次考试的名次分别为、、,
若、、中至少有一个大于等于,则方差为,与已知条件矛盾,
所以,、、均不大于,满足题意;
对于乙同学,平均数为,众数为,则三次考试的成绩的名次为、、,
即必有一次考试为第名,不满足题意;
对于丙同学,中位数为,众数为,可举反例:、、,不满足题意;
对于丁同学,众数为,方差大于,可举特例:、、,则平均数为,
方差为,不满足条件.
故选:A.
【点睛】
关键点点睛:解决本题的关键在于以下两点:
(1)在判断选项不成立时,可通过举反例来否定;
(2)在判断A选项时,可、、中至少有一个大于或等于,利用反证法来推导.
8.C
【分析】
从图中直接观察可以判定AD正确,结合平均数的定义,将比4班多的里面取出部分补到比4班少的班中,可以使得4班的植树量最少,从而判定B正确;结合中位数的定义可以判定C错误.
【详解】
从图可知,2班的植树量少于1班,8班的植树量少于7班,故A正确;
4班的指数棵数为10,11个班中只有2、3、8班三个的植树棵数少于10,且大于5棵,其余7个班的植树棵数都超过10棵,且有6、7、9、10、11班五个班的植树棵数都不少于15棵,将这五个班中的植树棵数各取出5棵,加到2、3、8班中取,除4班外,其余各班的植树棵数都超过了4班,所以4班植树的棵数低于11个班的平均值,故B正确;
比6班植树多的只有9、10、11三个班,其余七个班都比6班少,故6班所对应的植树棵数不是中位数,故C是错误的;
1到5班的植树棵数的极差在10以内,6到11班的植树棵数的极差超过了15,另外从图明显看出,1至5班植树的棵数相对于6至11班,波动更小,变化比较平稳,故D正确;
综上,不正确的只有C,
故选:C.
【点睛】
本题考查频数折线图的意义,涉及平均数,中位数,波动大小的判定,难点是平均数的估算,这里采用取长补短法进行估算,可以避免数字的计算.
9.ABC
【分析】
根据空气质量指数()的月折线图逐一判断即可.
【详解】
每月的平均指数都不超过,故全年的平均指数也不超过,对应的空气质量为优或良,故选项A正确;每月的指数最小值均不超过,故每月都至少有一天空气质量为优,选项B正确;2月,8月,9月和12月的指数最大值均大于,故至少有一天出现了污染天气,故选项C正确;2月,8月,9月,12月中空气质量为“污染”的天数不确定,故选项D不一定正确,
故选:ABC
10.BCD
【分析】
由频率直方图中的数据,根据频率之和为1直接求第七组的频率,由中位数、平均数、方差的求法,判断判断各项的正误.
【详解】
A:设第七组的频率为,则,得,错误;
B:由知:中位数在区间,若中位数为,则:,解得,正确;
C:由图知:,正确;
D:,正确;
故选:BCD.
11.ABC
【分析】
根据中位数、平均数,方差判断三地数据中最低的温度是否低于22℃,即可得.
【详解】
甲地:设甲地的其他两个数据分别为,,且,将5个数据由小到大排列得22,22,24,,,其中,满足进入夏季的标志;
乙地:设乙地其他四个数据分别为,,,,且,将5个数据由小到大排列得,,27,,,则,而,故,其中必有一个小于22,故不满足进入夏季的标志;
丙地:设5个数据分别为,,,,32,且,由方差公式可知,则
,易知,,,均大于22,满足进入夏季的标志综上,ABC正确,
故选:ABC.
12.AB
【分析】
借助于雷达图分析数据,对A、B、C、D一一验证即可.
【详解】
由雷达图易知刀片电池的安全性更高,价格优势更突出,A正确;
三元锂电池的循环寿命较短、价格偏高、安全性偏低,B正确;
对于这7项指标,刀片电池的平均得分为,三元锂电池的平均得分为,所以C错误;
磷酸铁锂电池能量密度低、低温性能差,D错误.
故选:AB
13.200
【分析】
根据频率公式求解.
【详解】
∵,
∴,
故答案为:200
14.13
【分析】
先根据弟弟的销售量的平均数为34,求得y,进而得到其众数,然后再根据哥哥的销售量的中位数比弟弟的销售量的众数大2,得到哥哥的销售量的中位数求解.
【详解】
因为弟弟的销售量的平均数为34,
所以,
解得,
由茎叶图知:弟弟的销售量的众数是34,
因为哥哥的销售量的中位数比弟弟的销售量的众数大2,
所以哥哥的销售量的中位数是36,
所以,解得,
所以,
故答案为:13
15.
【分析】
先分别求出这3组的人数,再利用分层抽样的方法即可得出答案.
【详解】
第3组的人数为,
第4组的人数为,
第5组的人数为,
所以这三组共有60名志愿者,
所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,第三组应抽取名,
故答案为:3.
【点睛】
关键点点睛:该题考查的是有关频率分布直方图的识别以及分层抽样某层抽取个数的问题,正确解题的关键是掌握在抽取过程中每个个题被抽到的机会均等.
16.②③④
【分析】
①由学生类别阅读量图表可知;
②计算75%分位数的位置,在区间内查人数即可;
③设在区间内的初中生人数为,则,分别计算为最大值和最小值时的中位数位置即可;
④设在区间内的初中生人数为,则,分别计算为最大值和最小值时的25%分位数位置即可.
【详解】
在①中,由学生类别阅读量中男生和女生人均阅读量知,这200名学生的平均阅读量在区间内,故错误;
在②中,,阅读量在的人数有人,
在的人数有62人,所以这200名学生阅读量的75%分位数在区间内,
故正确;
在③中,设在区间内的初中生人数为,则,
当时,初中生总人数为116人,,
此时区间有25人,区间有36人,所以中位数在内,
当时,初中生总人数为131人,,
区间有人,区间有36人,所以中位数在内,
当区间人数去最小和最大,中位数都在内,
所以这名学生中的初中生阅读量的中位数一定在区间内,故正确;
在④中,设在区间内的初中生人数为,则,
当时,初中生总人数为116人,,
此时区间有25人,区间有36人,所以25%分位数在内,
当时,初中生总人数为131人,,
区间有人,所以25%分位数在内,
所以这名学生中的初中生阅读量的25%分位数可能在区间内,故正确;
故答案为:②③④
【点睛】
本题主要考查频数分布表、平均数和分位数的计算,考查学生对参数的讨论以及计算能力,属于中档题.
17.(1)10.1分;(2)10.3.
【分析】
(1)由频率直方图,根据平均数计算方法可得答案;
(2)根据中位数的计算方法可得答案.
【详解】
解:(1)由题意,得
中间值 5 7 9 11 13 15
频率 0.1 0.15 0.2 0.3 0.15 0.1
所以
所以这些选手的平均成绩为10.1分.
(2)设这些选手的成绩的中位数为y,
因为,
所以.
所以,则,
故这些选手的成绩的中位数为10.3.
【点睛】
本题考查根据频率直方图求得平均数和中位数,属于基础题.
18.(1)0;(2)乙同学比较合适.
【分析】
(1)由乙的中位数为91,甲的中位数(90+x)小于91得解;
(2)计算甲乙二人三次成绩的平均数、方差等特征数据,再分析选择.
【详解】
(1)由茎叶图可知,乙同学成绩的中位数为.
又由茎叶图可得甲同学成绩的中位数大于或等于,
且甲成绩的中位数小于乙成绩的中位数,所以甲同学成绩的中位数只能为,
故.
(2)甲同学成绩的平均数为,
乙同学成绩的平均数为,
所以甲、乙成绩的平均数相等.
甲同学成绩的方差,
乙同学成绩的方差,
,所以乙同学的成绩更稳定,选乙同学比较合适.
19.(1),p=0.4,q=0.25,直方图见解析;(2)2.13(千元).
【分析】
(1)根据已知条件列出关于的方程组,解之可得,然后由频率公式计算出,补全直方图;
(2)求出网购金额低于2千元的频率为0.2,网购金额低于3千元的频率为0.6,得出网购金额的25百分位数在[2,3)内,利用比例可得.
【详解】
解 (1)根据题意有
解得
所以p=0.4,q=0.25.
补全频率直方图如图所示.
(2)由(1)可知,网购金额低于2千元的频率为0.08+0.12=0.2,
网购金额低于3千元的频率为0.2+0.4=0.6,
所以网购金额的25百分位数在[2,3)内,
则网购金额的25百分位数估计为2+×1=2+0.125≈2.13(千元).
20.(1)、、、、;(2),;(3).
【分析】
(1)由学生编号为、、、…,从第行第列的数开始右读,有943、949、、、、、、、、、、、…,根据编号规则确认符合要求的前5个数字即为所得.
(2)根据表格数据,有,即可求m、n;
(3)由题设知:且,,列举法写出所有可能组合情况,以及数学成绩优比良的人数少的组合情况,求概率.
【详解】
(1)根据图表数据,结合编号规则知:最先抽出的人的编号依次为、、、、;
(2)由,得,
∵,
∴;
(3),且,,
∴满足条件的有:、、、、、、、
、、、、、、共有种,且每组出现都是等可能的,
记:“数学成绩优秀的人数比良的人数少”为事件,事件包括:、、、、、共个基本事件,
∴.
21.(1) (2)67.1 (3)75
【分析】
(1)先求出成绩在30到70的频率为0.6,然后根据条件列出方程求解即可.
(2)先求出成绩在各段的频率,由求平均数的公式可得答案.
(3)先求出录取的频率为0.3,从由右到左求出频率为0.3的点即可.
【详解】
(1)笔试成绩在30到70的频率为
由左边四个小长方形的高度自左向右依次构成公比为2的等比数列,分别设为
所以,解得
所以
(2)成绩在各段的频率分布为:
平均值为:
(3)由于报名者共2000人,计划招收600名新员工,则
由成绩在80到100的频率为.
由于成绩在70到80之间的频率为0.2
所以被录取的分数在70到80之间的频率应为0.1,故录取成绩分数为75.
22.(1)4000;(2)平均收入的估计值为3(千万元);逃税的企业数量为600;(3)至少定为3.
【分析】
(1)先根据表格计算收入大于等于4千万元的频率,再计算企业数量;(2)首先计算平均收入的估计值,再计算平均缴税额,再根据实际缴税总额,计算缴税企业的数量,即可得逃税的企业数量;(3)首先求企业逃税的获利收益的分布列,再求期望,令期望小于0,即可求得的最小值.
【详解】
(1)去年收入大于等于4千万元的频率为,
所以估计该地区去年收入大于等于4千万元的企业数量为.
(2)该地区企业去年的平均收入的估计值为
(千万元).
平均缴税额为(千万元)(亿元),
所以未逃税的企业数量为,
因此,逃税的企业数量为.
(3)设企业应缴税额为,企业逃税的获益为,
若该企业逃税未被查出,则;
若该企业逃税被查出来,则.
由条件知,,
所以,
要对逃税行为起到惩罚作用,则需,解得.
所以至少定为3,才能对逃税行为起到惩罚作用.
【点睛】
关键点点睛:本题考查离散型变量的分布列和数学期望,以及解决实际问题,本题的关键是理解题意,并能转化为数学问题.
一、单选题
1.小华同学每天晚上睡觉前要求自己背诵15个英文单词,若将超出记为“+”,不足记为“-”,则上周一至周五,他的完成情况分别为-2,-1,,+4,,已知这五个数据的平均数是0,方差是5.2,则上周一至周五,小华背诵的单词数量的众数和中位数分别是( )
A.13,14 B.-2,-1 C.13,13 D.-2,-2
2.每年的3月15日是“国际消费者权益日”,某地市场监管局在当天对某市场的20家肉制品店、100家粮食加工品店和15家乳制品店进行抽检,要用分层抽样的方法从中抽检27家,则粮食加工品店需要被抽检( )
A.20家 B.10家 C.15家 D.25家
3.恩格尔系数(Engel’sCoefficien)是食品支出总额占个人消费支出总额的比重.居民可支配收入是居民可用于最终消费支出和储蓄的总和,即居民可用于自由支配的收入.如图为我国2013年至2019年全国恩格尔系数和居民人均可支配收入的折线图.
给出三个结论:
①恩格尔系数与居民人均可支配收入之间存在负相关关系;
②一个国家的恩格尔系数越小,说明这个国家越富裕;
③一个家庭收入越少,则家庭收入中用来购买食品的支出所占的比重就越小.
其中正确的是( )
A.① B.② C.①② D.②③
4.将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91.现场作的9个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x表示:
则7个剩余分数的方差为( )
A. B. C.36 D.
5.某赛季甲乙两名篮球运动员在若干场比赛中的得分情况如下:
甲:21、22、23、25、28、29、30、30;
乙:14、16、23、26、28、30、33、38.
则下列描述合理的是( )
A.甲队员每场比赛得分的平均值大 B.乙队员每场比赛得分的平均值大
C.甲队员比赛成绩比较稳定 D.乙队员比赛成绩比较稳定
6.某校通过问卷调查了解500名学生周末参加体育锻炼的时间,频率分布直方图如下图所示,数据的分组依次为:, 则在调查的学生中周末参加体育锻炼的时间不少于60分钟的人数是( )
A.125 B.175 C.200 D.300
7.若某同学连续次考试的名次(次考试均没有出现并列名次的情况)不低于第名,则称该同学为班级的尖子生.根据甲、乙、丙、丁四位同学过去连续次考试名次的数据,推断一定是尖子生的是( )
A.甲同学:平均数为,方差小于
B.乙同学:平均数为,众数为
C.丙同学:中位数为,众数为
D.丁同学:众数为,方差大于
8.2021年3月12日是全国第43个植树节,为提高大家爱劳动的意识,某中学组织开展植树活动,并收集了高三年级1~11班植树量的数据(单位:棵),绘制了下面的折线图.根据折线图,下列结论不正确的是( )
A.各班植树的棵数不是逐班增加的
B.4班植树的棵数低于11个班的平均值
C.各班植树棵数的中位数为6班对应的植树棵数
D.1至5班植树的棵数相对于6至11班,波动更小,变化比较平稳
二、多选题
9.空气质量的指数是反映空气质量状况的指数,指数的值越小,表明空气质量越好.指数不超过,空气质量为“优”;指数大于且不超过,空气质量为“良”;指数大于,空气质量为“污染”.下图是某市2020年空气质量指数()的月折线图.下列关于该市2020年空气质量的叙述中一定正确的是( )
某市2020年空气质量指数()月折线图
A.全年的平均指数对应的空气质量等级为优或良
B.每月都至少有一天空气质量为优
C.2月,8月,9月和12月均出现污染天气
D.空气质量为“污染”的天数最多的月份是2月份
10.在第一次全市高三年级统考后,某数学老师为了解本班学生的本次数学考试情况,将全班50名学生的数学成绩绘制成频率分布直方图.已知该班级学生的数学成绩全部介于65到145之间(满分150分),将数学成绩按如下方式分成八组:第一组,第二组,…,第八组,按上述分组方法得到的频率分布直方图的一部分,如图所示,则下列结论正确的是( )
A.第七组的频率为0.008
B.该班级数学成绩的中位数的估计值为101
C.该班级数学成绩的平均分的估计值大于95
D.该班级数学成绩的方差的估计值大于26
11.气象意义上从春季进入夏季的标志为:“连续5天日平均温度不低于22℃”.现有甲、乙、丙三地连续5天日平均温度的记录数据(数据都是正整数,单位℃)满足以下条件:
甲地:5个数据的中位数是24,众数是22;
乙地:5个数据的中位数是27,平均数是24;
丙地:5个数据有1个是32,平均数是26,方差是10.2.
则下列说法正确的是( )
A.进入夏季的地区有2个 B.丙地区肯定进入了夏季
C.乙地区肯定还未进入夏季 D.不能肯定甲地区进入了夏季
12.动力电池组对新能源汽车的性能表现以及安全性影响巨大,是新能源汽车非常核心的部件.如图是刀片电池、三元锂电池和磷酸铁锂电池部分指标的雷达图,则下列说法正确的是( )
A.刀片电池的安全性更高,价格优势更突出
B.三元锂电池的缺点是循环寿命较短、价格偏高、安全性偏低
C.对于这7项指标,刀片电池的平均得分低于三元锂电池
D.磷酸铁锂电池能量密度低、低温性能好
三、填空题
13.一个容量为n的样本,分成若干组,已知某组的频数和频率分别为50和0.25,则n=________.
14.某兄弟俩都推销某一小家电,现抽取他们其中8天的销售量(单位:台),得到的茎叶图如图所示,已知弟弟的销售量的平均数为34,哥哥的销售量的中位数比弟弟的销售量的众数大2,则x+y的值为___________.
15.某社会爱心组织面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取名按年龄分组:第组,第组,第组,第组,第组,得到的频率分布直方图如图所示.若从第,,组中用分层抽样的方法抽取名志愿者参与广场的宣传活动,应从第组抽取__________名志愿者.
16.为了解中学生课外阅读情况,现从某中学随机抽取名学生,收集了他们一年内的课外阅读量(单位:本)等数据,以下是根据数据绘制的统计图表的一部分.
下面有四个推断:
①这名学生阅读量的平均数可能是本;
②这名学生阅读量的分位数在区间内;
③这名学生中的初中生阅读量的中位数一定在区间内;
④这名学生中的初中生阅读量的分位数可能在区间内.
所有合理推断的序号是________.
四、解答题
17.从某歌唱比赛中抽取若干名选手的参赛成绩,绘制成如下的频率分布直方图.
(1)求这些选手的平均成绩(同一组中数据用该组区间中点作代表);
(2)求这些选手的成绩的中位数.(精确到0.1)
18.某地区拟举办汉字听写大赛,某校为了选拔优秀的学生参加比赛,在本校举行了次汉字听写大赛,其中甲、乙两位同学的成绩最优异,由甲、乙两位同学的成绩绘制的茎叶图如图所示.已知甲成绩的中位数小于乙成绩的中位数.
(1)求的值;
(2)若要从甲、乙中选择一名同学参加该地区举办的汉字听写大赛,试从统计学的角度分析,选哪位同学比较合适.
19.某网络营销部门随机抽查了某市200名网友在2019年11月11日的网购金额,所得数据如下表:
网购金额(单位:千元) 人数 频率
[0,1) 16 0.08
[1,2) 24 0.12
[2,3) x p
[3,4) y q
[4,5) 16 0.08
[5,6] 14 0.07
合计 200 1.00
已知网购金额低于3千元与不低于3千元的人数比恰为3∶2.
(1)试确定x,y,p,q的值,并补全频率直方图;
(2)估计网购金额的25百分位数(结果保留3位有效数字).
20.某校高三文科名学生参加了月的模拟考试,学校为了了解高三文科学生的数学、外语成绩情况,利用随机数表法从中抽取名学生的成绩进行统计分析,将学生编号为、、、….
(1)若从第行第列的数开始右读,请你依次写出最先抽出的人的编号(下面是摘自随机数表的第行至第行);
(2)抽出的名学生的数学、外语成绩如表:
外语
优 良 及格
数学 优
良
及格
若数学成绩优秀率为,求、的值;
(3)在外语成绩为良的学生中,已知,,求数学成绩优比良的人数少的概率.
21.某次人才招聘活动中,某公司计划招收600名新员工.由于报名者共2000人,远超计划,故该公司采用笔试的方法进行选拔,并按照笔试成绩择优录取.现采用随机抽样的方法抽取200名报名者的笔试成绩,绘制频率分布直方图如下:
已知直方图中,左边四个小长方形的高度自左向右依次构成公比为2的等比数列.根据频率分布直方图解答以下问题:
(1)求;
(2)估计此次笔试的平均成绩;
(3)估计该公司此次招聘的录取分数线.
22.企业在商业活动中有依法纳税的基本义务,不依法纳税叫做逃税,是一种违法行为.某地区有2万家企业,政府部门抽取部分企业统计其去年的收入,得到下面的频率分布表.根据当地政策综合测算,企业应缴的税额约为收入的5%,而去年该地区企业实际缴税的总额为291亿元.
收入(千万元)
频率 0.3 0.5 0.12 0.06 0.02
(1)估计该地区去年收入大于等于4千万元的企业数量;
(2)估计该地区企业去年的平均收入,并以此估计该地区逃税的企业数量;
(3)根据统计,该地区企业逃税被查出来的概率为0.3,被查出逃税的企业除了要补缴税款以外,还会被处以应缴税额倍的罚款,从企业逃税的获益期望考虑,至少定为多少,才能对逃税行为起到惩罚作用?
注:每组数据以区间中点值为代表,假设逃税的企业缴税额为0,未逃税的企业都足额缴税.
参考答案
1.A
【分析】
由平均数和方差可以求出,,从而就可以得到众数和中位数.
【详解】
因为-2,-1,,+4,,已知这五个数据的平均数是0,方差是5.2,
所以有,解得或,不管取哪一组解,这5天的单词量是以下几个数,
13,14,13,19,16,
所以众数和中位数分别是13,14.
故选:A.
2.A
【分析】
确定抽样比,即可得到结果.
【详解】
解:根据分层抽样原理知,粮食加工品店需要被抽检(家).
故选:A.
3.C
【分析】
通过对2013年至2019年全国恩格尔系数和居民人均可支配收入的折线图的分析,了解两者间的相关性而作出判断.
【详解】
由折线图可知,恩格尔系数在逐年下降,居民人均可支配收入在逐年增加,
故两者之间存在负相关关系,结论①正确;
恩格尔系数越小,居民人均可支配收入越多,经济越富裕,结论②正确;
家庭收入越少,人们为解决温饱问题,收入的大部分用来购买食品,结论③错误.
故选:C
4.B
【分析】
根据茎叶图中的数据,去掉最大值和最小值,然后计算平均值,从而求得x,按照方差公式计算方差即可.
【详解】
由图可知去掉的两个数是87,99,
所以87+90×2+91×2+94+90+x=91×7,解得x=4.
故方差为:s2=[(87-91)2+(90-91)2×2+(91-91)2×2+(94-91)2×2]=.
故选:B.
5.C
【分析】
计算均值,再根据数据的集中度判断.
【详解】
甲的均值为,
乙的均值为,
两者均值相同,甲的方差为
乙的方差为
,
甲的方差小于乙的方差,甲稳定.
故选:C.
6.C
【分析】
求出的频率,可得周末参加体育锻炼的时间不少于60分钟的频率,即可求解.
【详解】
设周末参加体育锻炼的时间在的频率为,
则由频率分布直方图可知,,
解得,
所以周末参加体育锻炼的时间不少于60分钟的频率为
所以周末参加体育锻炼的时间不少于60分钟的人数人.
故选:C
7.A
【分析】
根据定义,结合各组的情况,举出特例排除错误选项;对正确选项,计算即可做出判断.
【详解】
对于甲同学,平均数为,方差小于,设甲同学三次考试的名次分别为、、,
若、、中至少有一个大于等于,则方差为,与已知条件矛盾,
所以,、、均不大于,满足题意;
对于乙同学,平均数为,众数为,则三次考试的成绩的名次为、、,
即必有一次考试为第名,不满足题意;
对于丙同学,中位数为,众数为,可举反例:、、,不满足题意;
对于丁同学,众数为,方差大于,可举特例:、、,则平均数为,
方差为,不满足条件.
故选:A.
【点睛】
关键点点睛:解决本题的关键在于以下两点:
(1)在判断选项不成立时,可通过举反例来否定;
(2)在判断A选项时,可、、中至少有一个大于或等于,利用反证法来推导.
8.C
【分析】
从图中直接观察可以判定AD正确,结合平均数的定义,将比4班多的里面取出部分补到比4班少的班中,可以使得4班的植树量最少,从而判定B正确;结合中位数的定义可以判定C错误.
【详解】
从图可知,2班的植树量少于1班,8班的植树量少于7班,故A正确;
4班的指数棵数为10,11个班中只有2、3、8班三个的植树棵数少于10,且大于5棵,其余7个班的植树棵数都超过10棵,且有6、7、9、10、11班五个班的植树棵数都不少于15棵,将这五个班中的植树棵数各取出5棵,加到2、3、8班中取,除4班外,其余各班的植树棵数都超过了4班,所以4班植树的棵数低于11个班的平均值,故B正确;
比6班植树多的只有9、10、11三个班,其余七个班都比6班少,故6班所对应的植树棵数不是中位数,故C是错误的;
1到5班的植树棵数的极差在10以内,6到11班的植树棵数的极差超过了15,另外从图明显看出,1至5班植树的棵数相对于6至11班,波动更小,变化比较平稳,故D正确;
综上,不正确的只有C,
故选:C.
【点睛】
本题考查频数折线图的意义,涉及平均数,中位数,波动大小的判定,难点是平均数的估算,这里采用取长补短法进行估算,可以避免数字的计算.
9.ABC
【分析】
根据空气质量指数()的月折线图逐一判断即可.
【详解】
每月的平均指数都不超过,故全年的平均指数也不超过,对应的空气质量为优或良,故选项A正确;每月的指数最小值均不超过,故每月都至少有一天空气质量为优,选项B正确;2月,8月,9月和12月的指数最大值均大于,故至少有一天出现了污染天气,故选项C正确;2月,8月,9月,12月中空气质量为“污染”的天数不确定,故选项D不一定正确,
故选:ABC
10.BCD
【分析】
由频率直方图中的数据,根据频率之和为1直接求第七组的频率,由中位数、平均数、方差的求法,判断判断各项的正误.
【详解】
A:设第七组的频率为,则,得,错误;
B:由知:中位数在区间,若中位数为,则:,解得,正确;
C:由图知:,正确;
D:,正确;
故选:BCD.
11.ABC
【分析】
根据中位数、平均数,方差判断三地数据中最低的温度是否低于22℃,即可得.
【详解】
甲地:设甲地的其他两个数据分别为,,且,将5个数据由小到大排列得22,22,24,,,其中,满足进入夏季的标志;
乙地:设乙地其他四个数据分别为,,,,且,将5个数据由小到大排列得,,27,,,则,而,故,其中必有一个小于22,故不满足进入夏季的标志;
丙地:设5个数据分别为,,,,32,且,由方差公式可知,则
,易知,,,均大于22,满足进入夏季的标志综上,ABC正确,
故选:ABC.
12.AB
【分析】
借助于雷达图分析数据,对A、B、C、D一一验证即可.
【详解】
由雷达图易知刀片电池的安全性更高,价格优势更突出,A正确;
三元锂电池的循环寿命较短、价格偏高、安全性偏低,B正确;
对于这7项指标,刀片电池的平均得分为,三元锂电池的平均得分为,所以C错误;
磷酸铁锂电池能量密度低、低温性能差,D错误.
故选:AB
13.200
【分析】
根据频率公式求解.
【详解】
∵,
∴,
故答案为:200
14.13
【分析】
先根据弟弟的销售量的平均数为34,求得y,进而得到其众数,然后再根据哥哥的销售量的中位数比弟弟的销售量的众数大2,得到哥哥的销售量的中位数求解.
【详解】
因为弟弟的销售量的平均数为34,
所以,
解得,
由茎叶图知:弟弟的销售量的众数是34,
因为哥哥的销售量的中位数比弟弟的销售量的众数大2,
所以哥哥的销售量的中位数是36,
所以,解得,
所以,
故答案为:13
15.
【分析】
先分别求出这3组的人数,再利用分层抽样的方法即可得出答案.
【详解】
第3组的人数为,
第4组的人数为,
第5组的人数为,
所以这三组共有60名志愿者,
所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,第三组应抽取名,
故答案为:3.
【点睛】
关键点点睛:该题考查的是有关频率分布直方图的识别以及分层抽样某层抽取个数的问题,正确解题的关键是掌握在抽取过程中每个个题被抽到的机会均等.
16.②③④
【分析】
①由学生类别阅读量图表可知;
②计算75%分位数的位置,在区间内查人数即可;
③设在区间内的初中生人数为,则,分别计算为最大值和最小值时的中位数位置即可;
④设在区间内的初中生人数为,则,分别计算为最大值和最小值时的25%分位数位置即可.
【详解】
在①中,由学生类别阅读量中男生和女生人均阅读量知,这200名学生的平均阅读量在区间内,故错误;
在②中,,阅读量在的人数有人,
在的人数有62人,所以这200名学生阅读量的75%分位数在区间内,
故正确;
在③中,设在区间内的初中生人数为,则,
当时,初中生总人数为116人,,
此时区间有25人,区间有36人,所以中位数在内,
当时,初中生总人数为131人,,
区间有人,区间有36人,所以中位数在内,
当区间人数去最小和最大,中位数都在内,
所以这名学生中的初中生阅读量的中位数一定在区间内,故正确;
在④中,设在区间内的初中生人数为,则,
当时,初中生总人数为116人,,
此时区间有25人,区间有36人,所以25%分位数在内,
当时,初中生总人数为131人,,
区间有人,所以25%分位数在内,
所以这名学生中的初中生阅读量的25%分位数可能在区间内,故正确;
故答案为:②③④
【点睛】
本题主要考查频数分布表、平均数和分位数的计算,考查学生对参数的讨论以及计算能力,属于中档题.
17.(1)10.1分;(2)10.3.
【分析】
(1)由频率直方图,根据平均数计算方法可得答案;
(2)根据中位数的计算方法可得答案.
【详解】
解:(1)由题意,得
中间值 5 7 9 11 13 15
频率 0.1 0.15 0.2 0.3 0.15 0.1
所以
所以这些选手的平均成绩为10.1分.
(2)设这些选手的成绩的中位数为y,
因为,
所以.
所以,则,
故这些选手的成绩的中位数为10.3.
【点睛】
本题考查根据频率直方图求得平均数和中位数,属于基础题.
18.(1)0;(2)乙同学比较合适.
【分析】
(1)由乙的中位数为91,甲的中位数(90+x)小于91得解;
(2)计算甲乙二人三次成绩的平均数、方差等特征数据,再分析选择.
【详解】
(1)由茎叶图可知,乙同学成绩的中位数为.
又由茎叶图可得甲同学成绩的中位数大于或等于,
且甲成绩的中位数小于乙成绩的中位数,所以甲同学成绩的中位数只能为,
故.
(2)甲同学成绩的平均数为,
乙同学成绩的平均数为,
所以甲、乙成绩的平均数相等.
甲同学成绩的方差,
乙同学成绩的方差,
,所以乙同学的成绩更稳定,选乙同学比较合适.
19.(1),p=0.4,q=0.25,直方图见解析;(2)2.13(千元).
【分析】
(1)根据已知条件列出关于的方程组,解之可得,然后由频率公式计算出,补全直方图;
(2)求出网购金额低于2千元的频率为0.2,网购金额低于3千元的频率为0.6,得出网购金额的25百分位数在[2,3)内,利用比例可得.
【详解】
解 (1)根据题意有
解得
所以p=0.4,q=0.25.
补全频率直方图如图所示.
(2)由(1)可知,网购金额低于2千元的频率为0.08+0.12=0.2,
网购金额低于3千元的频率为0.2+0.4=0.6,
所以网购金额的25百分位数在[2,3)内,
则网购金额的25百分位数估计为2+×1=2+0.125≈2.13(千元).
20.(1)、、、、;(2),;(3).
【分析】
(1)由学生编号为、、、…,从第行第列的数开始右读,有943、949、、、、、、、、、、、…,根据编号规则确认符合要求的前5个数字即为所得.
(2)根据表格数据,有,即可求m、n;
(3)由题设知:且,,列举法写出所有可能组合情况,以及数学成绩优比良的人数少的组合情况,求概率.
【详解】
(1)根据图表数据,结合编号规则知:最先抽出的人的编号依次为、、、、;
(2)由,得,
∵,
∴;
(3),且,,
∴满足条件的有:、、、、、、、
、、、、、、共有种,且每组出现都是等可能的,
记:“数学成绩优秀的人数比良的人数少”为事件,事件包括:、、、、、共个基本事件,
∴.
21.(1) (2)67.1 (3)75
【分析】
(1)先求出成绩在30到70的频率为0.6,然后根据条件列出方程求解即可.
(2)先求出成绩在各段的频率,由求平均数的公式可得答案.
(3)先求出录取的频率为0.3,从由右到左求出频率为0.3的点即可.
【详解】
(1)笔试成绩在30到70的频率为
由左边四个小长方形的高度自左向右依次构成公比为2的等比数列,分别设为
所以,解得
所以
(2)成绩在各段的频率分布为:
平均值为:
(3)由于报名者共2000人,计划招收600名新员工,则
由成绩在80到100的频率为.
由于成绩在70到80之间的频率为0.2
所以被录取的分数在70到80之间的频率应为0.1,故录取成绩分数为75.
22.(1)4000;(2)平均收入的估计值为3(千万元);逃税的企业数量为600;(3)至少定为3.
【分析】
(1)先根据表格计算收入大于等于4千万元的频率,再计算企业数量;(2)首先计算平均收入的估计值,再计算平均缴税额,再根据实际缴税总额,计算缴税企业的数量,即可得逃税的企业数量;(3)首先求企业逃税的获利收益的分布列,再求期望,令期望小于0,即可求得的最小值.
【详解】
(1)去年收入大于等于4千万元的频率为,
所以估计该地区去年收入大于等于4千万元的企业数量为.
(2)该地区企业去年的平均收入的估计值为
(千万元).
平均缴税额为(千万元)(亿元),
所以未逃税的企业数量为,
因此,逃税的企业数量为.
(3)设企业应缴税额为,企业逃税的获益为,
若该企业逃税未被查出,则;
若该企业逃税被查出来,则.
由条件知,,
所以,
要对逃税行为起到惩罚作用,则需,解得.
所以至少定为3,才能对逃税行为起到惩罚作用.
【点睛】
关键点点睛:本题考查离散型变量的分布列和数学期望,以及解决实际问题,本题的关键是理解题意,并能转化为数学问题.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
