2020-2021学年华东师大版七年级下册10.1.2 轴对称的再认识课件(共22张)
文档属性
| 名称 | 2020-2021学年华东师大版七年级下册10.1.2 轴对称的再认识课件(共22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 903.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-17 11:12:29 | ||
图片预览






文档简介
10.1 轴对称
第2课时 轴对称的再
认识
第10章 轴对称、平移与旋转
复习引入
什么是轴对称图形?什么是成轴对称图形?它们有什么共同的特征?
如图,为了固定标杆AB,由它上边的某点C向地面上的D、E两点拉两条绳子,使得D、B、E在一条直线上,如果DB=BE,绳子CD和CE有什么关系呢?
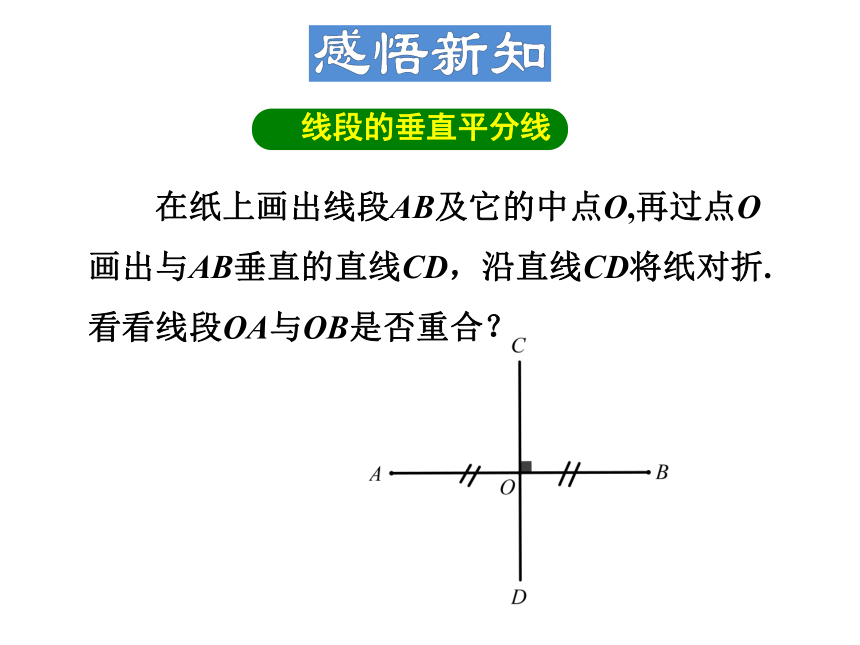
线段的垂直平分线
在纸上画出线段AB及它的中点O,再过点O画出与AB垂直的直线CD,沿直线CD将纸对折.看看线段OA与OB是否重合?
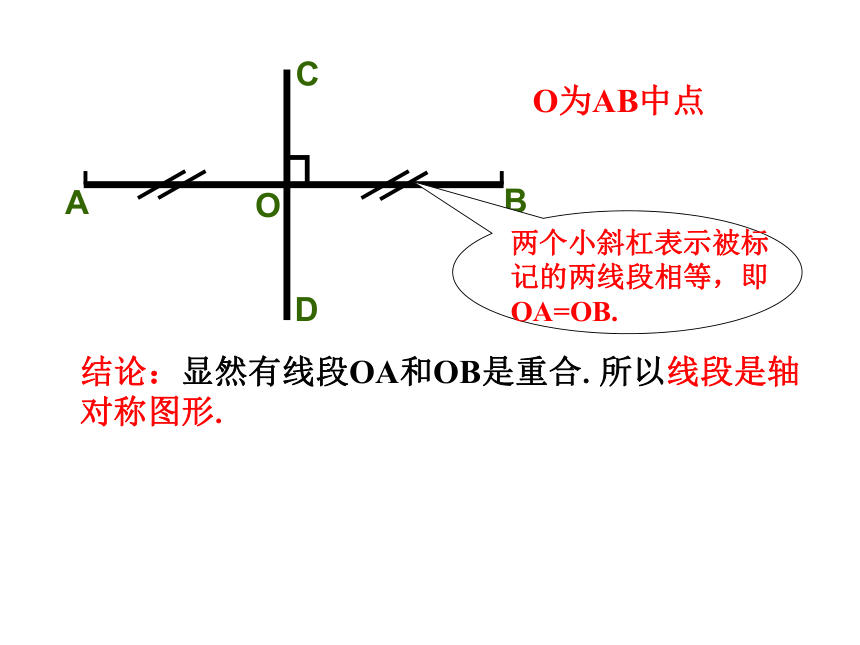
结论:显然有线段OA和OB是重合.所以线段是轴对称图形.
A
B
O
C
D
O为AB中点
两个小斜杠表示被标记的两线段相等,即OA=OB.
线段的垂直平分线(中垂线):
1. 定义:垂直并且平分一条线段的直线叫做这条线段的垂直平分线(中垂线).
要点精析:线段的垂直平分线必须满足两个条件:①经过线段的中点; ②垂直于这条线段.
2. 如图,直线CD是线段AB的
垂直平分线?
如图,直线AE是线段BC的垂直平分线,垂足为E.试说明:∠ABD=∠ACD.
例1
解:
∵AE是线段BC的垂直平分线,点A,D在AE上,
又∵B,C为关于AE对称的两点,
∴△ABD与△ACD关于AE对称,
∴∠ABD=∠ACD.
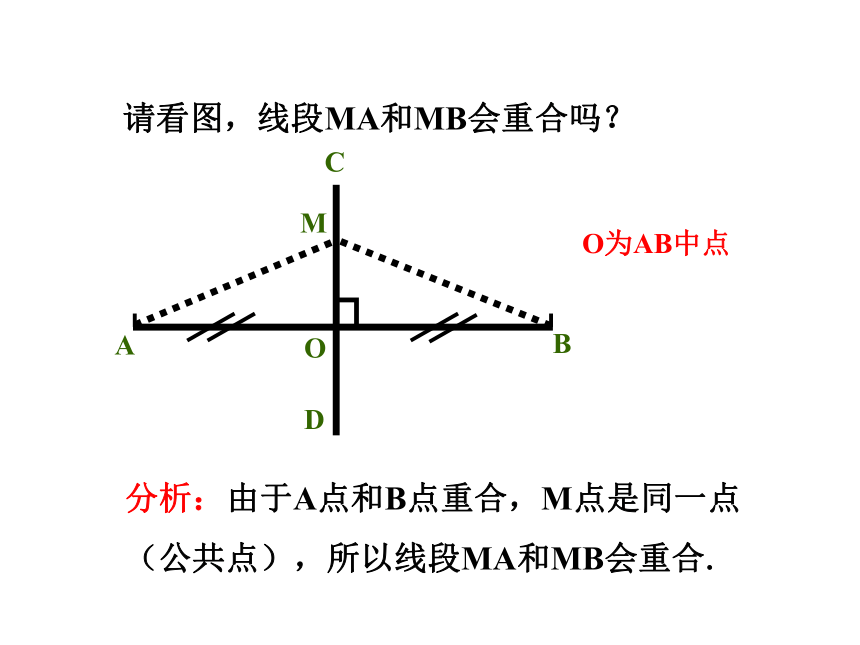
请看图,线段MA和MB会重合吗?
A
B
O
C
D
O为AB中点
M
分析:由于A点和B点重合,M点是同一点(公共点),所以线段MA和MB会重合.
线段垂直平分线的性质:线段的垂直平分线上的点到这条线段两个端点的距离相等。
总结归纳
例2 △ABC中,BC=10,边
BC的垂直平分线分别交AB、
BC于点E、D;BE=6,
求△BCE的周长。
解:∵ED是BC的垂直平分线(已知)
∴EC=EB=6
(线段的垂直平分线上的点到这条线段两个端点的距离相等)
∴△BCE的周长=BC+CE+EB=10+6+6=22
答:△BCE的周长为22。
线段和角的对称性
如图,在半透明纸上画出∠AOB,对折,使角的
两条边完全重合,然后用直尺画出折痕OM,看看射
线OM与∠AOB是什么关系.
A
B
O
P
从上面的操作可以看出,角也是轴对称图形,对称轴是它的角平分线所在的直线.
在研究轴对称图形时,往往需要找到它的对称轴,看看沿对称轴翻折后各部分的对称情况.
角的对称轴是( )
A.角平分线 B. 一条直线
C.角平分线所在的直线 D.不确定
例3
B
对称轴的确定
如图,方格纸内的两图形都是轴对称图形,请画
出它们的对称轴.
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
画出下列图形的对称轴.
如果没有方格子,而又不能折叠,你还能比较准确的画出图形的对称轴吗?
问题1.试着分别画出下图所示图形的对称轴.
用折叠的方法可以检验自己画的对称轴是否准确.如果不能折叠,又该如何判断对称轴的位置呢?
连结对称点的线段被对称轴垂直平分
问题2:如图1,点A和点A′关于某条直线成轴对称,你能画出这条直线吗?
A . . A’
我们只要连结点A和点A′ ,取线段AA′的中点O,过点O画直线l,使l垂直于A A′ ,即画出线段AA′的垂直平分线l,直线l 就是点A和点A′的对称轴.
我们现在可以总结出其他复杂的轴对称图形的对
称轴的画法:
①先找出轴对称图形的任意一组对称点,
②连结对称点,得到一条线段,
③画出这条线段的垂直平分线,
就可以得到该图形的对称轴.
1. 如果一个图形是轴对称图形,那么连结对称点的线
段的垂直平分线就是该图形的对称轴.
2. 已知一个轴对称图形或已知两个图形成轴对称,画
出其对称轴的方法:
方法一:折叠法:将一个轴对称图形(或两个成轴对
称的图形)沿图形间的某条直线对折,使这个图形的
两部分(或两个图形)能完全重合,这条折痕所在的
直线就是这个轴对称图形(或两个成轴对称的图形)
的对称轴.
方法二:作垂直平分线:
(1)找出轴对称图形(或两个成轴对称的图形)的任意一
组对称点;
(2)连结这组对称点,得一条线段;
(3)画出这条线段的垂直平分线,则这条线段的垂直平
分线就是该图形(或这两个图形)的对称轴.此画法
可简记为“一找二连三画垂直平分线”.
画出下图中各图形的一条对称轴.
例4
解:
如图,直线l即为对称轴.
确定轴对称图形的对称轴:
①找任意一组对称点;
②连结对称点,得到一条线段;
③作这条线段的垂直平分线,就可以得到该图形
的对称轴,简称:一找点二连线三画中垂线.
第2课时 轴对称的再
认识
第10章 轴对称、平移与旋转
复习引入
什么是轴对称图形?什么是成轴对称图形?它们有什么共同的特征?
如图,为了固定标杆AB,由它上边的某点C向地面上的D、E两点拉两条绳子,使得D、B、E在一条直线上,如果DB=BE,绳子CD和CE有什么关系呢?
线段的垂直平分线
在纸上画出线段AB及它的中点O,再过点O画出与AB垂直的直线CD,沿直线CD将纸对折.看看线段OA与OB是否重合?
结论:显然有线段OA和OB是重合.所以线段是轴对称图形.
A
B
O
C
D
O为AB中点
两个小斜杠表示被标记的两线段相等,即OA=OB.
线段的垂直平分线(中垂线):
1. 定义:垂直并且平分一条线段的直线叫做这条线段的垂直平分线(中垂线).
要点精析:线段的垂直平分线必须满足两个条件:①经过线段的中点; ②垂直于这条线段.
2. 如图,直线CD是线段AB的
垂直平分线?
如图,直线AE是线段BC的垂直平分线,垂足为E.试说明:∠ABD=∠ACD.
例1
解:
∵AE是线段BC的垂直平分线,点A,D在AE上,
又∵B,C为关于AE对称的两点,
∴△ABD与△ACD关于AE对称,
∴∠ABD=∠ACD.
请看图,线段MA和MB会重合吗?
A
B
O
C
D
O为AB中点
M
分析:由于A点和B点重合,M点是同一点(公共点),所以线段MA和MB会重合.
线段垂直平分线的性质:线段的垂直平分线上的点到这条线段两个端点的距离相等。
总结归纳
例2 △ABC中,BC=10,边
BC的垂直平分线分别交AB、
BC于点E、D;BE=6,
求△BCE的周长。
解:∵ED是BC的垂直平分线(已知)
∴EC=EB=6
(线段的垂直平分线上的点到这条线段两个端点的距离相等)
∴△BCE的周长=BC+CE+EB=10+6+6=22
答:△BCE的周长为22。
线段和角的对称性
如图,在半透明纸上画出∠AOB,对折,使角的
两条边完全重合,然后用直尺画出折痕OM,看看射
线OM与∠AOB是什么关系.
A
B
O
P
从上面的操作可以看出,角也是轴对称图形,对称轴是它的角平分线所在的直线.
在研究轴对称图形时,往往需要找到它的对称轴,看看沿对称轴翻折后各部分的对称情况.
角的对称轴是( )
A.角平分线 B. 一条直线
C.角平分线所在的直线 D.不确定
例3
B
对称轴的确定
如图,方格纸内的两图形都是轴对称图形,请画
出它们的对称轴.
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
画出下列图形的对称轴.
如果没有方格子,而又不能折叠,你还能比较准确的画出图形的对称轴吗?
问题1.试着分别画出下图所示图形的对称轴.
用折叠的方法可以检验自己画的对称轴是否准确.如果不能折叠,又该如何判断对称轴的位置呢?
连结对称点的线段被对称轴垂直平分
问题2:如图1,点A和点A′关于某条直线成轴对称,你能画出这条直线吗?
A . . A’
我们只要连结点A和点A′ ,取线段AA′的中点O,过点O画直线l,使l垂直于A A′ ,即画出线段AA′的垂直平分线l,直线l 就是点A和点A′的对称轴.
我们现在可以总结出其他复杂的轴对称图形的对
称轴的画法:
①先找出轴对称图形的任意一组对称点,
②连结对称点,得到一条线段,
③画出这条线段的垂直平分线,
就可以得到该图形的对称轴.
1. 如果一个图形是轴对称图形,那么连结对称点的线
段的垂直平分线就是该图形的对称轴.
2. 已知一个轴对称图形或已知两个图形成轴对称,画
出其对称轴的方法:
方法一:折叠法:将一个轴对称图形(或两个成轴对
称的图形)沿图形间的某条直线对折,使这个图形的
两部分(或两个图形)能完全重合,这条折痕所在的
直线就是这个轴对称图形(或两个成轴对称的图形)
的对称轴.
方法二:作垂直平分线:
(1)找出轴对称图形(或两个成轴对称的图形)的任意一
组对称点;
(2)连结这组对称点,得一条线段;
(3)画出这条线段的垂直平分线,则这条线段的垂直平
分线就是该图形(或这两个图形)的对称轴.此画法
可简记为“一找二连三画垂直平分线”.
画出下图中各图形的一条对称轴.
例4
解:
如图,直线l即为对称轴.
确定轴对称图形的对称轴:
①找任意一组对称点;
②连结对称点,得到一条线段;
③作这条线段的垂直平分线,就可以得到该图形
的对称轴,简称:一找点二连线三画中垂线.
