2020-2021学年华东师大版七年级下册10.3.3 旋转对称图形课件(共15张)
文档属性
| 名称 | 2020-2021学年华东师大版七年级下册10.3.3 旋转对称图形课件(共15张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 275.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-17 11:14:55 | ||
图片预览






文档简介
10.3 旋转
第3课时 旋转对称图形
第10章 轴对称、平移与旋转
旋转的特征有哪些?
2.对应线段相等,对应角相等
3.图形上的每一点都绕旋转中心沿相同的方向转动了相同
大小的角度。
1.图形旋转前后形状,大小不变
4.对应点到旋转中心的距离相等。
复习
怎样画一个图形关于一个点旋转后的图形?
如何来确定旋转中心?
主要是画几个点旋转后的点
用两组对应点连线的中垂线的交点
思考:
试一试:用一张半透明的薄纸,覆盖在如下所示的图形上,在薄纸上画这个图形,使它与下图完全重合.然后固定圆心,将薄纸旋转,猜想旋转多少度(小于周角)后,薄纸上的图形能与原图再一次重合?
A
C
D
E
F
O
60°,120°,180°,240°,300°
该图形绕哪一点旋转?
O点
注意:若顺时针或逆时针旋转一定角度,该图形都能与原图形重合,则可以淡化旋转方向.
旋转对称图形
1. 定义:如果一个图形绕着某一定点旋转一定角度后
能与自身重合,那么这个图形就叫做旋转对称图形.
2. 旋转对称图形的旋转角度:
(1)旋转角的范围:大于0°且小于360°;
(2)最小旋转角度:最小旋转角度= ;
(3)旋转角度:旋转角度是最小旋转角度的整数倍.
为了提高学生们的设计能力,某中学举办了图案设计大赛,如图所示的是四名参赛选手设计的图案.其中是旋转对称图形的是( )
例1
D
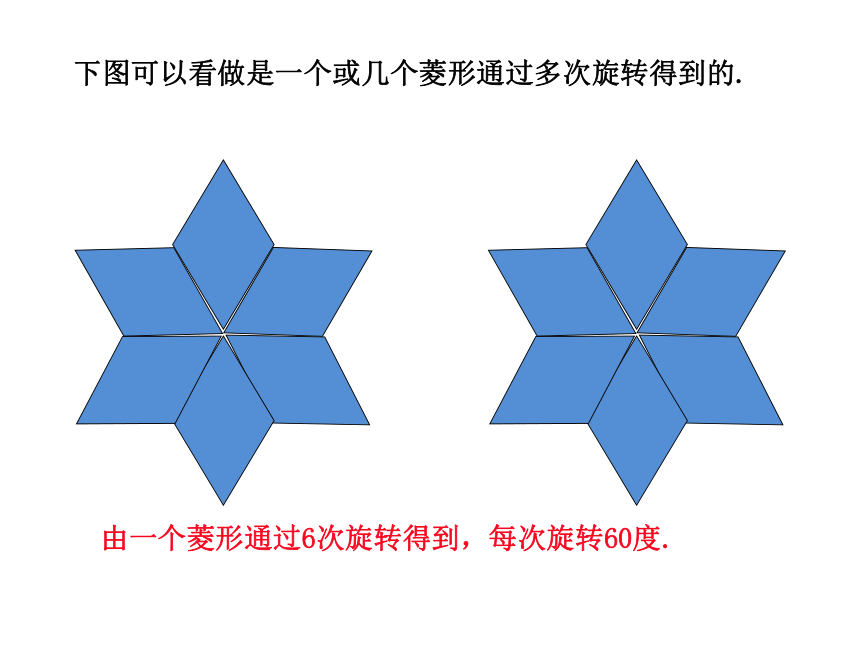
下图可以看做是一个或几个菱形通过多次旋转得到的.
由一个菱形通过6次旋转得到,每次旋转60度.
由两个菱形旋转3次得到,每次旋转120度.
由三个菱形旋转2次得到,旋转180度.
旋转对称图形的形成
用类似上述的操作方法对如图所示的图形进行探
索,看看它是不是旋转对称
图形.若是,想一想旋转中心
在何处,需要旋转多少度后,
能与自身重合.该图形还是轴
对称图形吗?
例2. 下列各图形是不是旋转对称图形?如果是,请找出旋转中心在何处.旋转角度是多少?这些图形是轴对称图形吗?
如图所示的图形各绕哪一点至少需要旋转多少度后,能与它自身重合?
例3
解:
①绕圆心至少需要旋转180°后,能与它自身重合.
②绕中心至少需要旋转120°后,能与它自身重合.
③绕圆心至少需要旋转60°后,能与它自身重合.
④绕正方形的中心至少需要旋转90°后,能与它自
身重合.
如图,△ABC中,∠BAC=90°,P是△ABC内一点,将△ABP绕点A逆时针旋转一定角度后能与△ACQ重合,如果AP=3,那么△APQ的面积是多少?
例4
解:
因为将△ABP绕点A逆时针旋转一定角度后能与
△ACQ重合,
所以AP=AQ=3,AB=AC.
因为∠BAC=90°,所以∠PAQ=90°,
所以△PAQ是等腰直角三角形.
所以S△APQ=
当堂练习
B
A
3、请大家欣赏下列图形,它们是旋转对称图形吗?它们还是轴对称图形吗?如果是旋转图形想一想它们的旋转中心在哪里?旋转角度是多少?
三个图形都是旋转对称图形,也都是轴对称图形;
它们的旋转中心为对称轴的交点;
最小旋转角分别为60°,72°,90°.
1. 一个旋转对称图形旋转的角度可能不止一种.
2. 旋转对称图形的旋转中心一定在图形内或图形上.
3. 旋转角不确定时,先在0°~360°范围内找出其旋
转后能与自身重合的最小角度,并在此范围内找出
所有这一最小角度的倍数,那么这一图形旋转这一
最小角度的整数倍数后均与原图形重合.
第3课时 旋转对称图形
第10章 轴对称、平移与旋转
旋转的特征有哪些?
2.对应线段相等,对应角相等
3.图形上的每一点都绕旋转中心沿相同的方向转动了相同
大小的角度。
1.图形旋转前后形状,大小不变
4.对应点到旋转中心的距离相等。
复习
怎样画一个图形关于一个点旋转后的图形?
如何来确定旋转中心?
主要是画几个点旋转后的点
用两组对应点连线的中垂线的交点
思考:
试一试:用一张半透明的薄纸,覆盖在如下所示的图形上,在薄纸上画这个图形,使它与下图完全重合.然后固定圆心,将薄纸旋转,猜想旋转多少度(小于周角)后,薄纸上的图形能与原图再一次重合?
A
C
D
E
F
O
60°,120°,180°,240°,300°
该图形绕哪一点旋转?
O点
注意:若顺时针或逆时针旋转一定角度,该图形都能与原图形重合,则可以淡化旋转方向.
旋转对称图形
1. 定义:如果一个图形绕着某一定点旋转一定角度后
能与自身重合,那么这个图形就叫做旋转对称图形.
2. 旋转对称图形的旋转角度:
(1)旋转角的范围:大于0°且小于360°;
(2)最小旋转角度:最小旋转角度= ;
(3)旋转角度:旋转角度是最小旋转角度的整数倍.
为了提高学生们的设计能力,某中学举办了图案设计大赛,如图所示的是四名参赛选手设计的图案.其中是旋转对称图形的是( )
例1
D
下图可以看做是一个或几个菱形通过多次旋转得到的.
由一个菱形通过6次旋转得到,每次旋转60度.
由两个菱形旋转3次得到,每次旋转120度.
由三个菱形旋转2次得到,旋转180度.
旋转对称图形的形成
用类似上述的操作方法对如图所示的图形进行探
索,看看它是不是旋转对称
图形.若是,想一想旋转中心
在何处,需要旋转多少度后,
能与自身重合.该图形还是轴
对称图形吗?
例2. 下列各图形是不是旋转对称图形?如果是,请找出旋转中心在何处.旋转角度是多少?这些图形是轴对称图形吗?
如图所示的图形各绕哪一点至少需要旋转多少度后,能与它自身重合?
例3
解:
①绕圆心至少需要旋转180°后,能与它自身重合.
②绕中心至少需要旋转120°后,能与它自身重合.
③绕圆心至少需要旋转60°后,能与它自身重合.
④绕正方形的中心至少需要旋转90°后,能与它自
身重合.
如图,△ABC中,∠BAC=90°,P是△ABC内一点,将△ABP绕点A逆时针旋转一定角度后能与△ACQ重合,如果AP=3,那么△APQ的面积是多少?
例4
解:
因为将△ABP绕点A逆时针旋转一定角度后能与
△ACQ重合,
所以AP=AQ=3,AB=AC.
因为∠BAC=90°,所以∠PAQ=90°,
所以△PAQ是等腰直角三角形.
所以S△APQ=
当堂练习
B
A
3、请大家欣赏下列图形,它们是旋转对称图形吗?它们还是轴对称图形吗?如果是旋转图形想一想它们的旋转中心在哪里?旋转角度是多少?
三个图形都是旋转对称图形,也都是轴对称图形;
它们的旋转中心为对称轴的交点;
最小旋转角分别为60°,72°,90°.
1. 一个旋转对称图形旋转的角度可能不止一种.
2. 旋转对称图形的旋转中心一定在图形内或图形上.
3. 旋转角不确定时,先在0°~360°范围内找出其旋
转后能与自身重合的最小角度,并在此范围内找出
所有这一最小角度的倍数,那么这一图形旋转这一
最小角度的整数倍数后均与原图形重合.
