2020--2021学年人教版七年级数学下册同步课件:8.3 第2课时 几何图形、经济生活和行程问题(共15张ppt)
文档属性
| 名称 | 2020--2021学年人教版七年级数学下册同步课件:8.3 第2课时 几何图形、经济生活和行程问题(共15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 196.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-17 10:33:00 | ||
图片预览



文档简介
第八章 二元一次方程组
8.3 第2课时
几何图形、经济生活与行程问题
获取新知
探 究
知识点一:几何图形问题
据统计资料,甲、乙两种作物的单位面积产量的比是1:2.现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
问题:把长方形分割成两个长方形有哪些分割方法?
(1)竖着分割,把长分成两段,宽不变;
(2)横着分割,把宽分成两段,长不变.
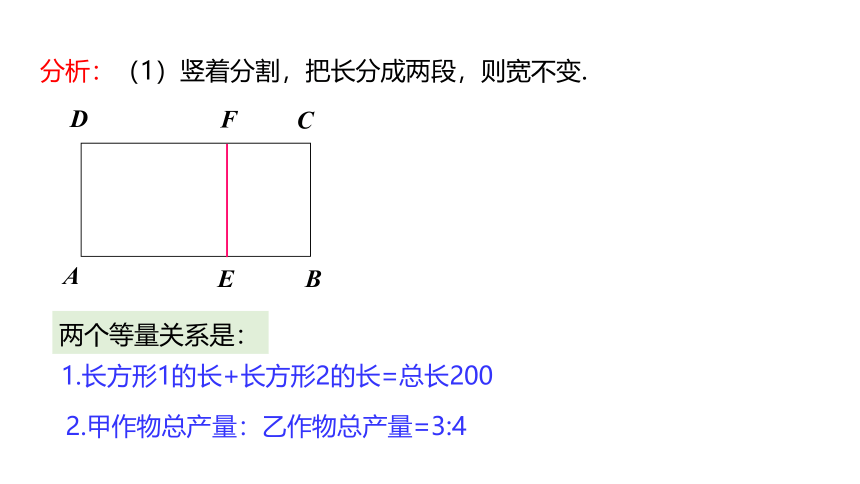
分析:(1)竖着分割,把长分成两段,则宽不变.
A
D
C
F
B
E
1.长方形1的长+长方形2的长=总长200
2.甲作物总产量:乙作物总产量=3:4
两个等量关系是:
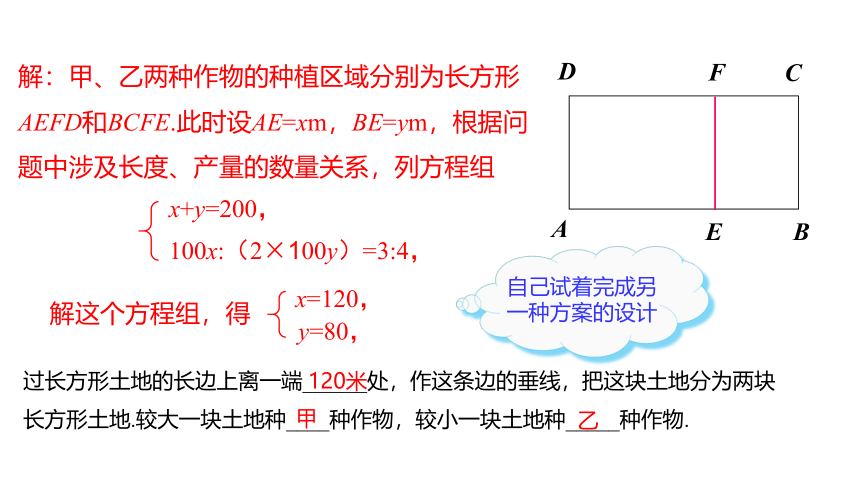
解:甲、乙两种作物的种植区域分别为长方形AEFD和BCFE.此时设AE=xm,BE=ym,根据问题中涉及长度、产量的数量关系,列方程组
A
D
C
F
B
E
100x:(2×100y)=3:4,
x+y=200,
解这个方程组,得
x=120,
y=80,
过长方形土地的长边上离一端______处,作这条边的垂线,把这块土地分为两块
长方形土地.较大一块土地种____种作物,较小一块土地种_____种作物.
120米
甲
乙
自己试着完成另一种方案的设计
获取新知
知识点二:经济生活问题
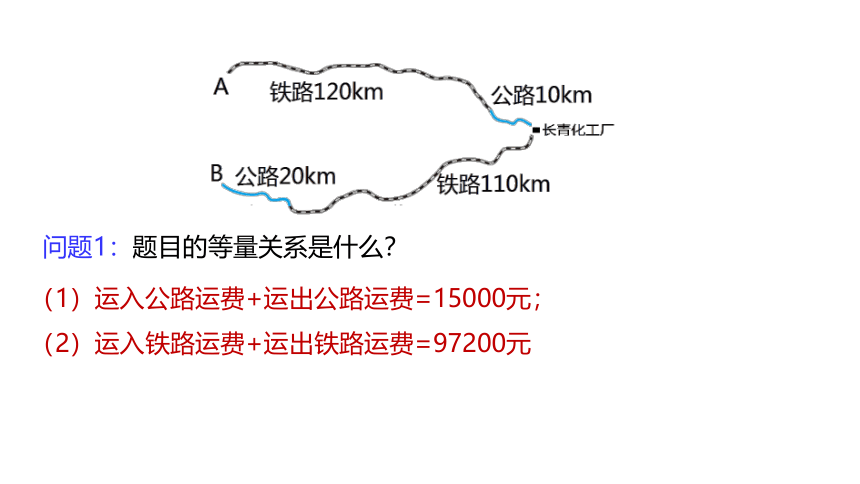
如图,长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5 元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元,这批产品的销售款比原料费与运输费的和多多少元?
探 究
问题1:题目的等量关系是什么?
(1)运入公路运费+运出公路运费=15000元;
(2)运入铁路运费+运出铁路运费=97200元
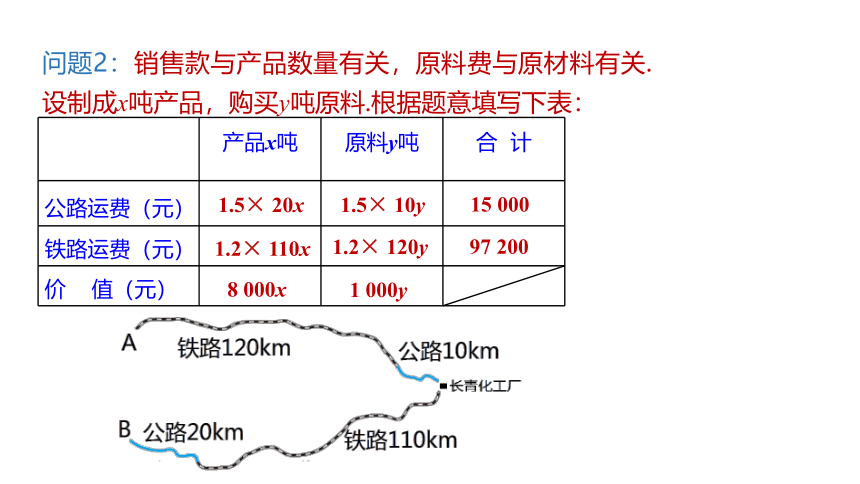
问题2:销售款与产品数量有关,原料费与原材料有关.设制成x吨产品,购买y吨原料.根据题意填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
产品x吨
原料y吨
合 计
公路运费(元)
铁路运费(元)
价 值(元)
1.5× 20x
1.2× 110x
8 000x
1.5× 10y
1.2× 120y
1 000y
15 000
97 200
解:根据图表,列出方程组
解方程组得
x=300,
y=400.
8000x-1000y-15 000-97 200
=8000×300-1 000×400-15 000-97 200
=1 887 800(元).
这批产品的销售款比原料费与运输费的和多1887800元.
1.5 × 20x+ 1.5×10y=15000,
1.2 × 110x+ 1.2×120y=97200.
获取新知
知识点三:行程问题
甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
分析:对于行程问题,一般可以借助示意图表示题中的数量关系,可以更加直观的找到相等关系.
(1) 同时出发,同向而行
甲2h行程=4km+乙2h行程
(2) 同时出发,相向而行
甲0.5h行程+乙0.5h行程=4km
甲出发点
乙出发点
4km
甲追上乙
乙2h行程
甲2h行程
甲出发点
乙出发点
4km
相遇地
甲0.5h
行程
乙0.5h
行程
解:设甲、乙的速度分别为xkm/h,ykm/h.
根据题意,得
解方程组,得
答:甲的速度为5km/h,乙的速度为3km/h.
随堂演练
1.一个长方形,它的长减少4cm,宽增加2cm,所得的是一个正方形,它的面积与长方形的面积相等,求原长方形的长与宽.
解:设长方形的长为xcm,宽为ycm,由题意得:
解方程组,得
答:原长方形的长与宽分别为8cm和2cm.
2.某班有40名同学看演出,购买甲、乙两种票共用去370元,其中甲种票每张10元,乙种票每张8元.请问甲种和乙种票各多少张?
答:甲种票25张,乙种票15张.
解:设甲种票为x张,乙种票为y张,由题意得:
解方程组,得
3.某船顺流航行36km用3h,逆流航行24km用3 h,则水流速度和船在静水中的速度各是多少?
答:船在静水中的速度为10km/h,水流速度为2km/h.
解:设船在静水中的速度为xkm/h,水流的速度为ykm/h,根据题意,得:
解方程组,得
课堂小结
二元一次方程组的应用
应用
步骤
几何图形问题
审题:弄清题意和题目中的数量关系
设元:用字母表示题目中的未知数
列方程组:根据两个等量关系列出方程组
解方程组
检验作答
行程问题
经济生活问题
8.3 第2课时
几何图形、经济生活与行程问题
获取新知
探 究
知识点一:几何图形问题
据统计资料,甲、乙两种作物的单位面积产量的比是1:2.现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
问题:把长方形分割成两个长方形有哪些分割方法?
(1)竖着分割,把长分成两段,宽不变;
(2)横着分割,把宽分成两段,长不变.
分析:(1)竖着分割,把长分成两段,则宽不变.
A
D
C
F
B
E
1.长方形1的长+长方形2的长=总长200
2.甲作物总产量:乙作物总产量=3:4
两个等量关系是:
解:甲、乙两种作物的种植区域分别为长方形AEFD和BCFE.此时设AE=xm,BE=ym,根据问题中涉及长度、产量的数量关系,列方程组
A
D
C
F
B
E
100x:(2×100y)=3:4,
x+y=200,
解这个方程组,得
x=120,
y=80,
过长方形土地的长边上离一端______处,作这条边的垂线,把这块土地分为两块
长方形土地.较大一块土地种____种作物,较小一块土地种_____种作物.
120米
甲
乙
自己试着完成另一种方案的设计
获取新知
知识点二:经济生活问题
如图,长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5 元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元,这批产品的销售款比原料费与运输费的和多多少元?
探 究
问题1:题目的等量关系是什么?
(1)运入公路运费+运出公路运费=15000元;
(2)运入铁路运费+运出铁路运费=97200元
问题2:销售款与产品数量有关,原料费与原材料有关.设制成x吨产品,购买y吨原料.根据题意填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
产品x吨
原料y吨
合 计
公路运费(元)
铁路运费(元)
价 值(元)
1.5× 20x
1.2× 110x
8 000x
1.5× 10y
1.2× 120y
1 000y
15 000
97 200
解:根据图表,列出方程组
解方程组得
x=300,
y=400.
8000x-1000y-15 000-97 200
=8000×300-1 000×400-15 000-97 200
=1 887 800(元).
这批产品的销售款比原料费与运输费的和多1887800元.
1.5 × 20x+ 1.5×10y=15000,
1.2 × 110x+ 1.2×120y=97200.
获取新知
知识点三:行程问题
甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
分析:对于行程问题,一般可以借助示意图表示题中的数量关系,可以更加直观的找到相等关系.
(1) 同时出发,同向而行
甲2h行程=4km+乙2h行程
(2) 同时出发,相向而行
甲0.5h行程+乙0.5h行程=4km
甲出发点
乙出发点
4km
甲追上乙
乙2h行程
甲2h行程
甲出发点
乙出发点
4km
相遇地
甲0.5h
行程
乙0.5h
行程
解:设甲、乙的速度分别为xkm/h,ykm/h.
根据题意,得
解方程组,得
答:甲的速度为5km/h,乙的速度为3km/h.
随堂演练
1.一个长方形,它的长减少4cm,宽增加2cm,所得的是一个正方形,它的面积与长方形的面积相等,求原长方形的长与宽.
解:设长方形的长为xcm,宽为ycm,由题意得:
解方程组,得
答:原长方形的长与宽分别为8cm和2cm.
2.某班有40名同学看演出,购买甲、乙两种票共用去370元,其中甲种票每张10元,乙种票每张8元.请问甲种和乙种票各多少张?
答:甲种票25张,乙种票15张.
解:设甲种票为x张,乙种票为y张,由题意得:
解方程组,得
3.某船顺流航行36km用3h,逆流航行24km用3 h,则水流速度和船在静水中的速度各是多少?
答:船在静水中的速度为10km/h,水流速度为2km/h.
解:设船在静水中的速度为xkm/h,水流的速度为ykm/h,根据题意,得:
解方程组,得
课堂小结
二元一次方程组的应用
应用
步骤
几何图形问题
审题:弄清题意和题目中的数量关系
设元:用字母表示题目中的未知数
列方程组:根据两个等量关系列出方程组
解方程组
检验作答
行程问题
经济生活问题
