2020-2021学年七年级数学苏科版下册11.3不等式的基本性质课件(26张ppt)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册11.3不等式的基本性质课件(26张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 857.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-17 13:34:34 | ||
图片预览








文档简介
(共26张PPT)
2021
11.3
不等式的基本性质
苏科版七年级下册
数学
复习引入
1
1.什么叫不等式的解?
2.什么叫不等式的解集?
知识回顾:
能使不等式成立的未知数的值叫不等式的解.
一个含有未知数的不等式的所有的解,组成这个不等式的解的集合,简称为这个不等式的解集
教学新知
2
我是哥哥,今年六岁
我是弟弟,今年四岁
再过3年,我比你大!
你同意弟弟的说话吗?
不对,3年前你比我大
!
你同意哥哥的说话吗?
若不同意,请从不等式的角度分析错的原因.
例如:
因为4
<
6
所以________
.
若不同意请从不等式的角度分析错误原因.
例如:因为4<6
所以————.
设置情境
通过上面的讨论,我们有什么发现?
不等式的性质1:
不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
用数学式子表示:
如果a>b,那么a+
c
>b+
,a-
c
>b-
.
c
c
归纳总结
2.由a<b,要得到a+3<b+3,需要把不等式两边都
,根据是
;
加3
不等式的性质1
3.由2x+3≥-5,根据不等式性质1,左右两边同时
,可化为
2x≥-8
.
1.由-3x-4≤-5,左右两边同时+4,可化为:
,根据______________;
减
3
-3x≤-1
不等式的性质1
当堂练习
5×(-1)
3×(-1),
5×(-2)
3×(-2),
5×(-3)
3×(-3),
5×(-4)
3×(-4),
···
5×(-1)
3×(-1),
5×(-2)
3×(-2),
5×(-3)
3×(-3),
5×(-4)
3×(-4),
···
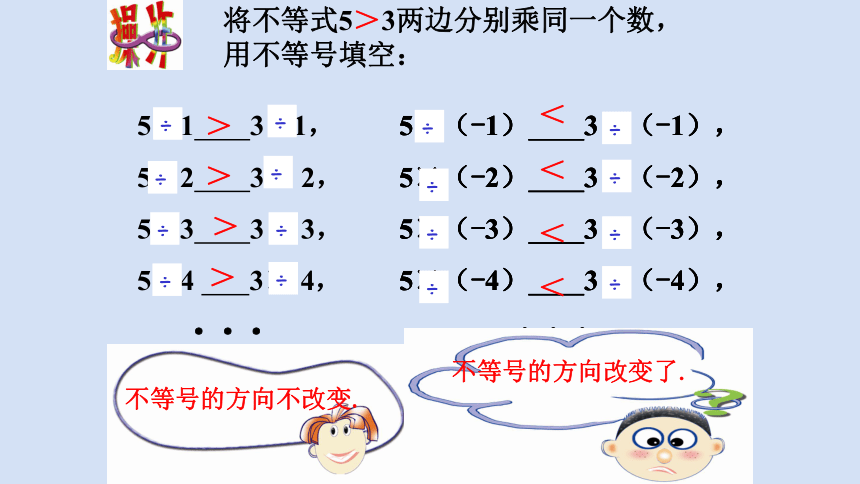
将不等式5>3两边分别乘同一个数,用不等号填空:
5×1
3×1,
5×2
3×
2,
5×3
3×
3,
5×4
3×
4,
···
5×(-1)
3×(-1),
5×(-2)
3×(-2),
5×(-3)
3×(-3),
5×(-4)
3×(-4),
···
不等号的方向不改变.
不等号的方向改变了.
>
>
>
>
<
<
<
<
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
不等式的性质2:
不等式的两边都乘(或除以)同一个
,不等号的方向不变;
不等式的两边都乘(或除以)同一个
,不等号的方向改变.
负数
正数
如果a>b,c>0
,那么ac>bc,
如果a>b,c<0
,那么ac深入思考:
(1)不等式两边同时乘0,不等式的符号会发生怎样的变化?
如:7 4,
而
7×0___
4×0.
验证猜想:不等式的性质和等式的性质相比较有什么
相同点与不同点?
>
=
提示:比较不等式的两个性质与等式的两个性质
若a>b,则
(1)
2a
2b;(理由)
(2)
-4a
-4b;(理由)
(3)
___
.
(理由)
>
<
<
当堂检测
3
>
>
>
<
如果
,那么:
①
②
③
④
(不等式性质
)
(不等式性质
)
(不等式性质
)
(不等式性质
)
1
2
2
1
2、判断正误:
(1)如果a>b,那么ac>bc。
(2)如果a>b,那么ac2>bc2。
(3)如果ac2>bc2,
那么a>b。
×
×
1.已知a>b,用“>”或“<”号填空:
(1)a+2
b+2;
(2)a-5
b-5;
(3)6a
6b;
(4)-a
-b;
(5)2a-3
2b-3;
(6)-4a+3
-4b+3.
2.说出下列不等式变形的依据:
(1)由x-1
>2,得
x>3;
(2)由2x>-4,得
x>-2;
(3)由-0.5x
<-1,得
x
>2;
(4)由3x
<
x,得2x
<
0
.
>
>
>
>
<
<
例1:将下列不等式化成“x>a”或“x<a”的形式:
(1)x-5>-1;
(2)3x<-9;
(3)-2x>3.
例2:将下列不等式化成“x>a”或“x<a”的形式:
(1)3x
<x
-6
(2)7x
>6x
-4;
(3)-2x
<
5x
-6.
将下列不等式化成“x>a”或“x<a”的形式:
(1)x-5>-1;
(2)3x<-9;
(3)-2x>3;
(4
)3x
<x
-6.
【例】
课堂小结
4
你今天这节课有什么收获呢?
我今天学到了
……
11.3 不等式的基本性质
课堂反馈
5
D
A
<
不等式的基本性质1
<
不等式的基本性质2
>
不等式的基本性质2
a>1
2021
11.3
不等式的基本性质
苏科版七年级下册
数学
复习引入
1
1.什么叫不等式的解?
2.什么叫不等式的解集?
知识回顾:
能使不等式成立的未知数的值叫不等式的解.
一个含有未知数的不等式的所有的解,组成这个不等式的解的集合,简称为这个不等式的解集
教学新知
2
我是哥哥,今年六岁
我是弟弟,今年四岁
再过3年,我比你大!
你同意弟弟的说话吗?
不对,3年前你比我大
!
你同意哥哥的说话吗?
若不同意,请从不等式的角度分析错的原因.
例如:
因为4
<
6
所以________
.
若不同意请从不等式的角度分析错误原因.
例如:因为4<6
所以————.
设置情境
通过上面的讨论,我们有什么发现?
不等式的性质1:
不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
用数学式子表示:
如果a>b,那么a+
c
>b+
,a-
c
>b-
.
c
c
归纳总结
2.由a<b,要得到a+3<b+3,需要把不等式两边都
,根据是
;
加3
不等式的性质1
3.由2x+3≥-5,根据不等式性质1,左右两边同时
,可化为
2x≥-8
.
1.由-3x-4≤-5,左右两边同时+4,可化为:
,根据______________;
减
3
-3x≤-1
不等式的性质1
当堂练习
5×(-1)
3×(-1),
5×(-2)
3×(-2),
5×(-3)
3×(-3),
5×(-4)
3×(-4),
···
5×(-1)
3×(-1),
5×(-2)
3×(-2),
5×(-3)
3×(-3),
5×(-4)
3×(-4),
···
将不等式5>3两边分别乘同一个数,用不等号填空:
5×1
3×1,
5×2
3×
2,
5×3
3×
3,
5×4
3×
4,
···
5×(-1)
3×(-1),
5×(-2)
3×(-2),
5×(-3)
3×(-3),
5×(-4)
3×(-4),
···
不等号的方向不改变.
不等号的方向改变了.
>
>
>
>
<
<
<
<
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
不等式的性质2:
不等式的两边都乘(或除以)同一个
,不等号的方向不变;
不等式的两边都乘(或除以)同一个
,不等号的方向改变.
负数
正数
如果a>b,c>0
,那么ac>bc,
如果a>b,c<0
,那么ac
(1)不等式两边同时乘0,不等式的符号会发生怎样的变化?
如:7 4,
而
7×0___
4×0.
验证猜想:不等式的性质和等式的性质相比较有什么
相同点与不同点?
>
=
提示:比较不等式的两个性质与等式的两个性质
若a>b,则
(1)
2a
2b;(理由)
(2)
-4a
-4b;(理由)
(3)
___
.
(理由)
>
<
<
当堂检测
3
>
>
>
<
如果
,那么:
①
②
③
④
(不等式性质
)
(不等式性质
)
(不等式性质
)
(不等式性质
)
1
2
2
1
2、判断正误:
(1)如果a>b,那么ac>bc。
(2)如果a>b,那么ac2>bc2。
(3)如果ac2>bc2,
那么a>b。
×
×
1.已知a>b,用“>”或“<”号填空:
(1)a+2
b+2;
(2)a-5
b-5;
(3)6a
6b;
(4)-a
-b;
(5)2a-3
2b-3;
(6)-4a+3
-4b+3.
2.说出下列不等式变形的依据:
(1)由x-1
>2,得
x>3;
(2)由2x>-4,得
x>-2;
(3)由-0.5x
<-1,得
x
>2;
(4)由3x
<
x,得2x
<
0
.
>
>
>
>
<
<
例1:将下列不等式化成“x>a”或“x<a”的形式:
(1)x-5>-1;
(2)3x<-9;
(3)-2x>3.
例2:将下列不等式化成“x>a”或“x<a”的形式:
(1)3x
<x
-6
(2)7x
>6x
-4;
(3)-2x
<
5x
-6.
将下列不等式化成“x>a”或“x<a”的形式:
(1)x-5>-1;
(2)3x<-9;
(3)-2x>3;
(4
)3x
<x
-6.
【例】
课堂小结
4
你今天这节课有什么收获呢?
我今天学到了
……
11.3 不等式的基本性质
课堂反馈
5
D
A
<
不等式的基本性质1
<
不等式的基本性质2
>
不等式的基本性质2
a>1
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
