2.3抛物线及其标准方程
图片预览


文档简介
2.3 抛物线及其标准方程
例 1 (1)已知抛物线的标准方程是 y2= 6x,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程.
解:(1)因为p=3,所以焦点坐标是(,0),准线方程是x=-.
(2)因为焦点在y轴的负半轴上,并且=2,p=4,所以所求抛物线的标准方程是
x2=-8y.
例2 点M与点F(4,0)的距离比它到直线l:x+5=0的距离小1,求点M的轨迹方程.
分析:由已知,点M属于集合 P={M||MF|+1=|x+5|}.
将|MF|用点的坐标表示出来,化简后就可得到点M的轨迹方程.但这种解法的化简过程比较烦琐.
仔细分析题目的条件,不难发现:首先,点M的横坐标x应满足x>-5,即点M应在直线l的右边,否则点M到F的距离大于它到l的距离;其次,“点M与点F的距离比它到直线l:x+5=0的距离小1”,就是“点M与点F的距离等于它到直线x+4=0的距离”,由此可知点M的轨迹是以F为焦点,直线x+4= 0为准线的抛物线.
由已知条件可知,点M与点F的距离等于它到直线x+4=0的距离.根据抛物线的定义,点M的轨迹是以F(4,0)为焦点的抛物线.
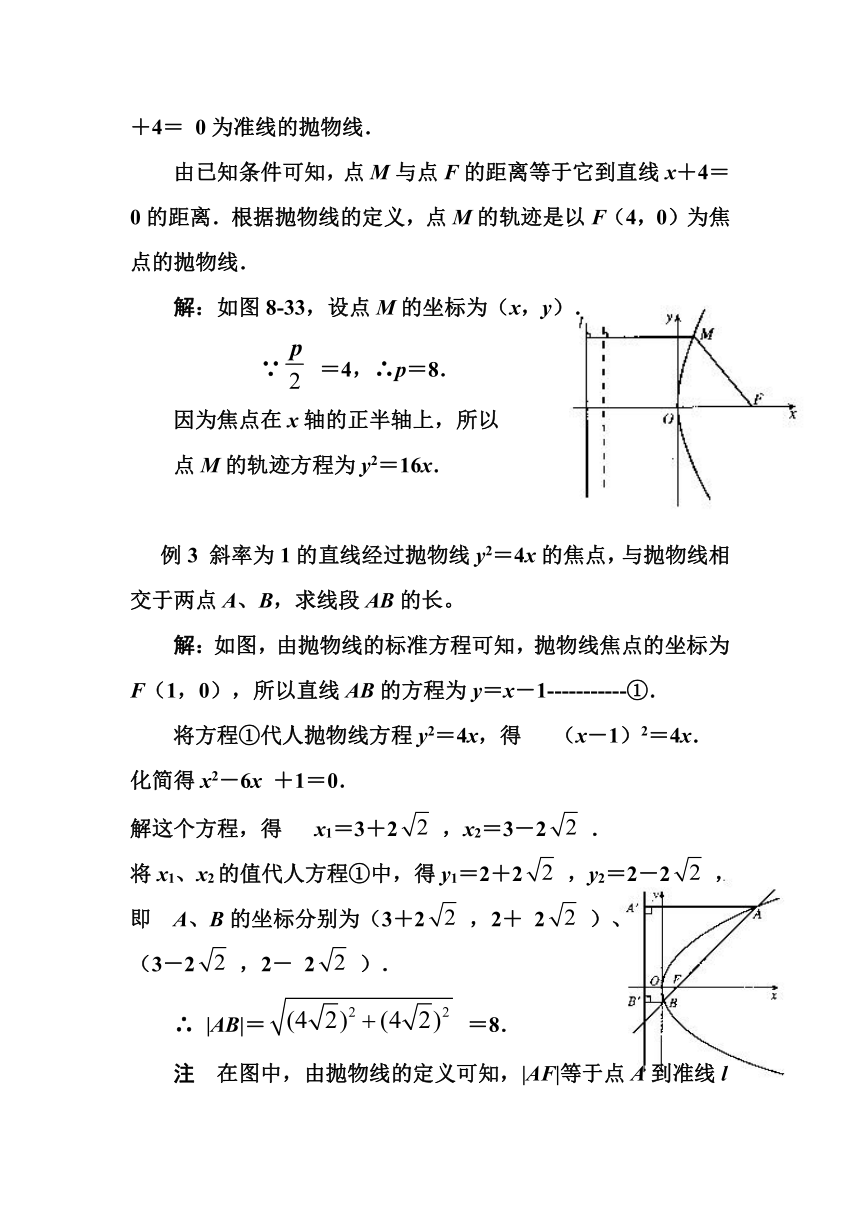
解:如图8-33,设点M的坐标为(x,y).
∵=4,∴p=8.
因为焦点在x轴的正半轴上,所以
点M的轨迹方程为y2=16x.
例3 斜率为1的直线经过抛物线y2=4x的焦点,与抛物线相交于两点A、B,求线段AB的长。
解:如图,由抛物线的标准方程可知,抛物线焦点的坐标为
F(1,0),所以直线AB的方程为y=x-1-----------①.
将方程①代人抛物线方程y2=4x,得 (x-1)2=4x.
化简得x2-6x +1=0.
解这个方程,得 x1=3+2,x2=3-2.
将x1、x2的值代人方程①中,得y1=2+2,y2=2-2,
即 A、B的坐标分别为(3+2,2+ 2)、
(3-2,2- 2).
∴ |AB|==8.
注 在图中,由抛物线的定义可知,|AF|等于点A到准线l的距离|AA′|,而|AA′|=x1+1.同理 |BF|=|BB′|=x2+1,于是得
|AB|=|AF|+|BF|=x1+x2+2.
由此可以看到,本题在得到方程x2-6x +1=0后,根据根与系数的关系可以直接得到x1+x2=6,于是立即可以求出|AB|=6+2=8.
补充题:
例1 求适合下列条件的抛物线的标准方程
(1)过点; (2)焦点在直线上;
解:(1)设抛物线的标准方程为
则将点代入上述方程得
(2)直线与坐标轴的交点为
所求抛物线方程为
例2.求证:以抛物线过焦点的弦为直径的圆必与此抛物线的准线相切。
证明:如图,过A、B分别作AC、BD垂直于,垂足为C、D
据抛物线的定义有
设M是AB的中点(即是其圆心)
过M作
则
例3.已知抛物线的顶点在原点,焦点在轴上,抛物线上一点到焦点的距离为5,求的值、抛物线的方程和准线的方程。
解:设抛物线方程为,则准线方程为,到准线的距离为5,
所以
又点
例4.如图所示,线段AB过轴正半轴上一点,端点到轴的距离之积为,以轴为对称轴,过三点作抛物线,求该抛物线的方程。
解:设所求抛物线方程为
若AB不垂直于轴,设AB方程
为
由(1)(2)消去,得
设A,B坐标为
则是方程(3)的两个根。
又,由
则抛物线的方程为
若AB轴,直线AB的方程为两点关于轴对称,故
例5 已知动圆M与直线相切,且与定圆外切,求动圆圆心的轨迹方程。
分析:设,由已知,则动圆圆心的方程是以为焦点,为准线的抛物线,易求得:
变题1 设动圆轴相切,且与定圆外切,求动圆圆心的轨迹方程。
解:当
变题2 设动圆轴相切,且与定圆相切,求动圆圆心的轨迹方程。
解:与圆外切时,当时,
与圆内切时,当当
1.平面上到定点距离相等的点的轨迹为( )
A.直线 B.抛物线 C.双曲线 D.椭圆
2.已知抛物线顶点在原点,对称轴为轴,焦点在曲线上,求抛物线的标准方程。
解:焦点坐标为,抛物线方程为
3.到定点的距离与到定直线的距离之比等于的点的轨迹是
A.圆 B.椭圆 C.双曲线 D.抛物线
4.顶点在原点,焦点是的抛物线方程是( )
A. B. C. D.
5.抛物线的准线方程是( )
A. B. C. D.
6.抛物线的顶点在原点,对称轴是轴,抛物线上一点到焦点距离是6,则抛物线的方程是( )
A. B. C. D.
7.过点的抛物线的标准方程是或
8.抛物线的顶点在坐标原点,焦点是椭圆的一个焦点,则此抛物线的焦点到准线的距离为( )
A. B. C. D.
9.在抛物线上有一点P,它到焦点的距离是20,则P点的坐标是
10.在抛物线上求一点P,使P到焦点F与到点的距离之和最小。
例 1 (1)已知抛物线的标准方程是 y2= 6x,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程.
解:(1)因为p=3,所以焦点坐标是(,0),准线方程是x=-.
(2)因为焦点在y轴的负半轴上,并且=2,p=4,所以所求抛物线的标准方程是
x2=-8y.
例2 点M与点F(4,0)的距离比它到直线l:x+5=0的距离小1,求点M的轨迹方程.
分析:由已知,点M属于集合 P={M||MF|+1=|x+5|}.
将|MF|用点的坐标表示出来,化简后就可得到点M的轨迹方程.但这种解法的化简过程比较烦琐.
仔细分析题目的条件,不难发现:首先,点M的横坐标x应满足x>-5,即点M应在直线l的右边,否则点M到F的距离大于它到l的距离;其次,“点M与点F的距离比它到直线l:x+5=0的距离小1”,就是“点M与点F的距离等于它到直线x+4=0的距离”,由此可知点M的轨迹是以F为焦点,直线x+4= 0为准线的抛物线.
由已知条件可知,点M与点F的距离等于它到直线x+4=0的距离.根据抛物线的定义,点M的轨迹是以F(4,0)为焦点的抛物线.
解:如图8-33,设点M的坐标为(x,y).
∵=4,∴p=8.
因为焦点在x轴的正半轴上,所以
点M的轨迹方程为y2=16x.
例3 斜率为1的直线经过抛物线y2=4x的焦点,与抛物线相交于两点A、B,求线段AB的长。
解:如图,由抛物线的标准方程可知,抛物线焦点的坐标为
F(1,0),所以直线AB的方程为y=x-1-----------①.
将方程①代人抛物线方程y2=4x,得 (x-1)2=4x.
化简得x2-6x +1=0.
解这个方程,得 x1=3+2,x2=3-2.
将x1、x2的值代人方程①中,得y1=2+2,y2=2-2,
即 A、B的坐标分别为(3+2,2+ 2)、
(3-2,2- 2).
∴ |AB|==8.
注 在图中,由抛物线的定义可知,|AF|等于点A到准线l的距离|AA′|,而|AA′|=x1+1.同理 |BF|=|BB′|=x2+1,于是得
|AB|=|AF|+|BF|=x1+x2+2.
由此可以看到,本题在得到方程x2-6x +1=0后,根据根与系数的关系可以直接得到x1+x2=6,于是立即可以求出|AB|=6+2=8.
补充题:
例1 求适合下列条件的抛物线的标准方程
(1)过点; (2)焦点在直线上;
解:(1)设抛物线的标准方程为
则将点代入上述方程得
(2)直线与坐标轴的交点为
所求抛物线方程为
例2.求证:以抛物线过焦点的弦为直径的圆必与此抛物线的准线相切。
证明:如图,过A、B分别作AC、BD垂直于,垂足为C、D
据抛物线的定义有
设M是AB的中点(即是其圆心)
过M作
则
例3.已知抛物线的顶点在原点,焦点在轴上,抛物线上一点到焦点的距离为5,求的值、抛物线的方程和准线的方程。
解:设抛物线方程为,则准线方程为,到准线的距离为5,
所以
又点
例4.如图所示,线段AB过轴正半轴上一点,端点到轴的距离之积为,以轴为对称轴,过三点作抛物线,求该抛物线的方程。
解:设所求抛物线方程为
若AB不垂直于轴,设AB方程
为
由(1)(2)消去,得
设A,B坐标为
则是方程(3)的两个根。
又,由
则抛物线的方程为
若AB轴,直线AB的方程为两点关于轴对称,故
例5 已知动圆M与直线相切,且与定圆外切,求动圆圆心的轨迹方程。
分析:设,由已知,则动圆圆心的方程是以为焦点,为准线的抛物线,易求得:
变题1 设动圆轴相切,且与定圆外切,求动圆圆心的轨迹方程。
解:当
变题2 设动圆轴相切,且与定圆相切,求动圆圆心的轨迹方程。
解:与圆外切时,当时,
与圆内切时,当当
1.平面上到定点距离相等的点的轨迹为( )
A.直线 B.抛物线 C.双曲线 D.椭圆
2.已知抛物线顶点在原点,对称轴为轴,焦点在曲线上,求抛物线的标准方程。
解:焦点坐标为,抛物线方程为
3.到定点的距离与到定直线的距离之比等于的点的轨迹是
A.圆 B.椭圆 C.双曲线 D.抛物线
4.顶点在原点,焦点是的抛物线方程是( )
A. B. C. D.
5.抛物线的准线方程是( )
A. B. C. D.
6.抛物线的顶点在原点,对称轴是轴,抛物线上一点到焦点距离是6,则抛物线的方程是( )
A. B. C. D.
7.过点的抛物线的标准方程是或
8.抛物线的顶点在坐标原点,焦点是椭圆的一个焦点,则此抛物线的焦点到准线的距离为( )
A. B. C. D.
9.在抛物线上有一点P,它到焦点的距离是20,则P点的坐标是
10.在抛物线上求一点P,使P到焦点F与到点的距离之和最小。
