抛物线2
图片预览

文档简介
抛物线
[知识盘点]
一.抛物线的概念
抛物线:平面内与一个定点和一条定直线的 的点的轨迹叫做抛物线,点叫做抛物线的 ,定直线叫做抛物线的 .
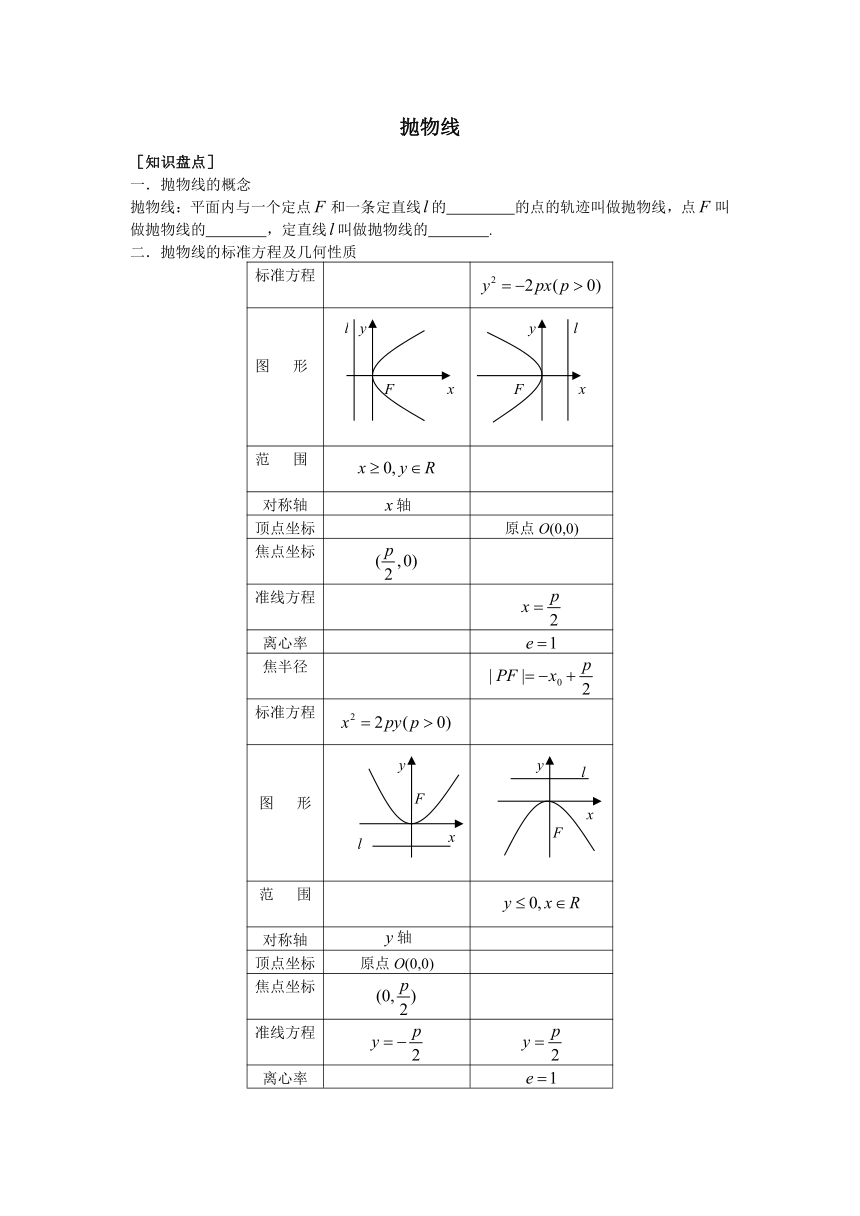
二.抛物线的标准方程及几何性质
标准方程
图 形
范 围
对称轴 轴
顶点坐标 原点O(0,0)
焦点坐标
准线方程
离心率
焦半径
标准方程
图 形
范 围
对称轴 轴
顶点坐标 原点O(0,0)
焦点坐标
准线方程
离心率
焦半径
三、研究讨论抛物线的有关性质
1.范围
2.对称性
3.顶点
4.离心率 抛物线上的点与焦点的距离和它到准线的距离的比,叫做抛物线的离心率,用表示.由抛物线的定义可知,.
5.通径:过焦点且垂直于对称轴的相交弦(图示)
直接应用抛物线定义,得到通径:
【典型例题与应用】
例1. 设是抛物线上的一动点,
(1)求点到点的距离与点到直线的距离之和的最小值;
(2)若,求的最小值.
例2、焦半径公式;
抛物线y2=2px (p>0)上一点M,则点M到准线的距离是_____,到焦点的距离是______________
应用:(1)抛物线x2=8y上的点P到焦点的距离是10,则P点坐标为_________
(2)过焦点的弦长|AB|
如果直线经过抛物线y2=2px(p>0)焦点,且交点为,则|AB|=____
变式练习:
1、抛物线y2=8px(p>0)上一点M到焦点的距离为a,则点M到y轴的距离为__________
2、经过抛物线的焦点,且与抛物线相交于两点,若=10,则|AB|=________________
例3.斜率为1的直线经过抛物线的焦点,且与抛物线相交于A,B两点,求线段AB的长。
例4已知抛物线,直线m过定点P(-2,1),斜率为k。当k为何值时,直线m与抛物线:只有一个公共点;有两个公共点;没有公共点。
【随堂练习】
1.设a≠0,a∈R,则抛物线y=4ax2的焦点坐标为 ( )
(A)(a,0) (B)(0,a) (C)(0,) (D)随a符号而定
2.以抛物线y2=2px(p>0)的焦半径|PF|为直径的圆与y轴位置关系为( )
(A)相交 (B)相离 (C)相切 (D)不确定
3.(2006年安徽卷)若抛物线的焦点与椭圆的右焦点重合,则的值为( )
A. B. C. D.
4.(2006年山东卷)已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于A(x1,y1),B(x2,y2)两点,则y12+y22的最小值是 .
5.设抛物线上一点到准线与对称轴的距离分别为10和6,则该点的横坐标为 。
6.(2005年重庆卷)连接抛物线上任意四点,组成的四边形可能是 (填写所有正确选项的序号)
①菱形 ②有3条件边相等的四边形 ③梯形 ④平行四边形 ⑤有一组对角相等的四边形
7、抛物线顶点坐标是____________焦点坐标是_______准线方程是______离心率是______,通径长是__________
抛物线上一点到焦点的距离为,则这点坐标________________
9根据下列条件,求抛物线的方程。
(1)顶点在原点,对称轴是x轴,顶点到焦点的距离等于8.
(2)顶点在原点,焦点在y轴上,且过P(4,2)点.(3)焦点在上
(4)顶点在原点,焦点在y轴上,其上点P(m,-3)到焦点距离为5.
(5)关于坐标轴对称,它的顶点在坐标原点,并且经过点M
10、抛物线顶点在原点,以坐标轴为对称轴,过焦点且与y轴垂直的弦长为16,求抛物线方程.
直线x-y=2与抛物线相交于A,B两点,(1)求;(2)求线段AB中点的坐标。
l
y
F
x
l
y
F
x
l
y
F
x
l
y
F
x
[知识盘点]
一.抛物线的概念
抛物线:平面内与一个定点和一条定直线的 的点的轨迹叫做抛物线,点叫做抛物线的 ,定直线叫做抛物线的 .
二.抛物线的标准方程及几何性质
标准方程
图 形
范 围
对称轴 轴
顶点坐标 原点O(0,0)
焦点坐标
准线方程
离心率
焦半径
标准方程
图 形
范 围
对称轴 轴
顶点坐标 原点O(0,0)
焦点坐标
准线方程
离心率
焦半径
三、研究讨论抛物线的有关性质
1.范围
2.对称性
3.顶点
4.离心率 抛物线上的点与焦点的距离和它到准线的距离的比,叫做抛物线的离心率,用表示.由抛物线的定义可知,.
5.通径:过焦点且垂直于对称轴的相交弦(图示)
直接应用抛物线定义,得到通径:
【典型例题与应用】
例1. 设是抛物线上的一动点,
(1)求点到点的距离与点到直线的距离之和的最小值;
(2)若,求的最小值.
例2、焦半径公式;
抛物线y2=2px (p>0)上一点M,则点M到准线的距离是_____,到焦点的距离是______________
应用:(1)抛物线x2=8y上的点P到焦点的距离是10,则P点坐标为_________
(2)过焦点的弦长|AB|
如果直线经过抛物线y2=2px(p>0)焦点,且交点为,则|AB|=____
变式练习:
1、抛物线y2=8px(p>0)上一点M到焦点的距离为a,则点M到y轴的距离为__________
2、经过抛物线的焦点,且与抛物线相交于两点,若=10,则|AB|=________________
例3.斜率为1的直线经过抛物线的焦点,且与抛物线相交于A,B两点,求线段AB的长。
例4已知抛物线,直线m过定点P(-2,1),斜率为k。当k为何值时,直线m与抛物线:只有一个公共点;有两个公共点;没有公共点。
【随堂练习】
1.设a≠0,a∈R,则抛物线y=4ax2的焦点坐标为 ( )
(A)(a,0) (B)(0,a) (C)(0,) (D)随a符号而定
2.以抛物线y2=2px(p>0)的焦半径|PF|为直径的圆与y轴位置关系为( )
(A)相交 (B)相离 (C)相切 (D)不确定
3.(2006年安徽卷)若抛物线的焦点与椭圆的右焦点重合,则的值为( )
A. B. C. D.
4.(2006年山东卷)已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于A(x1,y1),B(x2,y2)两点,则y12+y22的最小值是 .
5.设抛物线上一点到准线与对称轴的距离分别为10和6,则该点的横坐标为 。
6.(2005年重庆卷)连接抛物线上任意四点,组成的四边形可能是 (填写所有正确选项的序号)
①菱形 ②有3条件边相等的四边形 ③梯形 ④平行四边形 ⑤有一组对角相等的四边形
7、抛物线顶点坐标是____________焦点坐标是_______准线方程是______离心率是______,通径长是__________
抛物线上一点到焦点的距离为,则这点坐标________________
9根据下列条件,求抛物线的方程。
(1)顶点在原点,对称轴是x轴,顶点到焦点的距离等于8.
(2)顶点在原点,焦点在y轴上,且过P(4,2)点.(3)焦点在上
(4)顶点在原点,焦点在y轴上,其上点P(m,-3)到焦点距离为5.
(5)关于坐标轴对称,它的顶点在坐标原点,并且经过点M
10、抛物线顶点在原点,以坐标轴为对称轴,过焦点且与y轴垂直的弦长为16,求抛物线方程.
直线x-y=2与抛物线相交于A,B两点,(1)求;(2)求线段AB中点的坐标。
l
y
F
x
l
y
F
x
l
y
F
x
l
y
F
x
