双曲线
图片预览


文档简介
双曲线
[知识盘点]
1.双曲线的定义:我们把平面内与两个定点的距离的差的绝对值等于常数( )的点的轨迹叫做双曲线,用符号表示为 。这两个定点叫双曲线的 ,两个焦点之间的距离叫做双曲线的 。
2.双曲线的第二定义:平面内,到定点(或)的距离与到定直线 的距离之比是常数(即 )的动点的轨迹叫做双曲线,这个定点是双曲线的 ,这条定直线叫做双曲线的 ,其中常数叫做双曲线的 。
二.双曲线的标准方程
3.当双曲线的焦点在轴上时,双曲线的标准方程为 ,其中焦点坐标为,,且 ;
当双曲线的焦点在轴上时,双曲线的标准方程为 ,其中焦点坐标为,,且 .
当且仅当双曲线的中心在坐标原点,其焦点在坐标轴上时,双曲线的方程才是标准形式。
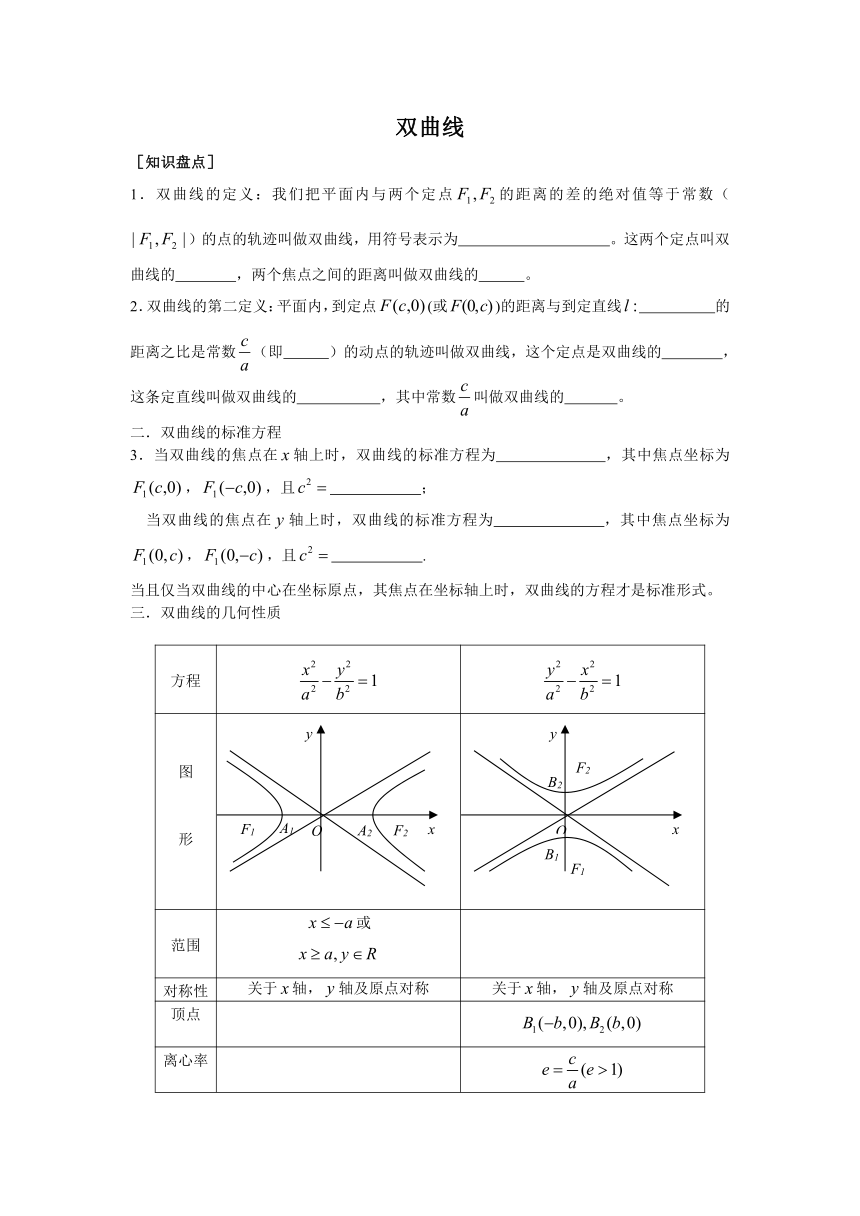
三.双曲线的几何性质
方程
图形
范围 或
对称性 关于轴,轴及原点对称 关于轴,轴及原点对称
顶点
离心率
准线
渐近线
[典例精析]
设双曲线与椭圆有共同的焦点,且与椭圆相交,一个交点的纵坐标为4,求双曲线的方程。
例2.设点P到点M(-1,0)、N(1,0)距离之差为2m,到x轴、y轴距离之比为2,求m的取值范围.
[剖析]由|PM|-|PN|=2m,得||PM|-|PN||=2|m|.知点P的轨迹是双曲线,由点P到x轴、y轴距离之比为2,知点P的轨迹是直线,由交轨法求得点P的坐标,进而可求得m的取值 范围.
例3.已知双曲线C的中心在原点,焦点在轴上,点与其渐近线的距离为,过点P作斜率为的直线交双曲线于两点,交轴于M,且是与的等比中项.
(1)求双曲线的渐近线方程;
(2)求双曲线的方程.
[剖析](1)由点与其渐近线的距离为,借助于点到直线的距离公式可求得其渐近线方程;(2)由渐近线方程,可设双曲线方程,再借助于题条件,不难得到双曲线方程。
过双曲线的右焦点,倾斜角为的直线交双曲线于两点,求两点的坐标。(变训练:求及的周长,)
(解几问题,求两曲线的交点,一般是通过联立方程组求解)
例5、已知双曲线的焦点在轴上,方程为,两顶点的距离为8,一渐近线上有点
,试求此双曲线的方程。
【随堂练习】
一、选择题(每小题四个选项中,只有一项符合题目要求)
1.已知点和,曲线上的动点P到、的距离之差为6,则曲线方程为( )
A.
B.
C.或
D.
2.“ab<0”是“方程表示双曲线”的( )
A.必要不充分条件
B.充分不必要条件
C.充要条件
D.既不充分又不必要条件
3.动圆与两圆和都相切,则动圆圆心的轨迹为( )
A.抛物线
B.圆
C.双曲线的一支
D.椭圆
4.P为双曲线上的一点,F为一个焦点,以PF为直径的圆与圆的位置关系是( )
A.内切
B.内切或外切
C.外切
D.相离或相交
5.双曲线的左焦点为F,点P为左支的下半支上任一点(非顶点),则直线PF的斜率的范围是( )
A.(-∞,0]∪[1,+∞)
B.(-∞,0)∪(1,+∞)
C.(-∞,-1)∪[1,+∞)
D.(-∞,-1)∪(1,+∞)
6.若椭圆和双曲线有相同的焦点、,P是两曲线的一个公共点,则的值是( )
A.m-a B.
C. D.
二、填空题
7.双曲线的一个焦点是,则m的值是_________。
8.过双曲线的焦点且垂直于x轴的弦的长度为_______。
三、解答题
9.已知双曲线过点A(-2,4)、B(4,4),它的一个焦点是,求它的另一个焦点的轨迹方程。
10.已知直线y=ax+1与双曲线相交于A、B两点,是否存在这样的实数a,使得A、B关于直线y=2x对称?如果存在,求出a的值,如果不存在,说明理由。
11.A、B、C是我方三个炮兵阵地,A在B的正东相距6km,C在B的北偏西30°相距4km,P为敌炮兵阵地,某时刻A发现敌炮阵地的某种信号,4秒种后,B、C才同时发现这一信号,该信号的传播速度为每秒1km,A若炮击P地,求炮击的方位角。
答案与提示
一、1.D
2.A
3.C
4.B
5.B
6.A
二、7.-2
8.
三、9.提示:易知
由双曲线定义知
即
① 即
此时点的轨迹为线段AB的中垂线,其方程为x=1(y≠0)
② 即
此时点的轨迹为以A、B为焦点,长轴长为10的椭圆,其方程为 (y≠0)
10.不存在
11.提示:以AB的中点为原点,正东、正北方向分别为x轴、y轴建立直角坐标系,则A(3,0),B(-3,0),,依题意|PB|-|PA|=4
∴ P点在以A、B为焦点的双曲线的右支上,其中c=3,2a=4,则,方程为
又|PB|=|PC| ∴P在线段BC的垂直平分线上
联立解得 ∴
又 ∴α=60°
∴P点在A点东偏北60°处,即A炮击P地时,炮击的方位角为北偏东30°
y
O
A1
F1
A2
F2
x
y
O
B1
F1
B2
F2
x
[知识盘点]
1.双曲线的定义:我们把平面内与两个定点的距离的差的绝对值等于常数( )的点的轨迹叫做双曲线,用符号表示为 。这两个定点叫双曲线的 ,两个焦点之间的距离叫做双曲线的 。
2.双曲线的第二定义:平面内,到定点(或)的距离与到定直线 的距离之比是常数(即 )的动点的轨迹叫做双曲线,这个定点是双曲线的 ,这条定直线叫做双曲线的 ,其中常数叫做双曲线的 。
二.双曲线的标准方程
3.当双曲线的焦点在轴上时,双曲线的标准方程为 ,其中焦点坐标为,,且 ;
当双曲线的焦点在轴上时,双曲线的标准方程为 ,其中焦点坐标为,,且 .
当且仅当双曲线的中心在坐标原点,其焦点在坐标轴上时,双曲线的方程才是标准形式。
三.双曲线的几何性质
方程
图形
范围 或
对称性 关于轴,轴及原点对称 关于轴,轴及原点对称
顶点
离心率
准线
渐近线
[典例精析]
设双曲线与椭圆有共同的焦点,且与椭圆相交,一个交点的纵坐标为4,求双曲线的方程。
例2.设点P到点M(-1,0)、N(1,0)距离之差为2m,到x轴、y轴距离之比为2,求m的取值范围.
[剖析]由|PM|-|PN|=2m,得||PM|-|PN||=2|m|.知点P的轨迹是双曲线,由点P到x轴、y轴距离之比为2,知点P的轨迹是直线,由交轨法求得点P的坐标,进而可求得m的取值 范围.
例3.已知双曲线C的中心在原点,焦点在轴上,点与其渐近线的距离为,过点P作斜率为的直线交双曲线于两点,交轴于M,且是与的等比中项.
(1)求双曲线的渐近线方程;
(2)求双曲线的方程.
[剖析](1)由点与其渐近线的距离为,借助于点到直线的距离公式可求得其渐近线方程;(2)由渐近线方程,可设双曲线方程,再借助于题条件,不难得到双曲线方程。
过双曲线的右焦点,倾斜角为的直线交双曲线于两点,求两点的坐标。(变训练:求及的周长,)
(解几问题,求两曲线的交点,一般是通过联立方程组求解)
例5、已知双曲线的焦点在轴上,方程为,两顶点的距离为8,一渐近线上有点
,试求此双曲线的方程。
【随堂练习】
一、选择题(每小题四个选项中,只有一项符合题目要求)
1.已知点和,曲线上的动点P到、的距离之差为6,则曲线方程为( )
A.
B.
C.或
D.
2.“ab<0”是“方程表示双曲线”的( )
A.必要不充分条件
B.充分不必要条件
C.充要条件
D.既不充分又不必要条件
3.动圆与两圆和都相切,则动圆圆心的轨迹为( )
A.抛物线
B.圆
C.双曲线的一支
D.椭圆
4.P为双曲线上的一点,F为一个焦点,以PF为直径的圆与圆的位置关系是( )
A.内切
B.内切或外切
C.外切
D.相离或相交
5.双曲线的左焦点为F,点P为左支的下半支上任一点(非顶点),则直线PF的斜率的范围是( )
A.(-∞,0]∪[1,+∞)
B.(-∞,0)∪(1,+∞)
C.(-∞,-1)∪[1,+∞)
D.(-∞,-1)∪(1,+∞)
6.若椭圆和双曲线有相同的焦点、,P是两曲线的一个公共点,则的值是( )
A.m-a B.
C. D.
二、填空题
7.双曲线的一个焦点是,则m的值是_________。
8.过双曲线的焦点且垂直于x轴的弦的长度为_______。
三、解答题
9.已知双曲线过点A(-2,4)、B(4,4),它的一个焦点是,求它的另一个焦点的轨迹方程。
10.已知直线y=ax+1与双曲线相交于A、B两点,是否存在这样的实数a,使得A、B关于直线y=2x对称?如果存在,求出a的值,如果不存在,说明理由。
11.A、B、C是我方三个炮兵阵地,A在B的正东相距6km,C在B的北偏西30°相距4km,P为敌炮兵阵地,某时刻A发现敌炮阵地的某种信号,4秒种后,B、C才同时发现这一信号,该信号的传播速度为每秒1km,A若炮击P地,求炮击的方位角。
答案与提示
一、1.D
2.A
3.C
4.B
5.B
6.A
二、7.-2
8.
三、9.提示:易知
由双曲线定义知
即
① 即
此时点的轨迹为线段AB的中垂线,其方程为x=1(y≠0)
② 即
此时点的轨迹为以A、B为焦点,长轴长为10的椭圆,其方程为 (y≠0)
10.不存在
11.提示:以AB的中点为原点,正东、正北方向分别为x轴、y轴建立直角坐标系,则A(3,0),B(-3,0),,依题意|PB|-|PA|=4
∴ P点在以A、B为焦点的双曲线的右支上,其中c=3,2a=4,则,方程为
又|PB|=|PC| ∴P在线段BC的垂直平分线上
联立解得 ∴
又 ∴α=60°
∴P点在A点东偏北60°处,即A炮击P地时,炮击的方位角为北偏东30°
y
O
A1
F1
A2
F2
x
y
O
B1
F1
B2
F2
x
