2020-2021学年人教版八年级下册数学第18章《平行四边形》(Word版 含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学第18章《平行四边形》(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 257.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-17 15:41:40 | ||
图片预览


文档简介
第18章
《平行四边形》单元测试
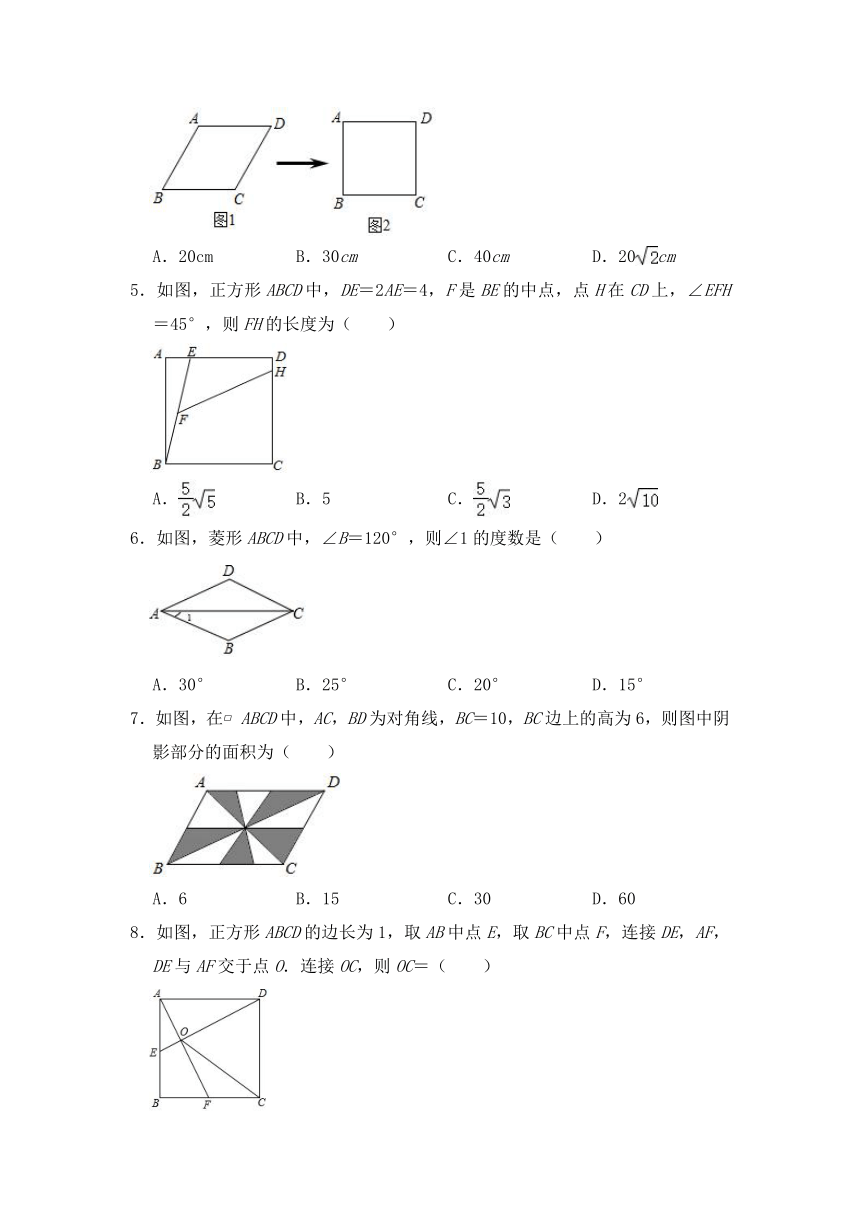
一.选择题(每题3分,共30分)
1.如图,在菱形ABCD中,∠ABC=80°,E是线段BD上一动点(点E不与点B,D重合),当△ABE是等腰三角形时,∠DAE=( )
A.30°
B.70°
C.30°或60°
D.40°或70°
2.如图,菱形ABCD的边AB的垂直平分线交AB于点E,交AC于点F,连接DF.当∠BAD=100°时,则∠CDF=( )
A.15°
B.30°
C.40°
D.50°
3.如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
A.20°
B.30°
C.35°
D.55°
4.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm
B.30cm
C.40cm
D.20cm
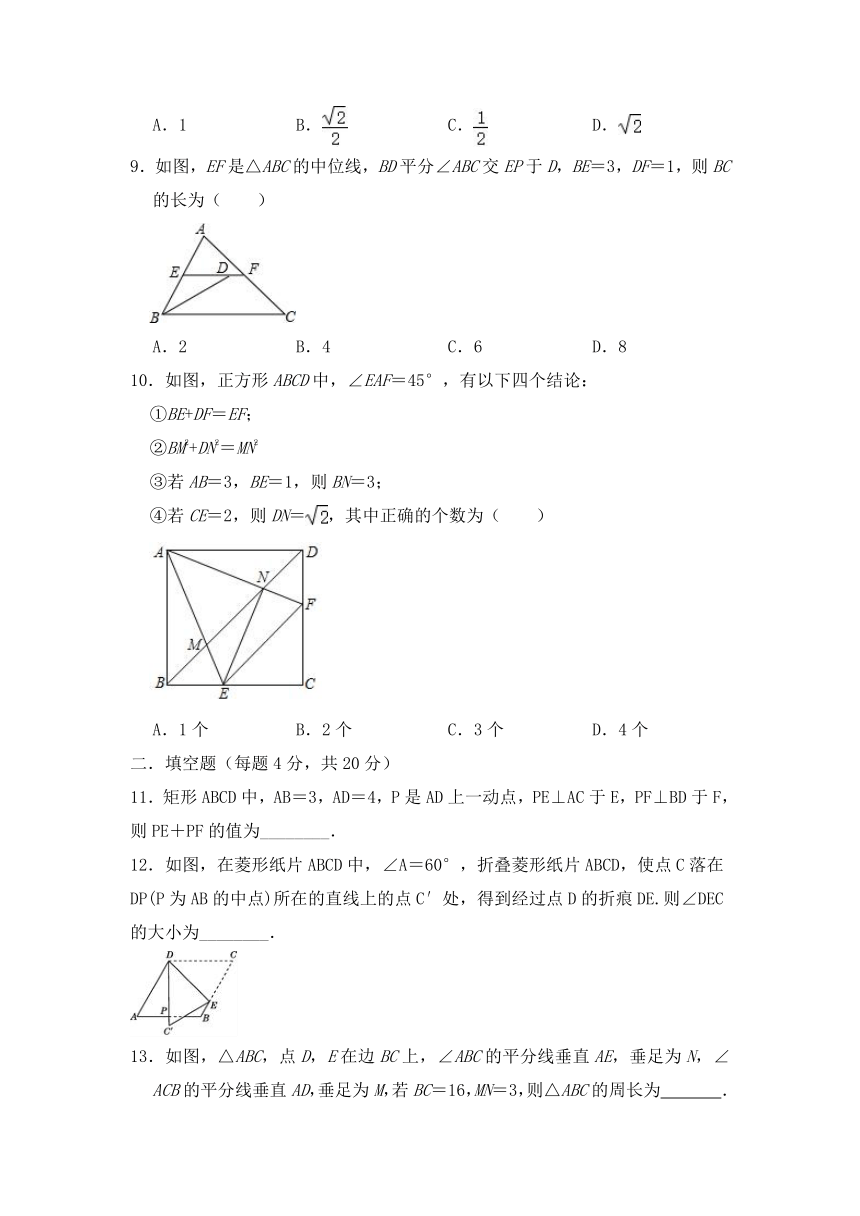
5.如图,正方形ABCD中,DE=2AE=4,F是BE的中点,点H在CD上,∠EFH=45°,则FH的长度为( )
A.
B.5
C.
D.2
6.如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30°
B.25°
C.20°
D.15°
7.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6
B.15
C.30
D.60
8.如图,正方形ABCD的边长为1,取AB中点E,取BC中点F,连接DE,AF,DE与AF交于点O.连接OC,则OC=( )
A.1
B.
C.
D.
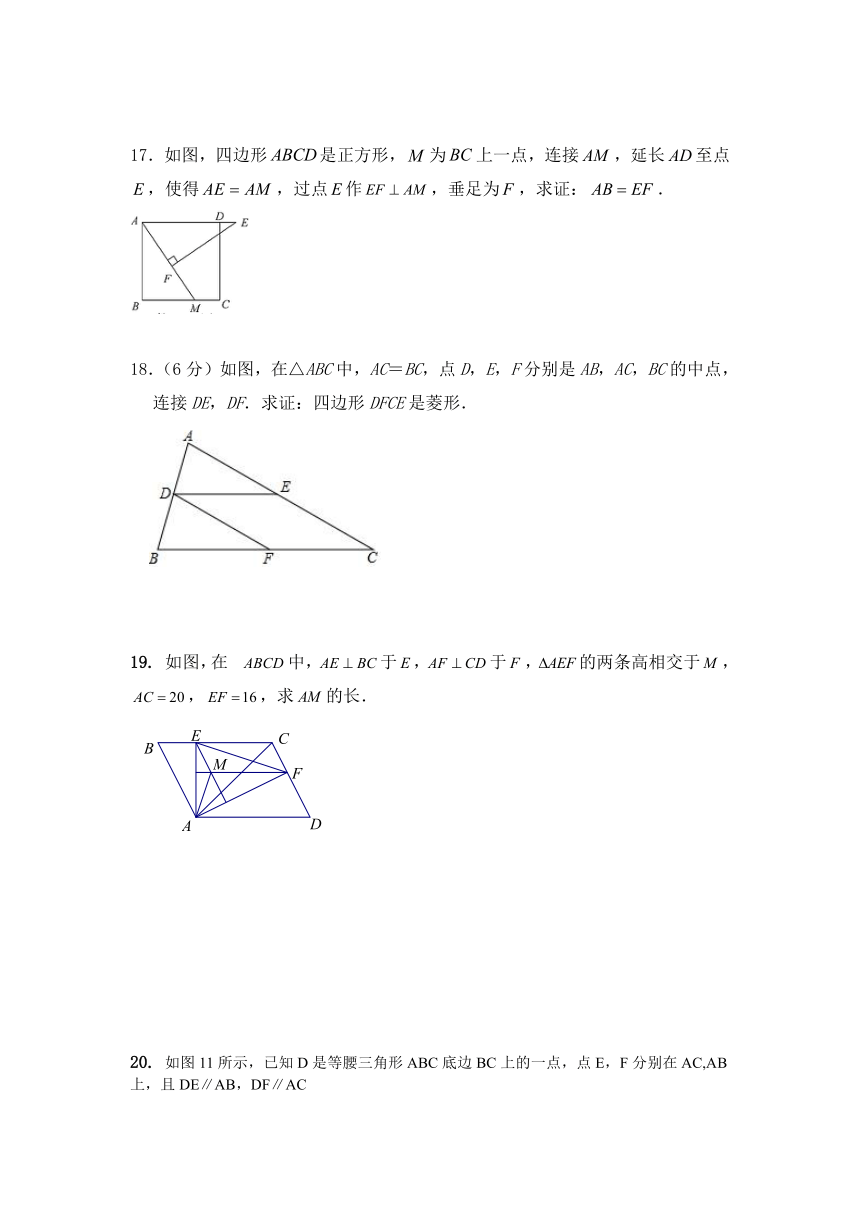
9.如图,EF是△ABC的中位线,BD平分∠ABC交EP于D,BE=3,DF=1,则BC的长为( )
A.2
B.4
C.6
D.8
10.如图,正方形ABCD中,∠EAF=45°,有以下四个结论:
①BE+DF=EF;
②BM2+DN2=MN2
③若AB=3,BE=1,则BN=3;
④若CE=2,则DN=,其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
二.填空题(每题4分,共20分)
11.矩形ABCD中,AB=3,AD=4,P是AD上一动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为________.
12.如图,在菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB的中点)所在的直线上的点C′处,得到经过点D的折痕DE.则∠DEC的大小为________.
13.如图,△ABC,点D,E在边BC上,∠ABC的平分线垂直AE,垂足为N,∠ACB的平分线垂直AD,垂足为M,若BC=16,MN=3,则△ABC的周长为
.
14.如图,在平面直角坐标系中,菱形OABC的顶点B的坐标为(8,4),则C点的坐标为________.
(第14题)
15.如图,在边长为1的菱形ABCD中,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连接AE,再以AE为边作第三个菱形AEGH,使∠HAE=60°……按此规律所作的第n个菱形的边长是________.
(第15题)
三.解答题(每题10分,共50分)
16.如图,将长方形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.
(1)试写出图中若干相等的线段和锐角(分别写两对);
(2)证明:△ADF≌△AB′E.
17.如图,四边形是正方形,为上一点,连接,延长至点,使得,过点作,垂足为,求证:.
18.(6分)如图,在△ABC中,AC=BC,点D,E,F分别是AB,AC,BC的中点,连接DE,DF.求证:四边形DFCE是菱形.
19.
如图,在中,于,于,的两条高相交于,,,求的长.
20.
如图11所示,已知D是等腰三角形ABC底边BC上的一点,点E,F分别在AC,AB上,且DE∥AB,DF∥AC
求证:DE+DF=AB
21.如图,
在中,点、分别为、的中点,点在的延长线上,.
求证:.
22.已知:如图,在平行四边形ABCD中,点E是边AD上一点,分别连接BE,CE,若点F,G,H分别是EC,BC,BE的中点.
(1)求证:四边形EFGH是平行四边形;
(2)设四边形EFGH的面积为S1,四边形ABCD的面积为S2,请直接写出S1∶S2的值.
23.如图,AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC,交BC于F,试说明EC=EF=BF.
参考答案
一.选择题
1.C
2.B
3.
A
4.
C.
5.
D.
6.
C.
7.
C.
8.
A.
9.
D.10.C
二.填空题(共5小题)
11.
12.
75°
13.
38.
14.
(3,4)
15.
()n-1
三.解答题(共5小题)
16.证明:(1)由题意可得:∠D=∠B,∠B=∠B′;AD=CB,CB=AB′;
(2)∵四边形ABCD是长方形,
∴∠D=∠B=∠B′=90°,AD=CB=AB′,
∵∠DAF+∠EAF=90°,∠B′AE+∠EAF=90°,
∴∠DAF=∠B′AE,
在△ADF和△AB′E中,
,
∴△ADF≌△AB′E(ASA).
17.证明:四边形为正方形,
,,
,
,
,
在和中,,
,
.
18.证明:∵点D,E,F分别是AB,AC,BC的中点,
∴DE∥CF,DE=BC,DF∥CE,DF=AC,
∴四边形DECF是平行四边形,
∵AC=BC,
∴DE=DF,
∴四边形DFCE是菱形;
19.
【答案】
20.证明:∵DE∥AB,DF∥AC
∴四边形AEDF是平行四边形,∴DF=AE,又∵DE∥AB,∴∠B=∠EDC,又∵AB=AC,∴∠B=∠C,∴∠C=∠EDC,∴DE=CE,∴DF+DE=AE+CE=AC=AB.
21.∵在中,点、分别为、的中点
∴是的中位线
∴
即
∵
∴四边形为平行四边形
∴.
22.
(1)∵点F,G,H分别是EC,BC,BE的中点;
∴GFBE,且GF=BE=HE;
∴四边形EFGH是平行四边形;
(2)∵点F,H分别是EC,BE的中点,连接GE;
∴,,,
∴:=1∶4
23.在Rt△AEF和Rt△ABF中,
,
∴Rt△AEF≌Rt△ABF(HL),
∴FE=FB.
∵正方形ABCD,
∴∠ACB=∠BCD=45°,
在Rt△CEF中,
∵∠ACB=45°,
∴∠CFE=45°,
∴∠ACB=∠CFE,
∴EC=EF,
∴FB=EC=EF.
图11
《平行四边形》单元测试
一.选择题(每题3分,共30分)
1.如图,在菱形ABCD中,∠ABC=80°,E是线段BD上一动点(点E不与点B,D重合),当△ABE是等腰三角形时,∠DAE=( )
A.30°
B.70°
C.30°或60°
D.40°或70°
2.如图,菱形ABCD的边AB的垂直平分线交AB于点E,交AC于点F,连接DF.当∠BAD=100°时,则∠CDF=( )
A.15°
B.30°
C.40°
D.50°
3.如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
A.20°
B.30°
C.35°
D.55°
4.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm
B.30cm
C.40cm
D.20cm
5.如图,正方形ABCD中,DE=2AE=4,F是BE的中点,点H在CD上,∠EFH=45°,则FH的长度为( )
A.
B.5
C.
D.2
6.如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30°
B.25°
C.20°
D.15°
7.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6
B.15
C.30
D.60
8.如图,正方形ABCD的边长为1,取AB中点E,取BC中点F,连接DE,AF,DE与AF交于点O.连接OC,则OC=( )
A.1
B.
C.
D.
9.如图,EF是△ABC的中位线,BD平分∠ABC交EP于D,BE=3,DF=1,则BC的长为( )
A.2
B.4
C.6
D.8
10.如图,正方形ABCD中,∠EAF=45°,有以下四个结论:
①BE+DF=EF;
②BM2+DN2=MN2
③若AB=3,BE=1,则BN=3;
④若CE=2,则DN=,其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
二.填空题(每题4分,共20分)
11.矩形ABCD中,AB=3,AD=4,P是AD上一动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为________.
12.如图,在菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB的中点)所在的直线上的点C′处,得到经过点D的折痕DE.则∠DEC的大小为________.
13.如图,△ABC,点D,E在边BC上,∠ABC的平分线垂直AE,垂足为N,∠ACB的平分线垂直AD,垂足为M,若BC=16,MN=3,则△ABC的周长为
.
14.如图,在平面直角坐标系中,菱形OABC的顶点B的坐标为(8,4),则C点的坐标为________.
(第14题)
15.如图,在边长为1的菱形ABCD中,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连接AE,再以AE为边作第三个菱形AEGH,使∠HAE=60°……按此规律所作的第n个菱形的边长是________.
(第15题)
三.解答题(每题10分,共50分)
16.如图,将长方形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.
(1)试写出图中若干相等的线段和锐角(分别写两对);
(2)证明:△ADF≌△AB′E.
17.如图,四边形是正方形,为上一点,连接,延长至点,使得,过点作,垂足为,求证:.
18.(6分)如图,在△ABC中,AC=BC,点D,E,F分别是AB,AC,BC的中点,连接DE,DF.求证:四边形DFCE是菱形.
19.
如图,在中,于,于,的两条高相交于,,,求的长.
20.
如图11所示,已知D是等腰三角形ABC底边BC上的一点,点E,F分别在AC,AB上,且DE∥AB,DF∥AC
求证:DE+DF=AB
21.如图,
在中,点、分别为、的中点,点在的延长线上,.
求证:.
22.已知:如图,在平行四边形ABCD中,点E是边AD上一点,分别连接BE,CE,若点F,G,H分别是EC,BC,BE的中点.
(1)求证:四边形EFGH是平行四边形;
(2)设四边形EFGH的面积为S1,四边形ABCD的面积为S2,请直接写出S1∶S2的值.
23.如图,AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC,交BC于F,试说明EC=EF=BF.
参考答案
一.选择题
1.C
2.B
3.
A
4.
C.
5.
D.
6.
C.
7.
C.
8.
A.
9.
D.10.C
二.填空题(共5小题)
11.
12.
75°
13.
38.
14.
(3,4)
15.
()n-1
三.解答题(共5小题)
16.证明:(1)由题意可得:∠D=∠B,∠B=∠B′;AD=CB,CB=AB′;
(2)∵四边形ABCD是长方形,
∴∠D=∠B=∠B′=90°,AD=CB=AB′,
∵∠DAF+∠EAF=90°,∠B′AE+∠EAF=90°,
∴∠DAF=∠B′AE,
在△ADF和△AB′E中,
,
∴△ADF≌△AB′E(ASA).
17.证明:四边形为正方形,
,,
,
,
,
在和中,,
,
.
18.证明:∵点D,E,F分别是AB,AC,BC的中点,
∴DE∥CF,DE=BC,DF∥CE,DF=AC,
∴四边形DECF是平行四边形,
∵AC=BC,
∴DE=DF,
∴四边形DFCE是菱形;
19.
【答案】
20.证明:∵DE∥AB,DF∥AC
∴四边形AEDF是平行四边形,∴DF=AE,又∵DE∥AB,∴∠B=∠EDC,又∵AB=AC,∴∠B=∠C,∴∠C=∠EDC,∴DE=CE,∴DF+DE=AE+CE=AC=AB.
21.∵在中,点、分别为、的中点
∴是的中位线
∴
即
∵
∴四边形为平行四边形
∴.
22.
(1)∵点F,G,H分别是EC,BC,BE的中点;
∴GFBE,且GF=BE=HE;
∴四边形EFGH是平行四边形;
(2)∵点F,H分别是EC,BE的中点,连接GE;
∴,,,
∴:=1∶4
23.在Rt△AEF和Rt△ABF中,
,
∴Rt△AEF≌Rt△ABF(HL),
∴FE=FB.
∵正方形ABCD,
∴∠ACB=∠BCD=45°,
在Rt△CEF中,
∵∠ACB=45°,
∴∠CFE=45°,
∴∠ACB=∠CFE,
∴EC=EF,
∴FB=EC=EF.
图11
