矩形的定义和性质
图片预览


文档简介
(共17张PPT)
19.2.1 特殊的平行四边形 ----矩形的定义和性质
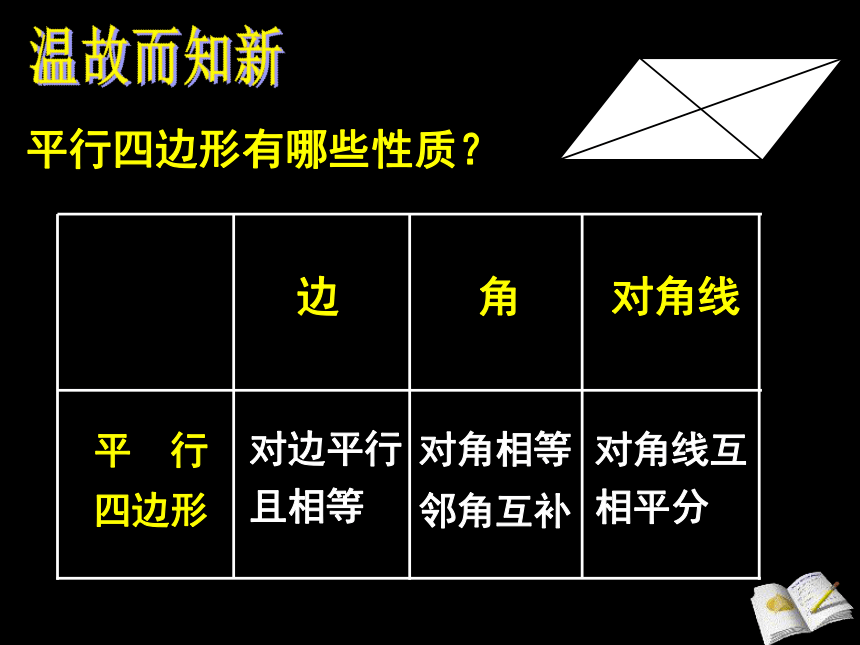
平行四边形有哪些性质?
平 行
四边形
对角线
角
边
对边平行且相等
对角相等
邻角互补
对角线互相平分
(1)拉动平行四边形的一个顶点后,该四边形还是平行四边形吗?为什么?
(2)在拉动的过程中,出现了什么特殊的图形?此时平行四边形的内角多少度?
请大家拿出自制的平行四边形学具 ,两人一组活动 . 拉动平行四边形的一个顶点,观察该变化过程并思考以下问题:
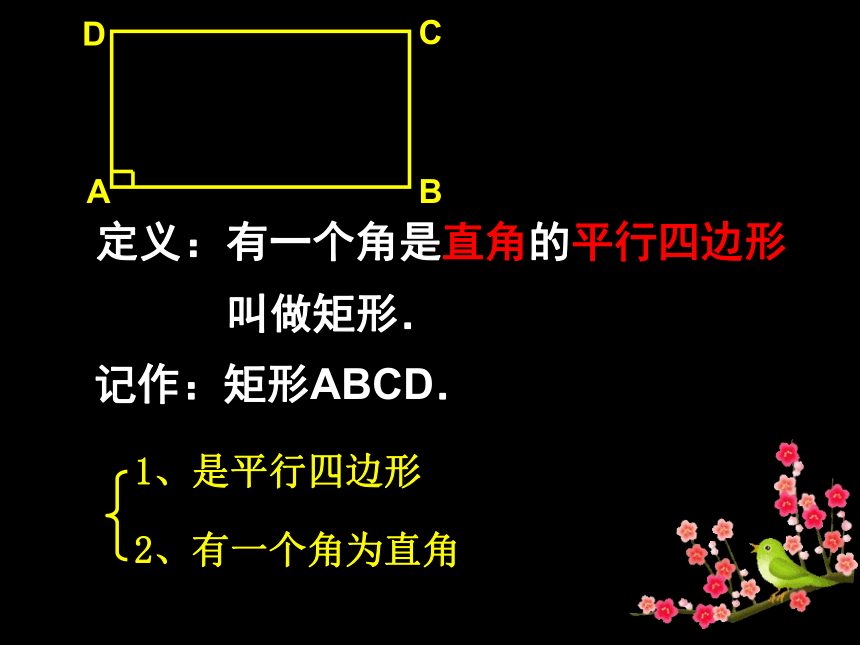
什么样的平行四边形可以称为矩形呢?
定义:有一个角是直角的平行四边形
叫做矩形.
2、有一个角为直角
1、是平行四边形
A
D
C
B
记作:矩形ABCD.
对角线
角
边
平 行
四边形
对边平行且相等
对角相等
邻角互补
对角线互相平分
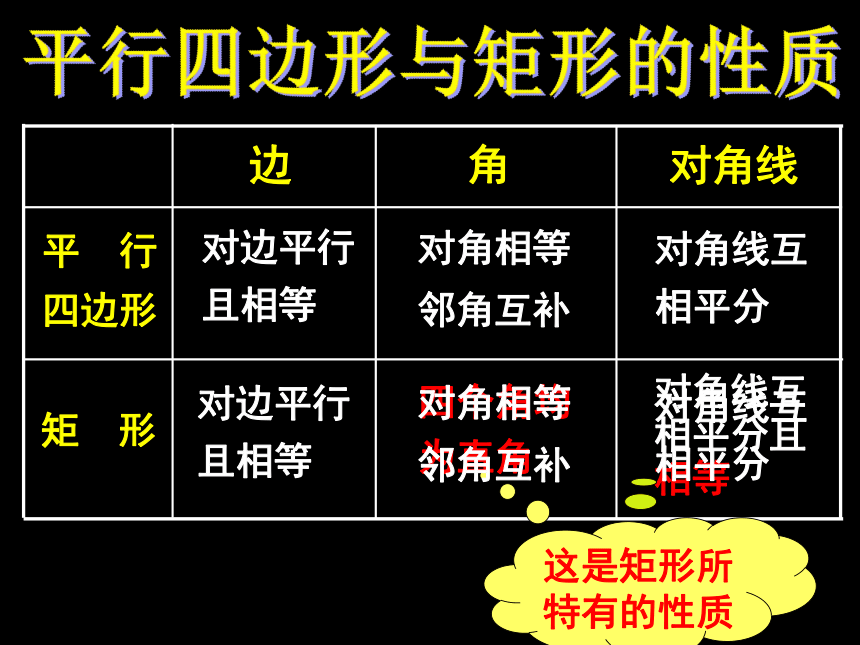
矩 形
对边平行且相等
四个角均为直角
对角线互相平分且相等
这是矩形所特有的性质
对角相等
邻角互补
对角线互相平分
A
O
D
C
B
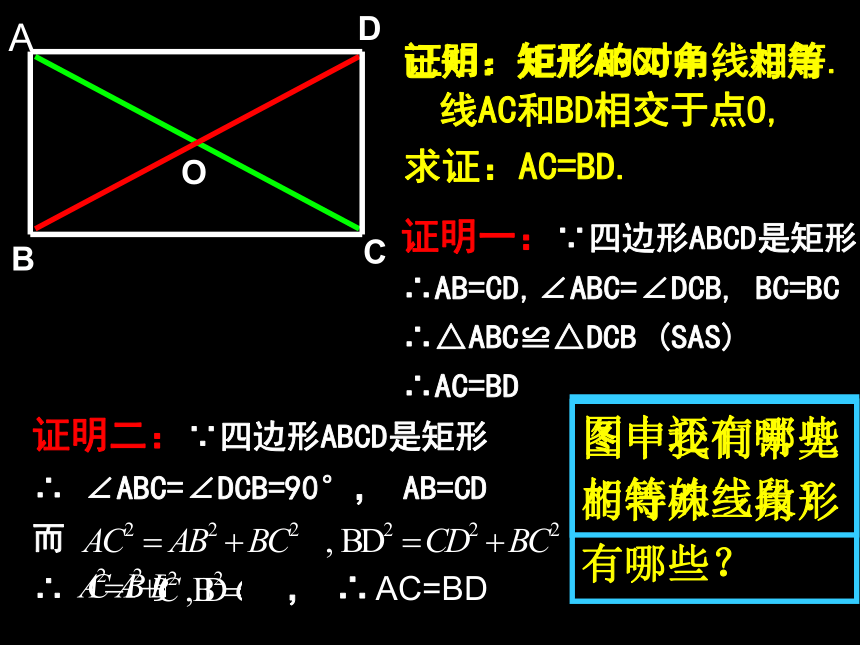
已知:矩形ABCD中,对角线AC和BD相交于点O,
求证:AC=BD.
证明一:∵四边形ABCD是矩形
∴AB=CD,∠ABC=∠DCB, BC=BC
∴△ABC≌△DCB (SAS)
∴AC=BD
证明二:∵四边形ABCD是矩形
∴ ∠ABC=∠DCB=90°, AB=CD
而
∴ , ∴ AC=BD
A
图中还有哪些相等的线段?
证明:矩形的对角线相等.
图中我们常见的特殊三角形有哪些?
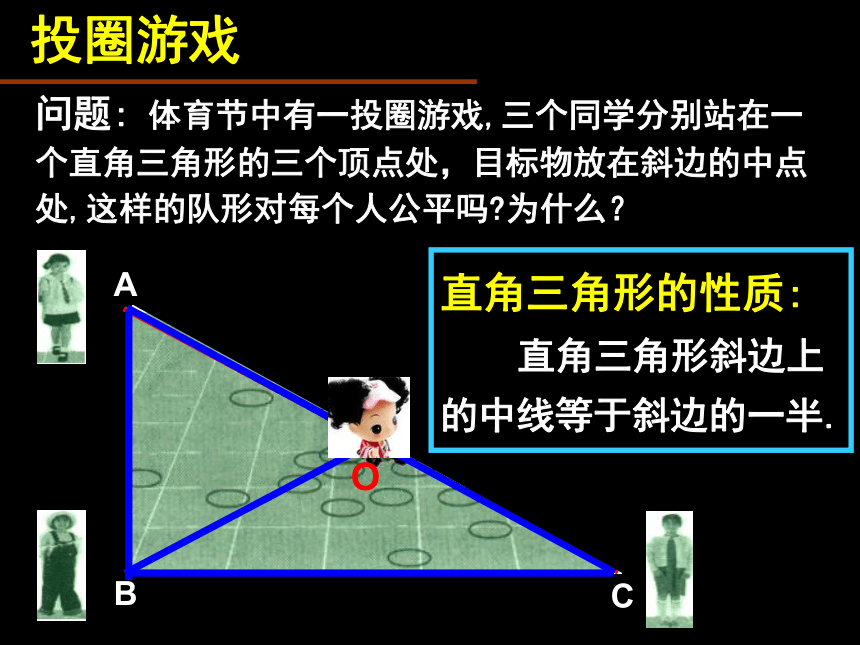
投圈游戏
问题: 体育节中有一投圈游戏,三个同学分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处,这样的队形对每个人公平吗 为什么?
B
C
D
A
O
直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半.
即兴练一练:
1.直角三角形两直角边分别为6和8,则其斜边上的中线长为________.
2.直角三角形两直角边分别为7和24,则其斜边上的中线长为________.
3.直角三角形两直角边分别为8和15,则其斜边上的中线长为________.
5
12.5
8.5
1.矩形具有而一般平行四边形不具有的性质是( ).
A、对角线相等 B、对边相等
C、对角相等 D、对角线互相平分
A
2.下面性质中,矩形不一定具有的是:( )
A、对角线相等 B、四个角都相等
C、是轴对称图形 D、对角线互相垂直
D
例1 如图,矩形ABCD的两条对角线交于点O, AB= 4cm ,∠AOD=120°, 求矩形对角线的长.
D
C
B
A
O
解矩形题时往往要注意:
1.矩形问题 三角形问题.
2.利用直角三角形的一些结论.
转化
1、矩形ABCD中,AC、BD相交于点O,AB=6,BC=8,则△ABO的周长为_____.
A
D
C
B
O
16
A
D
C
B
E
2、如图,矩形ABCD中,AE平分∠BAD交BC
于点E,ED=5cm,EC=3cm,求矩形的周长。
矩形问题
转 化
直角三角形问题
4、矩形问题 三角形问题.
3、直角三角形的一个重要性质:
直角三角形中,斜边上的中线等于斜边的一半.
1、矩形定义:
有一个角是直角的平行四边形叫矩形.
对边平行且相等
四个角均为直角
2、矩形
对角线互相平分且相等
转 化
3、(选做题)如图所示,锐角△ABC中,BE,CF是高,点M,N分别为BC,EF中点.求证:MN⊥EF.
1、(必做题)教材96面练习题:1、2题.
2、(必做题)如图,矩形ABCD的对角线交于点O,OF⊥BC,CE⊥BD, OF=4, OE∶BE=1∶3,求∠ADB 和 BD 的长.
19.2.1 特殊的平行四边形 ----矩形的定义和性质
平行四边形有哪些性质?
平 行
四边形
对角线
角
边
对边平行且相等
对角相等
邻角互补
对角线互相平分
(1)拉动平行四边形的一个顶点后,该四边形还是平行四边形吗?为什么?
(2)在拉动的过程中,出现了什么特殊的图形?此时平行四边形的内角多少度?
请大家拿出自制的平行四边形学具 ,两人一组活动 . 拉动平行四边形的一个顶点,观察该变化过程并思考以下问题:
什么样的平行四边形可以称为矩形呢?
定义:有一个角是直角的平行四边形
叫做矩形.
2、有一个角为直角
1、是平行四边形
A
D
C
B
记作:矩形ABCD.
对角线
角
边
平 行
四边形
对边平行且相等
对角相等
邻角互补
对角线互相平分
矩 形
对边平行且相等
四个角均为直角
对角线互相平分且相等
这是矩形所特有的性质
对角相等
邻角互补
对角线互相平分
A
O
D
C
B
已知:矩形ABCD中,对角线AC和BD相交于点O,
求证:AC=BD.
证明一:∵四边形ABCD是矩形
∴AB=CD,∠ABC=∠DCB, BC=BC
∴△ABC≌△DCB (SAS)
∴AC=BD
证明二:∵四边形ABCD是矩形
∴ ∠ABC=∠DCB=90°, AB=CD
而
∴ , ∴ AC=BD
A
图中还有哪些相等的线段?
证明:矩形的对角线相等.
图中我们常见的特殊三角形有哪些?
投圈游戏
问题: 体育节中有一投圈游戏,三个同学分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处,这样的队形对每个人公平吗 为什么?
B
C
D
A
O
直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半.
即兴练一练:
1.直角三角形两直角边分别为6和8,则其斜边上的中线长为________.
2.直角三角形两直角边分别为7和24,则其斜边上的中线长为________.
3.直角三角形两直角边分别为8和15,则其斜边上的中线长为________.
5
12.5
8.5
1.矩形具有而一般平行四边形不具有的性质是( ).
A、对角线相等 B、对边相等
C、对角相等 D、对角线互相平分
A
2.下面性质中,矩形不一定具有的是:( )
A、对角线相等 B、四个角都相等
C、是轴对称图形 D、对角线互相垂直
D
例1 如图,矩形ABCD的两条对角线交于点O, AB= 4cm ,∠AOD=120°, 求矩形对角线的长.
D
C
B
A
O
解矩形题时往往要注意:
1.矩形问题 三角形问题.
2.利用直角三角形的一些结论.
转化
1、矩形ABCD中,AC、BD相交于点O,AB=6,BC=8,则△ABO的周长为_____.
A
D
C
B
O
16
A
D
C
B
E
2、如图,矩形ABCD中,AE平分∠BAD交BC
于点E,ED=5cm,EC=3cm,求矩形的周长。
矩形问题
转 化
直角三角形问题
4、矩形问题 三角形问题.
3、直角三角形的一个重要性质:
直角三角形中,斜边上的中线等于斜边的一半.
1、矩形定义:
有一个角是直角的平行四边形叫矩形.
对边平行且相等
四个角均为直角
2、矩形
对角线互相平分且相等
转 化
3、(选做题)如图所示,锐角△ABC中,BE,CF是高,点M,N分别为BC,EF中点.求证:MN⊥EF.
1、(必做题)教材96面练习题:1、2题.
2、(必做题)如图,矩形ABCD的对角线交于点O,OF⊥BC,CE⊥BD, OF=4, OE∶BE=1∶3,求∠ADB 和 BD 的长.
