鲁教版(五四制)七年级下册数学 7.1二元一次方程组 教案
文档属性
| 名称 | 鲁教版(五四制)七年级下册数学 7.1二元一次方程组 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 785.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-17 17:13:58 | ||
图片预览


文档简介
课 题 7.1二元一次方程组 课 型 新授课
学习 目标 1、通过类比一元一次方程的知识,使学生认识二元一次方程、二元一次方程组及其解的概念
2、能用二元一次方程组刻画事物间的数量关系
3、渗透类比、建模的数学思想
学习 重点 二元一次方程、二元一次方程组及其解的意义
学习 难点 1、检验一对数是否是某个二元一次方程(组)的解
2、用二元一次方程组刻画事物间的数量关系
教学 方法 自主探究、合作交流
教学过程 课堂随记
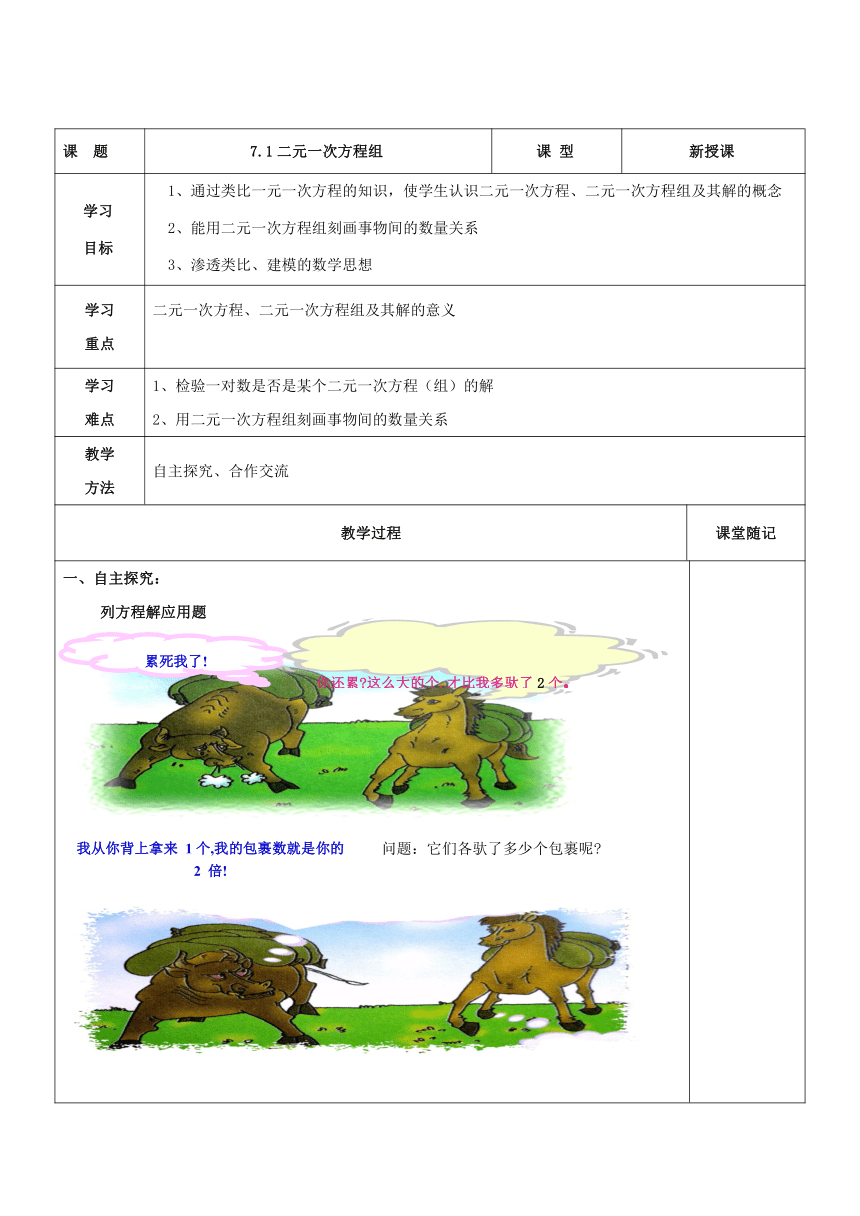
一、自主探究: 列方程解应用题
问题:它们各驮了多少个包裹呢?
课堂练习1:
1、下列是二元一次方程的有 .
① x+y+2z=6 ② 3x+2y ③ xy+4x-5y=9 ④ x=7y
⑤ 2x-5=3y ⑥ ⑦
2、若x?m-1+5y3n-2m = 7是二元一次方程,则m=______,n=_______。
3、已知、都是未知数,下列方程组是二元一次方程组的有
① ② ③ ④
二、互动交流
1、满足方程①的x,y的值有哪些?把它们填入表中
x
…
y
2、小组中加以展示,尝试总结方程①的解的情况
3、观察:满足方程①,且符合问题实际意义的x,y的值有哪些?与问题2相比较,你有何发现?
4、上表中哪对x,y的值还满足方程②?
课堂练习2:
1、已知的值:① ② ③ ④
(1)、是方程x-y=0的解有 ;
(2)、是方程2x+y=3的解有 ;
(3)、是二元一次方程组的解是 。
2、已知二元一次方程2x+y=3,用含x的代数式表示y,即y= 。
三、生成新知
1、方程中含有 个未知数,并且含有未知数的 的次数都是1的 方程,叫做二元一次方程。
2、方程组中有 个未知数,含有每个未知数的 的次数都是 ,并且一共有 个方程,这样的方程组叫做二元一次方程组。
3、使二元一次方程两边的值__________的两个未知数的_______,叫做二元一次方程的解。
4、二元一次方程组的两个方程的 ,叫做二元一次方程组的解。
四、当堂达标:
1.下列方程组中,不是二元一次方程组的是( )
A. B. C. D.
2.已知的值:①②③④其中,是二元一次方程的解的是( )
A.① B.② C.③ D.④
3.若方程有一解,则的值等于( )
A.1 B.2 C. D.
4、二元一次方程组的解是( )
A. B. C. D.
5、盒子里有5角和1元的硬币共10枚。其中5角的硬币有x枚,1元的有y枚,
(1)列出关于x,y的二元一次方程为 ;
(2)若5角的硬币比1元的硬币多2枚,列出关于x,y的二元一次方程为 ;
(3)若5角的硬币有6枚,则1元的硬币有 枚。
即 是二元一次方程组 的解。
五、课堂小结:通过本节课的学习,请分享你的收获
课堂随记
课堂随记
课堂随记
学习 目标 1、通过类比一元一次方程的知识,使学生认识二元一次方程、二元一次方程组及其解的概念
2、能用二元一次方程组刻画事物间的数量关系
3、渗透类比、建模的数学思想
学习 重点 二元一次方程、二元一次方程组及其解的意义
学习 难点 1、检验一对数是否是某个二元一次方程(组)的解
2、用二元一次方程组刻画事物间的数量关系
教学 方法 自主探究、合作交流
教学过程 课堂随记
一、自主探究: 列方程解应用题
问题:它们各驮了多少个包裹呢?
课堂练习1:
1、下列是二元一次方程的有 .
① x+y+2z=6 ② 3x+2y ③ xy+4x-5y=9 ④ x=7y
⑤ 2x-5=3y ⑥ ⑦
2、若x?m-1+5y3n-2m = 7是二元一次方程,则m=______,n=_______。
3、已知、都是未知数,下列方程组是二元一次方程组的有
① ② ③ ④
二、互动交流
1、满足方程①的x,y的值有哪些?把它们填入表中
x
…
y
2、小组中加以展示,尝试总结方程①的解的情况
3、观察:满足方程①,且符合问题实际意义的x,y的值有哪些?与问题2相比较,你有何发现?
4、上表中哪对x,y的值还满足方程②?
课堂练习2:
1、已知的值:① ② ③ ④
(1)、是方程x-y=0的解有 ;
(2)、是方程2x+y=3的解有 ;
(3)、是二元一次方程组的解是 。
2、已知二元一次方程2x+y=3,用含x的代数式表示y,即y= 。
三、生成新知
1、方程中含有 个未知数,并且含有未知数的 的次数都是1的 方程,叫做二元一次方程。
2、方程组中有 个未知数,含有每个未知数的 的次数都是 ,并且一共有 个方程,这样的方程组叫做二元一次方程组。
3、使二元一次方程两边的值__________的两个未知数的_______,叫做二元一次方程的解。
4、二元一次方程组的两个方程的 ,叫做二元一次方程组的解。
四、当堂达标:
1.下列方程组中,不是二元一次方程组的是( )
A. B. C. D.
2.已知的值:①②③④其中,是二元一次方程的解的是( )
A.① B.② C.③ D.④
3.若方程有一解,则的值等于( )
A.1 B.2 C. D.
4、二元一次方程组的解是( )
A. B. C. D.
5、盒子里有5角和1元的硬币共10枚。其中5角的硬币有x枚,1元的有y枚,
(1)列出关于x,y的二元一次方程为 ;
(2)若5角的硬币比1元的硬币多2枚,列出关于x,y的二元一次方程为 ;
(3)若5角的硬币有6枚,则1元的硬币有 枚。
即 是二元一次方程组 的解。
五、课堂小结:通过本节课的学习,请分享你的收获
课堂随记
课堂随记
课堂随记
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
