苏科版八年级下册数学 9.5三角形的中位线 课件(15张)
文档属性
| 名称 | 苏科版八年级下册数学 9.5三角形的中位线 课件(15张) | 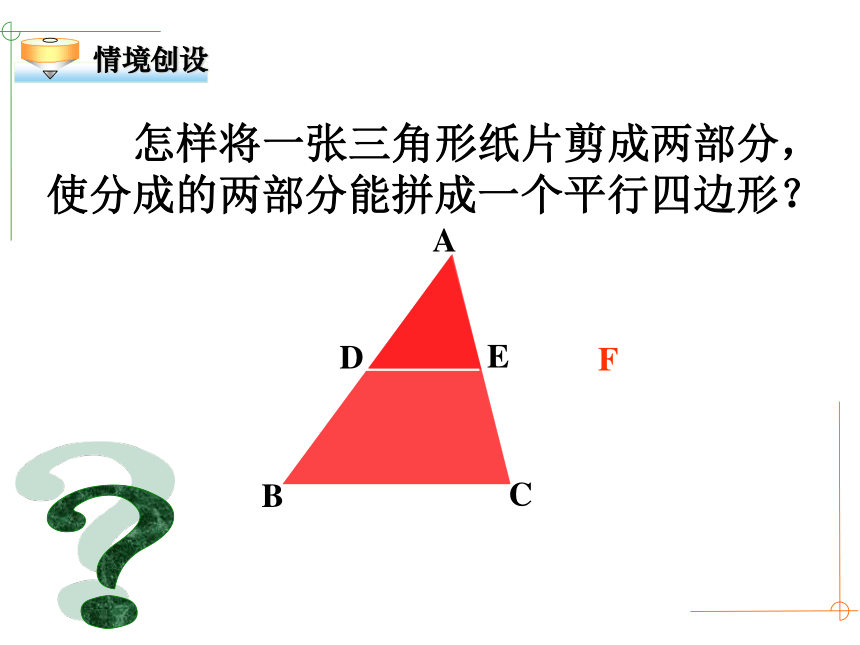 | |
| 格式 | ppt | ||
| 文件大小 | 476.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-18 11:25:23 | ||
图片预览


文档简介
怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形?
A
B
C
D
E
F
情境创设
C
B
A
F
E
D
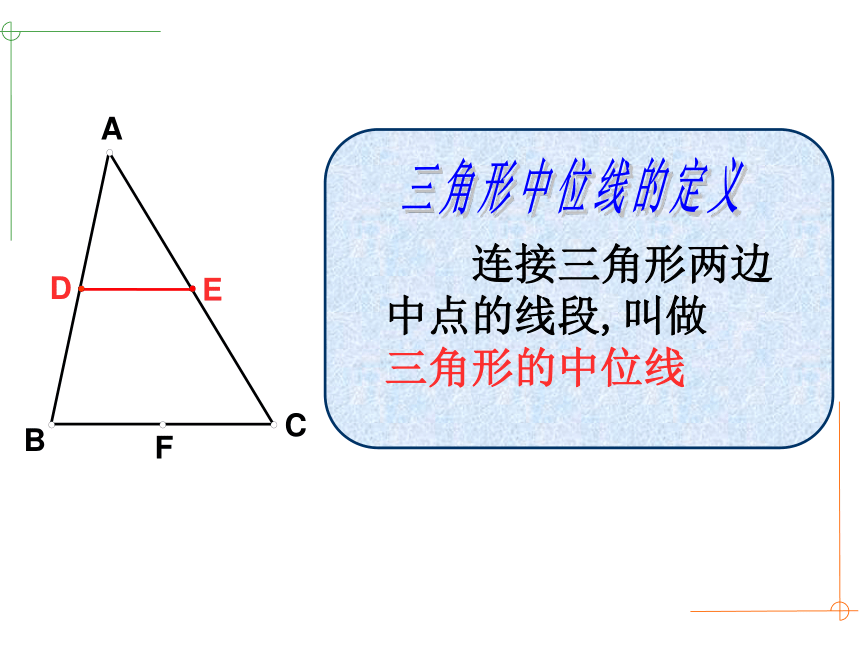
连接三角形两边中点的线段,叫做 三角形的中位线
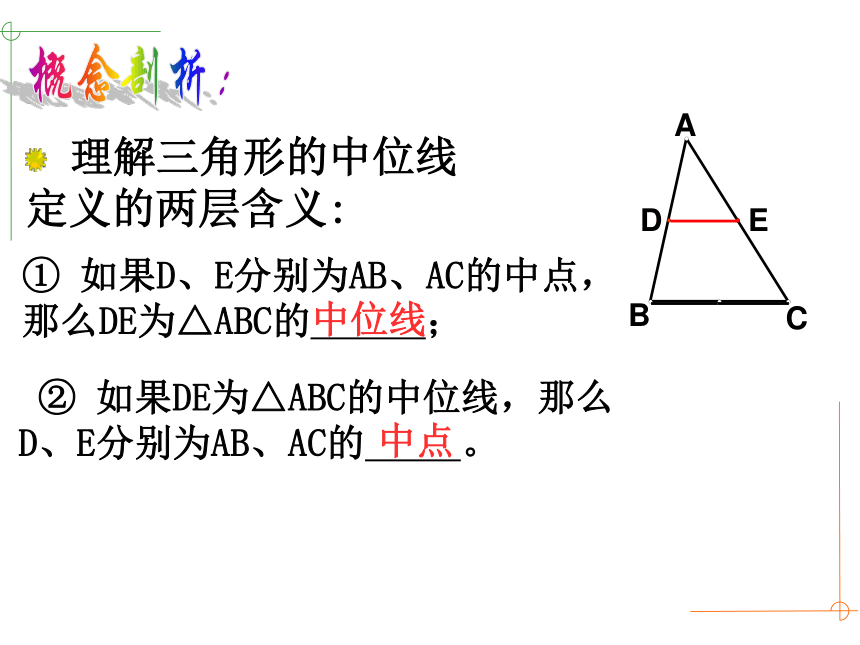
理解三角形的中位线定义的两层含义:
② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。
① 如果D、E分别为AB、AC的中点, 那么DE为△ABC的 ;
C
B
A
E
D
中位线
中点
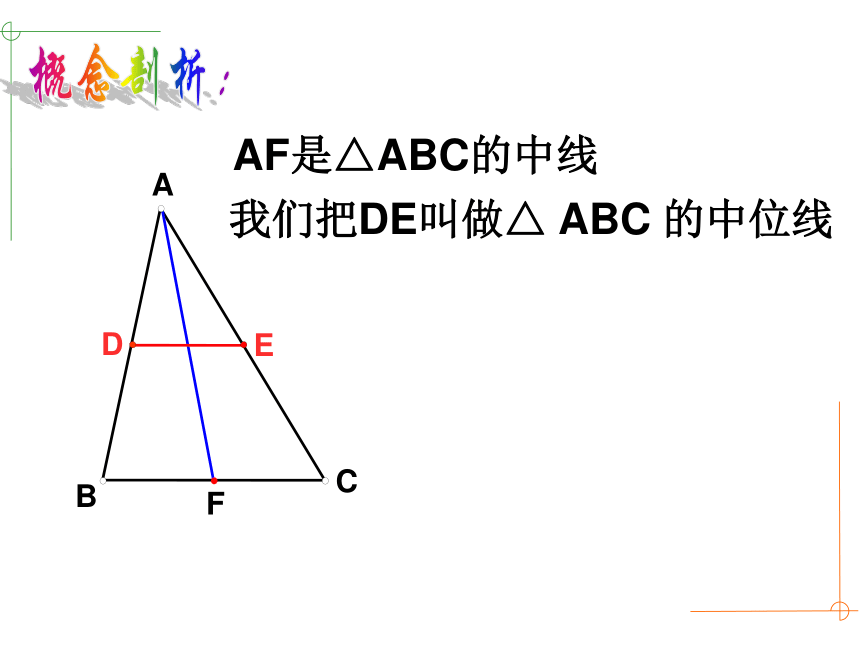
AF是△ABC的中线
我们把DE叫做△ ABC 的中位线
C
B
A
F
E
D
课题 §9.5
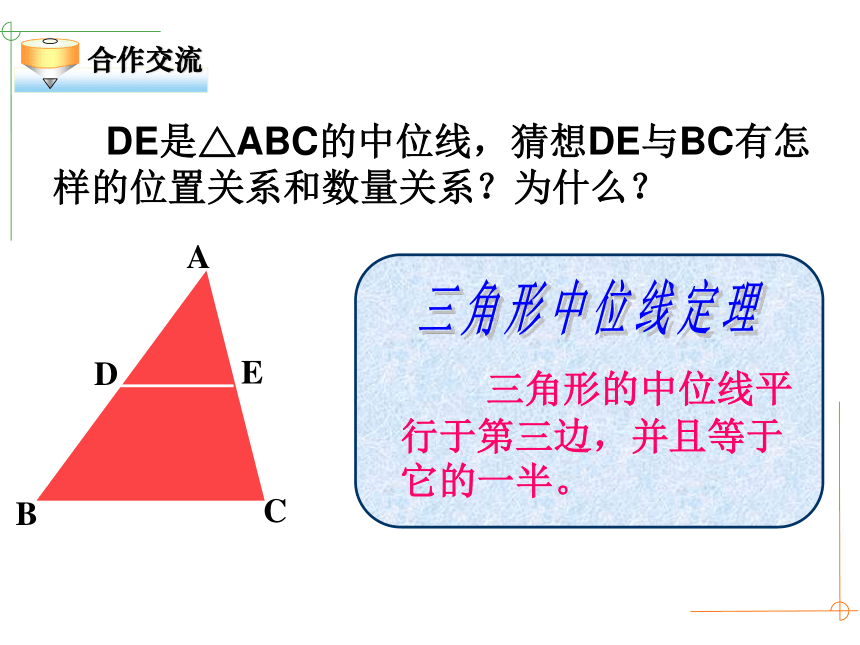
三角形的中位线平行于第三边,并且等于它的一半。
DE是△ABC的中位线,猜想DE与BC有怎样的位置关系和数量关系?为什么?
合作交流
B
A
C
D
E
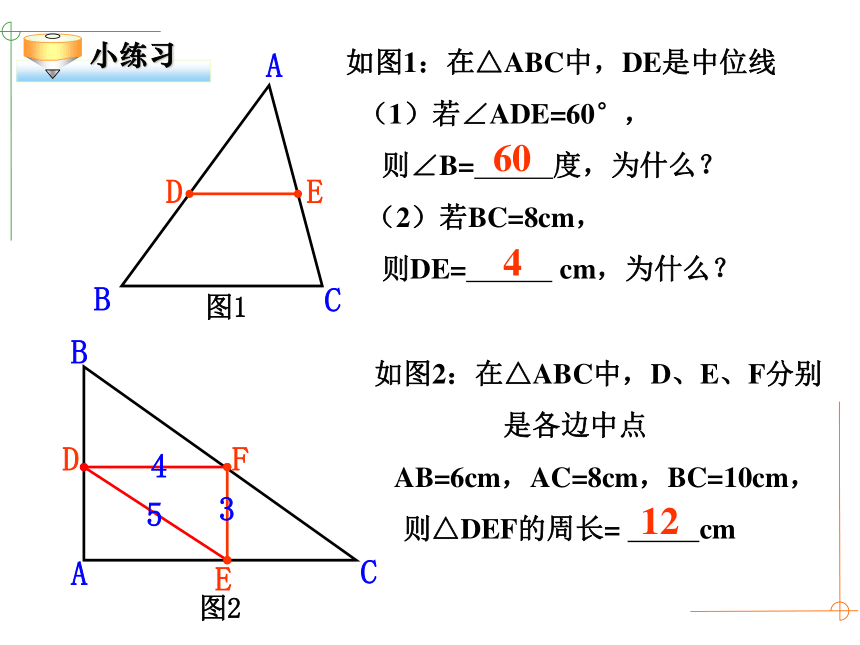
如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么?
如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm
图1
图2
60
4
12
A
B
C
D
E
B
A
C
D
E
F
5
4
3
小练习
例1. 在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,四边形EFGH是平行四边形吗?为什么?
A
C
B
E
D
H
F
G
解:四边形EFGH是平行四边形
∵E、F分别是AB、BC的中点
∴EF∥AC EF=1/2AC
理由:三角形的中位线平行于第三边,并且等于它的一半
同理:GH∥AC GH=1/2AC
∴EF∥GH且EF=GH
∴四边形EFGH是平行四边形
连结AC
理由:一组对边平行且相等的四边形是平行四边形
思考
A
C
B
E
D
H
F
G
如果AC=BD ,猜想四边形EFGH是什么图形?
如果AC⊥BD呢?
A
C
B
E
D
H
F
G
⑴顺次连接任意四边形四边中点所得的四边形是平行四边形
议一议:
顺次连接矩形的四边中点所得的四边形是什么形状?为什么?
如果将“矩形”改成“菱形”呢?
⑵顺次连接矩形的四边中点所得的四边形是菱形
⑶顺次连接菱形的四边中点所得的四边形是矩形
结论:
(1)
(2)
(3)
议一议:
1.如果顺次连接四边形四边中点所得的四边形是菱形,那么原四边形的两条对角线存在什么关系 ?
(两条对角线相等)
2.上问中的菱形改为矩形呢?
(两条对角线互相垂直)
3.当四边形满足什么条件时,顺次连接它的四边中点 所得的四边形是正方形?
(两条对角线互相垂直且相等)
④顺次连结对角线相等且互相垂直的四边形四边中点所得的四边形是—————
②顺次连结对角线相等的四边形四边中点所得的四边形是————
③顺次连结对角线互相垂直的四边形四边中点所得的四边形是————
①顺次连结四边形四边中点所得的四边形是——————
平行四边形.
矩形.
菱形.
正方形.
1、如图,D、E、F分别是△ABC各边的中点
(1)如果EF=4cm,那么BC=
___cm,
如果AB=10cm,那么DF=___cm
(2)中线AD与中位线EF的关系是_______
A
B
C
D
E
F
4
例2、已知△ABC中,∠B=2∠C,AD⊥BC于D,M为BC中点,求证:DM= AB
A
B
D
C
M
N
A
B
C
D
E
F
情境创设
C
B
A
F
E
D
连接三角形两边中点的线段,叫做 三角形的中位线
理解三角形的中位线定义的两层含义:
② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。
① 如果D、E分别为AB、AC的中点, 那么DE为△ABC的 ;
C
B
A
E
D
中位线
中点
AF是△ABC的中线
我们把DE叫做△ ABC 的中位线
C
B
A
F
E
D
课题 §9.5
三角形的中位线平行于第三边,并且等于它的一半。
DE是△ABC的中位线,猜想DE与BC有怎样的位置关系和数量关系?为什么?
合作交流
B
A
C
D
E
如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么?
如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm
图1
图2
60
4
12
A
B
C
D
E
B
A
C
D
E
F
5
4
3
小练习
例1. 在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,四边形EFGH是平行四边形吗?为什么?
A
C
B
E
D
H
F
G
解:四边形EFGH是平行四边形
∵E、F分别是AB、BC的中点
∴EF∥AC EF=1/2AC
理由:三角形的中位线平行于第三边,并且等于它的一半
同理:GH∥AC GH=1/2AC
∴EF∥GH且EF=GH
∴四边形EFGH是平行四边形
连结AC
理由:一组对边平行且相等的四边形是平行四边形
思考
A
C
B
E
D
H
F
G
如果AC=BD ,猜想四边形EFGH是什么图形?
如果AC⊥BD呢?
A
C
B
E
D
H
F
G
⑴顺次连接任意四边形四边中点所得的四边形是平行四边形
议一议:
顺次连接矩形的四边中点所得的四边形是什么形状?为什么?
如果将“矩形”改成“菱形”呢?
⑵顺次连接矩形的四边中点所得的四边形是菱形
⑶顺次连接菱形的四边中点所得的四边形是矩形
结论:
(1)
(2)
(3)
议一议:
1.如果顺次连接四边形四边中点所得的四边形是菱形,那么原四边形的两条对角线存在什么关系 ?
(两条对角线相等)
2.上问中的菱形改为矩形呢?
(两条对角线互相垂直)
3.当四边形满足什么条件时,顺次连接它的四边中点 所得的四边形是正方形?
(两条对角线互相垂直且相等)
④顺次连结对角线相等且互相垂直的四边形四边中点所得的四边形是—————
②顺次连结对角线相等的四边形四边中点所得的四边形是————
③顺次连结对角线互相垂直的四边形四边中点所得的四边形是————
①顺次连结四边形四边中点所得的四边形是——————
平行四边形.
矩形.
菱形.
正方形.
1、如图,D、E、F分别是△ABC各边的中点
(1)如果EF=4cm,那么BC=
___cm,
如果AB=10cm,那么DF=___cm
(2)中线AD与中位线EF的关系是_______
A
B
C
D
E
F
4
例2、已知△ABC中,∠B=2∠C,AD⊥BC于D,M为BC中点,求证:DM= AB
A
B
D
C
M
N
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
