绝对值不等式解法
图片预览


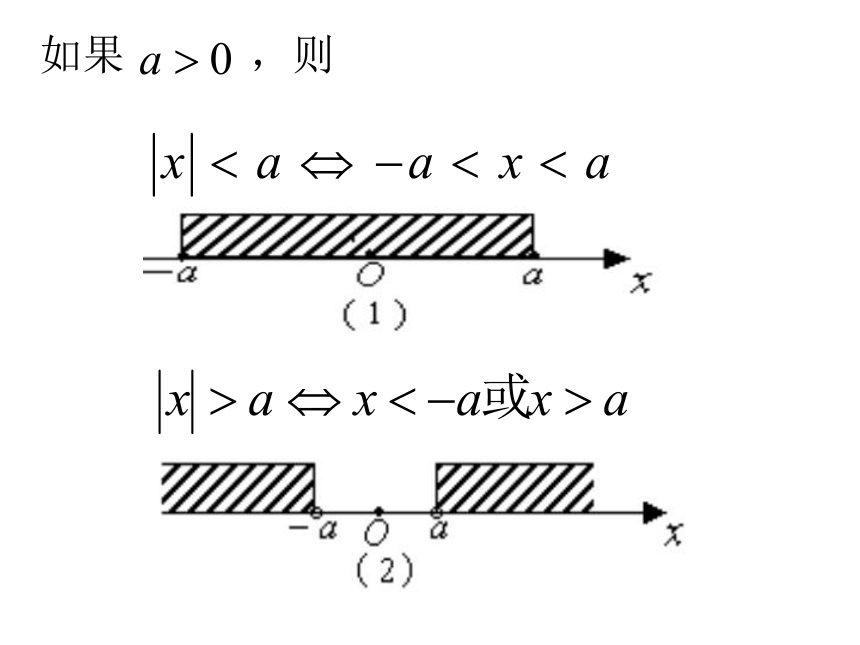



文档简介
(共15张PPT)
绝对值不等式的解法
复习:
x=0
|x|=
x>0
x
0
x<0
- x
1.绝对值的意义:
2.几何意义:
x1
|x1|
|x2|
=|OA|
=|OB|
一个数的绝对值表示这个数对应的点到
原点的距离.
x
x2
A
B
A
O
类比求:|x|<3的解集
|x|>3 的解集
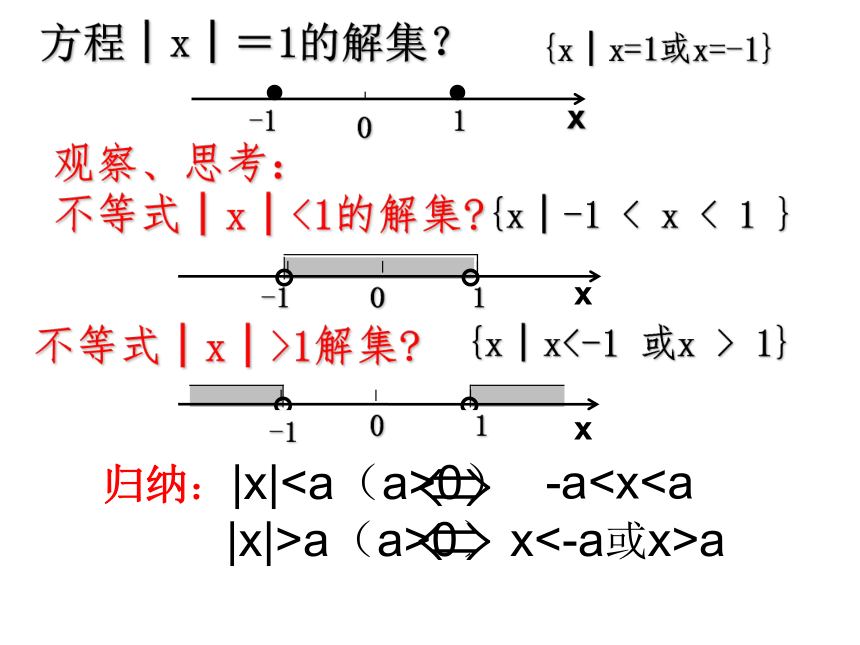
观察、思考:
不等式│x│<1的解集
方程│x│=1的解集?
{x│x=1或x=-1}
{x│-1 < x < 1 }
不等式│x│>1解集
{x│x<-1 或x > 1}
归纳:|x|0)
|x|>a(a>0)
-ax<-a或x>a
1
-1
0
x
x
0
1
-1
-1
1
0
x
如果
,则
试求: |x|<-2的解集
|x|>-2的解集
如果
,则
如果把|x|<1中的x换成“3x-1”,也就是
| 3x-1 | <1如何解?
引伸:
解题反思:
如果把|x|>1中的x换成“3x-1”,也就是
| 3x-1 | >1如何解?
整体换元。
不等式的解法:
例1 解不等式
例2 解不等式
型如:
例 1 解不等式
解:
解得
因此,原不等式的解集为
得
由
2
1
3
-
x
它的解集是数轴上到坐标为
的点的距离不大于
的点的集合.
可以化为:
的解的几何意义:
不等式
2
1
3
-
x
1
0
x
解:
所以
从而
所以原不等式的解集为
例 2 解不等式
.
7
3
-
2
x
得
由
不等式的解法:
型如
巩固练习
求下列不等式的解集
课堂小结
1.绝对值的意义
2.几何意义
3.归纳:
4.归纳:
数学思想:
数形结合的思想
整体的思想
课堂小结
作业
课本P20 6、7.
绝对值不等式的解法
复习:
x=0
|x|=
x>0
x
0
x<0
- x
1.绝对值的意义:
2.几何意义:
x1
|x1|
|x2|
=|OA|
=|OB|
一个数的绝对值表示这个数对应的点到
原点的距离.
x
x2
A
B
A
O
类比求:|x|<3的解集
|x|>3 的解集
观察、思考:
不等式│x│<1的解集
方程│x│=1的解集?
{x│x=1或x=-1}
{x│-1 < x < 1 }
不等式│x│>1解集
{x│x<-1 或x > 1}
归纳:|x|
|x|>a(a>0)
-a
1
-1
0
x
x
0
1
-1
-1
1
0
x
如果
,则
试求: |x|<-2的解集
|x|>-2的解集
如果
,则
如果把|x|<1中的x换成“3x-1”,也就是
| 3x-1 | <1如何解?
引伸:
解题反思:
如果把|x|>1中的x换成“3x-1”,也就是
| 3x-1 | >1如何解?
整体换元。
不等式的解法:
例1 解不等式
例2 解不等式
型如:
例 1 解不等式
解:
解得
因此,原不等式的解集为
得
由
2
1
3
-
x
它的解集是数轴上到坐标为
的点的距离不大于
的点的集合.
可以化为:
的解的几何意义:
不等式
2
1
3
-
x
1
0
x
解:
所以
从而
所以原不等式的解集为
例 2 解不等式
.
7
3
-
2
x
得
由
不等式的解法:
型如
巩固练习
求下列不等式的解集
课堂小结
1.绝对值的意义
2.几何意义
3.归纳:
4.归纳:
数学思想:
数形结合的思想
整体的思想
课堂小结
作业
课本P20 6、7.
