三角函数模型简单应用
图片预览




文档简介
(共17张PPT)
三角函数模型的简单应用
--- 货船进出港问题
高一(24)班 范琴
我们已经学习了三角函数的概念、图象与性质,其中周期性是三角函数的一个显著性质.在现实生活中,如果某种变化着的现象具有周期性,那么它就可以借助三角函数来描述,并利用三角函数的图象和性质解决相应的实际问题.
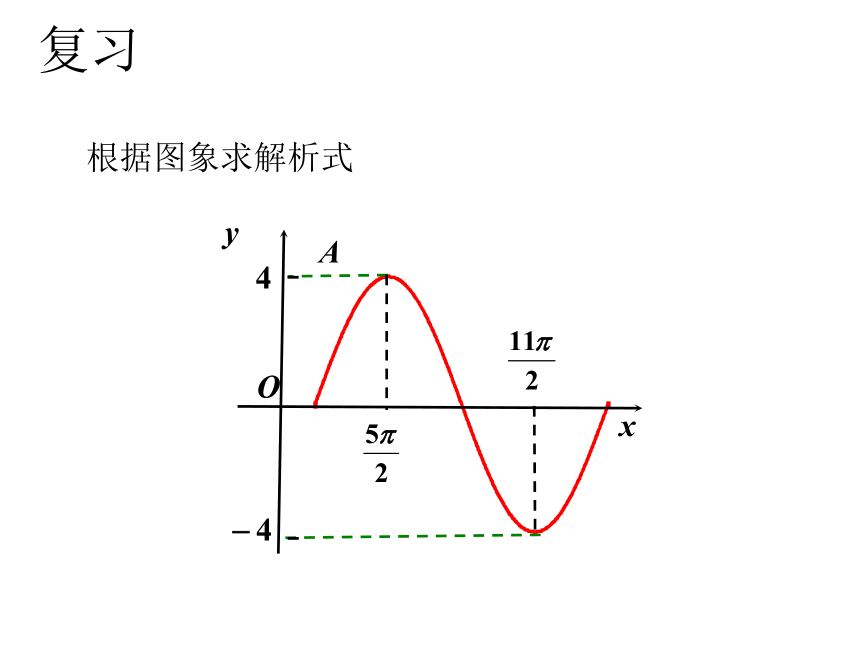
复习
根据图象求解析式
根据相关数据进行三角函数拟合
【背景材料】 海水受日月的引力,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表:
5.0
2.5
5.0
7.5
5.0
2.5
5.0
7.5
5.0
水深/米
24
21
18
15
12
9
6
3
0
时刻
观察表格中的数据,每天水深的变化具有什么特点?
呈周期性变化规律.
水深最大值为7.5
最小值为2.5.
5.0
2.5
5.0
7.5
5.0
2.5
5.0
7.5
5.0
水深/米
24
21
18
15
12
9
6
3
0
时刻
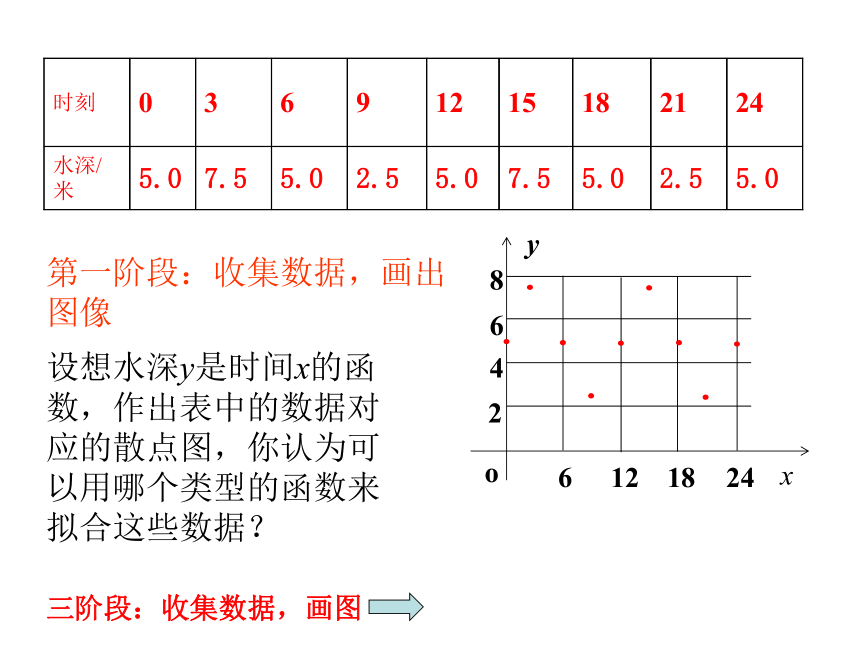
设想水深y是时间x的函数,作出表中的数据对应的散点图,你认为可以用哪个类型的函数来拟合这些数据?
y
o
18
24
6
12
2
4
6
8
x
5.0
2.5
5.0
7.5
5.0
2.5
5.0
7.5
5.0
水深/米
24
21
18
15
12
9
6
3
0
时刻
第一阶段:收集数据,画出图像
三阶段:收集数据,画图
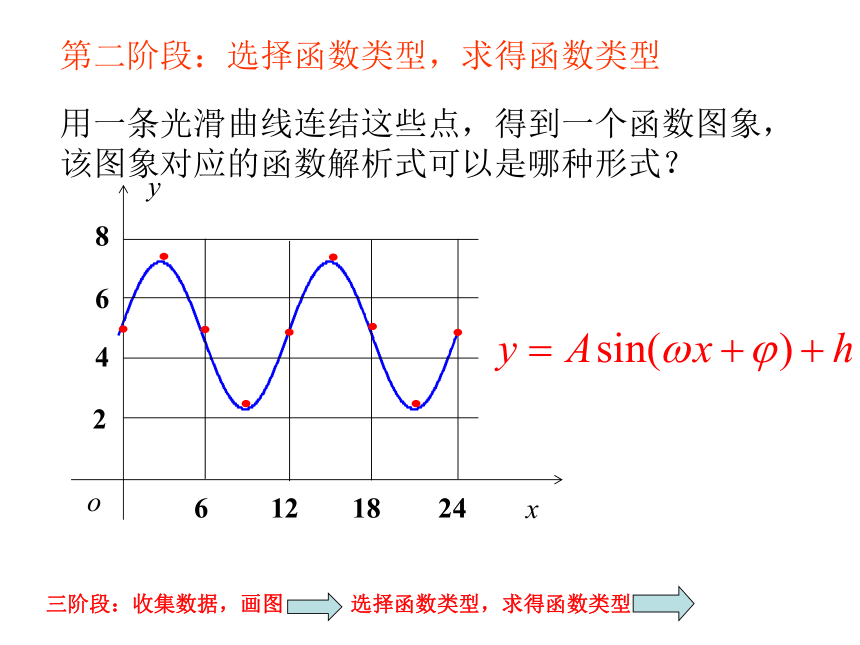
用一条光滑曲线连结这些点,得到一个函数图象,该图象对应的函数解析式可以是哪种形式?
x
y
o
18
24
6
12
2
4
6
8
第二阶段:选择函数类型,求得函数类型
三阶段:收集数据,画图
选择函数类型,求得函数类型
用函数 来刻画水深和时间之间的对应关系,如何确定解析式中的参数值?
x
y
o
18
24
6
12
2
4
6
8
最大值7.5
最小值2.5
三阶段:收集数据,画图
选择函数类型,求得函数类型
⑴这个港口的水深与时间的关系可
用函数 近似描述,你能根据这个函数模型,求出各整点时水深的近似值吗?(精确到0.001)
第三阶段:将函数模型应用于实际问题
三阶段:收集数据,画图
选择函数类型,求得函数类型
应用于实际
3.754
2.835
2.500
2.835
3.754
5.000
水深
23:00
22:00
21:00
20:00
19:00
18:00
时刻
6.250
7.165
7.500
7.165
6.250
5.000
水深
17:00
16:00
15:00
14:00
13:00
12:00
时刻
3.754
2.835
2.500
2.835
3.754
5.000
水深
11:00
10:00
9:00
8:00
7:00
6:00
时刻
6.250
7.165
7.500
7.165
6.250
5.000
水深
5:00
4:00
3:00
2:00
1:00
0:00
时刻
三阶段:收集数据,画图
选择函数类型,求得函数类型
应用于实际
(2)一条货船的吃水深度(船底与水面的距离)为4米,安全例规定至少要有1.5米的安全间隙 (船底与海洋底的距离),该船何时能进入港口 在港口能呆多久
A
B
C
D
o
x
y
2
4
6
8
5
10
15
y=5.5
三阶段:收集数据,画图
选择函数类型,求得函数类型
应用于实际
由计算器可得
SHIFT
sin-1
MODE
MODE
2
0.2
=
0.20135792≈0.2014
货船需要的安全水深为4+1.5=5.5(米),所以当y≥5.5时就可以进港 .
三阶段:收集数据,画图
选择函数类型,求得函数类型
应用于实际
y
O
x
5
10
15
2
4
6
8
A
B
C
D
y=5.5
因此,货船可以在0时30分左右进港,早晨5时30分左右出港;或在中午12时30分左右进港,下午17时30分左右出港.每次可以在港口停留5小时左右.
三阶段:收集数据,画图
选择函数类型,求得函数类型
应用于实际
思考
(3)若某船的吃水深度为4米.安全间隙为1.5米,该船在2:00开始卸货,吃水深度以每小时0.3米的速度减少,那么该船在什么时间必须停止卸货,将船驶向较深的水域
三阶段:收集数据,画图
选择函数类型,求得函数类型
应用于实际
在一个港口,相邻两次高潮发生时间相距12h,低潮时水的深度为8.4m,高潮时为16m,一次高潮发生在4:00.每天涨潮落潮时,水的深度y(m)与时间t(h)近似满足关系式
(1)若从0:00开始计算时间,选用一个三角函数来 近似描述该港口的水深y和t之间的函数关系
(2)17:00该港口的水深为多少?(保留一位有效数字)
(3)这一天有多少小时水深低于10.3m?
1、物理情景——
①简谐运动
②星体的环绕运动
2、地理情景——
①气温变化规律
②月圆与月缺
3、心理、生理现象——
①情绪的波动
②智力变化状况
③体力变化状况
4、日常生活现象——
①涨潮与退潮
②股票变化
…………
三角函数模型在生活中的其他应用举例
对于现实世界中具有周期现象的实际问题,可以利用三角函数模型描述其变化规律.可分为三阶段:第一阶段:收集数据,画图;第二阶段:选择函数类型,并求得函数类型;第三阶段:将函数模型应用的实际中
小结:
三角函数模型的简单应用
--- 货船进出港问题
高一(24)班 范琴
我们已经学习了三角函数的概念、图象与性质,其中周期性是三角函数的一个显著性质.在现实生活中,如果某种变化着的现象具有周期性,那么它就可以借助三角函数来描述,并利用三角函数的图象和性质解决相应的实际问题.
复习
根据图象求解析式
根据相关数据进行三角函数拟合
【背景材料】 海水受日月的引力,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表:
5.0
2.5
5.0
7.5
5.0
2.5
5.0
7.5
5.0
水深/米
24
21
18
15
12
9
6
3
0
时刻
观察表格中的数据,每天水深的变化具有什么特点?
呈周期性变化规律.
水深最大值为7.5
最小值为2.5.
5.0
2.5
5.0
7.5
5.0
2.5
5.0
7.5
5.0
水深/米
24
21
18
15
12
9
6
3
0
时刻
设想水深y是时间x的函数,作出表中的数据对应的散点图,你认为可以用哪个类型的函数来拟合这些数据?
y
o
18
24
6
12
2
4
6
8
x
5.0
2.5
5.0
7.5
5.0
2.5
5.0
7.5
5.0
水深/米
24
21
18
15
12
9
6
3
0
时刻
第一阶段:收集数据,画出图像
三阶段:收集数据,画图
用一条光滑曲线连结这些点,得到一个函数图象,该图象对应的函数解析式可以是哪种形式?
x
y
o
18
24
6
12
2
4
6
8
第二阶段:选择函数类型,求得函数类型
三阶段:收集数据,画图
选择函数类型,求得函数类型
用函数 来刻画水深和时间之间的对应关系,如何确定解析式中的参数值?
x
y
o
18
24
6
12
2
4
6
8
最大值7.5
最小值2.5
三阶段:收集数据,画图
选择函数类型,求得函数类型
⑴这个港口的水深与时间的关系可
用函数 近似描述,你能根据这个函数模型,求出各整点时水深的近似值吗?(精确到0.001)
第三阶段:将函数模型应用于实际问题
三阶段:收集数据,画图
选择函数类型,求得函数类型
应用于实际
3.754
2.835
2.500
2.835
3.754
5.000
水深
23:00
22:00
21:00
20:00
19:00
18:00
时刻
6.250
7.165
7.500
7.165
6.250
5.000
水深
17:00
16:00
15:00
14:00
13:00
12:00
时刻
3.754
2.835
2.500
2.835
3.754
5.000
水深
11:00
10:00
9:00
8:00
7:00
6:00
时刻
6.250
7.165
7.500
7.165
6.250
5.000
水深
5:00
4:00
3:00
2:00
1:00
0:00
时刻
三阶段:收集数据,画图
选择函数类型,求得函数类型
应用于实际
(2)一条货船的吃水深度(船底与水面的距离)为4米,安全例规定至少要有1.5米的安全间隙 (船底与海洋底的距离),该船何时能进入港口 在港口能呆多久
A
B
C
D
o
x
y
2
4
6
8
5
10
15
y=5.5
三阶段:收集数据,画图
选择函数类型,求得函数类型
应用于实际
由计算器可得
SHIFT
sin-1
MODE
MODE
2
0.2
=
0.20135792≈0.2014
货船需要的安全水深为4+1.5=5.5(米),所以当y≥5.5时就可以进港 .
三阶段:收集数据,画图
选择函数类型,求得函数类型
应用于实际
y
O
x
5
10
15
2
4
6
8
A
B
C
D
y=5.5
因此,货船可以在0时30分左右进港,早晨5时30分左右出港;或在中午12时30分左右进港,下午17时30分左右出港.每次可以在港口停留5小时左右.
三阶段:收集数据,画图
选择函数类型,求得函数类型
应用于实际
思考
(3)若某船的吃水深度为4米.安全间隙为1.5米,该船在2:00开始卸货,吃水深度以每小时0.3米的速度减少,那么该船在什么时间必须停止卸货,将船驶向较深的水域
三阶段:收集数据,画图
选择函数类型,求得函数类型
应用于实际
在一个港口,相邻两次高潮发生时间相距12h,低潮时水的深度为8.4m,高潮时为16m,一次高潮发生在4:00.每天涨潮落潮时,水的深度y(m)与时间t(h)近似满足关系式
(1)若从0:00开始计算时间,选用一个三角函数来 近似描述该港口的水深y和t之间的函数关系
(2)17:00该港口的水深为多少?(保留一位有效数字)
(3)这一天有多少小时水深低于10.3m?
1、物理情景——
①简谐运动
②星体的环绕运动
2、地理情景——
①气温变化规律
②月圆与月缺
3、心理、生理现象——
①情绪的波动
②智力变化状况
③体力变化状况
4、日常生活现象——
①涨潮与退潮
②股票变化
…………
三角函数模型在生活中的其他应用举例
对于现实世界中具有周期现象的实际问题,可以利用三角函数模型描述其变化规律.可分为三阶段:第一阶段:收集数据,画图;第二阶段:选择函数类型,并求得函数类型;第三阶段:将函数模型应用的实际中
小结:
