2020-2021学年人教版八年级下册数学第18章《平行四边形》(四)(Word版 含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学第18章《平行四边形》(四)(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 402.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-18 11:28:41 | ||
图片预览


文档简介
第18章
《平行四边形》单元测试
一.选择题(每题3分,共30分)
1.如图,在菱形ABCD中,∠B=60°,AB=4,则以AC为一边的正方形ACEF的周长为( )
A.14
B.15
C.16
D.17
2.
如图,在矩形ABCD中,对角线AC,BD相交于点O,过O的直线EF分别交AB,CD于点E,F,若图中阴影部分的面积为6,则矩形ABCD的面积为( )
A.12
B.18
C.24
D.30
3.
平行四边形ABCD的对角线交于点O,有五个条件:①AC=BD,②∠ABC=90°,③AB=AC,④AB=BC,⑤AC⊥BD,则下列哪个组合可判定这个四边形是正方形?( )
A.①②
B.①③
C.①④
D.④⑤
4.如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=( )
A.90°α
B.90°+
α
C.
α
D.360°α
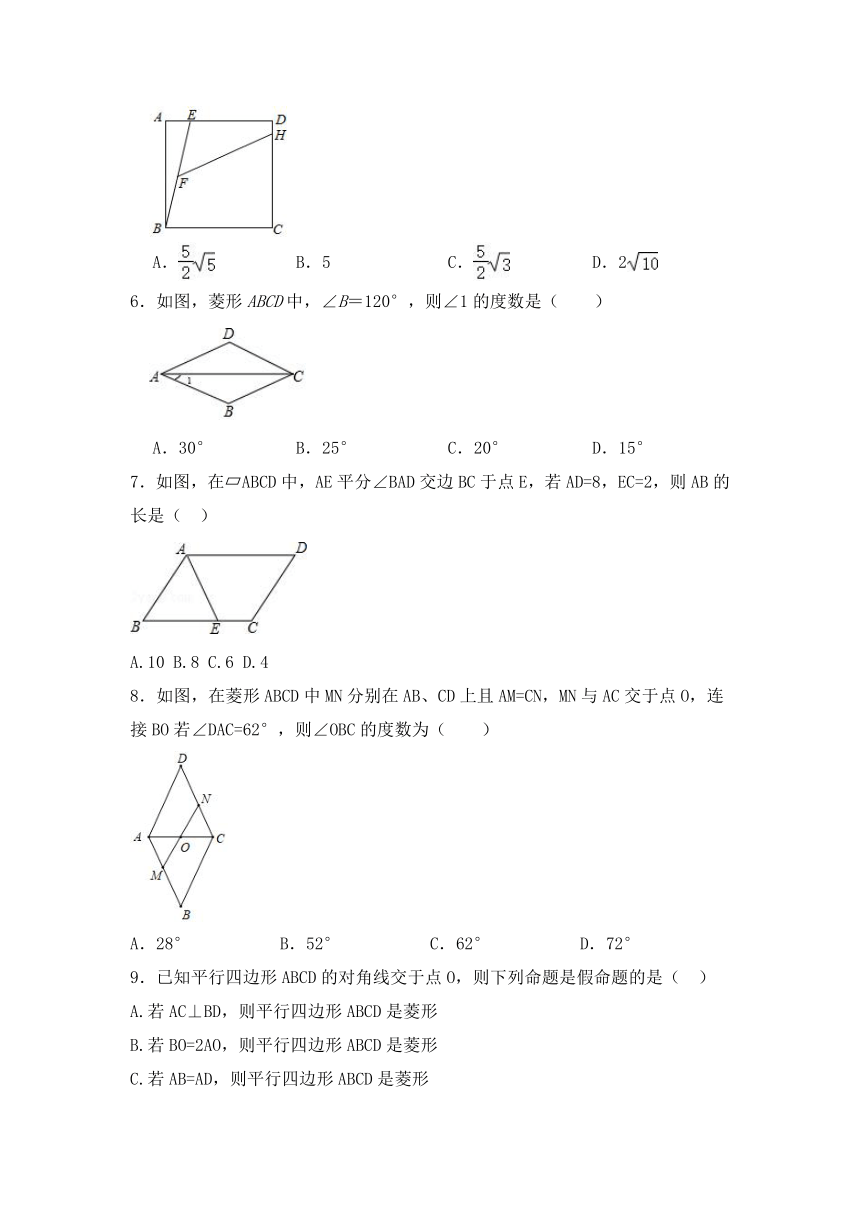
5.如图,正方形ABCD中,DE=2AE=4,F是BE的中点,点H在CD上,∠EFH=45°,则FH的长度为( )
A.
B.5
C.
D.2
6.如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30°
B.25°
C.20°
D.15°
7.如图,在?ABCD中,AE平分∠BAD交边BC于点E,若AD=8,EC=2,则AB的长是(
)
A.10
B.8
C.6
D.4
8.如图,在菱形ABCD中MN分别在AB、CD上且AM=CN,MN与AC交于点O,连接BO若∠DAC=62°,则∠OBC的度数为( )
A.28°
B.52°
C.62°
D.72°
9.已知平行四边形ABCD的对角线交于点O,则下列命题是假命题的是(
)
A.若AC⊥BD,则平行四边形ABCD是菱形
B.若BO=2AO,则平行四边形ABCD是菱形
C.若AB=AD,则平行四边形ABCD是菱形
D.若∠ABD=∠CBD,则平行四边形ABCD是菱形
10.如图,若要使?ABCD成为菱形,则可添加的条件是(
)
A.AB=CD
B.AD=BC
C.AB=BC
D.AC=BD
二.填空题(每题4分,共20分)
11.如图,□ABCD中,E是BA的中点,连接DE,将△DAE沿DE折叠,使点A落在□ABCD内部的点F处.若∠CBF=25°,则∠FDA的度数为_________.
12.
若以A(-0.5,0),B(2,0),C(0,1)三点为顶点画平行四边形,则第四个顶点不可能在第________象限.
13.如图,矩形ABCD中,E是BC的中点,矩形ABCD的周长是20
cm,AE=5
cm,则AB的长为________
cm.
14.如图①,矩形纸片ABCD中,AB=5,BC=3,先按图②操作:将矩形纸片ABCD沿过点A的直线折叠,使点D落在边AB上的点E处,折痕为AF再按图③操作:沿过点F的直线折叠,使点C落在EF上的点H处,折痕为FG,则A,H两点间
的距离为_________.
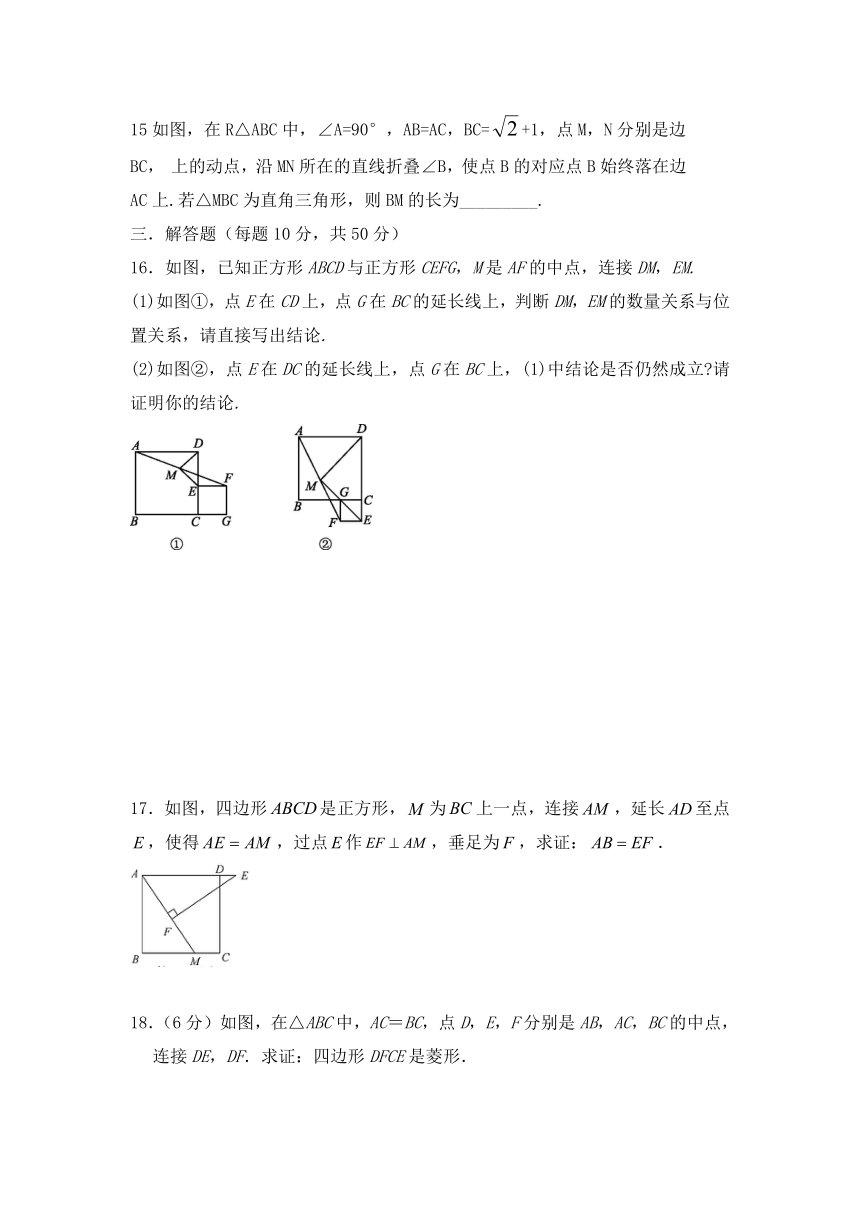
15如图,在R△ABC中,∠A=90°,AB=AC,BC=+1,点M,N分别是边BC,
上的动点,沿MN所在的直线折叠∠B,使点B的对应点B始终落在边AC上.若△MBC为直角三角形,则BM的长为_________.
三.解答题(每题10分,共50分)
16.如图,已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图①,点E在CD上,点G在BC的延长线上,判断DM,EM的数量关系与位置关系,请直接写出结论.
(2)如图②,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论.
17.如图,四边形是正方形,为上一点,连接,延长至点,使得,过点作,垂足为,求证:.
18.(6分)如图,在△ABC中,AC=BC,点D,E,F分别是AB,AC,BC的中点,连接DE,DF.求证:四边形DFCE是菱形.
19.
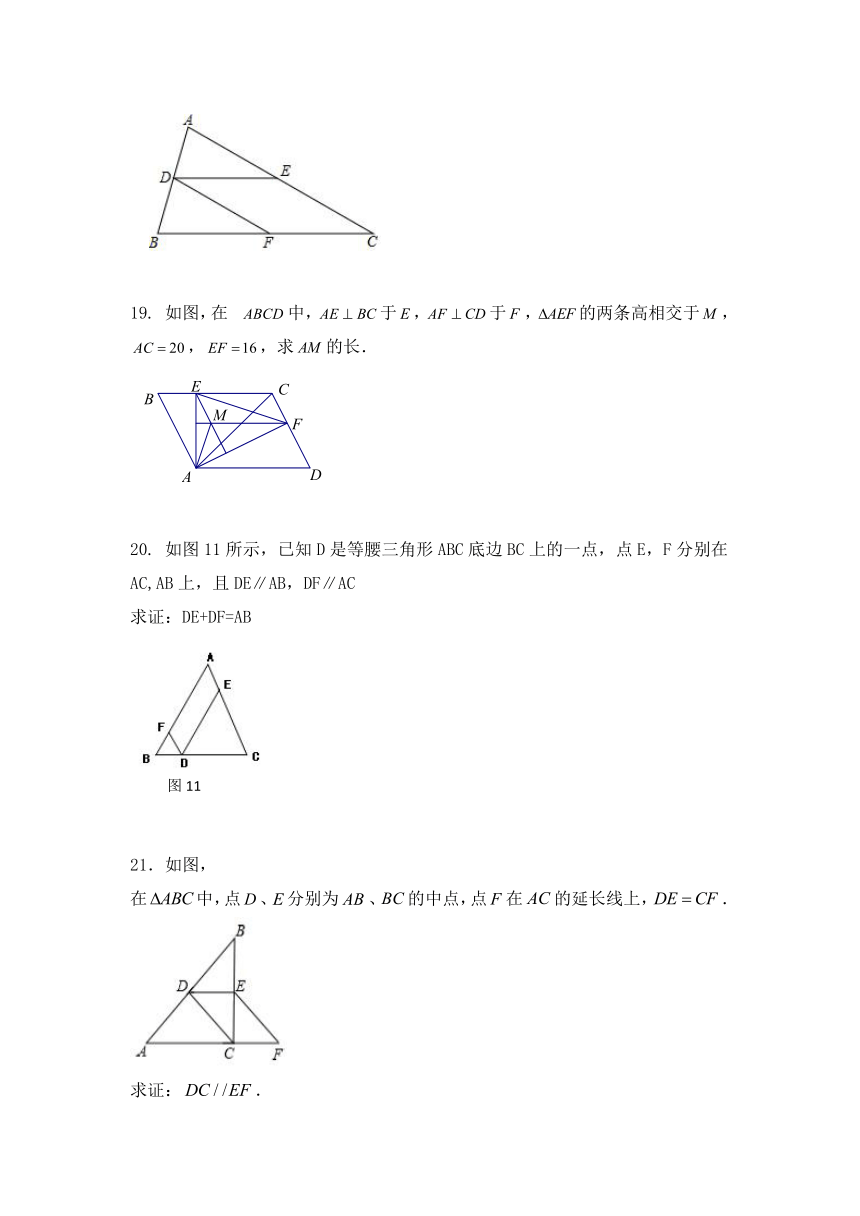
如图,在中,于,于,的两条高相交于,,,求的长.
20.
如图11所示,已知D是等腰三角形ABC底边BC上的一点,点E,F分别在AC,AB上,且DE∥AB,DF∥AC
求证:DE+DF=AB
21.如图,
在中,点、分别为、的中点,点在的延长线上,.
求证:.
22.如图,在?ABCD中,AF平分∠BAD交BC于点F,CE平分∠BCD交AD于点E.
(1)若AD=12,AB=8,求CF的长;
(2)连接BE和AF相交于点G,DF和CE相交于点H,求证:EF和GH互相平分.
23.平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.
(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;
(2)如果四边形ABCD是正方形,四边形OBEC也是正方形吗?如果是,请给予证明;如果不是,请说明理由.
24.已知,如图,在?ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形:
(2)若菱形ABEF的周长为16,∠BEF=120°,求AE的大小.
参考答案
一.选择题
1.D
2.B
3.C
4.
C.
5.
D.
6.
C.
7.
C.
8.A.
9.
B.10.C
二.填空题(共5小题)
11.
(-3,2).
12.三
13.4
14.
【答案】∠BAD=90°(答案不唯一) 【解析】∵?ABCD的对角线AC与BD相交于点O,且AC⊥BD,∴?ABCD是菱形,当∠BAD=90°时,菱形ABCD为正方形.故可添加条件:∠BAD=90°.
15.
12.5
三.解答题(共5小题)
16.解:(1)结论:DM⊥EM,DM=EM.
[解析]延长EM交AD于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,
AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME.
(2)结论不变.DM⊥EM,DM=EM.
证明:延长EM交DA的延长线于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,
AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,
∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME.
17.证明:四边形为正方形,
,,
,
,
,
在和中,,
,
.
18.证明:∵点D,E,F分别是AB,AC,BC的中点,
∴DE∥CF,DE=BC,DF∥CE,DF=AC,
∴四边形DECF是平行四边形,
∵AC=BC,
∴DE=DF,
∴四边形DFCE是菱形;
19.
【答案】
20.证明:∵DE∥AB,DF∥AC
∴四边形AEDF是平行四边形,∴DF=AE,又∵DE∥AB,∴∠B=∠EDC,又∵AB=AC,∴∠B=∠C,∴∠C=∠EDC,∴DE=CE,∴DF+DE=AE+CE=AC=AB.
21.∵在中,点、分别为、的中点
∴是的中位线
∴
即
∵
∴四边形为平行四边形
∴.
参考答案
一.选择题
1.D
2.B
3.C
4.
C.
5.
D.
6.
C.
7.
C.
8.A.
9.
B.10.C
二.填空题(共5小题)
11.
(-3,2).
12.三
13.4
14.
【答案】∠BAD=90°(答案不唯一) 【解析】∵?ABCD的对角线AC与BD相交于点O,且AC⊥BD,∴?ABCD是菱形,当∠BAD=90°时,菱形ABCD为正方形.故可添加条件:∠BAD=90°.
15.
12.5
三.解答题(共5小题)
16.解:(1)结论:DM⊥EM,DM=EM.
[解析]延长EM交AD于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,
AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME.
(2)结论不变.DM⊥EM,DM=EM.
证明:延长EM交DA的延长线于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,
AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,
∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME.
17.证明:四边形为正方形,
,,
,
,
,
在和中,,
,
.
18.证明:∵点D,E,F分别是AB,AC,BC的中点,
∴DE∥CF,DE=BC,DF∥CE,DF=AC,
∴四边形DECF是平行四边形,
∵AC=BC,
∴DE=DF,
∴四边形DFCE是菱形;
19.
【答案】
20.证明:∵DE∥AB,DF∥AC
∴四边形AEDF是平行四边形,∴DF=AE,又∵DE∥AB,∴∠B=∠EDC,又∵AB=AC,∴∠B=∠C,∴∠C=∠EDC,∴DE=CE,∴DF+DE=AE+CE=AC=AB.
21.∵在中,点、分别为、的中点
∴是的中位线
∴
即
∵
∴四边形为平行四边形
∴.
22.【分析】(1)由平行线的性质得出∠DAF=∠AFB,由已知得出∠BAF=∠DAF,得出∠AFB=∠BAF,证出BF=AB=8,即可得出答案;
(2)证明△ABF≌△CDE(ASA),得出AF=CE,证出四边形AFCE是平行四边形,再证明四边形BFDE是平行四边形,得出BE∥DF,得出四边形EGFH是平行四边形,即可得出EF和GH互相平分.
【解答】(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,BC=AD=12,∠BAD=∠BCD,∠ABF=∠CDE,AB=CD,
∴∠DAF=∠AFB,
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∴∠AFB=∠BAF,
∴BF=AB=8,
∴CF=BC﹣BF=12﹣8=4;
(2)证明:∵∠BAD=∠BCD,AF平分∠BAD,CE平分∠BCD,
∴∠BAF=∠DAF=∠FCE=∠DCE,
∵∠DAF=∠AFB,
∴∠FCE=∠AFB,
∴AF∥CE,
?ABCD中,AE∥CF,
∴四边形AFCE是平行四边形,
∴AE=CF,
∴DE=BF,
∵AD∥BC,
∴四边形BFDE是平行四边形,
∴BE∥DF,
∵AF∥CE,
∴四边形EGFH是平行四边形,
∴EF和GH互相平分.
【点评】本题考查了平行四边形的判定与性质、等腰三角形的判定、全等三角形的判定与性质等知识;熟练掌握平行四边形的判定与性质是解题的关键.
23.【分析】(1)由平行线可得四边形OBEC为平行四边形,又矩形对角线互相平分且相等,则可得四边形OBEC为菱形;
(2)由平行线可得四边形OBEC为平行四边形,又正方形对角线互相垂直、平分且相等,则可得四边形OBEC为正方形.
【解答】解:(1)四边形OBEC是菱形.
证明:∵BE∥OC,CE∥OB,
∴四边形OBEC为平行四边形.
又∵四边形ABCD是矩形,
∴OC=OB,
∴平行四边形OBEC为菱形;
(2)四边形OBEC是正方形.
证明:∵BE∥OC,CE∥OB,
∴四边形OBEC为平行四边形.
又∵四边形ABCD是正方形,
∴OC=OB,∠BOC=90°,
∴平行四边形OBEC为正方形.
【点评】本题主要考查了平行四边形的判定,矩形、正方形的性质以及正方形、菱形的判定,应熟练掌握.
24.【分析】(1)先证明四边形ABEF是平行四边形,再证明邻边相等即可证明.
(2)由菱形的对角线平分对角和等边三角形的判定推知△ABE是等边三角形,则AE=AB.
【解答】(1)证明:∵四边形ABCD是平行四边形
∴AD∥BC,
∴∠EBF=∠AFB,
∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠ABF=∠AFB,
∴AB=AF,
∵BO⊥AE,
∴∠AOB=∠EOB=90°,
∵BO=BO,
∴△BOA≌△BOE(ASA),
∴AB=BE,
∴BE=AF,BE∥AF,
∴四边形ABEF是平行四边形,
∵AB=AF.
∴四边形ABEF是菱形.
(2)解:菱形ABEF的周长为16,∠BEF=120°,
∴BE=AB=4,∠AEB=60°.
∴△ABE是等边三角形,则AE=AB=4.
【点评】本题考查平行四边形的性质、菱形的判定和性质、等腰三角形的性质等知识,记住菱形的三种判定方法,属于中考常考题型.
图11
《平行四边形》单元测试
一.选择题(每题3分,共30分)
1.如图,在菱形ABCD中,∠B=60°,AB=4,则以AC为一边的正方形ACEF的周长为( )
A.14
B.15
C.16
D.17
2.
如图,在矩形ABCD中,对角线AC,BD相交于点O,过O的直线EF分别交AB,CD于点E,F,若图中阴影部分的面积为6,则矩形ABCD的面积为( )
A.12
B.18
C.24
D.30
3.
平行四边形ABCD的对角线交于点O,有五个条件:①AC=BD,②∠ABC=90°,③AB=AC,④AB=BC,⑤AC⊥BD,则下列哪个组合可判定这个四边形是正方形?( )
A.①②
B.①③
C.①④
D.④⑤
4.如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=( )
A.90°α
B.90°+
α
C.
α
D.360°α
5.如图,正方形ABCD中,DE=2AE=4,F是BE的中点,点H在CD上,∠EFH=45°,则FH的长度为( )
A.
B.5
C.
D.2
6.如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30°
B.25°
C.20°
D.15°
7.如图,在?ABCD中,AE平分∠BAD交边BC于点E,若AD=8,EC=2,则AB的长是(
)
A.10
B.8
C.6
D.4
8.如图,在菱形ABCD中MN分别在AB、CD上且AM=CN,MN与AC交于点O,连接BO若∠DAC=62°,则∠OBC的度数为( )
A.28°
B.52°
C.62°
D.72°
9.已知平行四边形ABCD的对角线交于点O,则下列命题是假命题的是(
)
A.若AC⊥BD,则平行四边形ABCD是菱形
B.若BO=2AO,则平行四边形ABCD是菱形
C.若AB=AD,则平行四边形ABCD是菱形
D.若∠ABD=∠CBD,则平行四边形ABCD是菱形
10.如图,若要使?ABCD成为菱形,则可添加的条件是(
)
A.AB=CD
B.AD=BC
C.AB=BC
D.AC=BD
二.填空题(每题4分,共20分)
11.如图,□ABCD中,E是BA的中点,连接DE,将△DAE沿DE折叠,使点A落在□ABCD内部的点F处.若∠CBF=25°,则∠FDA的度数为_________.
12.
若以A(-0.5,0),B(2,0),C(0,1)三点为顶点画平行四边形,则第四个顶点不可能在第________象限.
13.如图,矩形ABCD中,E是BC的中点,矩形ABCD的周长是20
cm,AE=5
cm,则AB的长为________
cm.
14.如图①,矩形纸片ABCD中,AB=5,BC=3,先按图②操作:将矩形纸片ABCD沿过点A的直线折叠,使点D落在边AB上的点E处,折痕为AF再按图③操作:沿过点F的直线折叠,使点C落在EF上的点H处,折痕为FG,则A,H两点间
的距离为_________.
15如图,在R△ABC中,∠A=90°,AB=AC,BC=+1,点M,N分别是边BC,
上的动点,沿MN所在的直线折叠∠B,使点B的对应点B始终落在边AC上.若△MBC为直角三角形,则BM的长为_________.
三.解答题(每题10分,共50分)
16.如图,已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图①,点E在CD上,点G在BC的延长线上,判断DM,EM的数量关系与位置关系,请直接写出结论.
(2)如图②,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论.
17.如图,四边形是正方形,为上一点,连接,延长至点,使得,过点作,垂足为,求证:.
18.(6分)如图,在△ABC中,AC=BC,点D,E,F分别是AB,AC,BC的中点,连接DE,DF.求证:四边形DFCE是菱形.
19.
如图,在中,于,于,的两条高相交于,,,求的长.
20.
如图11所示,已知D是等腰三角形ABC底边BC上的一点,点E,F分别在AC,AB上,且DE∥AB,DF∥AC
求证:DE+DF=AB
21.如图,
在中,点、分别为、的中点,点在的延长线上,.
求证:.
22.如图,在?ABCD中,AF平分∠BAD交BC于点F,CE平分∠BCD交AD于点E.
(1)若AD=12,AB=8,求CF的长;
(2)连接BE和AF相交于点G,DF和CE相交于点H,求证:EF和GH互相平分.
23.平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.
(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;
(2)如果四边形ABCD是正方形,四边形OBEC也是正方形吗?如果是,请给予证明;如果不是,请说明理由.
24.已知,如图,在?ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形:
(2)若菱形ABEF的周长为16,∠BEF=120°,求AE的大小.
参考答案
一.选择题
1.D
2.B
3.C
4.
C.
5.
D.
6.
C.
7.
C.
8.A.
9.
B.10.C
二.填空题(共5小题)
11.
(-3,2).
12.三
13.4
14.
【答案】∠BAD=90°(答案不唯一) 【解析】∵?ABCD的对角线AC与BD相交于点O,且AC⊥BD,∴?ABCD是菱形,当∠BAD=90°时,菱形ABCD为正方形.故可添加条件:∠BAD=90°.
15.
12.5
三.解答题(共5小题)
16.解:(1)结论:DM⊥EM,DM=EM.
[解析]延长EM交AD于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,
AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME.
(2)结论不变.DM⊥EM,DM=EM.
证明:延长EM交DA的延长线于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,
AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,
∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME.
17.证明:四边形为正方形,
,,
,
,
,
在和中,,
,
.
18.证明:∵点D,E,F分别是AB,AC,BC的中点,
∴DE∥CF,DE=BC,DF∥CE,DF=AC,
∴四边形DECF是平行四边形,
∵AC=BC,
∴DE=DF,
∴四边形DFCE是菱形;
19.
【答案】
20.证明:∵DE∥AB,DF∥AC
∴四边形AEDF是平行四边形,∴DF=AE,又∵DE∥AB,∴∠B=∠EDC,又∵AB=AC,∴∠B=∠C,∴∠C=∠EDC,∴DE=CE,∴DF+DE=AE+CE=AC=AB.
21.∵在中,点、分别为、的中点
∴是的中位线
∴
即
∵
∴四边形为平行四边形
∴.
参考答案
一.选择题
1.D
2.B
3.C
4.
C.
5.
D.
6.
C.
7.
C.
8.A.
9.
B.10.C
二.填空题(共5小题)
11.
(-3,2).
12.三
13.4
14.
【答案】∠BAD=90°(答案不唯一) 【解析】∵?ABCD的对角线AC与BD相交于点O,且AC⊥BD,∴?ABCD是菱形,当∠BAD=90°时,菱形ABCD为正方形.故可添加条件:∠BAD=90°.
15.
12.5
三.解答题(共5小题)
16.解:(1)结论:DM⊥EM,DM=EM.
[解析]延长EM交AD于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,
AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME.
(2)结论不变.DM⊥EM,DM=EM.
证明:延长EM交DA的延长线于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,
AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,
∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME.
17.证明:四边形为正方形,
,,
,
,
,
在和中,,
,
.
18.证明:∵点D,E,F分别是AB,AC,BC的中点,
∴DE∥CF,DE=BC,DF∥CE,DF=AC,
∴四边形DECF是平行四边形,
∵AC=BC,
∴DE=DF,
∴四边形DFCE是菱形;
19.
【答案】
20.证明:∵DE∥AB,DF∥AC
∴四边形AEDF是平行四边形,∴DF=AE,又∵DE∥AB,∴∠B=∠EDC,又∵AB=AC,∴∠B=∠C,∴∠C=∠EDC,∴DE=CE,∴DF+DE=AE+CE=AC=AB.
21.∵在中,点、分别为、的中点
∴是的中位线
∴
即
∵
∴四边形为平行四边形
∴.
22.【分析】(1)由平行线的性质得出∠DAF=∠AFB,由已知得出∠BAF=∠DAF,得出∠AFB=∠BAF,证出BF=AB=8,即可得出答案;
(2)证明△ABF≌△CDE(ASA),得出AF=CE,证出四边形AFCE是平行四边形,再证明四边形BFDE是平行四边形,得出BE∥DF,得出四边形EGFH是平行四边形,即可得出EF和GH互相平分.
【解答】(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,BC=AD=12,∠BAD=∠BCD,∠ABF=∠CDE,AB=CD,
∴∠DAF=∠AFB,
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∴∠AFB=∠BAF,
∴BF=AB=8,
∴CF=BC﹣BF=12﹣8=4;
(2)证明:∵∠BAD=∠BCD,AF平分∠BAD,CE平分∠BCD,
∴∠BAF=∠DAF=∠FCE=∠DCE,
∵∠DAF=∠AFB,
∴∠FCE=∠AFB,
∴AF∥CE,
?ABCD中,AE∥CF,
∴四边形AFCE是平行四边形,
∴AE=CF,
∴DE=BF,
∵AD∥BC,
∴四边形BFDE是平行四边形,
∴BE∥DF,
∵AF∥CE,
∴四边形EGFH是平行四边形,
∴EF和GH互相平分.
【点评】本题考查了平行四边形的判定与性质、等腰三角形的判定、全等三角形的判定与性质等知识;熟练掌握平行四边形的判定与性质是解题的关键.
23.【分析】(1)由平行线可得四边形OBEC为平行四边形,又矩形对角线互相平分且相等,则可得四边形OBEC为菱形;
(2)由平行线可得四边形OBEC为平行四边形,又正方形对角线互相垂直、平分且相等,则可得四边形OBEC为正方形.
【解答】解:(1)四边形OBEC是菱形.
证明:∵BE∥OC,CE∥OB,
∴四边形OBEC为平行四边形.
又∵四边形ABCD是矩形,
∴OC=OB,
∴平行四边形OBEC为菱形;
(2)四边形OBEC是正方形.
证明:∵BE∥OC,CE∥OB,
∴四边形OBEC为平行四边形.
又∵四边形ABCD是正方形,
∴OC=OB,∠BOC=90°,
∴平行四边形OBEC为正方形.
【点评】本题主要考查了平行四边形的判定,矩形、正方形的性质以及正方形、菱形的判定,应熟练掌握.
24.【分析】(1)先证明四边形ABEF是平行四边形,再证明邻边相等即可证明.
(2)由菱形的对角线平分对角和等边三角形的判定推知△ABE是等边三角形,则AE=AB.
【解答】(1)证明:∵四边形ABCD是平行四边形
∴AD∥BC,
∴∠EBF=∠AFB,
∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠ABF=∠AFB,
∴AB=AF,
∵BO⊥AE,
∴∠AOB=∠EOB=90°,
∵BO=BO,
∴△BOA≌△BOE(ASA),
∴AB=BE,
∴BE=AF,BE∥AF,
∴四边形ABEF是平行四边形,
∵AB=AF.
∴四边形ABEF是菱形.
(2)解:菱形ABEF的周长为16,∠BEF=120°,
∴BE=AB=4,∠AEB=60°.
∴△ABE是等边三角形,则AE=AB=4.
【点评】本题考查平行四边形的性质、菱形的判定和性质、等腰三角形的性质等知识,记住菱形的三种判定方法,属于中考常考题型.
图11
