一次函数(第一课时)正比例函数
图片预览






文档简介
(共22张PPT)
0
x
y
2006年7月12日,我国著名运动员刘翔在瑞士洛桑的田经大奖赛110米栏的决赛中,以12.88秒的成绩打破了尘封13年的世界纪录,为我们中华民族争得了荣誉。在这次决赛中刘翔平均每秒约跑8.54米.
假定刘翔在这次110米栏决赛中奔跑速度是8.54米/秒,那么他奔跑的路程y(单位:米)与奔跑时间x(单位:秒)之间有什么关系?
y= 8.54x (0≤x ≤12.88)
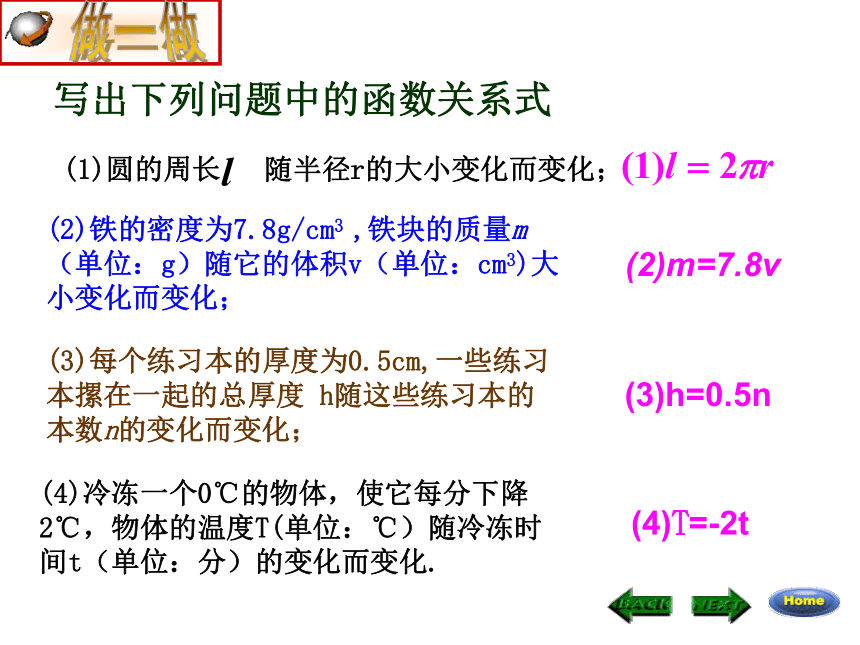
写出下列问题中的函数关系式
(2)铁的密度为7.8g/cm3 ,铁块的质量m(单位:g)随它的体积v(单位:cm3)大小变化而变化;
(3)每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度 h随这些练习本的本数n的变化而变化;
(4)冷冻一个0℃的物体,使它每分下降2℃,物体的温度T(单位:℃)随冷冻时间t(单位:分)的变化而变化.
(2)m=7.8v
(3)h=0.5n
(4)T=-2t
(1)圆的周长 随半径r的大小变化而变化;
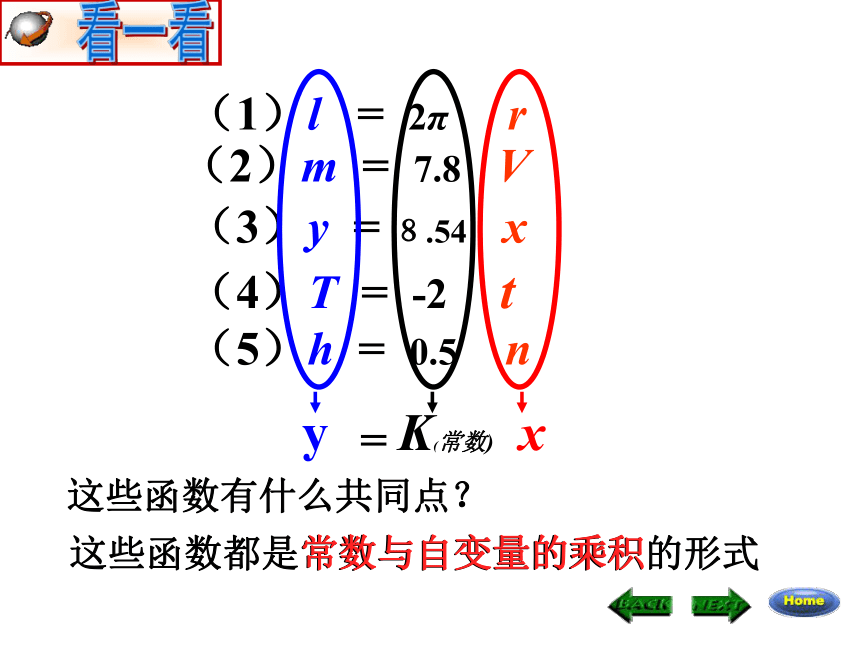
这些函数有什么共同点?
这些函数都是常数与自变量的乘积的形式
(2)m = 7.8 V
(5)h = 0.5 n
(4)T = -2 t
(3)y = 8.54 x
(1)l = 2π r
常数与自变量的乘积
y
K(常数)
x
=
一般地,形如 y=kx(k是常数且k≠0)的函数,叫做正比例函数,其中 k 叫做比例系数.
正比例函数的定义:
下列函数中哪些是正比例函数?
(2)y = x+2
(1)y =2x
(5)y=x2+1
(3)
(4)
(6)
是
是
不是
不是
不是
不是
y
-4
-2
-3
-1
3
2
1
-1 0
-2
-3
1
2
3
4
5
x
-4
-2
0
2
4
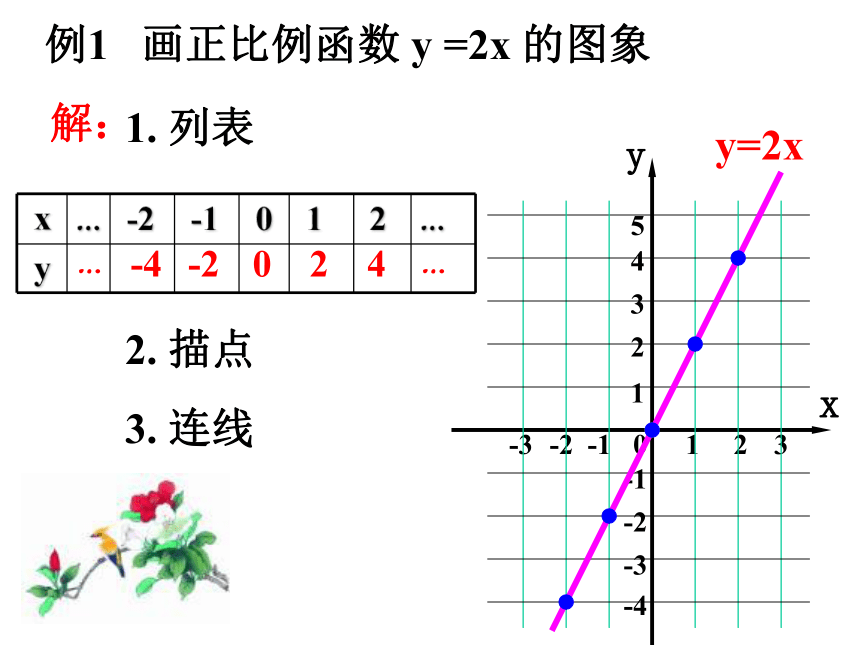
y=2x
x … -2 -1 0 1 2 …
y
例1 画正比例函数 y =2x 的图象
解:
1. 列表
2. 描点
3. 连线
…
…
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
2
3
4
5
x
y
1
y=2x
画出正比例函数 , 的图象?
随堂练习
观 察
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
5
x
y
y=2x
4
3
2
1
比较上面两个函数的图象的相同点与不同点,考虑
两个函数的变化规律.
结论:两图象都是经过原点的 直线 ,函数 的图象从左向右上升_,经过第一三象限;函数
的图象从左向右下降,经过第二四象限.
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
2
3
4
5
x
y
1
画出正比例函数 ,
的图象?
随堂练习
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
5
x
y
y=2x
4
3
2
1
想一想
正比例函数y= kx (k≠0)的图象有什么特征
和性质?
一般地,正比例函数y=kx(k是常数,k≠0)的图象
直线y=kx经过第一、三象限,
直线y=kx经过第二、四象限,
我们称它为直线y=kx.
正比例函数图象的特征及性质
是一条经过原点的直线;
当k >0时,
当k <0时,
从左向右上升,
即随着x的增大y也增大;
从左向右下降,
即随着x的增大y反而减小.
1
k
1
k
x
y
0
y= kx (k>0)
x
y
0
y= kx
(k<0)
经过原点 和点 的直线是哪个函数的图象?通画正比例函数的图象有无简便的办法?
正比例函数y= kx (k≠0) 的图象是经过原点(0,0)和点(1,k)的一条直线。
(0,0)
(1,k)
解:选取两点(0,0) , (1,3)
例2:画函数 y = 3x 的图象
y
-4
-2
-3
-1
3
2
1
-1 0
-2
-3
1
2
3
4
5
x
y=3x
过这两点画直线,
就是函数y= 3x 的图象
y
-4
-2
-3
-1
3
2
1
-1 0
-2
4
1
2
3
4
-5
x
过这两点画直线,
y= x
2
3
例3:画函数 y = x 的图象
2
3
解:选取两点(0,0) , (1, )
2
3
就是函数y= x 的图象
2
3
当k>0时,图象(除原点外)在一,三象限,
x增大时,y的值也增大;
当k<0时,图象(除原点外)在二,四象限,
x增大时,y的值反而减小。
x
y
0
2
4
y = 2x
1
2
2
4
y随x的增大而增大
y随x的增大而减小
y = x
3
2
-3
-6
x
y
0
B
二、四
0
-3
减小
1. 正比例函数y=(m-1)x的图象经过一、三象限,
A. m=1
B. m>1
C. m<1
D. m≥1
3. 函数y=-3x的图象在第 象限内,经过点
2. 正比例函数y=(3-k) x,如果随着x的增大y反而减
小,则k的取值范围是 ______.
k>3
4. 函数y= x的图象在第 象限内,经过点
2
3
(0, )与点(1, ),y随x的增大而 .
(0, )与点(1, ),y随x的增大而 .
三、一
0
2
3
增大
则m的取值范围是( )
3.若 y =5x 3m-2 是正比例函数,
则 m = 。
4.若 是正比例函数,
则 m = 。
1
-2
5.若 是正比例函数,
则 m = 。
2
3 已知y与x-1成正比例,x=8时,y=6,写出y与x之间函数关系式,并分别求出x=4和x=-3时y的值。
解:∵ y与x-1成正比例 ∴y=k(x-1)
∵ 当x=8时,y=6 ∴7k=6 ∴
∴ y与x之间函数关系式是:y= (x-1)
当x=4时,y= ×(4-1)=
当x=-3时,y= ×(-3-1)=
0
x
y
2006年7月12日,我国著名运动员刘翔在瑞士洛桑的田经大奖赛110米栏的决赛中,以12.88秒的成绩打破了尘封13年的世界纪录,为我们中华民族争得了荣誉。在这次决赛中刘翔平均每秒约跑8.54米.
假定刘翔在这次110米栏决赛中奔跑速度是8.54米/秒,那么他奔跑的路程y(单位:米)与奔跑时间x(单位:秒)之间有什么关系?
y= 8.54x (0≤x ≤12.88)
写出下列问题中的函数关系式
(2)铁的密度为7.8g/cm3 ,铁块的质量m(单位:g)随它的体积v(单位:cm3)大小变化而变化;
(3)每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度 h随这些练习本的本数n的变化而变化;
(4)冷冻一个0℃的物体,使它每分下降2℃,物体的温度T(单位:℃)随冷冻时间t(单位:分)的变化而变化.
(2)m=7.8v
(3)h=0.5n
(4)T=-2t
(1)圆的周长 随半径r的大小变化而变化;
这些函数有什么共同点?
这些函数都是常数与自变量的乘积的形式
(2)m = 7.8 V
(5)h = 0.5 n
(4)T = -2 t
(3)y = 8.54 x
(1)l = 2π r
常数与自变量的乘积
y
K(常数)
x
=
一般地,形如 y=kx(k是常数且k≠0)的函数,叫做正比例函数,其中 k 叫做比例系数.
正比例函数的定义:
下列函数中哪些是正比例函数?
(2)y = x+2
(1)y =2x
(5)y=x2+1
(3)
(4)
(6)
是
是
不是
不是
不是
不是
y
-4
-2
-3
-1
3
2
1
-1 0
-2
-3
1
2
3
4
5
x
-4
-2
0
2
4
y=2x
x … -2 -1 0 1 2 …
y
例1 画正比例函数 y =2x 的图象
解:
1. 列表
2. 描点
3. 连线
…
…
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
2
3
4
5
x
y
1
y=2x
画出正比例函数 , 的图象?
随堂练习
观 察
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
5
x
y
y=2x
4
3
2
1
比较上面两个函数的图象的相同点与不同点,考虑
两个函数的变化规律.
结论:两图象都是经过原点的 直线 ,函数 的图象从左向右上升_,经过第一三象限;函数
的图象从左向右下降,经过第二四象限.
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
2
3
4
5
x
y
1
画出正比例函数 ,
的图象?
随堂练习
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
5
x
y
y=2x
4
3
2
1
想一想
正比例函数y= kx (k≠0)的图象有什么特征
和性质?
一般地,正比例函数y=kx(k是常数,k≠0)的图象
直线y=kx经过第一、三象限,
直线y=kx经过第二、四象限,
我们称它为直线y=kx.
正比例函数图象的特征及性质
是一条经过原点的直线;
当k >0时,
当k <0时,
从左向右上升,
即随着x的增大y也增大;
从左向右下降,
即随着x的增大y反而减小.
1
k
1
k
x
y
0
y= kx (k>0)
x
y
0
y= kx
(k<0)
经过原点 和点 的直线是哪个函数的图象?通画正比例函数的图象有无简便的办法?
正比例函数y= kx (k≠0) 的图象是经过原点(0,0)和点(1,k)的一条直线。
(0,0)
(1,k)
解:选取两点(0,0) , (1,3)
例2:画函数 y = 3x 的图象
y
-4
-2
-3
-1
3
2
1
-1 0
-2
-3
1
2
3
4
5
x
y=3x
过这两点画直线,
就是函数y= 3x 的图象
y
-4
-2
-3
-1
3
2
1
-1 0
-2
4
1
2
3
4
-5
x
过这两点画直线,
y= x
2
3
例3:画函数 y = x 的图象
2
3
解:选取两点(0,0) , (1, )
2
3
就是函数y= x 的图象
2
3
当k>0时,图象(除原点外)在一,三象限,
x增大时,y的值也增大;
当k<0时,图象(除原点外)在二,四象限,
x增大时,y的值反而减小。
x
y
0
2
4
y = 2x
1
2
2
4
y随x的增大而增大
y随x的增大而减小
y = x
3
2
-3
-6
x
y
0
B
二、四
0
-3
减小
1. 正比例函数y=(m-1)x的图象经过一、三象限,
A. m=1
B. m>1
C. m<1
D. m≥1
3. 函数y=-3x的图象在第 象限内,经过点
2. 正比例函数y=(3-k) x,如果随着x的增大y反而减
小,则k的取值范围是 ______.
k>3
4. 函数y= x的图象在第 象限内,经过点
2
3
(0, )与点(1, ),y随x的增大而 .
(0, )与点(1, ),y随x的增大而 .
三、一
0
2
3
增大
则m的取值范围是( )
3.若 y =5x 3m-2 是正比例函数,
则 m = 。
4.若 是正比例函数,
则 m = 。
1
-2
5.若 是正比例函数,
则 m = 。
2
3 已知y与x-1成正比例,x=8时,y=6,写出y与x之间函数关系式,并分别求出x=4和x=-3时y的值。
解:∵ y与x-1成正比例 ∴y=k(x-1)
∵ 当x=8时,y=6 ∴7k=6 ∴
∴ y与x之间函数关系式是:y= (x-1)
当x=4时,y= ×(4-1)=
当x=-3时,y= ×(-3-1)=
