一次函数的图象和性质

(共20张PPT)
2012.3.23
1.若正比例函数y=kx（k≠0）经过点（-1，2），则该正比例函数的解析式为y=___________.
2.如图，一次函数y=ax+b的图象经过A、B两点，
则关于x的不等式ax+b<0的解集是 ．
3. 一次函数的图象经过点（1，2），且y随x的增大而减小，则这个函数的解析式可以是 .（任写出一个符合题意即可）
课前回顾
y=-2x
x<2
y=-2x+3（等）
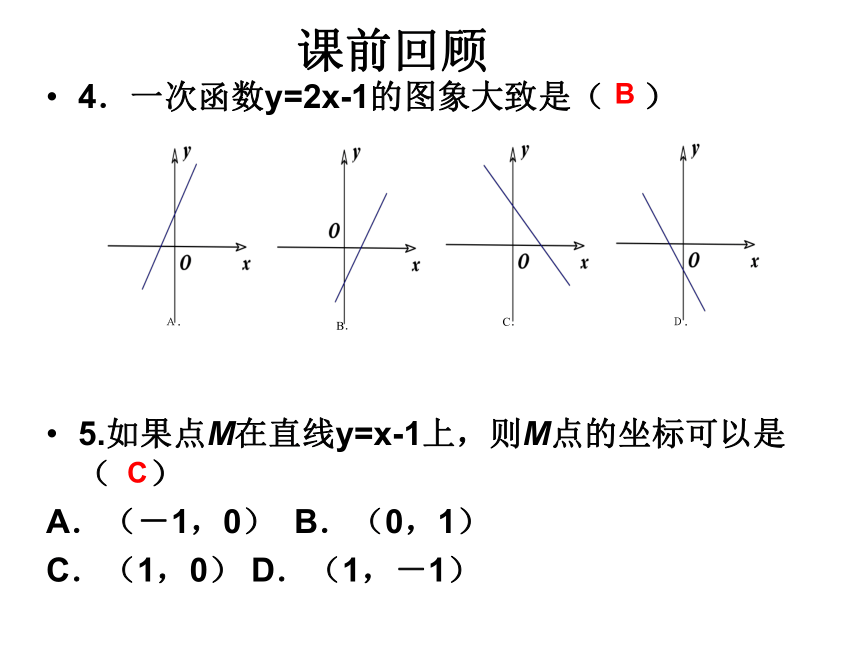
4．一次函数y=2x-1的图象大致是（ ）
5.如果点M在直线y=x-1上，则M点的坐标可以是（ ）
A．（－1，0） B．（0，1）
C．（1，0） D．（1，－1）
课前回顾
Ａ．
B．
C．
Ｄ．
B
C
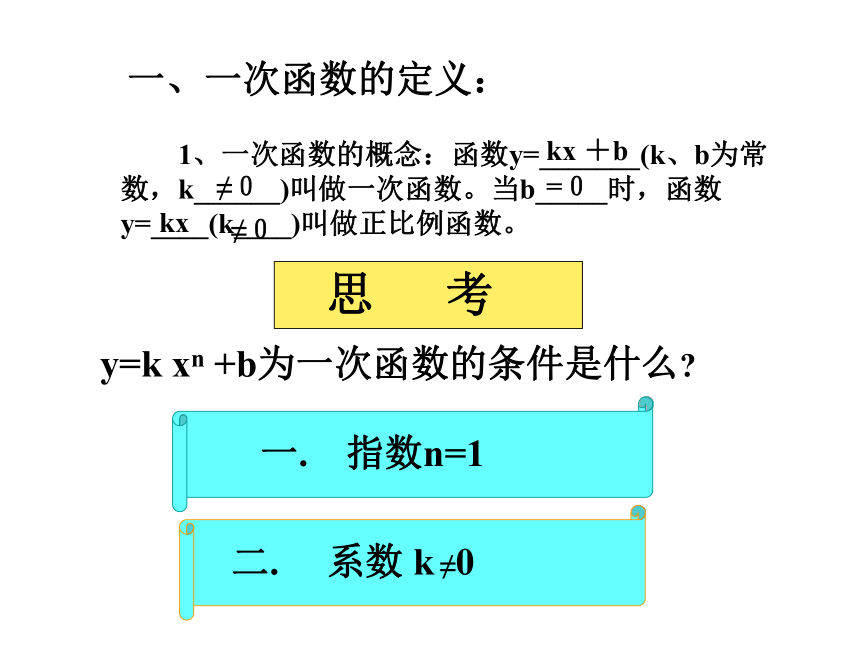
一、一次函数的定义：
　　1、一次函数的概念：函数y=_______(k、b为常数，k______)叫做一次函数。当b_____时，函数y=____(k____)叫做正比例函数。
kx ＋b
≠０
=０
≠０
思 考
kx
y=k xn +b为一次函数的条件是什么
一. 指数n=1
二. 系数 k ≠0
(1). 待定系数法; (2).实际问题的应用
一 次 函 数
正 比 例 函 数
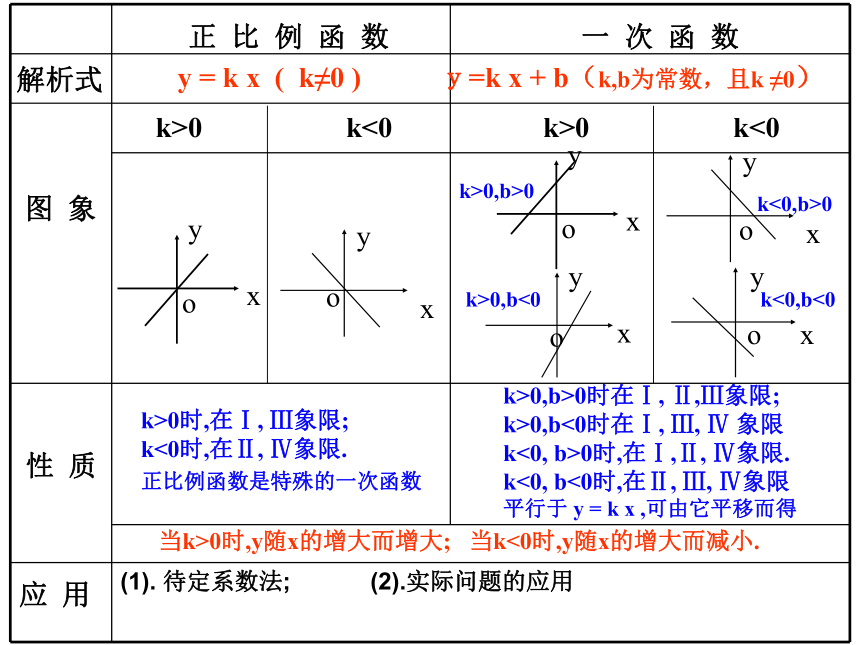
解析式
图 象
性 质
应 用
y = k x ( k≠0 ) ｙ=k x + b（k,b为常数，且k ≠0）
k>0　 k<0 k>0　 k<0
y
x
o
y
x
o
x
y
o
y
x
o
k>0,b>0
k>0,b<0
k<0,b>0
k<0,b<0
y
x
o
x
y
o
k>0时,在Ⅰ, Ⅲ象限;
k<0时,在Ⅱ, Ⅳ象限.
正比例函数是特殊的一次函数
k>0,b>0时在Ⅰ, Ⅱ,Ⅲ象限;
k>0,b<0时在Ⅰ, Ⅲ, Ⅳ 象限
k<0, b>0时,在Ⅰ,Ⅱ, Ⅳ象限.
k<0, b<0时,在Ⅱ, Ⅲ, Ⅳ象限
平行于 y = k x ,可由它平移而得
当k>0时,y随x的增大而增大; 当k<0时,y随x的增大而减小.
一、基础问题
例１　填空题：
(1)　有下列函数：①　　　　　 , ②　y=5x　　　 ,
③　　　 , ④ 。其中过原点的直
线是_____；函数y随x的增大而增大的是___________；函数y随x的增大而减小的是______；图象过第一、二、三象限的是_____。
②
①、②、③
④
③
　　(2)、如果一次函数y=kx-3k+6的图象经过原点，那么
k的值为________。
　　(3)、已知y-1与x成正比例，且x=－2时，y=4，那么y与
x之间的函数关系式为_________________。
k=2
方法：待定系数法：①设；②代；③解；④还原
解：设一次函数解析式为y=kx+b，
把x=1时， y=5；x=6时，y=0代入解析式，得
解得
∴一次函数的解析式为　y= - x+6。
方法：待定系数法：①设；②代；③解；④还原
例２、已知一次函数y=kx+b(k≠0)在x=1时，y=5，且
它的图象与x轴交点的横坐标是６，求这个一次函数的
解析式。
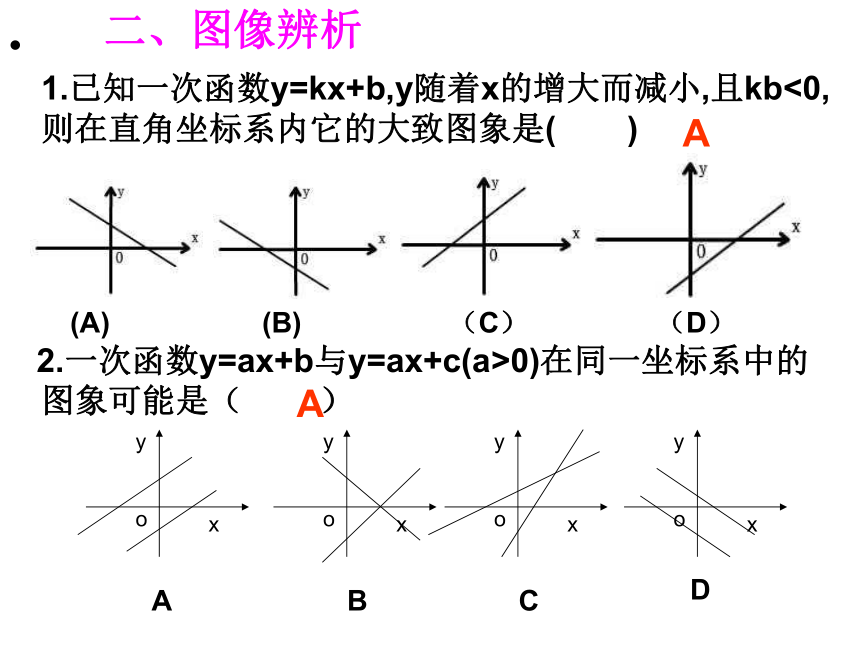
2.一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是（　 　）
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
1.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( 　)
　(A) 　　　　　(B) 　（C） 　　（D）
A
二、图像辨析
A
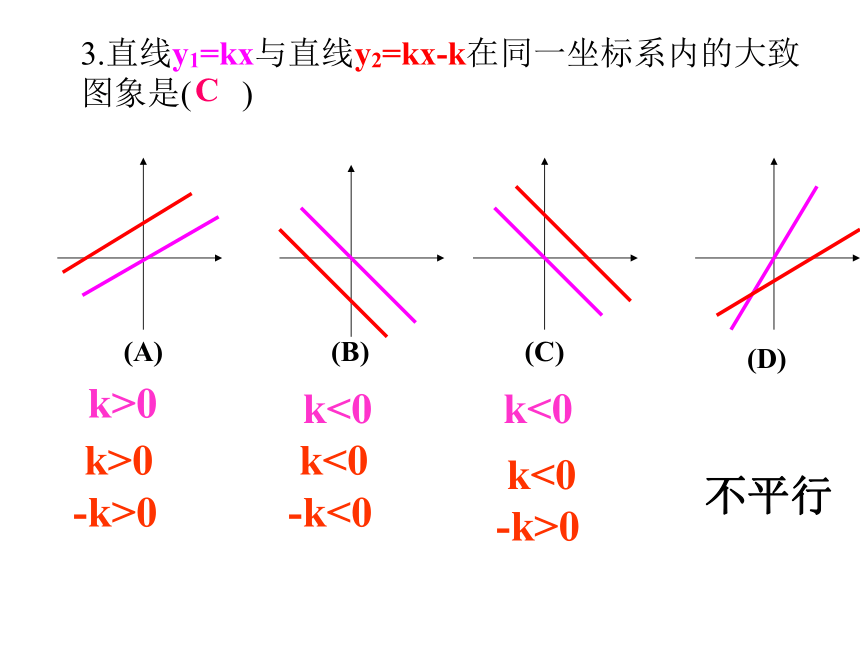
3.直线y1=kx与直线y2=kx-k在同一坐标系内的大致图象是( )
k>0
k<0
k<0
不平行
k>0 -k>0
k<0 -k<0
k<0 -k>0
(A)
(B)
(C)
(D)
C
.1、柴油机在工作时油箱中的余油量Q(千克）与工作时间t（小时）成一次函数关系，当工作开始时油箱中有油40千克，工作3.5小时后，油箱中余油22.5千克
(1)写出余油量Q与时间t的函数关系式;（2）画出这个函数的图象。
解析式为：Q＝－５t+40　　(0≤t≤8)
解：（１）设Ｑ＝kt＋b。把t=0，Q=40；t=3.5，Q=22.5
分别代入上式，得 解得
（２）取点Ａ（０，40），B（8，0）,
然后连成 线段AB,即是所求的图形。
40
8
0
t
Q
图象是包括
两端点的线段
点评:画函数图象时，应根据函数自变量的取值范围来确定图象的范围，比如此题中，因为自变量0≤t≤8，所以图像是一条线段。
三、能力提升1
2.某医药研究所开发了一种新药，在实际验药时发现，如果成人按规定剂量服用，那么每毫升血液中含药量y（毫克）随时间x（时）的变化情况如图所示，当成年人按规定剂量服药后。
（1）服药后____时，血液中含药量最高,达到每毫升_______毫克。
（2）服药5时，血液中含药量为每毫升____毫克。
（3）当x≤2时,y与x之间的函数关系式是_____。
（4）当x≥2时,y与x之间的函数关系式是_________。
（5）如果每毫升血液中含药量3毫克
或3毫克以上时，治疗疾病最有效，
那么这个有效时间是___ 小时。.
x/时
y/毫克
6
3
2
5
O
能力提升2
2
6
3
y=3x
y=-x+8
4
点评（1）根据图像反映的信息解答有关问
题时，首先要弄清楚两坐标轴的实际意义，抓
住几个关键点来解决问题；
（2）特别注意，第5问中由y=3对应的x值有两个；
（3）根据函数图像反映的信息来解答有关问题，比较形象、直观，从中能进一步感受“数形结合思想”。
3.如图，矩形ABCD中，AB=6，动点P以2个单位/s速度沿图甲的边框按B→C→D→A的路径移动，相应的△ABP的面积s关于时间t的函数图象如图乙．根据下图回答问题：
t(s)
s(cm2)
a
5
8
？
o
问题：
（1）P点在整个的移动过程中△ABP的面积是怎样变化的？
（3）图乙中的a在图甲中具有什么实际意义？a的值是多少？
10cm
30
（2）图甲中BC的长是多少？
图甲
图乙
p
能力提升3
解：（1） P点在整个的移动过程中△ABP的面积先逐渐从0增大到30，然后在3分钟内保持30不变，再从30逐渐减小；
（2）BC=10;
(3)a=30. a的值表示点P在CD边上运动时， △ABP的面积;
点评：此类动点问题中，应根据点P的不同运动路线，找出对应的函数图像以及每段图像对应的自变量取值范围，抓住几个关键点，并理解函数图像中横、纵坐标的实际意义。
1.下列函数中，不是一次函数的是 （ ）
2.如图，正比例函数图像经过点A，该函数解析式是______
2
3
o
y
x
4.点P（a,b）点Q（c,d）是一次函数y=-4x+3图像上的两个点，且a3.一次函数y=x+2的图像不经过第____象限
A
C
四
b>d
1.一次函数 y 1=kx+b与y 2=x+a的图像如图所示，则下列结论（1）k<0;(2)a>0;(3)当x<3时，y 1y
x
o
3
y 1=kx+b
y 2=x+a
2.如图，已知一次函数y=kx+b的图像，当x<1时，y的取值范围是____
y
x
o
-4
2
3.一个函数图像过点（-1，2），且y随x增大而减少，则这个函数的解析式是___
1
y<-2
y=-x+1
4.正方形A1B1C1O，A2B2C2C1，A3B3C3C2，
…按如图所示的方式放置．点A1，A2，A3，
…和点C1，C2，C3，…分别在直线y=kx+b
(k＞0)和x轴上，已知点B1(1，1)，
B2(3，2)，则Bn的坐标是_________．
y
x
O
C1
B2
A2
C3
B1
A3
B3
A1
C2
1、直线y=2x+1与y=3x-1的交点P的坐标为____，点P到x轴的距离为_______，点P到y轴的距离为______。
2.一次函数的图象过点(0,3) ,且与两坐标轴围成的三角形面积为 9/4，一次函数的解析式为_________________。
3.如图，将直线OA向上平移1个单位，
得到一个一次函数的图像，那么这个一次
函数的解析式是____________________
y=2x+1
2
5
y=±2x+3
(2, 5)
如图，在平面直角坐标系中，点A的坐标是（4，0），点P在直线y=-x+m上，且AP=OP=4,求m的值。
A
y
x
o
P
如图1，在矩形中，动点R从点N出发，沿N→P→Q→M方向运动至点M处停止．设点R运动的路程为x，△MRN的面积为y，如果y关于x的函数图象如图2所示，则当x=9时，点R应运动到（ ）
A．N处 B．P处 C．Q处 D．M处
Q
P
R
M
N
（图1)
（图2）
4
9
y
x
O
C
若函数y=kx+b的图象平行于y= -2x的图象且经过点（0，4）， 则直线y=kx+b与两坐标轴围成的三角形的面积是：
解:∵y=kx+b图象与y= - 2x图象平行
∴k=-2
∵图像经过点（0，4）
∴b=4
∴此函数的解析式为y= - 2x+4
∵函数y= - 2x+4与两坐标轴的交点为(0,4)
(2,0)
∴S△= ×2 ×4=4
小 结
应用线
一次函数的概念、图象、性质
三个关系 : (1)概念与 k, b
(2)图象与 k, b
(3)面积与交点坐标
应用
知识线
方法线
图象与现实生活的联系