安徽省铜陵市铜官区2020-2021学年七年级下学期期中考试数学试题(word版 含答案)
文档属性
| 名称 | 安徽省铜陵市铜官区2020-2021学年七年级下学期期中考试数学试题(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 602.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-17 19:41:19 | ||
图片预览


文档简介
2020~2021学年度第二学期期中联考试卷
七年级数学试题
(满分:150分
时间:120分钟
)
一、单选题(共10小题,每题4分,计40分,每题只有一个选项是正确的。)
1.下列说法正确的是(
)
A.16的立方根是
B.没有立方根
C.64的平方根是8
D.的算术平方根是2
2.已知点在轴上,则(
)
A.
B.6
C.
D.1
3.点P在y轴左方、x轴上方,距y轴、x轴分别为3、4个单位长度,点P的坐标是(
)
A.(3,–4)
B.(–3,4)
C.(4,–3)
D.(–4,3)
4.如图1,已知AB∥CD∥EF,若∠ABC=α,∠CEF=β,则∠BCE的度数为( )
(图1
)
(图2)
A.α+β
B.β﹣α
C.180°﹣β+α
D.180°﹣α+β
5.下列四个命题
①
过一点有且只有一条直线与已知直线垂直;
②
两条直线被第三条直线所截,内错角相等;
③
一个正实数的算术平方根一定是正实数;
④
是的平方根,其中真命题的个数为(
)
A.
B.
C.
D.
6.如图2,将长方形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
A.112°
B.110°
C.108°
D.106°
7.如图3所示,已知,,,的度数是(
)
(图3)
(图4)
A.
B.
C.
D.
8.在平面直角坐标系中,对于点,我们把点叫做点伴随点.已知点的伴随点为,点的伴随点为,点的伴随点为,…,这样依次得到点,,,…,,….若点的坐标为,点的坐标为(
)
A.
B.
C.
D.
9.估算的运算结果应在(
)
A.3到4之间
B.4到5之间
C.5到6之间
D.6到7之间
10.如图4,在平面直角坐标系xOy中有点P(1,0)。点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,……照此规律,点P第100次跳动至点P100的坐标是(
)
A.(﹣26,50)
B.(﹣25,50)
C.(26,50)
D.(25,50)
二、填空题(共4小题,每题5分,计20分)
11.已知点到两坐标轴的距离相等则点P的坐标为_________________。
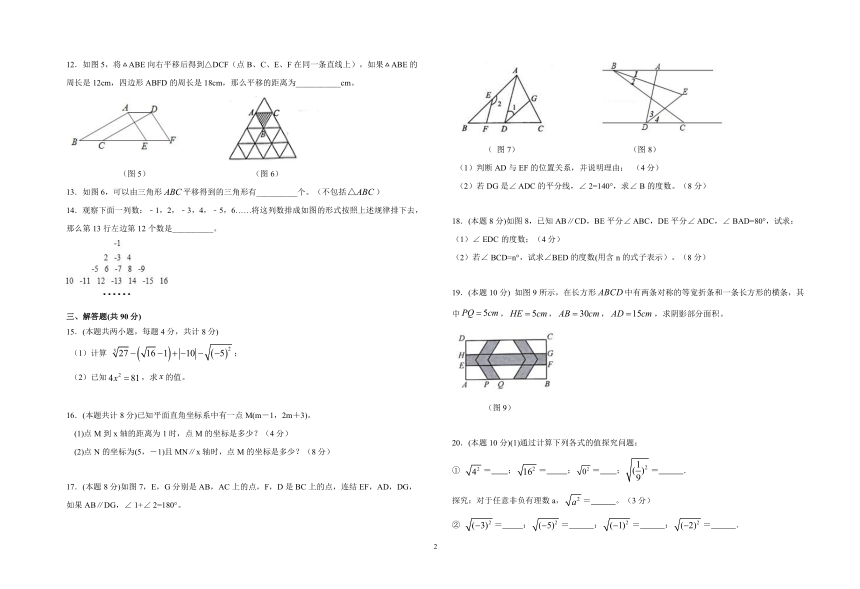
12.如图5,将ABE向右平移后得到△DCF(点B、C、E、F在同一条直线上),如果ABE的周长是12cm,四边形ABFD的周长是18cm,那么平移的距离为___________cm。
(图5)
(图6)
13.如图6,可以由三角形平移得到的三角形有__________个。(不包括)
14.观察下面一列数:﹣1,2,﹣3,4,﹣5,6……将这列数排成如图的形式按照上述规律排下去,那么第13行左边第12个数是__________。
三、解答题(共90分)
15.(本题共两小题,每题4分,共计8分)
(1)计算
;
(2)已知,求的值。
16.(本题共计8分)已知平面直角坐标系中有一点M(m-1,2m+3)。
(1)点M到x轴的距离为1时,点M的坐标是多少?(4分)
(2)点N的坐标为(5,-1)且MN∥x轴时,点M的坐标是多少?(8分)
17.(本题8分)如图7,E,G分别是AB,AC上的点,F,D是BC上的点,连结EF,AD,DG,如果AB∥DG,∠
1+∠
2=180°。
(
图7)
(图8)
(1)判断AD与EF的位置关系,并说明理由;
(4分)
(2)若DG是∠
ADC的平分线,∠
2=140°,求∠
B的度数。(8分)
18.(本题8分)如图8,已知AB∥CD,BE平分∠
ABC,DE平分∠
ADC,∠
BAD=80°,试求:
(1)∠
EDC的度数;(4分)
(2)若∠
BCD=n°,试求∠BED的度数(用含n的式子表示)。(8分)
19.(本题10分)
如图9所示,在长方形中有两条对称的等宽折条和一条长方形的横条,其中,,,,求阴影部分面积。
(图9)
20.(本题10分)(1)通过计算下列各式的值探究问题:
①
=
;=
;=
;=
.
探究:对于任意非负有理数a,=
。(3分)
②
=
;=
;=
;=
.
探究:对于任意负有理数a,=
.
综上,对于任意有理数a,=
。(7分)
(2)应用(1)所得的结论解决问题:有理数a,b在数轴上对应的点的位置如图所示,
化简:--+|a+b|
(10分)。
21.(本题12分)在直角坐标系中,的三个顶点的位置如图10所示,现将沿的方向平移,使得点移至图中的点的位置。
(图10)
(1)在直角坐标系中,画出平移后所得(其中、分别是、的对应点)(3分)
(2)(1)中所得的点,的坐标分别是________,________。(9分)
(3)计算的面积。(12分)
22.(本题共计12分)如图11,在长方形中,为平面直角坐标系的原点,点坐标为,点的坐标为,且,满足,点在第一象限内,点从原点出发,以每秒2个单位长度的速度沿着的线路移动。
(1)点的坐标为___________;(3分)
(2)当点移动4秒时,请指出点的位置,并求出点的坐标;(6分)
(3)在移动过程中,当点到轴的距离为5个单位长度时,求点移动的时间。(12分)
(
图11)
23.(本题14分)如下图1,已知两条直线,被直线所截,分别交于点,点,平分交于点,且。
(补充说明:三角形三个内角和等于1800,例如在中,∠A+∠B+∠C=1800)
(1)判断直线与直线是否平行,并说明理由;(4分)
(2)如图2,点是射线上一动点(不与点,重合),平分交于点,过点作于点,设,.
①
当点在点的右侧时,若,求的度数;(8分)
②
当点在运动过程中,和之间有怎样的数量关系?请写出你的猜想,并加以证明。(14分)
2020-2021学年第二学期期中考试七年级数学参考答案
DDBCBDA
D
D
C
解:和的纵坐标均为,和的纵坐标均为,和的纵坐标均为,因此可以推知和的纵坐标均为;其中4的倍数的跳动都在轴的右侧,那么第100次跳动得到的横坐标也在轴的右侧.横坐标为,横坐标为,横坐标为,以此类推可得到:的横坐标为(是4的倍数).
故点的横坐标为:,纵坐标为:,点第100次跳动至点的坐标为.
11.(1,1)或(2,-2)
解:点到两坐标轴的距离相等.
,
或,
解得或,
当时,,,
此时点P的坐标为,
当时,,,
此时,点P的坐标为,
综上所述,点P的坐标为或.
12.3
13.
14.156
首先观察已知数列中,绝对值为奇数的符号为“-”,绝对值为偶数的符号为“+”,其次观察数列排列中,每一行的第一个数的绝对值,与所在行数的关系:第n行的第一个数的绝对值为:(n-2)2+1,由此可进行判断。
【详解】观察数列,第n行的第一个数的绝对值为:(n-1)2+1
所以第13行的第一个数的绝对值为:(13-1)2+1=145
第13行左边第12个数的绝对值时:145+(12-1)=156
∵156为偶数∴第13行左边第12个数是156
15.(1)5;(2)
详解:(1)
=3-3+10-5
.................................................2分
=5;
...............................................
4分
(2)
系数化为1得,,
.................................................2分
两边同时开平方得
...............................................
4分.
16.(1)
(-2,1)
或(-3,-1)(2)
(-3,-1)
解:(1)∵点M(m﹣1,2m+3),点M到x轴的距离为1,
∴|2m+3|=1,
.................................................2分
解得,m=﹣1或m=﹣2,
当m=﹣1时,点M的坐标为(﹣2,1),
................................................3分
当m=﹣2时,点M的坐标为(﹣3,﹣1);................................................4分
(2)∵点M(m﹣1,2m+3),点N(5,﹣1)且MN∥x轴,
∴2m+3=﹣1,
解得,m=﹣2,故点M的坐标为(﹣3,﹣1).
................................................8分
17.(1)解:AD和EF的位置关系:AD∥EF.
................................................1分
理由:∵AB∥DG
∴∠1=∠BAD
∵∠1+∠2=180°,
∴∠BAD+∠2=180°,
∴AD∥EF.
................................................4分
(2)解:∠1+∠2=180°,∠2=140°
∴∠1=180°-140°=40°,
................................................5分
∵DG平分∠ADC,
∴∠1=∠CDG=40°
................................................6分
∵AB∥DG,
∴∠B=∠CDG=40°.
................................................8分
(1)∠EDC
=40°;(2)∠BED=(40+n)°.
详解:(1)∵,∴.
又∵,∴.
∵平分,∴.
(2)过点作,则有.
又∵,∴.∴.
又∵平分,∴.
∴.∴
19.
经过多次平移变换后,该图案变为如图,
20.(本题共计10分)(1)①4(0.5分,以下3空同分),16,0,;a(此空1分);②3,5,1,2(此前4空每空0.5分);-a;|a|(此两空各1分)
;(2)
-a-3b.(此题计3分)
(1)①②根据要求填空即可;
(2)先根据数轴上点的位置确定:-2<a<-1,0<b<1,a-b<0,a+b<0,再根据(1)中的公式代入计算即可.
解;①=4;=16;=0;=.
探究:对于任意非负有理数a,=a.
②=3;=5;=1;=2.
探究:对于任意负有理数a,=-a.
综上,对于任意有理数a,=|a|.
(2)观察数轴可知:-2<a<-1,0<b<1,a-b<0,a+b<0.
原式=|a|-|b|-|a-b|+|a+b|
=-a-b+a-b-a-b
=-a-3b.
21.解:(1)△A′B′C′如图所示;
................................................3分
(2)由于点A到点A′的平移为向右平移4个单位,再向上平移2个单位,
根据平移的性质可得:B′(5,3),C′(8,4);
................................................9分
(3)△ABC的面积=3×2-×1×2-×1×2-×1×3
=6-1-1-1.5,
=6-3.5,
=2.5.
................................................12分
22.(1)(4,6);(2)(2,6);(3)2.5秒或5.5秒.
解:(1)、满足,
,,
解得,,
点的坐标是
................................................3分
(2)点从原点出发,以每秒2个单位长度的速度沿着的线路移动,
,
,,
当点移动4秒时,在线段上,离点的距离是:,
即当点移动4秒时,此时点在线段上,离点的距离是2个单位长度,点的坐标是;.
...............................................6分
(3)由题意可得,在移动过程中,当点到轴的距离为5个单位长度时,存在两种情况,
第一种情况,当点在上时,
点移动的时间是:秒,
................................................9分
第二种情况,当点在上时.
点移动的时间是:秒,
故在移动过程中,当点到轴的距离为5个单位长度时,点移动的时间是2.5秒或5.5秒.
................................................12分
23.(1)平行(2)①25°;②或
解:(1)平行
................................................1分
平分,
,
又,
,
;
................................................4分
(2)①如图2,,,
,
又平分,平分,
,,
,
又,
中,,
即;
................................................8分
②分两种情况讨论:
如图2,当点在点的右侧时,.
证明:,
,
又平分,平分,
,,
,
又,
中,,
即;
................................................11分
如图3,当点在点的左侧时,.
证明:,
,
又平分,平分,
,,
,
又,
中,,
即.
................................................14分
1
七年级数学试题
(满分:150分
时间:120分钟
)
一、单选题(共10小题,每题4分,计40分,每题只有一个选项是正确的。)
1.下列说法正确的是(
)
A.16的立方根是
B.没有立方根
C.64的平方根是8
D.的算术平方根是2
2.已知点在轴上,则(
)
A.
B.6
C.
D.1
3.点P在y轴左方、x轴上方,距y轴、x轴分别为3、4个单位长度,点P的坐标是(
)
A.(3,–4)
B.(–3,4)
C.(4,–3)
D.(–4,3)
4.如图1,已知AB∥CD∥EF,若∠ABC=α,∠CEF=β,则∠BCE的度数为( )
(图1
)
(图2)
A.α+β
B.β﹣α
C.180°﹣β+α
D.180°﹣α+β
5.下列四个命题
①
过一点有且只有一条直线与已知直线垂直;
②
两条直线被第三条直线所截,内错角相等;
③
一个正实数的算术平方根一定是正实数;
④
是的平方根,其中真命题的个数为(
)
A.
B.
C.
D.
6.如图2,将长方形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
A.112°
B.110°
C.108°
D.106°
7.如图3所示,已知,,,的度数是(
)
(图3)
(图4)
A.
B.
C.
D.
8.在平面直角坐标系中,对于点,我们把点叫做点伴随点.已知点的伴随点为,点的伴随点为,点的伴随点为,…,这样依次得到点,,,…,,….若点的坐标为,点的坐标为(
)
A.
B.
C.
D.
9.估算的运算结果应在(
)
A.3到4之间
B.4到5之间
C.5到6之间
D.6到7之间
10.如图4,在平面直角坐标系xOy中有点P(1,0)。点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,……照此规律,点P第100次跳动至点P100的坐标是(
)
A.(﹣26,50)
B.(﹣25,50)
C.(26,50)
D.(25,50)
二、填空题(共4小题,每题5分,计20分)
11.已知点到两坐标轴的距离相等则点P的坐标为_________________。
12.如图5,将ABE向右平移后得到△DCF(点B、C、E、F在同一条直线上),如果ABE的周长是12cm,四边形ABFD的周长是18cm,那么平移的距离为___________cm。
(图5)
(图6)
13.如图6,可以由三角形平移得到的三角形有__________个。(不包括)
14.观察下面一列数:﹣1,2,﹣3,4,﹣5,6……将这列数排成如图的形式按照上述规律排下去,那么第13行左边第12个数是__________。
三、解答题(共90分)
15.(本题共两小题,每题4分,共计8分)
(1)计算
;
(2)已知,求的值。
16.(本题共计8分)已知平面直角坐标系中有一点M(m-1,2m+3)。
(1)点M到x轴的距离为1时,点M的坐标是多少?(4分)
(2)点N的坐标为(5,-1)且MN∥x轴时,点M的坐标是多少?(8分)
17.(本题8分)如图7,E,G分别是AB,AC上的点,F,D是BC上的点,连结EF,AD,DG,如果AB∥DG,∠
1+∠
2=180°。
(
图7)
(图8)
(1)判断AD与EF的位置关系,并说明理由;
(4分)
(2)若DG是∠
ADC的平分线,∠
2=140°,求∠
B的度数。(8分)
18.(本题8分)如图8,已知AB∥CD,BE平分∠
ABC,DE平分∠
ADC,∠
BAD=80°,试求:
(1)∠
EDC的度数;(4分)
(2)若∠
BCD=n°,试求∠BED的度数(用含n的式子表示)。(8分)
19.(本题10分)
如图9所示,在长方形中有两条对称的等宽折条和一条长方形的横条,其中,,,,求阴影部分面积。
(图9)
20.(本题10分)(1)通过计算下列各式的值探究问题:
①
=
;=
;=
;=
.
探究:对于任意非负有理数a,=
。(3分)
②
=
;=
;=
;=
.
探究:对于任意负有理数a,=
.
综上,对于任意有理数a,=
。(7分)
(2)应用(1)所得的结论解决问题:有理数a,b在数轴上对应的点的位置如图所示,
化简:--+|a+b|
(10分)。
21.(本题12分)在直角坐标系中,的三个顶点的位置如图10所示,现将沿的方向平移,使得点移至图中的点的位置。
(图10)
(1)在直角坐标系中,画出平移后所得(其中、分别是、的对应点)(3分)
(2)(1)中所得的点,的坐标分别是________,________。(9分)
(3)计算的面积。(12分)
22.(本题共计12分)如图11,在长方形中,为平面直角坐标系的原点,点坐标为,点的坐标为,且,满足,点在第一象限内,点从原点出发,以每秒2个单位长度的速度沿着的线路移动。
(1)点的坐标为___________;(3分)
(2)当点移动4秒时,请指出点的位置,并求出点的坐标;(6分)
(3)在移动过程中,当点到轴的距离为5个单位长度时,求点移动的时间。(12分)
(
图11)
23.(本题14分)如下图1,已知两条直线,被直线所截,分别交于点,点,平分交于点,且。
(补充说明:三角形三个内角和等于1800,例如在中,∠A+∠B+∠C=1800)
(1)判断直线与直线是否平行,并说明理由;(4分)
(2)如图2,点是射线上一动点(不与点,重合),平分交于点,过点作于点,设,.
①
当点在点的右侧时,若,求的度数;(8分)
②
当点在运动过程中,和之间有怎样的数量关系?请写出你的猜想,并加以证明。(14分)
2020-2021学年第二学期期中考试七年级数学参考答案
DDBCBDA
D
D
C
解:和的纵坐标均为,和的纵坐标均为,和的纵坐标均为,因此可以推知和的纵坐标均为;其中4的倍数的跳动都在轴的右侧,那么第100次跳动得到的横坐标也在轴的右侧.横坐标为,横坐标为,横坐标为,以此类推可得到:的横坐标为(是4的倍数).
故点的横坐标为:,纵坐标为:,点第100次跳动至点的坐标为.
11.(1,1)或(2,-2)
解:点到两坐标轴的距离相等.
,
或,
解得或,
当时,,,
此时点P的坐标为,
当时,,,
此时,点P的坐标为,
综上所述,点P的坐标为或.
12.3
13.
14.156
首先观察已知数列中,绝对值为奇数的符号为“-”,绝对值为偶数的符号为“+”,其次观察数列排列中,每一行的第一个数的绝对值,与所在行数的关系:第n行的第一个数的绝对值为:(n-2)2+1,由此可进行判断。
【详解】观察数列,第n行的第一个数的绝对值为:(n-1)2+1
所以第13行的第一个数的绝对值为:(13-1)2+1=145
第13行左边第12个数的绝对值时:145+(12-1)=156
∵156为偶数∴第13行左边第12个数是156
15.(1)5;(2)
详解:(1)
=3-3+10-5
.................................................2分
=5;
...............................................
4分
(2)
系数化为1得,,
.................................................2分
两边同时开平方得
...............................................
4分.
16.(1)
(-2,1)
或(-3,-1)(2)
(-3,-1)
解:(1)∵点M(m﹣1,2m+3),点M到x轴的距离为1,
∴|2m+3|=1,
.................................................2分
解得,m=﹣1或m=﹣2,
当m=﹣1时,点M的坐标为(﹣2,1),
................................................3分
当m=﹣2时,点M的坐标为(﹣3,﹣1);................................................4分
(2)∵点M(m﹣1,2m+3),点N(5,﹣1)且MN∥x轴,
∴2m+3=﹣1,
解得,m=﹣2,故点M的坐标为(﹣3,﹣1).
................................................8分
17.(1)解:AD和EF的位置关系:AD∥EF.
................................................1分
理由:∵AB∥DG
∴∠1=∠BAD
∵∠1+∠2=180°,
∴∠BAD+∠2=180°,
∴AD∥EF.
................................................4分
(2)解:∠1+∠2=180°,∠2=140°
∴∠1=180°-140°=40°,
................................................5分
∵DG平分∠ADC,
∴∠1=∠CDG=40°
................................................6分
∵AB∥DG,
∴∠B=∠CDG=40°.
................................................8分
(1)∠EDC
=40°;(2)∠BED=(40+n)°.
详解:(1)∵,∴.
又∵,∴.
∵平分,∴.
(2)过点作,则有.
又∵,∴.∴.
又∵平分,∴.
∴.∴
19.
经过多次平移变换后,该图案变为如图,
20.(本题共计10分)(1)①4(0.5分,以下3空同分),16,0,;a(此空1分);②3,5,1,2(此前4空每空0.5分);-a;|a|(此两空各1分)
;(2)
-a-3b.(此题计3分)
(1)①②根据要求填空即可;
(2)先根据数轴上点的位置确定:-2<a<-1,0<b<1,a-b<0,a+b<0,再根据(1)中的公式代入计算即可.
解;①=4;=16;=0;=.
探究:对于任意非负有理数a,=a.
②=3;=5;=1;=2.
探究:对于任意负有理数a,=-a.
综上,对于任意有理数a,=|a|.
(2)观察数轴可知:-2<a<-1,0<b<1,a-b<0,a+b<0.
原式=|a|-|b|-|a-b|+|a+b|
=-a-b+a-b-a-b
=-a-3b.
21.解:(1)△A′B′C′如图所示;
................................................3分
(2)由于点A到点A′的平移为向右平移4个单位,再向上平移2个单位,
根据平移的性质可得:B′(5,3),C′(8,4);
................................................9分
(3)△ABC的面积=3×2-×1×2-×1×2-×1×3
=6-1-1-1.5,
=6-3.5,
=2.5.
................................................12分
22.(1)(4,6);(2)(2,6);(3)2.5秒或5.5秒.
解:(1)、满足,
,,
解得,,
点的坐标是
................................................3分
(2)点从原点出发,以每秒2个单位长度的速度沿着的线路移动,
,
,,
当点移动4秒时,在线段上,离点的距离是:,
即当点移动4秒时,此时点在线段上,离点的距离是2个单位长度,点的坐标是;.
...............................................6分
(3)由题意可得,在移动过程中,当点到轴的距离为5个单位长度时,存在两种情况,
第一种情况,当点在上时,
点移动的时间是:秒,
................................................9分
第二种情况,当点在上时.
点移动的时间是:秒,
故在移动过程中,当点到轴的距离为5个单位长度时,点移动的时间是2.5秒或5.5秒.
................................................12分
23.(1)平行(2)①25°;②或
解:(1)平行
................................................1分
平分,
,
又,
,
;
................................................4分
(2)①如图2,,,
,
又平分,平分,
,,
,
又,
中,,
即;
................................................8分
②分两种情况讨论:
如图2,当点在点的右侧时,.
证明:,
,
又平分,平分,
,,
,
又,
中,,
即;
................................................11分
如图3,当点在点的左侧时,.
证明:,
,
又平分,平分,
,,
,
又,
中,,
即.
................................................14分
1
同课章节目录
