第8章立体几何初步 章节复习总结 讲义-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册Word
文档属性
| 名称 | 第8章立体几何初步 章节复习总结 讲义-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册Word |  | |
| 格式 | docx | ||
| 文件大小 | 237.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-18 14:31:02 | ||
图片预览



文档简介
1、了解基本立体图形
2、掌握简单几何体的表面积与体积
3、理解空间直线、平面、点之间的平行、垂直位置关系
一、基本立体图形
1棱柱的结构特征
一般地,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互侧相平行,由这些面所围成的几何体叫做棱柱.
2.棱锥的结构特征
一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥
.这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点.相邻侧面的公共边叫做棱锥的侧棱;
3.圆柱的结构特征
以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱.旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;平行于轴的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线.
4.圆锥的结构特征
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体叫做圆锥.
5.棱台于圆台的结构特征
用一个平行于棱锥底面的平面去截棱锥,底面和截面之间那部分,这样的几何体叫做棱台在棱台中,原棱锥的底面和截面分别叫做棱台的下底面和上底面,棱台也有侧面、侧棱、顶点.
6.球的结构
以半圆的直径所在直线为旋转轴.半圆面旋转一周形成的几何体叫做球体.简称球.半圆的圆心叫做球的球心.半圆的半径叫做球的半径.半圆的直径叫做球的直径.
二、直观图
定义:直观图是观察者站在某一点观察一个空间几何图获得的图形,画立体图形的直观图,实际上是把不完全在同一平面内的点的集合,用同一平面内的点表示。
因此,直观图汪汪与立体图形的真实形状不完全相同。
在立体几何中,立体图形的直观图通常是在平行投影下得到的平面图形
画法:斜二测画法和正等测画法.
1、斜二测画法规则
(1)在己知图形中取互相重直的x轴或y轴,两轴相交于点O,画直观图时,把它们画成对应的x,轴与y'轴,两轴相交于点O,,且=45°(或135°),它们确定的平面表示水平面
(2)已知图形中平行于x轴或y轴的线段。在直观图中分剔画成平行于x,轴与y,轴的线段
(3)已知图形中平行于x轴的线段,在直观图中保持原长度不变,平行于y轴的线段,在直观图中长度为原来的一半
三、棱柱、棱锥、棱台的表面积
多面体的表面积就是围成多面体各个面的面积的和,棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和
1.棱柱、棱锥、棱台的体积
棱柱:柱体的底面面积为S,高为h,则V=Sh
棱锥:椎体的底面面积为S,高为h,则V=Sh
棱台:台体的上、下底面面积分别为,,高为h,则
2.圆柱、圆锥、圆台、球的表面积与体积
表面积
(1)圆柱表面积:(r是底面半径,l是母线长)
(2)圆锥表面积:=(r是底面半径,l是母线长)
(3)圆台表面积:(分别是上、下底面半径,是母线长)
(4)球的表面积:
3.体积
(1)圆柱体积:(r是底面半径,h是高)
(2)圆锥体积:(r是底面半径,h是高)
(3)圆台体积:(分别是上、下底面半径,是高)
(4)球的体积:
4.平面
三个基本事实
过不在一条直线上的三点,有且只有一个平面。(不共线的三点确定一个平面)
(2)如果一条直线上两点在一个平面内,那么这条直线在此平面内。
(3)如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
2.三个推论
(1)经过一条直线和这条直线外一点,有且只有一个平面
经过两条相交直线,有且只有一个平面
经过两条平行直线,有且只有一个平面
四、空间点、直线、平面之间的位置关系
空间中直线与直线的位置关系
异面直线
定义:不同在任何一个平面内的两条直线叫做异面直线
空间中两条直线的位置关系
相交直线:在同一平面内,有且只有一个公共点
平行直线:在同一平面内,没有公共点
异面直线:不同在任何一个平面内,没有公共点
空间中直线与平面的位置关系
直线在平面内——有无数个公共点
直线与平面相交——有且只有一个公共点
直线与平面平行——没有公共点
空间中平面与平面的位置关系
两个平面平行——没有公共点
两个平面相交——有一条公共直线
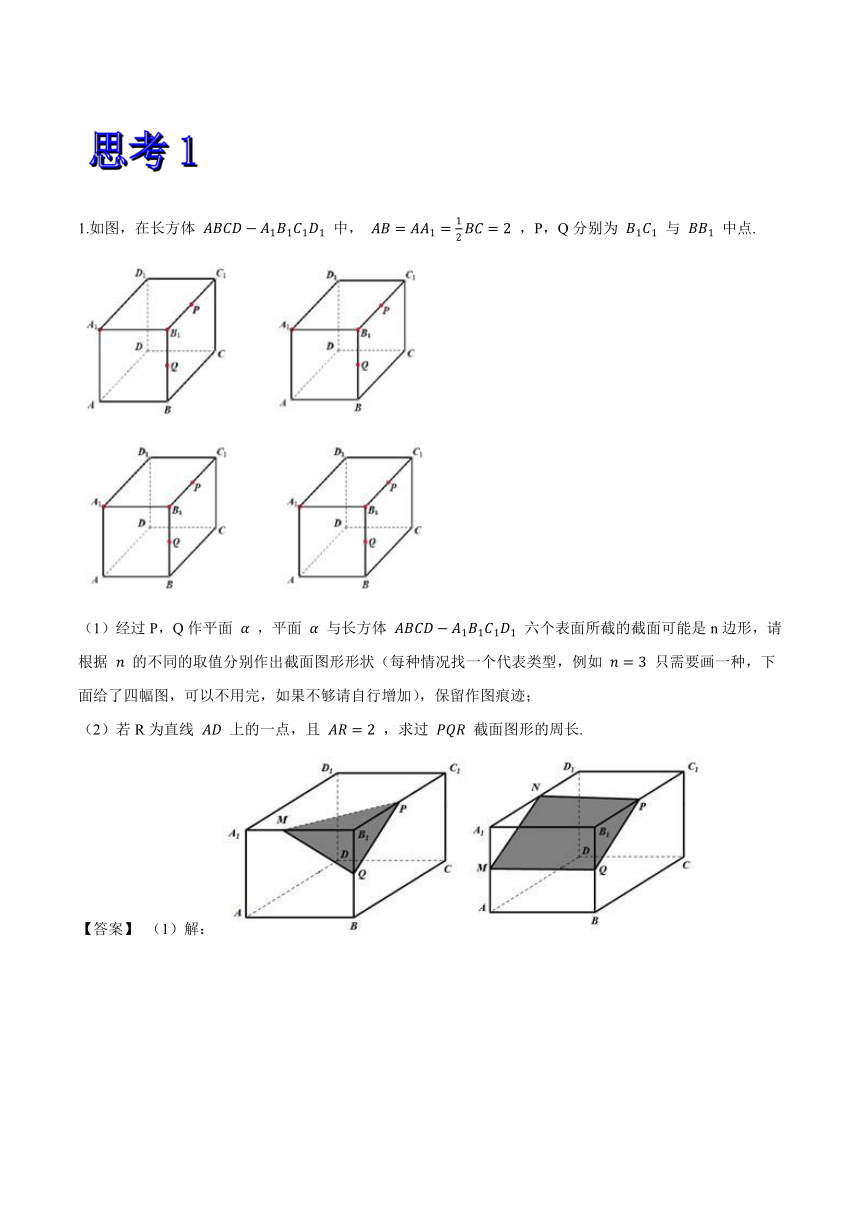
1.如图,在长方体
中,
,P,Q分别为
与
中点.
???
??????
(1)经过P,Q作平面
,平面
与长方体
六个表面所截的截面可能是n边形,请根据
的不同的取值分别作出截面图形形状(每种情况找一个代表类型,例如
只需要画一种,下面给了四幅图,可以不用完,如果不够请自行增加),保留作图痕迹;
(2)若R为直线
上的一点,且
,求过
截面图形的周长.
【答案】
(1)解:
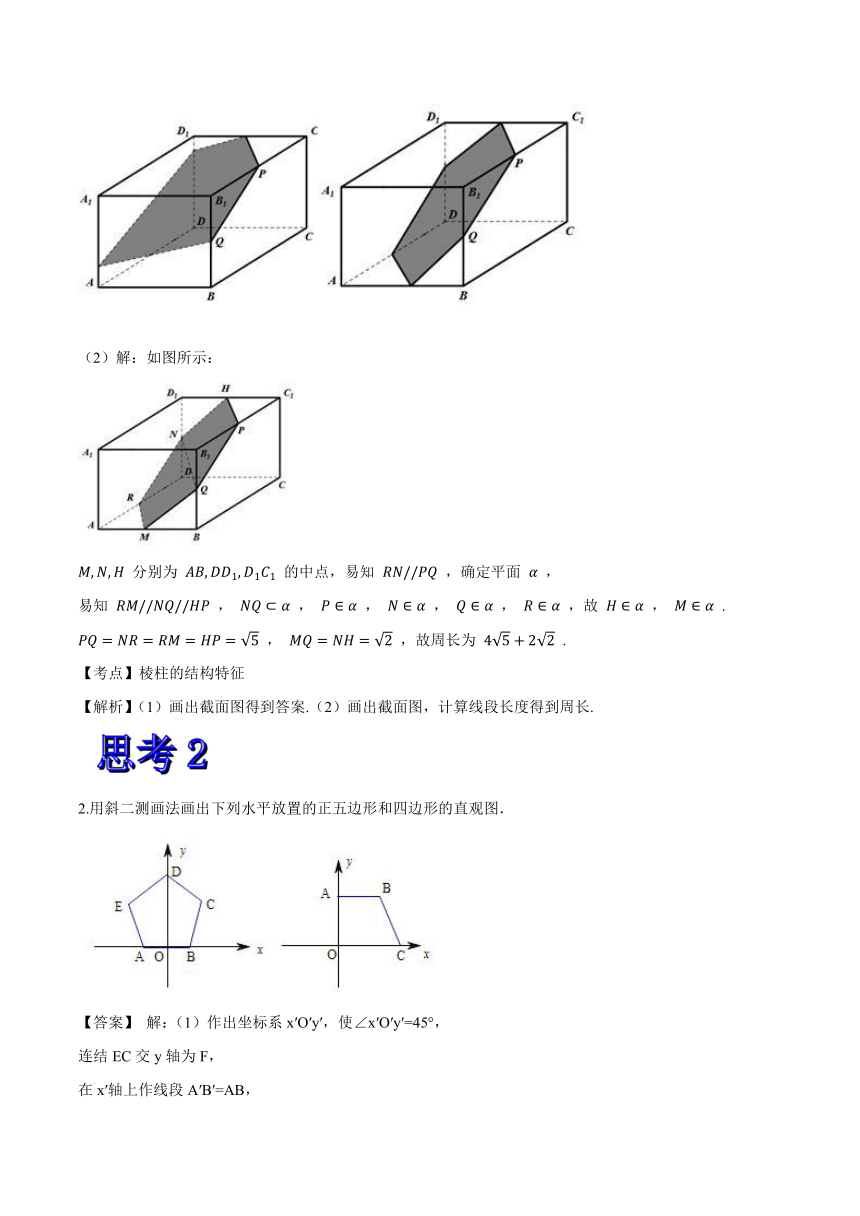
(2)解:如图所示:
分别为
的中点,易知
,确定平面
,
易知
,
,
,
,
,
,故
,
.
,
,故周长为
.
【考点】棱柱的结构特征
【解析】(1)画出截面图得到答案.(2)画出截面图,计算线段长度得到周长.
2.用斜二测画法画出下列水平放置的正五边形和四边形的直观图.
【答案】
解:(1)作出坐标系x′O′y′,使∠x′O′y′=45°,
连结EC交y轴为F,
在x′轴上作线段A′B′=AB,
则y′轴上分别作线段O′D′=OD,O′F′=OF,
过F′作线段E′C′=EC,且E′C′∥O′x′,
连结A′B′C′D′E′,即为正五边形的直观图.
(2)作出坐标系x′O′y′,使∠x′O′y′=45°,
在x′轴上作线段O′C′=OC,
则y′轴上分别作线段O′A′=OA,
过A′作线段A′B′=AB,且A′B′∥O′x′,
连结A′B′C′O′,即为四边形的直观图.
【考点】斜二测法画直观图
【解析】根据斜二测画法的原则即可得到结论.
3.如图,已知四棱台的两底面均为正方形,且边长分别为
和
,侧面积为
,求其体积
【答案】
解:取
的中点
,
的中点
,上、下底面的中心
,则
为斜高,四边形
为直角梯形,
∵
,
∴
,
在直角梯形
中,
,
,
∴
,
故该四棱台的体积为
【考点】棱柱、棱锥、棱台的体积
【解析】取
的中点
,
的中点
,上、下底面的中心
,根据侧面积求出
,再求出棱台的高,即可求出体积.
4.
(1)用符号表示下来语句,并画出同时满足这四个语句的一个几何图形:
①直线
在平面
内;
②直线m不在平面
内;
③直线m与平面
交于点A;
④直线l不经过点A.
(2)如图,在长方体
中,
为棱
的中点,F为棱
的三等分点,画出由
三点所确定的平面
与平面
的交线.(保留作图痕迹)
【答案】
(1)解:
;
;
;
;示意图如下:
(2)解:如图,直线IL即为所求.
【考点】平面的基本性质及推论,空间中直线与平面之间的位置关系
【解析】(1)根据题意,作出示意图即可;(2)根据题意,作出示意图即可.
1.如果一个四面体的三个面是直角三角形,则其第四个面不可能是(???
)
A.?直角三角形????????????????????B.?等边三角形????????????????????C.?等腰直角三角形????????????????????D.?钝角三角形
2.如图,一个四棱柱形容器中盛有水,在底面
中,
,
,
,侧棱
,若侧面
水平放置时,水面恰好过
的中点,那么当底面
水平放置时,水面高为(???
)
A.?2???????????????????????????????????????????B.????????????????????????????????????????????C.?3???????????????????????????????????????????D.?
3.三个平面将空间分成n个部分,则n不可能是(???
)
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
12.在空间中,设
是不同的直线,
表示不同的平面,则下列命题正确的是
(???
)
A.?若
,则
????????????????????????????????????B.?若
,则
C.?若
,则
???????????????????????????????D.?若
,则
参考答案
1.【答案】
D
【解析】
当
,
,
且
时,满足题意,四面体
的三个面是直角三角形.
因为
,
平面
,
平面
.
所以
平面
又因为
平面
所以
因为
,
平面
,
平面
.
所以
平面
因为
平面
所以
又因为
所以
为等腰直角三角形.
则第四个面可能为直角三角形或等腰直角三角形.
当
,
,
且
时
则
则第四个面可能等边三角形
综上所述,第四个面不可能是钝角三角形.
2.【答案】
B
【解析】
设四棱柱的底面梯形的高为
,
的中点分别为
,
所求的水面高为h,
则水的体积
,
所以
,
3.【答案】
A
【解析】
按照三个平面中平行的个数来分类:(1)三个平面两两平行,如图1,可将空间分成4部分;
;(2)两个平面平行,第三个平面与这两个平行平面相交,如图2,可将空间分成6部分;
;(3)三个平面中没有平行的平面:(i)三个平面两两相交且交线互相平行,如图3,可将空间分成7部分;
(ii)三个平面两两相交且三条交线交于一点,如图4,可将空间分成8部分.
(iii)三个平面两两相交且交线重合,如图5,可将空间分成6部分;
综上,可以为4,6,7,8部分,不能为5部分,
4.【答案】
D
【解析】
对于A,若
,可得
或
,A不符合题意;
对于B,若
,可得
或
,B不符合题意;
对于C,若
,则
,或
,或
与
相交,C不符合题意;
对于D,若
,则
,正确.
2、掌握简单几何体的表面积与体积
3、理解空间直线、平面、点之间的平行、垂直位置关系
一、基本立体图形
1棱柱的结构特征
一般地,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互侧相平行,由这些面所围成的几何体叫做棱柱.
2.棱锥的结构特征
一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥
.这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点.相邻侧面的公共边叫做棱锥的侧棱;
3.圆柱的结构特征
以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱.旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;平行于轴的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线.
4.圆锥的结构特征
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体叫做圆锥.
5.棱台于圆台的结构特征
用一个平行于棱锥底面的平面去截棱锥,底面和截面之间那部分,这样的几何体叫做棱台在棱台中,原棱锥的底面和截面分别叫做棱台的下底面和上底面,棱台也有侧面、侧棱、顶点.
6.球的结构
以半圆的直径所在直线为旋转轴.半圆面旋转一周形成的几何体叫做球体.简称球.半圆的圆心叫做球的球心.半圆的半径叫做球的半径.半圆的直径叫做球的直径.
二、直观图
定义:直观图是观察者站在某一点观察一个空间几何图获得的图形,画立体图形的直观图,实际上是把不完全在同一平面内的点的集合,用同一平面内的点表示。
因此,直观图汪汪与立体图形的真实形状不完全相同。
在立体几何中,立体图形的直观图通常是在平行投影下得到的平面图形
画法:斜二测画法和正等测画法.
1、斜二测画法规则
(1)在己知图形中取互相重直的x轴或y轴,两轴相交于点O,画直观图时,把它们画成对应的x,轴与y'轴,两轴相交于点O,,且=45°(或135°),它们确定的平面表示水平面
(2)已知图形中平行于x轴或y轴的线段。在直观图中分剔画成平行于x,轴与y,轴的线段
(3)已知图形中平行于x轴的线段,在直观图中保持原长度不变,平行于y轴的线段,在直观图中长度为原来的一半
三、棱柱、棱锥、棱台的表面积
多面体的表面积就是围成多面体各个面的面积的和,棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和
1.棱柱、棱锥、棱台的体积
棱柱:柱体的底面面积为S,高为h,则V=Sh
棱锥:椎体的底面面积为S,高为h,则V=Sh
棱台:台体的上、下底面面积分别为,,高为h,则
2.圆柱、圆锥、圆台、球的表面积与体积
表面积
(1)圆柱表面积:(r是底面半径,l是母线长)
(2)圆锥表面积:=(r是底面半径,l是母线长)
(3)圆台表面积:(分别是上、下底面半径,是母线长)
(4)球的表面积:
3.体积
(1)圆柱体积:(r是底面半径,h是高)
(2)圆锥体积:(r是底面半径,h是高)
(3)圆台体积:(分别是上、下底面半径,是高)
(4)球的体积:
4.平面
三个基本事实
过不在一条直线上的三点,有且只有一个平面。(不共线的三点确定一个平面)
(2)如果一条直线上两点在一个平面内,那么这条直线在此平面内。
(3)如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
2.三个推论
(1)经过一条直线和这条直线外一点,有且只有一个平面
经过两条相交直线,有且只有一个平面
经过两条平行直线,有且只有一个平面
四、空间点、直线、平面之间的位置关系
空间中直线与直线的位置关系
异面直线
定义:不同在任何一个平面内的两条直线叫做异面直线
空间中两条直线的位置关系
相交直线:在同一平面内,有且只有一个公共点
平行直线:在同一平面内,没有公共点
异面直线:不同在任何一个平面内,没有公共点
空间中直线与平面的位置关系
直线在平面内——有无数个公共点
直线与平面相交——有且只有一个公共点
直线与平面平行——没有公共点
空间中平面与平面的位置关系
两个平面平行——没有公共点
两个平面相交——有一条公共直线
1.如图,在长方体
中,
,P,Q分别为
与
中点.
???
??????
(1)经过P,Q作平面
,平面
与长方体
六个表面所截的截面可能是n边形,请根据
的不同的取值分别作出截面图形形状(每种情况找一个代表类型,例如
只需要画一种,下面给了四幅图,可以不用完,如果不够请自行增加),保留作图痕迹;
(2)若R为直线
上的一点,且
,求过
截面图形的周长.
【答案】
(1)解:
(2)解:如图所示:
分别为
的中点,易知
,确定平面
,
易知
,
,
,
,
,
,故
,
.
,
,故周长为
.
【考点】棱柱的结构特征
【解析】(1)画出截面图得到答案.(2)画出截面图,计算线段长度得到周长.
2.用斜二测画法画出下列水平放置的正五边形和四边形的直观图.
【答案】
解:(1)作出坐标系x′O′y′,使∠x′O′y′=45°,
连结EC交y轴为F,
在x′轴上作线段A′B′=AB,
则y′轴上分别作线段O′D′=OD,O′F′=OF,
过F′作线段E′C′=EC,且E′C′∥O′x′,
连结A′B′C′D′E′,即为正五边形的直观图.
(2)作出坐标系x′O′y′,使∠x′O′y′=45°,
在x′轴上作线段O′C′=OC,
则y′轴上分别作线段O′A′=OA,
过A′作线段A′B′=AB,且A′B′∥O′x′,
连结A′B′C′O′,即为四边形的直观图.
【考点】斜二测法画直观图
【解析】根据斜二测画法的原则即可得到结论.
3.如图,已知四棱台的两底面均为正方形,且边长分别为
和
,侧面积为
,求其体积
【答案】
解:取
的中点
,
的中点
,上、下底面的中心
,则
为斜高,四边形
为直角梯形,
∵
,
∴
,
在直角梯形
中,
,
,
∴
,
故该四棱台的体积为
【考点】棱柱、棱锥、棱台的体积
【解析】取
的中点
,
的中点
,上、下底面的中心
,根据侧面积求出
,再求出棱台的高,即可求出体积.
4.
(1)用符号表示下来语句,并画出同时满足这四个语句的一个几何图形:
①直线
在平面
内;
②直线m不在平面
内;
③直线m与平面
交于点A;
④直线l不经过点A.
(2)如图,在长方体
中,
为棱
的中点,F为棱
的三等分点,画出由
三点所确定的平面
与平面
的交线.(保留作图痕迹)
【答案】
(1)解:
;
;
;
;示意图如下:
(2)解:如图,直线IL即为所求.
【考点】平面的基本性质及推论,空间中直线与平面之间的位置关系
【解析】(1)根据题意,作出示意图即可;(2)根据题意,作出示意图即可.
1.如果一个四面体的三个面是直角三角形,则其第四个面不可能是(???
)
A.?直角三角形????????????????????B.?等边三角形????????????????????C.?等腰直角三角形????????????????????D.?钝角三角形
2.如图,一个四棱柱形容器中盛有水,在底面
中,
,
,
,侧棱
,若侧面
水平放置时,水面恰好过
的中点,那么当底面
水平放置时,水面高为(???
)
A.?2???????????????????????????????????????????B.????????????????????????????????????????????C.?3???????????????????????????????????????????D.?
3.三个平面将空间分成n个部分,则n不可能是(???
)
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
12.在空间中,设
是不同的直线,
表示不同的平面,则下列命题正确的是
(???
)
A.?若
,则
????????????????????????????????????B.?若
,则
C.?若
,则
???????????????????????????????D.?若
,则
参考答案
1.【答案】
D
【解析】
当
,
,
且
时,满足题意,四面体
的三个面是直角三角形.
因为
,
平面
,
平面
.
所以
平面
又因为
平面
所以
因为
,
平面
,
平面
.
所以
平面
因为
平面
所以
又因为
所以
为等腰直角三角形.
则第四个面可能为直角三角形或等腰直角三角形.
当
,
,
且
时
则
则第四个面可能等边三角形
综上所述,第四个面不可能是钝角三角形.
2.【答案】
B
【解析】
设四棱柱的底面梯形的高为
,
的中点分别为
,
所求的水面高为h,
则水的体积
,
所以
,
3.【答案】
A
【解析】
按照三个平面中平行的个数来分类:(1)三个平面两两平行,如图1,可将空间分成4部分;
;(2)两个平面平行,第三个平面与这两个平行平面相交,如图2,可将空间分成6部分;
;(3)三个平面中没有平行的平面:(i)三个平面两两相交且交线互相平行,如图3,可将空间分成7部分;
(ii)三个平面两两相交且三条交线交于一点,如图4,可将空间分成8部分.
(iii)三个平面两两相交且交线重合,如图5,可将空间分成6部分;
综上,可以为4,6,7,8部分,不能为5部分,
4.【答案】
D
【解析】
对于A,若
,可得
或
,A不符合题意;
对于B,若
,可得
或
,B不符合题意;
对于C,若
,则
,或
,或
与
相交,C不符合题意;
对于D,若
,则
,正确.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
