高二年级数学月考理科
图片预览


文档简介
2011--2012高二年级
第二学期理科数学月考试卷
班级: 姓名: 分数:
一.选择题:(每小题8分,共56分)
1.一直线运动的物体,从时间t到t+△t时,物体的位移为△s,那么为( B )
A.从时间t到t+△t时,物体的平均速度
B.时间t时该物体的瞬时速度
C.当时间为△t 时该物体的速度
D.从时间t到t+△t时位移的平均变化率
2.设f(x)在处可导,下列式子中与相等的是 ( B )
(1); (2);
(3) (4)。
A.(1)(2) B.(1)(3) C.(2)(3) D.(1)(2)(3)(4)
3. 设是函数的导函数,将和的图象画在同一个直角坐标系中,不可能正确的是( D )
4.在抛物线上依次取两点,它们的横坐标分别为,,若抛物线上过点P的切线与过这两点的割线平行,则P点的坐标为 ( D )
A. (3,9) B. (1,2) C. (1,1) D.(2,4)
5. 函数在处有极值10,则a、b的值为( A )
A. (4,-11) B. (-3,3) C. (4,-11)或(-3,3) D.(-4,5)或(3,-9)
6.点是曲线上任意一点,则点到直线的最小距离是( B )
A. B. C. D.
7.函数f(x)、g(x)在区间[a,b]上满足·g(x)>f(x)·
且g(x)>0,则对任意x(a,b)都有( C )
? A.f(x)·g(x)>f(a)·g(b) B.f(x)·g(x)>f(b)·g(b)
? C.f(x)·g(a)>f(a)·g(x) D.f(x)·g(b)>f(b)·g(x)
2011--2012高二年级
第二学期理科数学月考试卷
班级: 姓名: 分数:
一.选择题答题卡:(每小题8分,共56分)
题号 1 2 3 4 5 6 7
答案
二.填空题:(每小题8分,共24分)
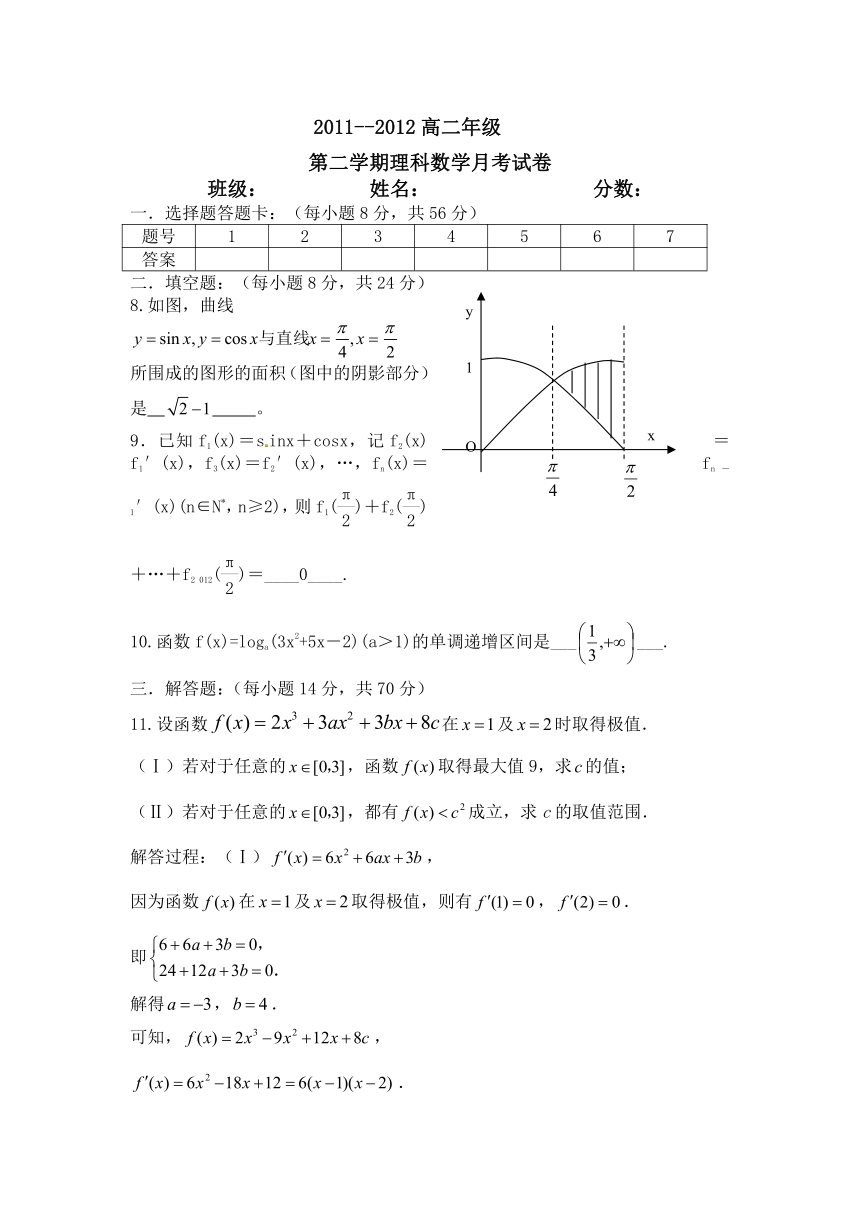
8.如图,曲线
所围成的图形的面积(图中的阴影部分)
是 。
9.已知f1(x)=sinx+cosx,记f2(x)=f1′(x),f3(x)=f2′(x),…,fn(x)=fn-1′(x)(n∈N*,n≥2),则f1()+f2()+…+f2 012()=____0____.
10.函数f(x)=loga(3x2+5x-2)(a>1)的单调递增区间是______.
三.解答题:(每小题14分,共70分)
11.设函数 ( http: / / www. / )在及 ( http: / / www. / )时取得极值.
(Ⅰ)若对于任意的,函数取得最大值9,求的值;
(Ⅱ)若对于任意的 ( http: / / www. / ),都有成立,求c的取值范围.
解答过程:(Ⅰ) ( http: / / www. / ),
因为函数在 ( http: / / www. / )及取得极值,则有 ( http: / / www. / ),.
即 ( http: / / www. / )
解得, ( http: / / www. / ).
可知,,
( http: / / www. / ).
当时, ( http: / / www. / );
当时, ( http: / / www. / );
当时, ( http: / / www. / ).
所以,当时, ( http: / / www. / )取得极大值,又 ( http: / / www. / ),.
则当 ( http: / / www. / )时,的最大值为 ( http: / / www. / ).所以
(Ⅱ)由(Ⅰ)可知,因为对于任意的,有 ( http: / / www. / )恒成立,
所以 ,
解得 ( http: / / www. / )或,
因此 ( http: / / www. / )的取值范围为.
12.已知曲线C1:y=x2与C2:y=-(x-2)2,直线l与C1、C2都相切,求直线l的方程.
12.解:设l与相切于点,与相切于。对,则与相切于点P的切线方程为,即。 ①
对,则与相切于点Q的切线方程为 ,即。 ②
∵ 两切线重合,∴,
解得或,
∴直线方程为y=0或y=4x-4。
13.求证方程在区间内有且仅有一个实根
13解:
在
∴ 在内与轴有且仅有一个交点
∴ 方程 在内仅有一解
14.如图,直线与轴所围成的图形分成了面积相等的两部分,求的值
14.解,
设曲线与直线相交与点,
,即交点为
把代入上式有:
15.求证下列不等式
(1)
15.证:(1)
∴ 为上 ∴ 恒成立
∴
∴ 在上 ∴ 恒成立
16.某商品每件成本9元,售价30元,每星期卖出432件.如果降低价格。销售量可以增加,且每星期多卖出的商品件数与商品单价的降价额度x(单位:元,)的平方成正比.已知商品单价降低2元时,一星期多卖出24件.
(Ⅰ)将一个星期的商品销售利润表示成x的函数;
(Ⅱ)如何定价才能使一个星期的商品销售利润最大?
16.解:(Ⅰ)设商品降价x元,则多卖的商品数为kx2,若记商品在一个星期的获利为f(x),则依题意有f(x)=(30-x-9)(432+kx2)=(21-x)(432+kx2).
又由已知条件,24=k·22,于是有k=6,
所以f(x)= -6x3+126x2-432x+9072,x∈[0,30].
(Ⅱ)根据(Ⅰ),我们有f′(x)=-18x2+252x-432=-18(x-2)(x-12).
X [0,2] 2 (2,12) 12 (12,30)
f′(x) - 0 + 0 -
f(x) 减函数 极小 增函数 极大 减函数
故x=12时,f(x)达到极大值,因为f(0)=9072、f(12)=11264,所以定价为30-12=18元能使一个星期的商品销售利润最大.
1
O
y
x
第二学期理科数学月考试卷
班级: 姓名: 分数:
一.选择题:(每小题8分,共56分)
1.一直线运动的物体,从时间t到t+△t时,物体的位移为△s,那么为( B )
A.从时间t到t+△t时,物体的平均速度
B.时间t时该物体的瞬时速度
C.当时间为△t 时该物体的速度
D.从时间t到t+△t时位移的平均变化率
2.设f(x)在处可导,下列式子中与相等的是 ( B )
(1); (2);
(3) (4)。
A.(1)(2) B.(1)(3) C.(2)(3) D.(1)(2)(3)(4)
3. 设是函数的导函数,将和的图象画在同一个直角坐标系中,不可能正确的是( D )
4.在抛物线上依次取两点,它们的横坐标分别为,,若抛物线上过点P的切线与过这两点的割线平行,则P点的坐标为 ( D )
A. (3,9) B. (1,2) C. (1,1) D.(2,4)
5. 函数在处有极值10,则a、b的值为( A )
A. (4,-11) B. (-3,3) C. (4,-11)或(-3,3) D.(-4,5)或(3,-9)
6.点是曲线上任意一点,则点到直线的最小距离是( B )
A. B. C. D.
7.函数f(x)、g(x)在区间[a,b]上满足·g(x)>f(x)·
且g(x)>0,则对任意x(a,b)都有( C )
? A.f(x)·g(x)>f(a)·g(b) B.f(x)·g(x)>f(b)·g(b)
? C.f(x)·g(a)>f(a)·g(x) D.f(x)·g(b)>f(b)·g(x)
2011--2012高二年级
第二学期理科数学月考试卷
班级: 姓名: 分数:
一.选择题答题卡:(每小题8分,共56分)
题号 1 2 3 4 5 6 7
答案
二.填空题:(每小题8分,共24分)
8.如图,曲线
所围成的图形的面积(图中的阴影部分)
是 。
9.已知f1(x)=sinx+cosx,记f2(x)=f1′(x),f3(x)=f2′(x),…,fn(x)=fn-1′(x)(n∈N*,n≥2),则f1()+f2()+…+f2 012()=____0____.
10.函数f(x)=loga(3x2+5x-2)(a>1)的单调递增区间是______.
三.解答题:(每小题14分,共70分)
11.设函数 ( http: / / www. / )在及 ( http: / / www. / )时取得极值.
(Ⅰ)若对于任意的,函数取得最大值9,求的值;
(Ⅱ)若对于任意的 ( http: / / www. / ),都有成立,求c的取值范围.
解答过程:(Ⅰ) ( http: / / www. / ),
因为函数在 ( http: / / www. / )及取得极值,则有 ( http: / / www. / ),.
即 ( http: / / www. / )
解得, ( http: / / www. / ).
可知,,
( http: / / www. / ).
当时, ( http: / / www. / );
当时, ( http: / / www. / );
当时, ( http: / / www. / ).
所以,当时, ( http: / / www. / )取得极大值,又 ( http: / / www. / ),.
则当 ( http: / / www. / )时,的最大值为 ( http: / / www. / ).所以
(Ⅱ)由(Ⅰ)可知,因为对于任意的,有 ( http: / / www. / )恒成立,
所以 ,
解得 ( http: / / www. / )或,
因此 ( http: / / www. / )的取值范围为.
12.已知曲线C1:y=x2与C2:y=-(x-2)2,直线l与C1、C2都相切,求直线l的方程.
12.解:设l与相切于点,与相切于。对,则与相切于点P的切线方程为,即。 ①
对,则与相切于点Q的切线方程为 ,即。 ②
∵ 两切线重合,∴,
解得或,
∴直线方程为y=0或y=4x-4。
13.求证方程在区间内有且仅有一个实根
13解:
在
∴ 在内与轴有且仅有一个交点
∴ 方程 在内仅有一解
14.如图,直线与轴所围成的图形分成了面积相等的两部分,求的值
14.解,
设曲线与直线相交与点,
,即交点为
把代入上式有:
15.求证下列不等式
(1)
15.证:(1)
∴ 为上 ∴ 恒成立
∴
∴ 在上 ∴ 恒成立
16.某商品每件成本9元,售价30元,每星期卖出432件.如果降低价格。销售量可以增加,且每星期多卖出的商品件数与商品单价的降价额度x(单位:元,)的平方成正比.已知商品单价降低2元时,一星期多卖出24件.
(Ⅰ)将一个星期的商品销售利润表示成x的函数;
(Ⅱ)如何定价才能使一个星期的商品销售利润最大?
16.解:(Ⅰ)设商品降价x元,则多卖的商品数为kx2,若记商品在一个星期的获利为f(x),则依题意有f(x)=(30-x-9)(432+kx2)=(21-x)(432+kx2).
又由已知条件,24=k·22,于是有k=6,
所以f(x)= -6x3+126x2-432x+9072,x∈[0,30].
(Ⅱ)根据(Ⅰ),我们有f′(x)=-18x2+252x-432=-18(x-2)(x-12).
X [0,2] 2 (2,12) 12 (12,30)
f′(x) - 0 + 0 -
f(x) 减函数 极小 增函数 极大 减函数
故x=12时,f(x)达到极大值,因为f(0)=9072、f(12)=11264,所以定价为30-12=18元能使一个星期的商品销售利润最大.
1
O
y
x
