浙江省杭州市西湖高级中学2012届高三3月月考数学(文)试题
文档属性
| 名称 | 浙江省杭州市西湖高级中学2012届高三3月月考数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 426.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-22 15:21:48 | ||
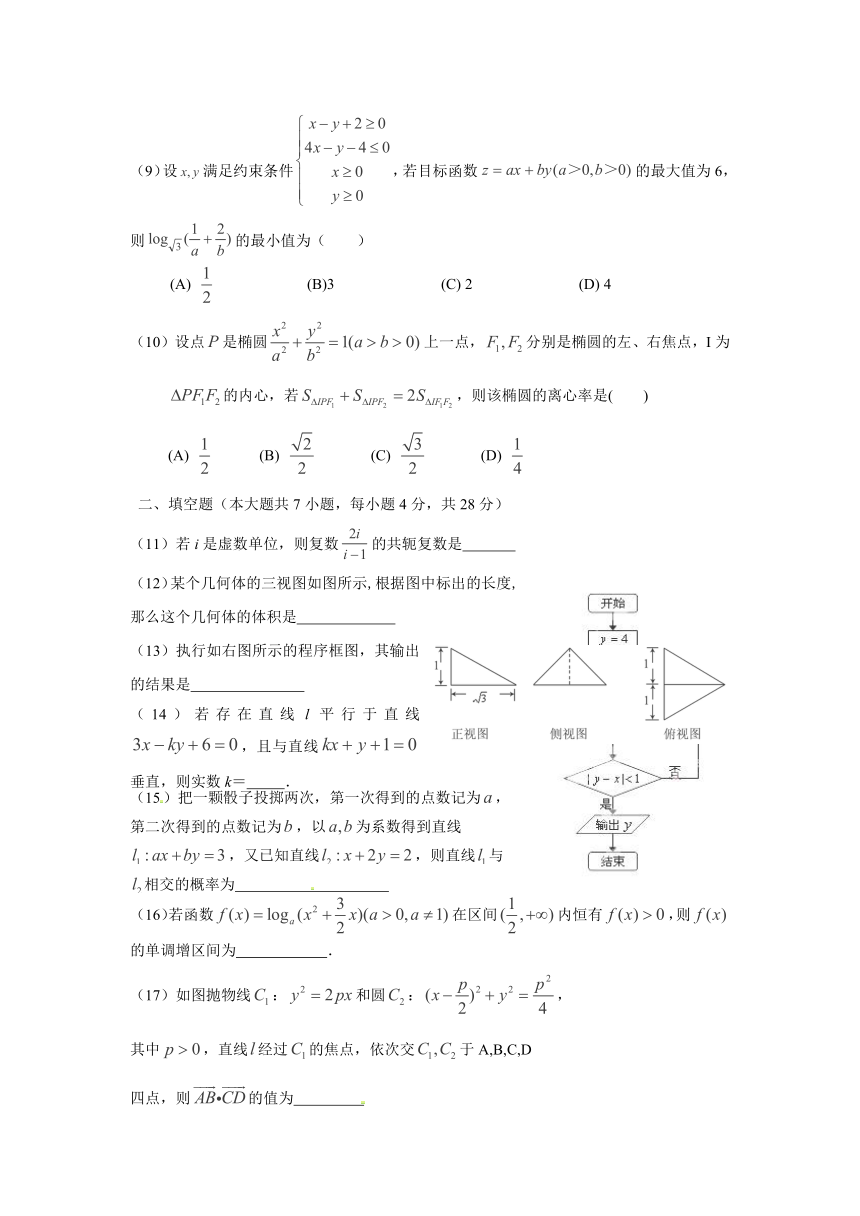
图片预览



文档简介
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
(1)若全集 U=R,集合,,则集合( )
(A) (B) (C) (D)
(2)已知函数,则= ( )
(A) 3 (B) 8 (C) 9 (D) 12
(3)已知数列的前n项和,若,则n的值等于( )
(A) 5 (B) 4 (C) 3 (D) 2
(4)设a,b,c表示三条直线, 表示两个平面,则下列命题中逆命题不成立的是( )
(A),若,则 (B) ,若,则
(C),若,则
(D) ,若,则
(5)已知点在圆上,点在直线上上,若的最小值为,则= ( )
(A) 1 (B) (C) 0 (D) 2
(6)函数在内有极小值,则实数的取值范围为( )
(A) (B) (C) (D)
(7)已知,则( )
(A) (B) (C) (D)
(8)已知平面内的向量满足:, ,且,又,,则满足条件点P所表示的图形面积是( )
(A) 8 (B) 4 (C) 2 (D) 1
(9)设满足约束条件,若目标函数的最大值为6,则的最小值为( )
(A) (B)3 (C) 2 (D) 4
(10)设点是椭圆上一点,分别是椭圆的左、右焦点,I为的内心,若,则该椭圆的离心率是( )
(A) (B) (C) (D)
二、填空题(本大题共7小题,每小题4分,共28分)
(11)若i是虚数单位,则复数的共轭复数是
(12)某个几何体的三视图如图所示,根据图中标出的长度,那么这个几何体的体积是
(13)执行如右图所示的程序框图,其输出的结果是
(14)若存在直线l平行于直线,且与直线垂直,则实数k= .
(15)把一颗骰子投掷两次,第一次得到的点数记为,
第二次得到的点数记为,以为系数得到直线
,又已知直线,则直线与
相交的概率为
(16)若函数在区间内恒有,则的单调增区间为 .
(17)如图抛物线:和圆:,
其中,直线经过的焦点,依次交于A,B,C,D
四点,则的值为
三、解答题:(本大题共5小题,共72分,解答应写出文字说明、证明过程或演算步骤.)
18. (本题满分14分)已知向量 与 共线,设函数。
(1)求函数的周期及最大值;
(2)已知锐角 △ABC 中的三个内角分别为 A、B、C,若有,边 BC=,,求 △ABC 的面积.
19. (本题满分14分)如图,AC 是圆 O 的直径,点 B 在圆 O 上,,交 AC 于点 M,平面,,AC=4,EA=3,FC=1.
(I)证明:EM⊥BF;
(II)求平面 BEF 与平面ABC 所成的二面角的余弦值.
20.(本题满分14分)已知数列中,,,(1)求证:数列为等比数列。
(2)设数列的前项和为,若,求正整数列的最小值。
21.(本题满分15分) 已知函数是奇函数,是偶函数,设.
(1)若,令函数,求函数在上的极值;
(2)对恒有成立,求实数的取值范围.
22.(本题满分15分) 已知抛物线的焦点为F,抛物线上一点A的横坐标为,过点A作抛物线C的切线交轴于点D,交轴于点Q,交直线于点M,当时,.
(Ⅰ)求证:为等腰三角形,并求抛物线C的方程;
(Ⅱ)若B位于轴左侧的抛物线C上,过点B作抛物线C的切线交直线于点P,交直线于点N,求面积的最小值,并求取到最小值时的值.
杭西高2012年3月高三文科数学答案
选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
三、解答题:本大题共5小题,共72分,解答应写出文字说明、证明过程或演算步骤.
18.(1)因为,所以
(2)
┄┄┄┄┄┄┄┄14分
,即(也可由勾股定理证得).
, 平面.
而平面,
. ………………………………………………………………………………6分
(2)延长交于,连,过作,连结.
由(1)知平面,平面,
.
而,平面.
平面,
,
为平面与平面所成的
二面角的平面角. ……………………8分
在中,,,
.
由,得.
,则.
是等腰直角三角形,.
平面与平面所成的锐二面角的余弦值为. ………………………14分
20.因为
所以
所以数列为等比数列。
(2)
可知时满足条件。
21. 因为函数是奇函数,是偶函数,故.(2分)
(1)时,,,所以
递减 递增 递减
由得或(5分 )
∴函数在处取得极小值;在处取得极大值(7分)
(2)的对称轴为,对恒有,所以函数在上恒为单调递增函数.①若即时,要使函数在上恒为单调递增函数,则有,解得:,所以;(10分)②若即时,要使函数在上恒为单调递增函数,则有,解得:;(13分)综上,实数a的取值范围为(15分)
(1)若全集 U=R,集合,,则集合( )
(A) (B) (C) (D)
(2)已知函数,则= ( )
(A) 3 (B) 8 (C) 9 (D) 12
(3)已知数列的前n项和,若,则n的值等于( )
(A) 5 (B) 4 (C) 3 (D) 2
(4)设a,b,c表示三条直线, 表示两个平面,则下列命题中逆命题不成立的是( )
(A),若,则 (B) ,若,则
(C),若,则
(D) ,若,则
(5)已知点在圆上,点在直线上上,若的最小值为,则= ( )
(A) 1 (B) (C) 0 (D) 2
(6)函数在内有极小值,则实数的取值范围为( )
(A) (B) (C) (D)
(7)已知,则( )
(A) (B) (C) (D)
(8)已知平面内的向量满足:, ,且,又,,则满足条件点P所表示的图形面积是( )
(A) 8 (B) 4 (C) 2 (D) 1
(9)设满足约束条件,若目标函数的最大值为6,则的最小值为( )
(A) (B)3 (C) 2 (D) 4
(10)设点是椭圆上一点,分别是椭圆的左、右焦点,I为的内心,若,则该椭圆的离心率是( )
(A) (B) (C) (D)
二、填空题(本大题共7小题,每小题4分,共28分)
(11)若i是虚数单位,则复数的共轭复数是
(12)某个几何体的三视图如图所示,根据图中标出的长度,那么这个几何体的体积是
(13)执行如右图所示的程序框图,其输出的结果是
(14)若存在直线l平行于直线,且与直线垂直,则实数k= .
(15)把一颗骰子投掷两次,第一次得到的点数记为,
第二次得到的点数记为,以为系数得到直线
,又已知直线,则直线与
相交的概率为
(16)若函数在区间内恒有,则的单调增区间为 .
(17)如图抛物线:和圆:,
其中,直线经过的焦点,依次交于A,B,C,D
四点,则的值为
三、解答题:(本大题共5小题,共72分,解答应写出文字说明、证明过程或演算步骤.)
18. (本题满分14分)已知向量 与 共线,设函数。
(1)求函数的周期及最大值;
(2)已知锐角 △ABC 中的三个内角分别为 A、B、C,若有,边 BC=,,求 △ABC 的面积.
19. (本题满分14分)如图,AC 是圆 O 的直径,点 B 在圆 O 上,,交 AC 于点 M,平面,,AC=4,EA=3,FC=1.
(I)证明:EM⊥BF;
(II)求平面 BEF 与平面ABC 所成的二面角的余弦值.
20.(本题满分14分)已知数列中,,,(1)求证:数列为等比数列。
(2)设数列的前项和为,若,求正整数列的最小值。
21.(本题满分15分) 已知函数是奇函数,是偶函数,设.
(1)若,令函数,求函数在上的极值;
(2)对恒有成立,求实数的取值范围.
22.(本题满分15分) 已知抛物线的焦点为F,抛物线上一点A的横坐标为,过点A作抛物线C的切线交轴于点D,交轴于点Q,交直线于点M,当时,.
(Ⅰ)求证:为等腰三角形,并求抛物线C的方程;
(Ⅱ)若B位于轴左侧的抛物线C上,过点B作抛物线C的切线交直线于点P,交直线于点N,求面积的最小值,并求取到最小值时的值.
杭西高2012年3月高三文科数学答案
选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
三、解答题:本大题共5小题,共72分,解答应写出文字说明、证明过程或演算步骤.
18.(1)因为,所以
(2)
┄┄┄┄┄┄┄┄14分
,即(也可由勾股定理证得).
, 平面.
而平面,
. ………………………………………………………………………………6分
(2)延长交于,连,过作,连结.
由(1)知平面,平面,
.
而,平面.
平面,
,
为平面与平面所成的
二面角的平面角. ……………………8分
在中,,,
.
由,得.
,则.
是等腰直角三角形,.
平面与平面所成的锐二面角的余弦值为. ………………………14分
20.因为
所以
所以数列为等比数列。
(2)
可知时满足条件。
21. 因为函数是奇函数,是偶函数,故.(2分)
(1)时,,,所以
递减 递增 递减
由得或(5分 )
∴函数在处取得极小值;在处取得极大值(7分)
(2)的对称轴为,对恒有,所以函数在上恒为单调递增函数.①若即时,要使函数在上恒为单调递增函数,则有,解得:,所以;(10分)②若即时,要使函数在上恒为单调递增函数,则有,解得:;(13分)综上,实数a的取值范围为(15分)
同课章节目录
