六年级数学下册试题 一课一练《正比例和反比例》习题1-苏教版(含答案)
文档属性
| 名称 | 六年级数学下册试题 一课一练《正比例和反比例》习题1-苏教版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 713.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-18 10:31:02 | ||
图片预览



文档简介
《正比例和反比例》习题1
一、选择题
1.下面各题中的两个量成正比例的是
A.圆柱的体积一定,圆柱的底面积和高
B.稻谷每公顷产量一定,稻谷的总产量和公顷数
C.一个人的身高和他的年龄
D.在一块菜地上种的黄瓜与西红柿的面积
2.下列各项中,两种量成反比例关系的是
A.工作效率一定,工作时间与工作总量
B.人的年龄与其身高
C.长方形的周长一定,它的长与宽
D.三角形的面积一定,这个三角形的底和高
3.用一定的钱买地砖,每块砖的价钱和买砖块数
A.成正比例
B.成反比例
C.不成比例
D.不成反比例
4.有1桶油,如果每天吃100克,能吃50天;如果每天吃200克,能吃25天.每天的吃油量(单位:克)与所吃的时间(单位:天)
A.成正比例
B.不成比例
C.成反比例
5.下面题中的两种量成不成比例,成什么比例. 同时同地,物体的高度和影长.
A.成正比例
B.成反比例
C.不成比例
6.汽车从北京到上海,所用的时间和速度
A.成正比例
B.成反比例
C.不成比例
7.做一批零件用的时间一定,每个零件所需时间和零件的个数是
A.正比例
B.反比例
C.不成比例
二、填空题
1.因为:
路程(一定),所以
和
成
比例.
2.下面相关联的两个量中, 成正比例, 成反比例.
.淘气步行从家到学校,所用的时间和平均速度;
.淘气步行从家
到学校,已走的路程和未走的路程;
.每张邮票1.2元,淘气买邮票应付的钱数
和所买的邮票张数;
.圆的面积和半径.
3.选一选
.成正比例
.不成比例
①一条路的总长度一定,已修的长度和未修的长度 ;
②《小学生数学报》单价一定,订阅份数和总价 .
4.601班同学排队做操,排成的列数和每列人数成 比例;实际距离一定,图上距离和比例尺成 比例.
5.表中和是两种相关联的量,并且成正比例关系,你能将表填写完整吗?
6
8
21
24
30
6.看表填空.
与
.、成正比例
、成反比例
2
3
5
10
4.5
7.5
12
三、判断题
1.修一条路,已修的与未修的长度成反比例关系.(
)
2.书的总页数一定,已读页数与剩下页数成反比例.(
)
3.圆的面积与半径成正比例关系.(
)
4.长方形的长一定,面积与宽成正比例,周长与宽成反比例.(
)
5.路程和速度成正比例.(
)
6.如果,则与成反比例(
)
7.如果,那么与成正比例.(
)
四、解答题
1.
时间时
1
2
3
4
5
6
路程千米
90
①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
②时间和路程成 比例,理由是 .
③利用图象估计一下,2.5时行 千米,行675千米需要 小时.
2.汽车数量与运货质量的数据如下表,根据表中的数据回答下面各题.
汽车数量辆
1
2
3
4
5
6
7
运货质量吨
4
8
12
16
20
24
28
(1)表中 和 是两种相关联的量, 随着 的变化而变化.
(2)写出几组这两种量中相对应的两个数的比,求出比值,并比较比值的大小.
(3)上面求出的比值表示的意义是什么?
(4)表中相关联的两种量成正比例吗?为什么?
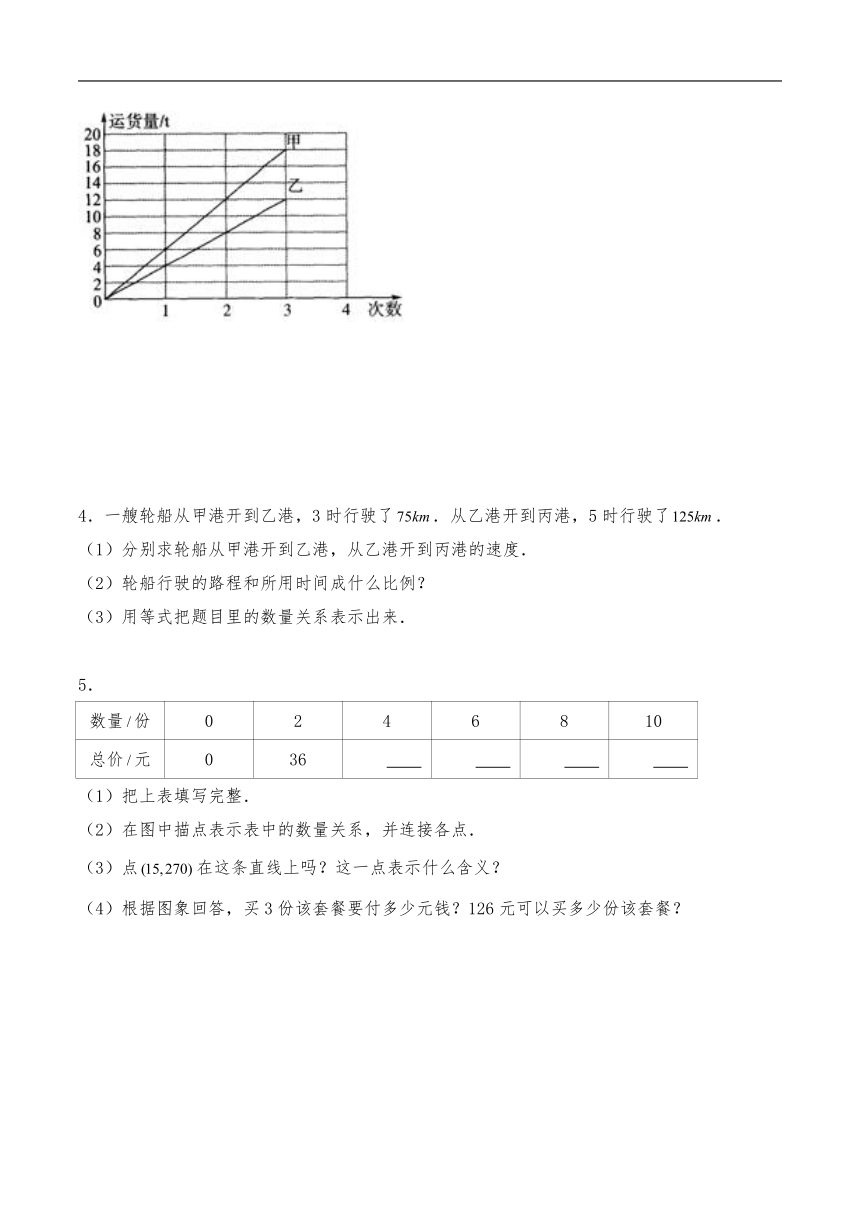
3.如图,甲、乙两车运货的吨数与次数的关系如图.
(1)甲车的运货量与运货次数成什么比例关系?乙车呢?
(2)甲、乙两车各运货6次,运货量相差多少吨?
4.一艘轮船从甲港开到乙港,3时行驶了.从乙港开到丙港,5时行驶了.
(1)分别求轮船从甲港开到乙港,从乙港开到丙港的速度.
(2)轮船行驶的路程和所用时间成什么比例?
(3)用等式把题目里的数量关系表示出来.
5.
数量份
0
2
4
6
8
10
总价元
0
36
(1)把上表填写完整.
(2)在图中描点表示表中的数量关系,并连接各点.
(3)点在这条直线上吗?这一点表示什么含义?
(4)根据图象回答,买3份该套餐要付多少元钱?126元可以买多少份该套餐?
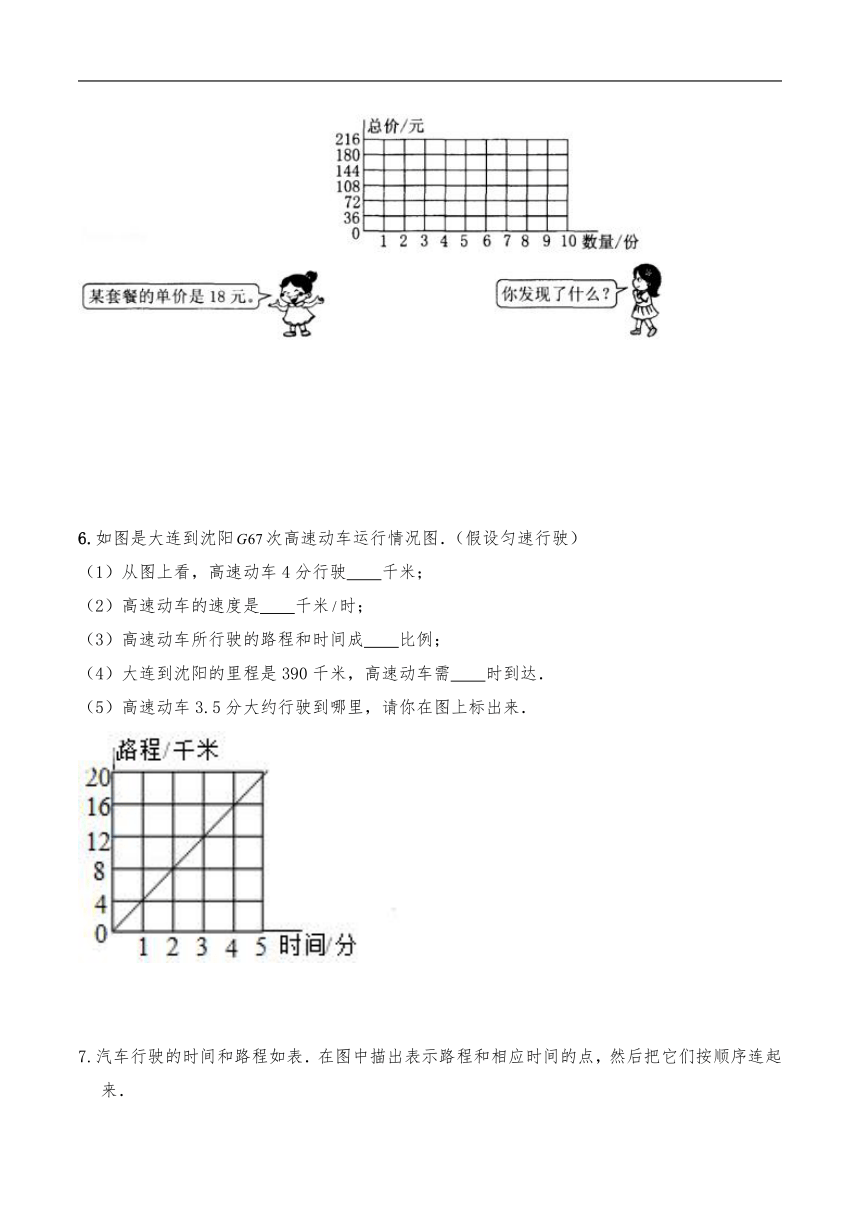
6.如图是大连到沈阳次高速动车运行情况图.(假设匀速行驶)
(1)从图上看,高速动车4分行驶 千米;
(2)高速动车的速度是 千米时;
(3)高速动车所行驶的路程和时间成 比例;
(4)大连到沈阳的里程是390千米,高速动车需 时到达.
(5)高速动车3.5分大约行驶到哪里,请你在图上标出来.
7.汽车行驶的时间和路程如表.在图中描出表示路程和相应时间的点,然后把它们按顺序连起来.
时间时
1
2
3
4
5
6
路程
80
160
240
320
400
480
8.长沙造纸厂的生产情况如下表,根据表回答问题.
时间(天
1
2
3
4
5
6
7
生产量(吨
70
140
210
280
350
420
490
(1)表中相关联的量是
和
.
(2)根据表中的数据,写出一个比例
.
(3)表中相关联的两种量成
关系.
(4)在图中描出表示时间和相应生产量的点,并把它们按顺序连接起来.
(5)估计生产550吨纸片,大约需要
天(填整数).
9.在同一地点、同一时间测得的不同物体的高度和它的影长如下表,请你把这两个量的变化情况画在图中.
物体高度米
1
2
3
4
影长米
0.6
12
1.8
2.4
10.如图图象表示长颈鹿的奔跑情况,请回答下面问题:
(1)完成表:
时间分
5
10
15
20
25
30
路程千米
(2)不计算,根据图象估计一下,长颈鹿跑,大约要
分钟.
(3)长颈鹿奔跑的路程和时间是否成比例?成什么比例?
.
11.下面是同一时间、同一地点,测量的杆高和影长的记录表.根据表中的记录,杆高和影
长是否成正比例?如果成正比例的话,在如图的图象中表示出来.
杆高(米
1.5
3
4.5
6
影长(米
1
2
3
4
12.选一根粗细均匀的竹竿:(长约,在中点的位置打个小孔并拴上绳子,然后每隔做一个刻度.
(1)如果塑料袋挂在竹竿左右两边刻度相同的地方,左边放5个棋子,右边应放 个棋子才能保证竹竿平衡.
(2)如果右边的塑料袋放10个棋子,放在刻度3上,左边的塑料袋放在刻度5上,应该放 个棋子才能保证平衡.
为了保证平衡,左边还可以怎么放?找出规律,填写下表.
左边刻度
1
2
3
6
所放棋子数
乘积
(3)从表中你发现刻度数与所放棋子数成什么比例关系?
13.下面的图象表示实验小学食堂的用煤天数和用煤量的关系.
(1)根据图象,你能判断用煤天数和用煤量成什么比例吗?
(2)如果用表示用煤的数,表示用煤的天数,表示每天的用煤量,它们之间的关系可以表示为 .
(3)根据图象判断,5天要用煤多少吨?2.4吨煤可用多少天?
14.用,分别表示面积为96平方厘米的平行四边形的底和高,请完成下表,并回答问题.
1
2
3
4
6
8
12
24
48
96
(1)随着的增加是怎样变化的?
(2)与成什么关系?为什么?
(3)当平行四边形的底为15厘米时,高是多少厘米?
15.王叔叔买了一辆汽车,下表是他在试车过程中记录下的数据.
汽车所行路程
0
15
30
45
60
耗油量
0
2
4
6
8
(1)汽车所行路程与耗油量有什么关系?
(2)汽车行驶,耗油多少升?
(3)当油箱还剩油时,汽车还能行驶多少千米?
16.同一时间、同一地点测得树高和影长的数据如表:
树高
2
3
4
6
影长
1.6
2.4
3.2
4.8
(1)在图中描出表示树高和对应影长的点,然后把它们连起来.
(2)连线以后观察,它们是在一条直线上吗?
,说明树高和影长成
关系.
(3)不计算,利用图象判断,树高8米时,影长
米?影长4米时,树高
米?
17.食堂每天开饭人数与购买蔬菜的数量如表:
每天开饭人数个
0
1
2
3
4
5
6
7
8
购买蔬菜的数量千克
0
0.5
1
1.5
2
(1)根据已知的数量关系补充完整上面的表格.
(2)根据表中的数在下面图中描出对应的点,再把各个点连接起来.
(3)上面的两种量成比例吗?如果成,成什么比例,为什么?
答案
一、选择题
1.2..3..4..5..6..7..
二、填空题
1.速度,时间,速度,时间,反.
2.:,.
3.;.
4.:反,正.
5.18、7、9、27、10.
6..
三、判断题
1..2..3..4..5..6..7.
四、解答题
1.解:①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
时间时
1
2
3
4
5
6
路程千米
90
180
270
360
450
540
②时间和路程成
正比例,理由是
路程时间速度(一定).
③如图
用图象估计一下,2.5时行
225千米,行675千米需要
7.5小时.
故答案为:正,路程时间速度(一定),225,7.5.
2.解:(1)表中有汽车数量和运货质量两种量,它们是两种相关联的量,一个量变大,另一个量也随着变大,它们的比值一定,所以汽车数量和运货质量成正比例关系.
(2),,,,它们的比值相等.
(3)根据题意可知,这个比值表示每辆汽车的运货质量.
(4)相关联的两种量成正比例,因为它们的比值一定.
故答案为:汽车数量;运货质量;运货质量;汽车数量.
3.解:(1)甲:(一定),是比值一定,所以甲车的运货量与运货次数成正比例关系.
乙:(一定),是比值一定,所以乙车的运货量与运货次数成正比例关系.
(2)
(吨
(吨
答:甲、乙两车各运货6次,运货量相差12吨.
4.解:从甲港开到乙港的速度:(千米时).
从乙港开到丙港的速度:(千米时).
答:轮船从甲港开到乙港,从乙港开到丙港的速度都是25千米时.
(2)由(1)可知(一定),是比值一定,所以轮船行驶的路程和所用时间成正比例.
(3)设表示路程,表示时间,表示速度,则等量关系为:.
5.解:
数量份
0
2
4
6
8
10
总价元
0
36
72
108
144
180
(1)总价与质量成正比例.
(2)根据表格中数据可在右图中描点连线,得出统计图如图:
(3)点在这条直线上,这一点表示15份套餐需要270元钱.
(4)(元),
(份),
答:买3份该套餐要付54元钱,126元可以买7份该套餐.
6.解:(1)答:高速动车4分钟行驶16千米.
(2)(千米时);
答:高速动车的速度是240千米时.
(3)因为速度(一定),所以高速动车所行驶的路程和时间成正比例.
(4)(小时);
答:高速动车需要1.625小时.
(5)(千米);
故答案为:16;4;正;1.625.
7.解:如图:
8.解:(1)表中相关联的量是时间(天)和生产量(吨).
(2)根据表中的数据,写出一个比例:(答案不唯一).
(3)表中相关联的两种量成正比例关系.
(4)在图中描出表示时间和相应生产量的点,并把它们按顺序连接起来(下图).
(5)估计生产550吨纸片,大约需要8天(填整数)(下图红色虚线与横轴的交点).
故答案为:时间(天),生产量(吨),(答案不唯一),正比例,8.
9.解:
10.解:(1)
时间分
5
10
15
20
25
30
路程千米
4
8
12
16
20
24
(2)不计算,根据图象估计一下,长颈鹿跑,大约要12.5分钟.
(3)长颈鹿奔跑的路程和时间是成比例;成正比例.
故答案为:12.5,正,
11.解:(1)(一定),
因为每米高影长的物体(一定),所以杆高和它的影长成正比例;
(2)绘制统计图如下图,观察发现:表示树高和对应影长的点,都在一条直线上;
12.解:(1)如果塑料袋挂在竹竿左右两边刻度相同的地方,左边放5个棋子,右边应放5个棋子才能保持保证竹竿平衡.
(2)设左边应放个棋子才能保证平衡,
答:应该放6个棋子才能保证平衡.
同理:
;
;
;
.
为了保证平衡,左边还可以怎么放?找出规律,填写下表.
左边刻度
1
2
3
6
所放棋子数
30
15
10
5
乘积
(3)因为动力动力臂阻力阻力臂,也就是积一定,所以发现刻度数与所放棋子数成反比例关系.
故答案为:5;6;
13.解:(1)用煤的吨数用煤的天数每天的用煤量(一定)
根据两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就是成正比例的量
因此可判断用煤天数和用煤量成正比例关系.
(2)如果用表示用煤的数,表示用煤的天数,表示每天的用煤量,它们之间的关系可以表示为(一定).
(3)根据图象可判断:5天有煤1.5吨;2.4吨煤可以用8天.
故答案为:(一定).
14.解:(1)(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
填表如下:
1
2
3
4
6
8
12
24
48
96
48
32
24
16
12
8
4
2
(1)随着的增加而减少.
(2)因为底高平行四边形的面积(一定),所以平行四边形底和高成反比例.
(3)设高为厘米,
.
答:高是6.4厘米.
15.解:(1)耗油量随着路程的变化而变化,因为、即每升油所行路程不变,所以汽车所行路程和耗油量成正比例关系;
(2)因为耗油量路程每升油所行路程,
升)
答:要耗油12升.
(3)因为路程每升油所行路程耗油量,
(千米)
答:汽车大约还能行驶22.5千米.
16.解:(1)所作图象如下图,观察发现:表示树高和对应影长的点,都在一条直线上.
(2)连线以后,发现表示树高和对应影长的点,都在一条直线上,这说明树高和影长成正比例关系,
因为随着树的高度的增加,影长也在增加,且树高与影长的商是一定的,所以树高和影长成正比例关系;
(3)设树高8时,影长为米,影长时,树高米,
则有
;
答:树高时,影长6.4米,影长时,树高5米.
故答案为:在、正比例;
6.4,5.
17.解:(1)食堂每天开饭人数与购买蔬菜的数量如下表:
每天开饭人数个
0
1
2
3
4
5
6
7
8
购买蔬菜的数量千克
0
0.5
1
1.5
2
2.5
3
3.5
4
(2)作图如下:
(3)因为(一定),所以购买蔬菜的数量和人数成正比例关系.
答:成比例;因为(一定),所以购买蔬菜的数量和人数成正比例关系.
一、选择题
1.下面各题中的两个量成正比例的是
A.圆柱的体积一定,圆柱的底面积和高
B.稻谷每公顷产量一定,稻谷的总产量和公顷数
C.一个人的身高和他的年龄
D.在一块菜地上种的黄瓜与西红柿的面积
2.下列各项中,两种量成反比例关系的是
A.工作效率一定,工作时间与工作总量
B.人的年龄与其身高
C.长方形的周长一定,它的长与宽
D.三角形的面积一定,这个三角形的底和高
3.用一定的钱买地砖,每块砖的价钱和买砖块数
A.成正比例
B.成反比例
C.不成比例
D.不成反比例
4.有1桶油,如果每天吃100克,能吃50天;如果每天吃200克,能吃25天.每天的吃油量(单位:克)与所吃的时间(单位:天)
A.成正比例
B.不成比例
C.成反比例
5.下面题中的两种量成不成比例,成什么比例. 同时同地,物体的高度和影长.
A.成正比例
B.成反比例
C.不成比例
6.汽车从北京到上海,所用的时间和速度
A.成正比例
B.成反比例
C.不成比例
7.做一批零件用的时间一定,每个零件所需时间和零件的个数是
A.正比例
B.反比例
C.不成比例
二、填空题
1.因为:
路程(一定),所以
和
成
比例.
2.下面相关联的两个量中, 成正比例, 成反比例.
.淘气步行从家到学校,所用的时间和平均速度;
.淘气步行从家
到学校,已走的路程和未走的路程;
.每张邮票1.2元,淘气买邮票应付的钱数
和所买的邮票张数;
.圆的面积和半径.
3.选一选
.成正比例
.不成比例
①一条路的总长度一定,已修的长度和未修的长度 ;
②《小学生数学报》单价一定,订阅份数和总价 .
4.601班同学排队做操,排成的列数和每列人数成 比例;实际距离一定,图上距离和比例尺成 比例.
5.表中和是两种相关联的量,并且成正比例关系,你能将表填写完整吗?
6
8
21
24
30
6.看表填空.
与
.、成正比例
、成反比例
2
3
5
10
4.5
7.5
12
三、判断题
1.修一条路,已修的与未修的长度成反比例关系.(
)
2.书的总页数一定,已读页数与剩下页数成反比例.(
)
3.圆的面积与半径成正比例关系.(
)
4.长方形的长一定,面积与宽成正比例,周长与宽成反比例.(
)
5.路程和速度成正比例.(
)
6.如果,则与成反比例(
)
7.如果,那么与成正比例.(
)
四、解答题
1.
时间时
1
2
3
4
5
6
路程千米
90
①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
②时间和路程成 比例,理由是 .
③利用图象估计一下,2.5时行 千米,行675千米需要 小时.
2.汽车数量与运货质量的数据如下表,根据表中的数据回答下面各题.
汽车数量辆
1
2
3
4
5
6
7
运货质量吨
4
8
12
16
20
24
28
(1)表中 和 是两种相关联的量, 随着 的变化而变化.
(2)写出几组这两种量中相对应的两个数的比,求出比值,并比较比值的大小.
(3)上面求出的比值表示的意义是什么?
(4)表中相关联的两种量成正比例吗?为什么?
3.如图,甲、乙两车运货的吨数与次数的关系如图.
(1)甲车的运货量与运货次数成什么比例关系?乙车呢?
(2)甲、乙两车各运货6次,运货量相差多少吨?
4.一艘轮船从甲港开到乙港,3时行驶了.从乙港开到丙港,5时行驶了.
(1)分别求轮船从甲港开到乙港,从乙港开到丙港的速度.
(2)轮船行驶的路程和所用时间成什么比例?
(3)用等式把题目里的数量关系表示出来.
5.
数量份
0
2
4
6
8
10
总价元
0
36
(1)把上表填写完整.
(2)在图中描点表示表中的数量关系,并连接各点.
(3)点在这条直线上吗?这一点表示什么含义?
(4)根据图象回答,买3份该套餐要付多少元钱?126元可以买多少份该套餐?
6.如图是大连到沈阳次高速动车运行情况图.(假设匀速行驶)
(1)从图上看,高速动车4分行驶 千米;
(2)高速动车的速度是 千米时;
(3)高速动车所行驶的路程和时间成 比例;
(4)大连到沈阳的里程是390千米,高速动车需 时到达.
(5)高速动车3.5分大约行驶到哪里,请你在图上标出来.
7.汽车行驶的时间和路程如表.在图中描出表示路程和相应时间的点,然后把它们按顺序连起来.
时间时
1
2
3
4
5
6
路程
80
160
240
320
400
480
8.长沙造纸厂的生产情况如下表,根据表回答问题.
时间(天
1
2
3
4
5
6
7
生产量(吨
70
140
210
280
350
420
490
(1)表中相关联的量是
和
.
(2)根据表中的数据,写出一个比例
.
(3)表中相关联的两种量成
关系.
(4)在图中描出表示时间和相应生产量的点,并把它们按顺序连接起来.
(5)估计生产550吨纸片,大约需要
天(填整数).
9.在同一地点、同一时间测得的不同物体的高度和它的影长如下表,请你把这两个量的变化情况画在图中.
物体高度米
1
2
3
4
影长米
0.6
12
1.8
2.4
10.如图图象表示长颈鹿的奔跑情况,请回答下面问题:
(1)完成表:
时间分
5
10
15
20
25
30
路程千米
(2)不计算,根据图象估计一下,长颈鹿跑,大约要
分钟.
(3)长颈鹿奔跑的路程和时间是否成比例?成什么比例?
.
11.下面是同一时间、同一地点,测量的杆高和影长的记录表.根据表中的记录,杆高和影
长是否成正比例?如果成正比例的话,在如图的图象中表示出来.
杆高(米
1.5
3
4.5
6
影长(米
1
2
3
4
12.选一根粗细均匀的竹竿:(长约,在中点的位置打个小孔并拴上绳子,然后每隔做一个刻度.
(1)如果塑料袋挂在竹竿左右两边刻度相同的地方,左边放5个棋子,右边应放 个棋子才能保证竹竿平衡.
(2)如果右边的塑料袋放10个棋子,放在刻度3上,左边的塑料袋放在刻度5上,应该放 个棋子才能保证平衡.
为了保证平衡,左边还可以怎么放?找出规律,填写下表.
左边刻度
1
2
3
6
所放棋子数
乘积
(3)从表中你发现刻度数与所放棋子数成什么比例关系?
13.下面的图象表示实验小学食堂的用煤天数和用煤量的关系.
(1)根据图象,你能判断用煤天数和用煤量成什么比例吗?
(2)如果用表示用煤的数,表示用煤的天数,表示每天的用煤量,它们之间的关系可以表示为 .
(3)根据图象判断,5天要用煤多少吨?2.4吨煤可用多少天?
14.用,分别表示面积为96平方厘米的平行四边形的底和高,请完成下表,并回答问题.
1
2
3
4
6
8
12
24
48
96
(1)随着的增加是怎样变化的?
(2)与成什么关系?为什么?
(3)当平行四边形的底为15厘米时,高是多少厘米?
15.王叔叔买了一辆汽车,下表是他在试车过程中记录下的数据.
汽车所行路程
0
15
30
45
60
耗油量
0
2
4
6
8
(1)汽车所行路程与耗油量有什么关系?
(2)汽车行驶,耗油多少升?
(3)当油箱还剩油时,汽车还能行驶多少千米?
16.同一时间、同一地点测得树高和影长的数据如表:
树高
2
3
4
6
影长
1.6
2.4
3.2
4.8
(1)在图中描出表示树高和对应影长的点,然后把它们连起来.
(2)连线以后观察,它们是在一条直线上吗?
,说明树高和影长成
关系.
(3)不计算,利用图象判断,树高8米时,影长
米?影长4米时,树高
米?
17.食堂每天开饭人数与购买蔬菜的数量如表:
每天开饭人数个
0
1
2
3
4
5
6
7
8
购买蔬菜的数量千克
0
0.5
1
1.5
2
(1)根据已知的数量关系补充完整上面的表格.
(2)根据表中的数在下面图中描出对应的点,再把各个点连接起来.
(3)上面的两种量成比例吗?如果成,成什么比例,为什么?
答案
一、选择题
1.2..3..4..5..6..7..
二、填空题
1.速度,时间,速度,时间,反.
2.:,.
3.;.
4.:反,正.
5.18、7、9、27、10.
6..
三、判断题
1..2..3..4..5..6..7.
四、解答题
1.解:①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
时间时
1
2
3
4
5
6
路程千米
90
180
270
360
450
540
②时间和路程成
正比例,理由是
路程时间速度(一定).
③如图
用图象估计一下,2.5时行
225千米,行675千米需要
7.5小时.
故答案为:正,路程时间速度(一定),225,7.5.
2.解:(1)表中有汽车数量和运货质量两种量,它们是两种相关联的量,一个量变大,另一个量也随着变大,它们的比值一定,所以汽车数量和运货质量成正比例关系.
(2),,,,它们的比值相等.
(3)根据题意可知,这个比值表示每辆汽车的运货质量.
(4)相关联的两种量成正比例,因为它们的比值一定.
故答案为:汽车数量;运货质量;运货质量;汽车数量.
3.解:(1)甲:(一定),是比值一定,所以甲车的运货量与运货次数成正比例关系.
乙:(一定),是比值一定,所以乙车的运货量与运货次数成正比例关系.
(2)
(吨
(吨
答:甲、乙两车各运货6次,运货量相差12吨.
4.解:从甲港开到乙港的速度:(千米时).
从乙港开到丙港的速度:(千米时).
答:轮船从甲港开到乙港,从乙港开到丙港的速度都是25千米时.
(2)由(1)可知(一定),是比值一定,所以轮船行驶的路程和所用时间成正比例.
(3)设表示路程,表示时间,表示速度,则等量关系为:.
5.解:
数量份
0
2
4
6
8
10
总价元
0
36
72
108
144
180
(1)总价与质量成正比例.
(2)根据表格中数据可在右图中描点连线,得出统计图如图:
(3)点在这条直线上,这一点表示15份套餐需要270元钱.
(4)(元),
(份),
答:买3份该套餐要付54元钱,126元可以买7份该套餐.
6.解:(1)答:高速动车4分钟行驶16千米.
(2)(千米时);
答:高速动车的速度是240千米时.
(3)因为速度(一定),所以高速动车所行驶的路程和时间成正比例.
(4)(小时);
答:高速动车需要1.625小时.
(5)(千米);
故答案为:16;4;正;1.625.
7.解:如图:
8.解:(1)表中相关联的量是时间(天)和生产量(吨).
(2)根据表中的数据,写出一个比例:(答案不唯一).
(3)表中相关联的两种量成正比例关系.
(4)在图中描出表示时间和相应生产量的点,并把它们按顺序连接起来(下图).
(5)估计生产550吨纸片,大约需要8天(填整数)(下图红色虚线与横轴的交点).
故答案为:时间(天),生产量(吨),(答案不唯一),正比例,8.
9.解:
10.解:(1)
时间分
5
10
15
20
25
30
路程千米
4
8
12
16
20
24
(2)不计算,根据图象估计一下,长颈鹿跑,大约要12.5分钟.
(3)长颈鹿奔跑的路程和时间是成比例;成正比例.
故答案为:12.5,正,
11.解:(1)(一定),
因为每米高影长的物体(一定),所以杆高和它的影长成正比例;
(2)绘制统计图如下图,观察发现:表示树高和对应影长的点,都在一条直线上;
12.解:(1)如果塑料袋挂在竹竿左右两边刻度相同的地方,左边放5个棋子,右边应放5个棋子才能保持保证竹竿平衡.
(2)设左边应放个棋子才能保证平衡,
答:应该放6个棋子才能保证平衡.
同理:
;
;
;
.
为了保证平衡,左边还可以怎么放?找出规律,填写下表.
左边刻度
1
2
3
6
所放棋子数
30
15
10
5
乘积
(3)因为动力动力臂阻力阻力臂,也就是积一定,所以发现刻度数与所放棋子数成反比例关系.
故答案为:5;6;
13.解:(1)用煤的吨数用煤的天数每天的用煤量(一定)
根据两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就是成正比例的量
因此可判断用煤天数和用煤量成正比例关系.
(2)如果用表示用煤的数,表示用煤的天数,表示每天的用煤量,它们之间的关系可以表示为(一定).
(3)根据图象可判断:5天有煤1.5吨;2.4吨煤可以用8天.
故答案为:(一定).
14.解:(1)(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
填表如下:
1
2
3
4
6
8
12
24
48
96
48
32
24
16
12
8
4
2
(1)随着的增加而减少.
(2)因为底高平行四边形的面积(一定),所以平行四边形底和高成反比例.
(3)设高为厘米,
.
答:高是6.4厘米.
15.解:(1)耗油量随着路程的变化而变化,因为、即每升油所行路程不变,所以汽车所行路程和耗油量成正比例关系;
(2)因为耗油量路程每升油所行路程,
升)
答:要耗油12升.
(3)因为路程每升油所行路程耗油量,
(千米)
答:汽车大约还能行驶22.5千米.
16.解:(1)所作图象如下图,观察发现:表示树高和对应影长的点,都在一条直线上.
(2)连线以后,发现表示树高和对应影长的点,都在一条直线上,这说明树高和影长成正比例关系,
因为随着树的高度的增加,影长也在增加,且树高与影长的商是一定的,所以树高和影长成正比例关系;
(3)设树高8时,影长为米,影长时,树高米,
则有
;
答:树高时,影长6.4米,影长时,树高5米.
故答案为:在、正比例;
6.4,5.
17.解:(1)食堂每天开饭人数与购买蔬菜的数量如下表:
每天开饭人数个
0
1
2
3
4
5
6
7
8
购买蔬菜的数量千克
0
0.5
1
1.5
2
2.5
3
3.5
4
(2)作图如下:
(3)因为(一定),所以购买蔬菜的数量和人数成正比例关系.
答:成比例;因为(一定),所以购买蔬菜的数量和人数成正比例关系.
