苏科版七年级下册数学课件 11.2不等式的解集(15张)
文档属性
| 名称 | 苏科版七年级下册数学课件 11.2不等式的解集(15张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-28 00:00:00 | ||
图片预览






文档简介
为了保障交通安全、畅通,隧道入口处常有汽车限高标识.若某隧道的限高为4.2m,那么高度为3m、3.5m、4m、4.5m的汽车允许通过这个隧道吗?
新课探索
设汽车的高度为xm,
则x≤4.2
当x=3、 x=3.5、 x=4时,这个不等式成立.
像这样,能使不等式成立的未知数的值叫做不等式的解。
试一试
分别说出使下列不等式成立的x的值
(1)x-3>0
(2)x-4≤0
1、不等式x-3>0的解有几个?
【想一想】
2、不等式x-3>0的解与方程x-3=0的解有什么不同?
方程的解只有一个
而不等式的解有无数个,而且这无数个解有一个共同特征.
例如:不等式x-3>0的所有解,都是大于3的数,所以我们就可以说x>3是不等式x-3>0的解集.
方程x-3=0的解呢?
一个含有未知数的不等式的所有的解,组成这个不等式的解的集合,简称这个不等式的解集.
*不等式的解集:
练一练:
说出下列不等式的解集
(1)x-2<0
(2)x+4≤0
求不等式解集的过程叫做___________.
解不等式
【想一想】
你能在数轴上表示出一个不等式的解集x>3吗?
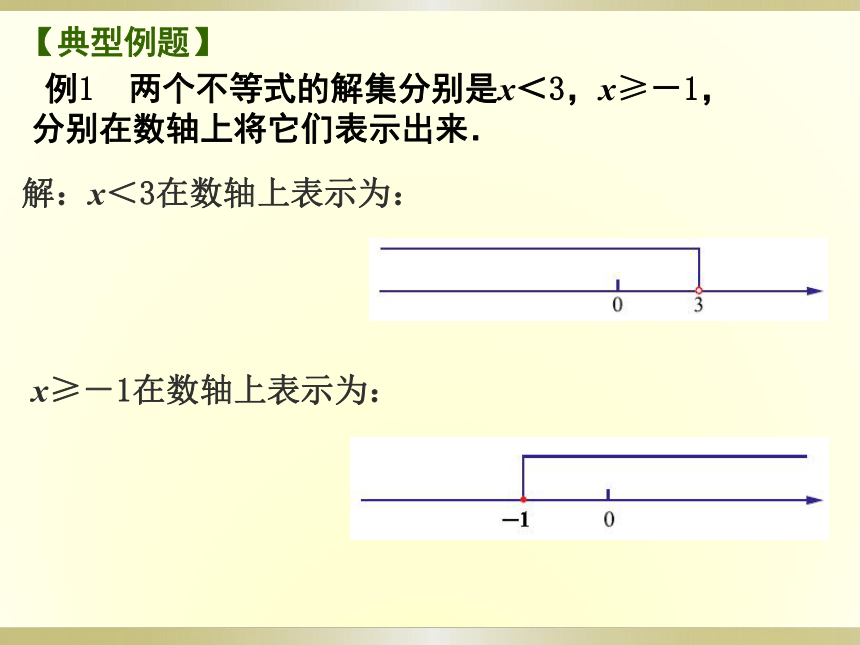
例1 两个不等式的解集分别是x<3,x≥-1,分别在数轴上将它们表示出来.
【典型例题】
解:x<3在数轴上表示为:
x≥-1在数轴上表示为:
【理一理】
(1)先确定区分的这个界点
(2)确定方向,在界点的左边还是右边
<,≤都向左边画
>,≥都向右边画
(3)不包括这个数画“小空心圆圈”
包括这个数画“小实心点”
【典型例题】
例2 写出图中所表示的不等式的解集:
解:(1)图中所表示的不等式的解集为x<5;
(2)图中所表示的不等式的解集为x≥-6.
(1)
(2)
例3 不等式x≤2的正整数解是( )
A.1; B.0,1;
C.1,2; D.0,1,2.
C
【典型例题】
所以某些限制的条件下,不等式的解的个数也可以是有限个数
-3,-2,-1,0,1,2
概念辨析
根据“当x为任何正数时,都能使不等式
x+2>1成立”,能不能说“不等式x+2>1的解集为x>0”? 为什么?
不可以,因为x>0并没有把所有的解都包括进去,只是其中的一部分,所以不能称为不等式的解集。
下列说法中正确的是:
1. 4是x+3>6的解
2. x+3<6的解集是x<2
3. 3是x+3≤6的解
4. x>4是不等式x+3≥6的解集的一部分.
(√)
(×)
(√)
(√)
1.写出下列各图所表示的不等式的解集
x≥-0.5
-2≤x<2
x<0
【练一练】
2. 在数轴上表示下列不等式的解集:
(1)x>-1; (2)-2<X≤3; (3)-2≤x<3.
3.用不等式表示下列数量关系,再用数轴表示出来:
(1)x小于-1; (2)x不小于-1;
(3)a是正数; (4)所有不大于4的正数.
【练一练】
3.分别写出一个不等式,使它的解集满足下列条件.
(1)x=-1是不等式的一个解,
提高练习
(2)它的正整数解为1、2、3、4.
收获和体会
不等式的解
不等式的解集
解不等式
不等式解集的表示方法
新课探索
设汽车的高度为xm,
则x≤4.2
当x=3、 x=3.5、 x=4时,这个不等式成立.
像这样,能使不等式成立的未知数的值叫做不等式的解。
试一试
分别说出使下列不等式成立的x的值
(1)x-3>0
(2)x-4≤0
1、不等式x-3>0的解有几个?
【想一想】
2、不等式x-3>0的解与方程x-3=0的解有什么不同?
方程的解只有一个
而不等式的解有无数个,而且这无数个解有一个共同特征.
例如:不等式x-3>0的所有解,都是大于3的数,所以我们就可以说x>3是不等式x-3>0的解集.
方程x-3=0的解呢?
一个含有未知数的不等式的所有的解,组成这个不等式的解的集合,简称这个不等式的解集.
*不等式的解集:
练一练:
说出下列不等式的解集
(1)x-2<0
(2)x+4≤0
求不等式解集的过程叫做___________.
解不等式
【想一想】
你能在数轴上表示出一个不等式的解集x>3吗?
例1 两个不等式的解集分别是x<3,x≥-1,分别在数轴上将它们表示出来.
【典型例题】
解:x<3在数轴上表示为:
x≥-1在数轴上表示为:
【理一理】
(1)先确定区分的这个界点
(2)确定方向,在界点的左边还是右边
<,≤都向左边画
>,≥都向右边画
(3)不包括这个数画“小空心圆圈”
包括这个数画“小实心点”
【典型例题】
例2 写出图中所表示的不等式的解集:
解:(1)图中所表示的不等式的解集为x<5;
(2)图中所表示的不等式的解集为x≥-6.
(1)
(2)
例3 不等式x≤2的正整数解是( )
A.1; B.0,1;
C.1,2; D.0,1,2.
C
【典型例题】
所以某些限制的条件下,不等式的解的个数也可以是有限个数
-3,-2,-1,0,1,2
概念辨析
根据“当x为任何正数时,都能使不等式
x+2>1成立”,能不能说“不等式x+2>1的解集为x>0”? 为什么?
不可以,因为x>0并没有把所有的解都包括进去,只是其中的一部分,所以不能称为不等式的解集。
下列说法中正确的是:
1. 4是x+3>6的解
2. x+3<6的解集是x<2
3. 3是x+3≤6的解
4. x>4是不等式x+3≥6的解集的一部分.
(√)
(×)
(√)
(√)
1.写出下列各图所表示的不等式的解集
x≥-0.5
-2≤x<2
x<0
【练一练】
2. 在数轴上表示下列不等式的解集:
(1)x>-1; (2)-2<X≤3; (3)-2≤x<3.
3.用不等式表示下列数量关系,再用数轴表示出来:
(1)x小于-1; (2)x不小于-1;
(3)a是正数; (4)所有不大于4的正数.
【练一练】
3.分别写出一个不等式,使它的解集满足下列条件.
(1)x=-1是不等式的一个解,
提高练习
(2)它的正整数解为1、2、3、4.
收获和体会
不等式的解
不等式的解集
解不等式
不等式解集的表示方法
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
