苏科版八年级下册数学 9.5三角形的中位线 课件(共15张)
文档属性
| 名称 | 苏科版八年级下册数学 9.5三角形的中位线 课件(共15张) |  | |
| 格式 | ppt | ||
| 文件大小 | 571.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-19 18:00:43 | ||
图片预览



文档简介
9.5 三角形的中位线
教学目标:
1、理解三角形中位线的定义;
2、探索并证明三角形中位线的性质定理;
3、学会用三角形中位线解决问题。
情景创设
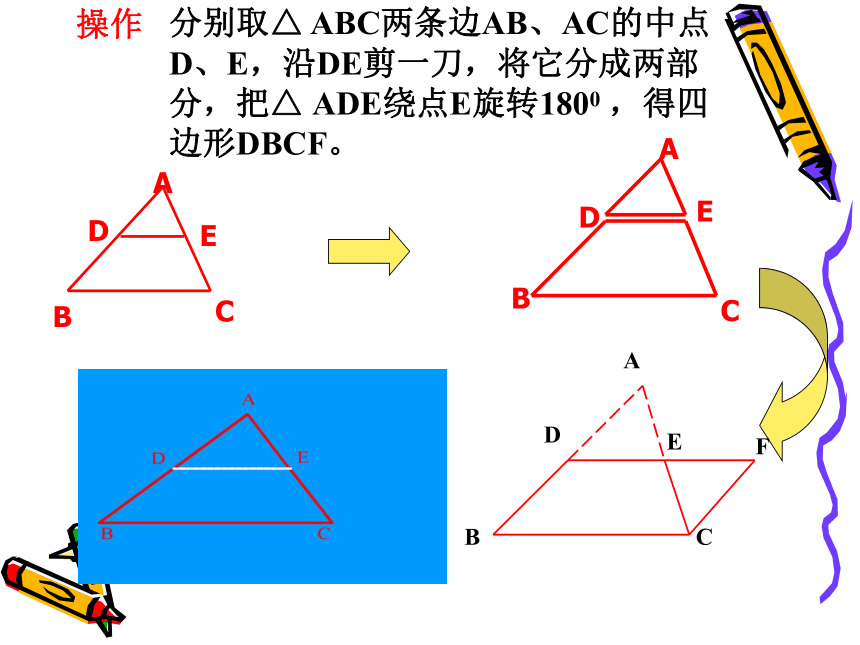
怎样将一张三角形纸片剪成两部分,将分成的两部分拼成一个平行四边形?
分别取△ ABC两条边AB、AC的中点D、E,沿DE剪一刀,将它分成两部分,把△ ADE绕点E旋转1800 ,得四边形DBCF。
操作
A
B
C
D
E
A
D
E
B
C
D
E
A
B
C
F
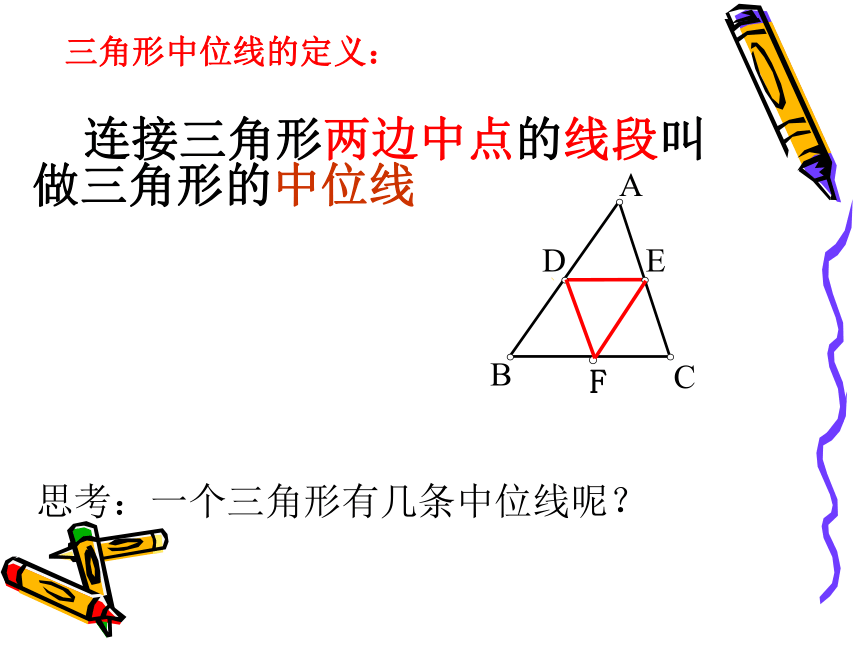
三角形中位线的定义:
连接三角形两边中点的线段叫做三角形的中位线
F
思考:一个三角形有几条中位线呢?
C
E
D
B
A
A
B
C
D
E
A
D
E
B
C
D
E
A
B
C
F
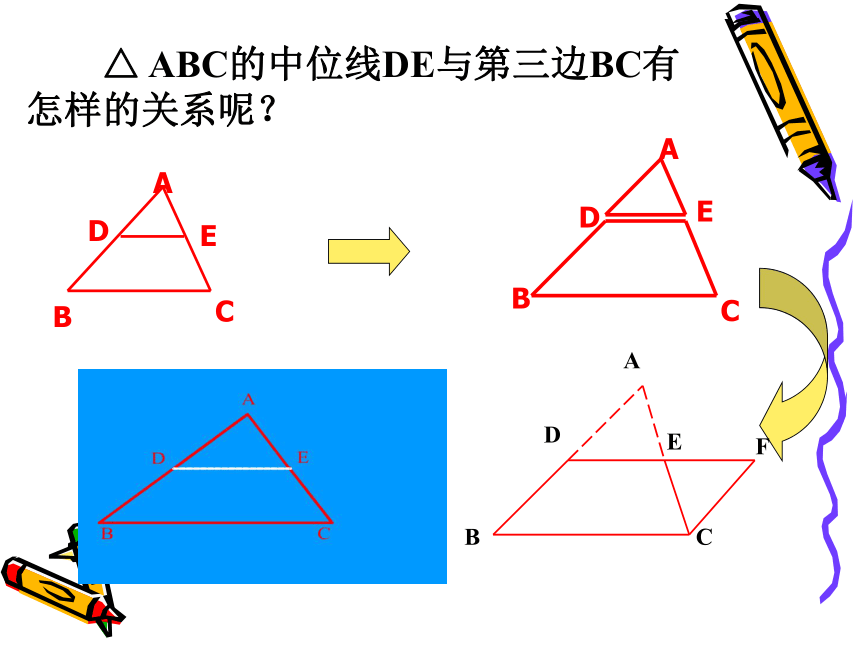
△ ABC的中位线DE与第三边BC有怎样的关系呢?
C
E
D
F
B
A
.
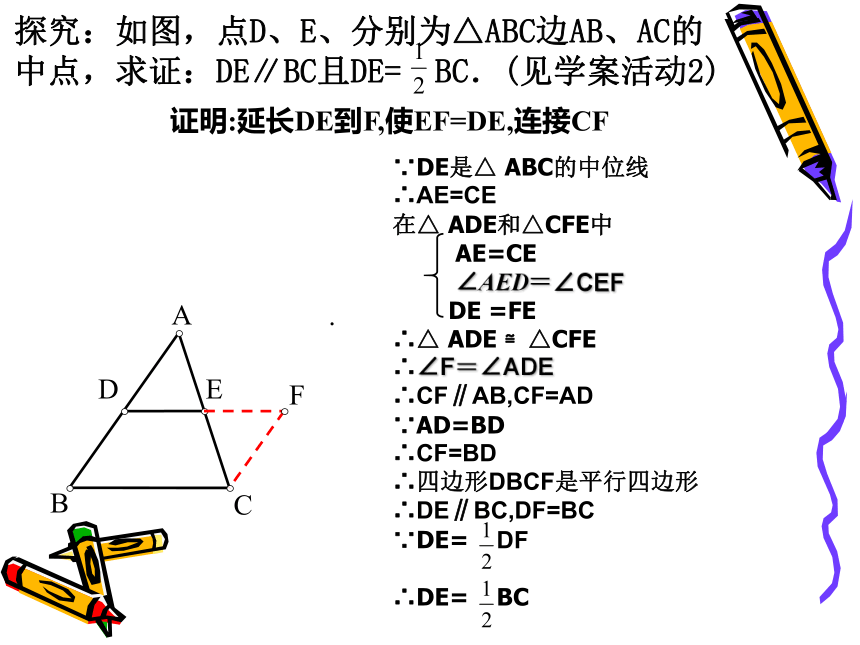
证明:延长DE到F,使EF=DE,连接CF
探究:如图,点D、E、分别为△ABC边AB、AC的中点,求证:DE∥BC且DE= BC.(见学案活动2)
∵DE是△ ABC的中位线
∴AE=CE
在△ ADE和△CFE中
AE=CE
∠AED=∠CEF
DE =FE
∴△ ADE ≌△CFE
∴∠F=∠ADE
∴CF∥AB,CF=AD
∵AD=BD
∴CF=BD
∴四边形DBCF是平行四边形
∴DE∥BC,DF=BC
∵DE= DF
∴DE= BC
三角形中位线的性质定理:
三角形的中位线平行于第三边,并且等于它的一半。
用符号语言表示
∴ __
∥
____,
DE=
___
BC.
DE
BC
2
1
∵DE是△ ABC的中位线
C
E
D
B
A
C
B
A
E
D
F
1.如图,D﹑E﹑F分别是△ABC三边中点(学案练习1)
(1).图中有 个平行四边形
(2)图中有哪些全等的三角形?
(3).中点三角形DEF与△ABC面积有何关系?周长有何关系
△ABC中,D、E、F分别是AB、 AC、BC的中点,试说明 AF与DE互相平分
C
A
B
D
E
F
连中位线.
2.
例题讲解
在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,四边形EFGH是平行四边形吗?为什么?(见学案)
A
B
C
D
E
F
G
H
例题
讲解
变式一:
如果上述条件不变,若AC=BD,
那么四边形EFGH是什么四边形?
为什么?
A
E
B
F
C
G
D
H
例题
讲解
变式二
如果上述条件不变,若AC BD,猜想
四边形EFGH的形状,并说明理由。
A
B
C
D
E
F
G
H
O
M
N
H
例题
讲解
A
B
C
D
E
F
G
H
变式三
如果上述条件不变,若AC BD,AC=BD,
猜想四边形EFGH的形状,并说明理由。
课堂小结
1.理解三角形中位线的定义:
连接三角形两边中点的线段叫做三角形的中位线。
2.掌握三角形中位线的性质:
三角形的中位线平行与第三边,并且等于它的一半。
3.能应用三角形中位线的性质解决有关计算或说理等问题。
教学目标:
1、理解三角形中位线的定义;
2、探索并证明三角形中位线的性质定理;
3、学会用三角形中位线解决问题。
情景创设
怎样将一张三角形纸片剪成两部分,将分成的两部分拼成一个平行四边形?
分别取△ ABC两条边AB、AC的中点D、E,沿DE剪一刀,将它分成两部分,把△ ADE绕点E旋转1800 ,得四边形DBCF。
操作
A
B
C
D
E
A
D
E
B
C
D
E
A
B
C
F
三角形中位线的定义:
连接三角形两边中点的线段叫做三角形的中位线
F
思考:一个三角形有几条中位线呢?
C
E
D
B
A
A
B
C
D
E
A
D
E
B
C
D
E
A
B
C
F
△ ABC的中位线DE与第三边BC有怎样的关系呢?
C
E
D
F
B
A
.
证明:延长DE到F,使EF=DE,连接CF
探究:如图,点D、E、分别为△ABC边AB、AC的中点,求证:DE∥BC且DE= BC.(见学案活动2)
∵DE是△ ABC的中位线
∴AE=CE
在△ ADE和△CFE中
AE=CE
∠AED=∠CEF
DE =FE
∴△ ADE ≌△CFE
∴∠F=∠ADE
∴CF∥AB,CF=AD
∵AD=BD
∴CF=BD
∴四边形DBCF是平行四边形
∴DE∥BC,DF=BC
∵DE= DF
∴DE= BC
三角形中位线的性质定理:
三角形的中位线平行于第三边,并且等于它的一半。
用符号语言表示
∴ __
∥
____,
DE=
___
BC.
DE
BC
2
1
∵DE是△ ABC的中位线
C
E
D
B
A
C
B
A
E
D
F
1.如图,D﹑E﹑F分别是△ABC三边中点(学案练习1)
(1).图中有 个平行四边形
(2)图中有哪些全等的三角形?
(3).中点三角形DEF与△ABC面积有何关系?周长有何关系
△ABC中,D、E、F分别是AB、 AC、BC的中点,试说明 AF与DE互相平分
C
A
B
D
E
F
连中位线.
2.
例题讲解
在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,四边形EFGH是平行四边形吗?为什么?(见学案)
A
B
C
D
E
F
G
H
例题
讲解
变式一:
如果上述条件不变,若AC=BD,
那么四边形EFGH是什么四边形?
为什么?
A
E
B
F
C
G
D
H
例题
讲解
变式二
如果上述条件不变,若AC BD,猜想
四边形EFGH的形状,并说明理由。
A
B
C
D
E
F
G
H
O
M
N
H
例题
讲解
A
B
C
D
E
F
G
H
变式三
如果上述条件不变,若AC BD,AC=BD,
猜想四边形EFGH的形状,并说明理由。
课堂小结
1.理解三角形中位线的定义:
连接三角形两边中点的线段叫做三角形的中位线。
2.掌握三角形中位线的性质:
三角形的中位线平行与第三边,并且等于它的一半。
3.能应用三角形中位线的性质解决有关计算或说理等问题。
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
