9.2多边形的内角与外角和 同步课时训练(含答案)
文档属性
| 名称 | 9.2多边形的内角与外角和 同步课时训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 351.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-18 00:00:00 | ||
图片预览


文档简介
9.2多边形的内角与外角和课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
A.10 B.11 C.12 D.13
2.一个多边形的内角和等于它的外角和的false倍,则它是( )边形.
A.六 B.七 C.八 D.九
3.如果一个多边形的内角和为false,那么从这个多边形的一个顶点可以作( )条对角线.
A.false B.false C.false D.false
4.从五边形的一个顶点出发,可以画出false条对角线,它们将五边形分成false个三角形.则false、false的值分别为( )
A.1,2 B.2,3 C.3,4 D.4,4
5.一个多边形的每个外角都等于相邻内角的false,这个多边形为( )
A.六边形 B.八边形 C.十边形 D.十二边形
6.科技馆为某机器人编制了一个程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为( )
A.12米 B.16米 C.18米 D.20米
7.如图,四边形ABCD是轴对称图形,直线AC是对称轴.如果∠BAD+∠BCD=210°,那么∠B+∠D等于( )
A.150° B.105° C.100° D.70°
8.如图,有一个正五边形木框,若要保证它不变形,需要再钉的木条根数至少是( )
A.1 B.2 C.3 D.4
9.一个多边形的外角和是360°,这个多边形是( )
A.四边形 B.五边形 C.六边形 D.不确定
10.若过六边形的一个顶点可以画false条对角线,则false的值是( )
A.1 B.2 C.3 D.4
二、填空题
11.若从一个n边形的一个顶点出发,最多可以引7条对角线,则n=_____.
12.一个正多边形的内角和为false,则这个多边形的外角的度数为______.
13.如图所示,小梦发现将正六边形false的边向两端延长后,可以构成 “六边星角形”,则图中false的度数是_________.
14.若一个多边形的内角和是false,则该多边形的边数是_____.
15.如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°…照这样走下去,他第一次回到出发点A时,共走路程为____米.
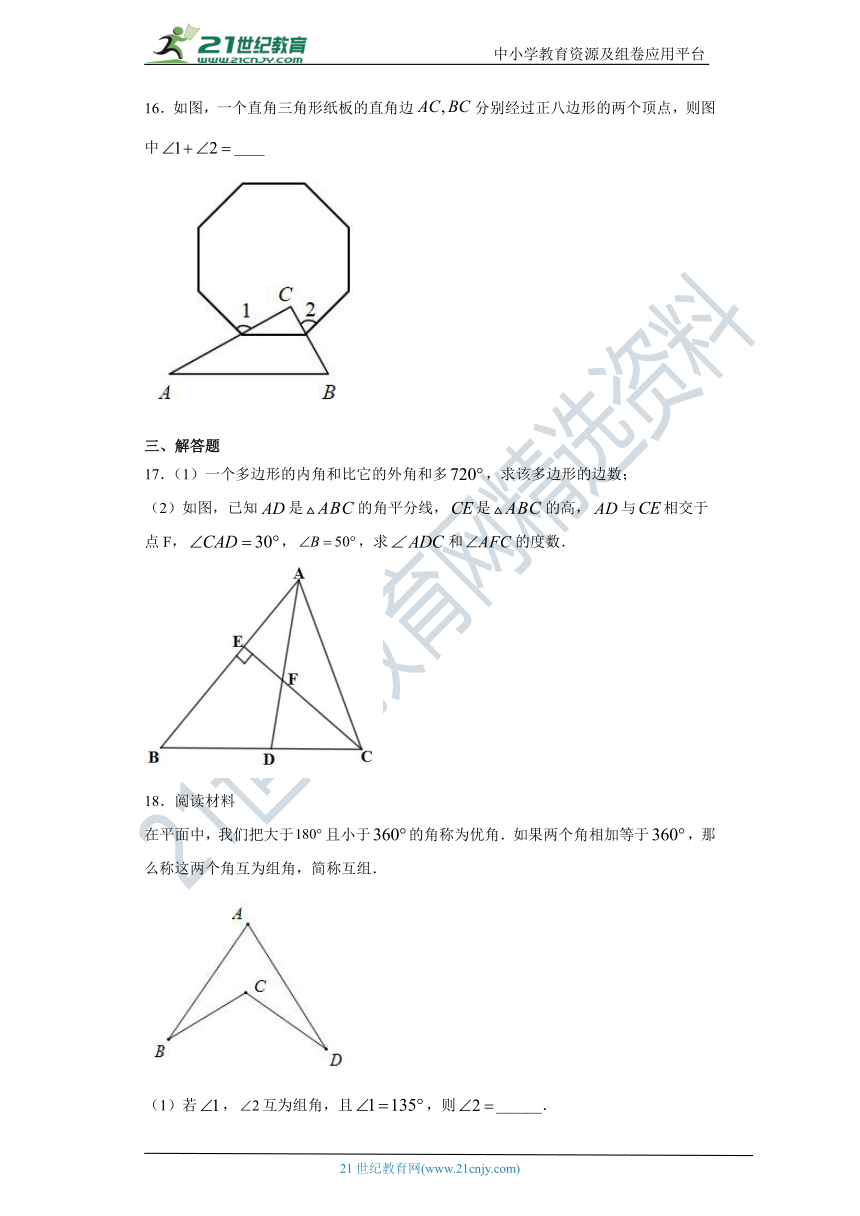
16.如图,一个直角三角形纸板的直角边false分别经过正八边形的两个顶点,则图中false____
三、解答题
17.(1)一个多边形的内角和比它的外角和多false,求该多边形的边数;
(2)如图,已知false是false的角平分线,false是false的高,false与false相交于点F,false,false,求false和false的度数.
18.阅读材料
在平面中,我们把大于false且小于false的角称为优角.如果两个角相加等于false,那么称这两个角互为组角,简称互组.
(1)若false,false互为组角,且false,则false______.
习惯上,我们把有一个内角大于false的四边形俗称为镖形.
(2)如图,在镖形ABCD中,优角false与钝角false互为组角,试探索内角false,false,false与钝角false之间的数量关系,并至少用两种以上的方法说明理由.
19.在一个各内角都相等的多边形中,每一个内角都比相邻外角的false倍还大false.
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
20.如图,false,false,false,false是五边形ABCDE的外角,且false,false,求∠AED.
参考答案
1.C
2.C
3.C
4.B
5.B
6.C
7.A
8.B
9.D
10.C
11.10
12.60°
13.60°
14.5
15.64
16.180?
17.(1)该多边形的边数为8;(2)false;false.
【详解】
解:(1)设该多边形的边数为n,由已知,得
false,
解得false,
∴该多边形的边数为8;
(2)∵false是false的角平分线,且false,
∴false,false,
又∵false,
∴false,
∵false是false的高,
∴false,
∴false.
18.(1)225°;(2)钝角∠BCD=∠A+∠B+∠D,理由见解析.
【详解】
解:(1)∵∠1、∠2互为组角,且∠1=135°,
∴∠2=360°-∠1=225°,
故答案为:225°;
(2)钝角∠BCD=∠A+∠B+∠D.
理由如下:
理由①:∵在四边形ABCD中,∠A+∠B+优角∠BCD+∠D=360°,
又∵优角∠BCD+钝角∠BCD=360°?,
∴钝角∠BCD=∠A+∠B+∠D;
理由②:如下图,连接AC并延长,
∵∠BAC+∠B=∠BCE,∠DAC+∠D=∠DCE(三角形外角的性质),
∴钝角∠BCD=∠BCE+∠DCE=∠BAC+∠B+∠DAC+∠D=∠A+∠B+∠D.
19.(1)9;(2)1080?或1260?或1440?.
【详解】
解:(1)设每一个外角为false,则与其相邻的内角等于false,
false,
false,即多边形的每个外角为false,
∵多边形的外角和为false,
∴多边形的外角个数为:false,
∴这个多边形的边数为false;
(2)因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,
①若剪去一角后边数减少1条,即变成false边形,
false内角和为false,
②若剪去一角后边数不变,即变成false边形,
false内角和为false,
③若剪去一角后边数增加1,即变成false边形,
false内角和为false,
∴将这个多边形剪去一个角后,剩下多边形的内角和为false或false或 false.
20.false
【详解】
解:∵五边形false
∴∠BAE+∠ABC+∠BCD+∠CDE+∠AED=540°
又∵false是五边形false的外角,且false,
∴false,
false
∴false.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
A.10 B.11 C.12 D.13
2.一个多边形的内角和等于它的外角和的false倍,则它是( )边形.
A.六 B.七 C.八 D.九
3.如果一个多边形的内角和为false,那么从这个多边形的一个顶点可以作( )条对角线.
A.false B.false C.false D.false
4.从五边形的一个顶点出发,可以画出false条对角线,它们将五边形分成false个三角形.则false、false的值分别为( )
A.1,2 B.2,3 C.3,4 D.4,4
5.一个多边形的每个外角都等于相邻内角的false,这个多边形为( )
A.六边形 B.八边形 C.十边形 D.十二边形
6.科技馆为某机器人编制了一个程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为( )
A.12米 B.16米 C.18米 D.20米
7.如图,四边形ABCD是轴对称图形,直线AC是对称轴.如果∠BAD+∠BCD=210°,那么∠B+∠D等于( )
A.150° B.105° C.100° D.70°
8.如图,有一个正五边形木框,若要保证它不变形,需要再钉的木条根数至少是( )
A.1 B.2 C.3 D.4
9.一个多边形的外角和是360°,这个多边形是( )
A.四边形 B.五边形 C.六边形 D.不确定
10.若过六边形的一个顶点可以画false条对角线,则false的值是( )
A.1 B.2 C.3 D.4
二、填空题
11.若从一个n边形的一个顶点出发,最多可以引7条对角线,则n=_____.
12.一个正多边形的内角和为false,则这个多边形的外角的度数为______.
13.如图所示,小梦发现将正六边形false的边向两端延长后,可以构成 “六边星角形”,则图中false的度数是_________.
14.若一个多边形的内角和是false,则该多边形的边数是_____.
15.如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°…照这样走下去,他第一次回到出发点A时,共走路程为____米.
16.如图,一个直角三角形纸板的直角边false分别经过正八边形的两个顶点,则图中false____
三、解答题
17.(1)一个多边形的内角和比它的外角和多false,求该多边形的边数;
(2)如图,已知false是false的角平分线,false是false的高,false与false相交于点F,false,false,求false和false的度数.
18.阅读材料
在平面中,我们把大于false且小于false的角称为优角.如果两个角相加等于false,那么称这两个角互为组角,简称互组.
(1)若false,false互为组角,且false,则false______.
习惯上,我们把有一个内角大于false的四边形俗称为镖形.
(2)如图,在镖形ABCD中,优角false与钝角false互为组角,试探索内角false,false,false与钝角false之间的数量关系,并至少用两种以上的方法说明理由.
19.在一个各内角都相等的多边形中,每一个内角都比相邻外角的false倍还大false.
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
20.如图,false,false,false,false是五边形ABCDE的外角,且false,false,求∠AED.
参考答案
1.C
2.C
3.C
4.B
5.B
6.C
7.A
8.B
9.D
10.C
11.10
12.60°
13.60°
14.5
15.64
16.180?
17.(1)该多边形的边数为8;(2)false;false.
【详解】
解:(1)设该多边形的边数为n,由已知,得
false,
解得false,
∴该多边形的边数为8;
(2)∵false是false的角平分线,且false,
∴false,false,
又∵false,
∴false,
∵false是false的高,
∴false,
∴false.
18.(1)225°;(2)钝角∠BCD=∠A+∠B+∠D,理由见解析.
【详解】
解:(1)∵∠1、∠2互为组角,且∠1=135°,
∴∠2=360°-∠1=225°,
故答案为:225°;
(2)钝角∠BCD=∠A+∠B+∠D.
理由如下:
理由①:∵在四边形ABCD中,∠A+∠B+优角∠BCD+∠D=360°,
又∵优角∠BCD+钝角∠BCD=360°?,
∴钝角∠BCD=∠A+∠B+∠D;
理由②:如下图,连接AC并延长,
∵∠BAC+∠B=∠BCE,∠DAC+∠D=∠DCE(三角形外角的性质),
∴钝角∠BCD=∠BCE+∠DCE=∠BAC+∠B+∠DAC+∠D=∠A+∠B+∠D.
19.(1)9;(2)1080?或1260?或1440?.
【详解】
解:(1)设每一个外角为false,则与其相邻的内角等于false,
false,
false,即多边形的每个外角为false,
∵多边形的外角和为false,
∴多边形的外角个数为:false,
∴这个多边形的边数为false;
(2)因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,
①若剪去一角后边数减少1条,即变成false边形,
false内角和为false,
②若剪去一角后边数不变,即变成false边形,
false内角和为false,
③若剪去一角后边数增加1,即变成false边形,
false内角和为false,
∴将这个多边形剪去一个角后,剩下多边形的内角和为false或false或 false.
20.false
【详解】
解:∵五边形false
∴∠BAE+∠ABC+∠BCD+∠CDE+∠AED=540°
又∵false是五边形false的外角,且false,
∴false,
false
∴false.
