10.5图形的全等 同步课时训练(含答案)
文档属性
| 名称 | 10.5图形的全等 同步课时训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 289.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-18 00:00:00 | ||
图片预览


文档简介
10.5图形的全等课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法正确的是( )
A.两个长方形是全等图形 B.形状相同的两个三角形全等
C.两个全等图形面积一定相等 D.所有的等边三角形都是全等三角形
2.下列说法中,正确的有( )
①正方形都是全等形;②等边三角形都是全等形;③形状相同的图形是全等形;④大小相同的图形是全等形;⑤能够完全重合的图形是全等形.
A.1个 B.2个 C.3个 D.4个
3.如图,在false中,false分别是false上的点,若false,则false的度数是( )
A.false B.false C.false D.false
4.下列四个图形中,全等的图形是( )
A.①和②???????????????? B.①和③ C.②和③ D.③和④
5.下列各组中的两个图形为全等形的是( ).
A.两块三角尺 B.两枚硬币 C.两张 A4 纸 D.两片枫树叶
6.如图,已知△ABC≌△CDE,下列结论中不正确的是( )
A.AC=CE B.∠BAC=∠ECD C.∠ACB=∠ECD D.∠B=∠D
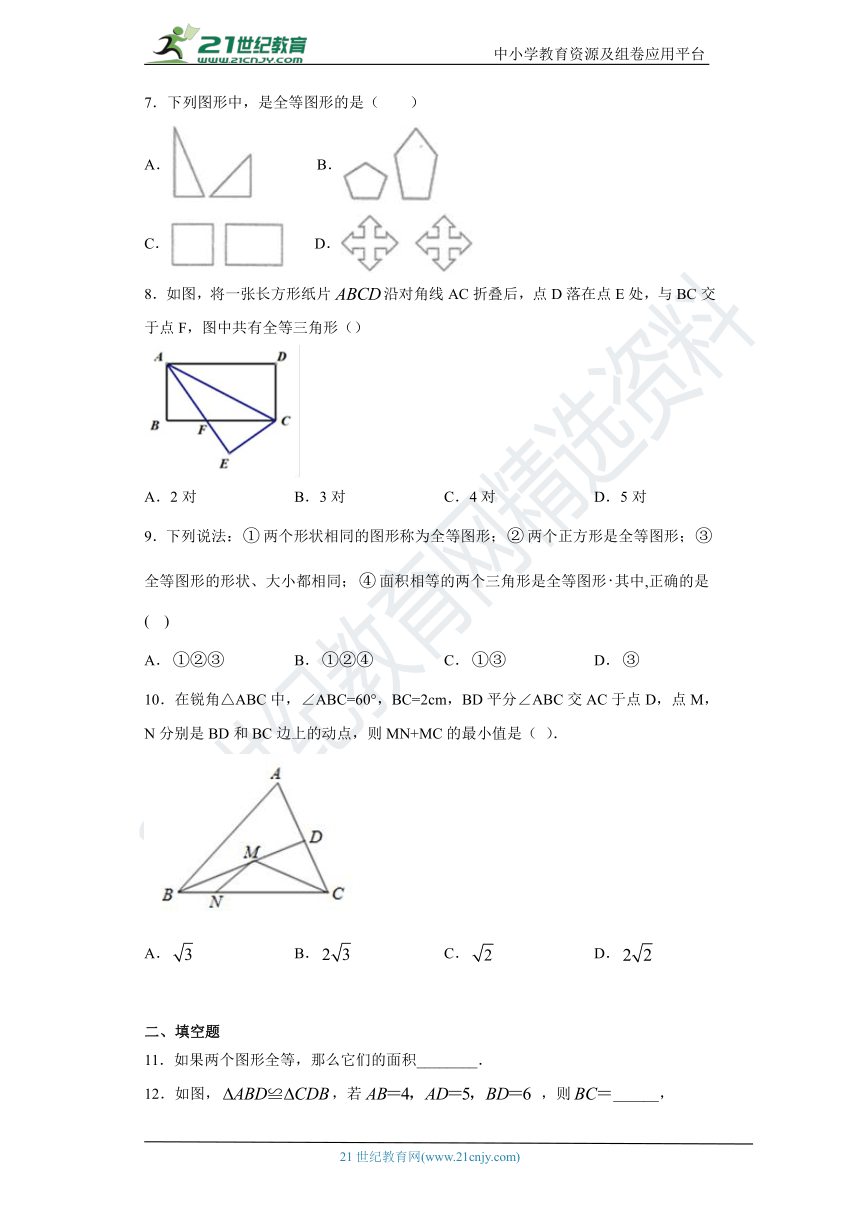
7.下列图形中,是全等图形的是( )
A. B.
C. D.
8.如图,将一张长方形纸片false沿对角线AC折叠后,点D落在点E处,与BC交于点F,图中共有全等三角形()
A.2对 B.3对 C.4对 D.5对
9.下列说法:false两个形状相同的图形称为全等图形;false两个正方形是全等图形;false全等图形的形状、大小都相同;false面积相等的两个三角形是全等图形false其中,正确的是(????)
A.false B.false C.false D.false
10.在锐角△ABC中,∠ABC=60°,BC=2cm,BD平分∠ABC交AC于点D,点M,N分别是BD和BC边上的动点,则MN+MC的最小值是( ).
A.false B.false C.false D.false
二、填空题
11.如果两个图形全等,那么它们的面积________.
12.如图,false,若false ,则false______,false______.
13.若两个三角形全等,那么它们对应的高、中线、角平分线的关系是相等.(____)
14.如图,四边形EFGH与四边形ABCD是全等图形,若AD=5,∠B=70°.则 EH=________?,∠F=________?.
15.如图, 已知△ABC≌△ADC,∠BAC=60°,∠ACD=24°, 那么∠D=________°.
16.如图,△ABD≌△ACE,且∠BAD和∠CAE,∠ABD和∠ACE,∠ADB和∠AEC是对应角,则对应边_________.
三、解答题
17.如图,点false是正方形false内的一点,将false绕点false顺时针旋转90°至false,指出图中的全等图形以及它们的对应顶点、对应边和对应角.若已知false,false,求false的度数.
18.如图,在等腰△ABC中,AB=BC,点D是AC边的中点,延长BD至点E,使得DE=BD,连结CE.
(1)求证:△ABD≌△CED.
(2)当BC=5,CD=3时,求△BCE的周长.
19.如图,点E,H,G,N在同一直线上,△EFG≌△NMH,∠F和∠M是对应角.在△EFG中,FG是最长边.在△NMH中,MH是最长边.已知EF=2.1 cm,EH=1.1 cm,HN=3.3 cm.
(1)写出其他对应边及对应角;
(2)求线段MN及线段HG的长度.
20.如图,在等腰△ABC中,CB=CA,延长AB至点D,使DB=CB,连接CD,以CD为边作等腰△CDE,使CE=CD,∠ECD=∠BCA,连接BE交CD于点M.
(1)BE=AD吗?请说明理由;
(2)若∠ACB=40°,求∠DBE的度数.
参考答案
1.C
2.A
3.D
4.D
5.C
6.C
7.D
8.C
9.D
10.A
11.相等
12.5 4
13.对
14.5 70°
15.96
16.AB和AC,AD和AE,BD和CE
17.△BEC≌△DFC,点B与点D是对应顶点,点C与点C是对应顶点,点E与点F是对应顶点;BC与CD是对应边,BE与DF是对应边,EC与FC是对应边;∠EBC与∠FDC是对应角,∠FCD与∠ECB是对应角,∠BEC与∠DFC是对应角;∠F的度数为70°.
【详解】
∵将△BEC绕点C顺时针旋转90°至△DFC,
∴△BEC≌△DFC,
∴点B与点D是对应顶点,点C与点C是对应顶点,点E与点F是对应顶点,
BC与CD是对应边,BE与DF是对应边,EC与FC是对应边,
∠EBC与∠FDC是对应角,∠FCD与∠ECB是对应角,∠BEC与∠DFC是对应角,
∵∠EBC=30°,∠BCE=80°,
∴∠BEC=180°-30°-80°=70°,
∵△BEC≌△DFC,
∴∠F=∠BEC=70°.
18.(1)见解析;(2)△BCE的周长为18.
【详解】
(1)证明:∵AB=BC,点D是AC边的中点,
∴AD=CD,∠ADB=∠CDE=90°.
又∵DE=BD,
∴△ABD≌△CED(SAS);
(2)解:∵BD=BC2?CD2=52?32=4,
∴BE=2BD=8.
又∵CE=AB=BC=5,
∴BC+CE+BE=5+5+8=18,即△BCE的周长为18.
19.(1)答案见解析;(2) MN=2.1cm,HG=2.2cm.
【详解】
解:(1)对应边:EG和NH,EF和NM;对应角:∠E和∠N,∠EGF和∠NHM.
(2)由△EFG≌△NMH,得MN=EF=2.1 cm,EG=NH=3.3 cm,所以HG=EG-EH=2.2 cm.
20.(1)BE=AD;理由见解析;(2)∠DBE =40°.
【解析】
(1)求出∠BCE=∠ACD,根据SAS证出△BCE≌△ACD,得出对应边相等即可;
(2)由等腰三角形的性质和三角形内角和定理求出∠A=∠ABC=70°,由△BCE≌△ACD,得出对应角相等∠EBC=∠A=70°,再由三角形的外角性质得出∠DBE=∠ACB=40°即可.
解:(1)BE=AD;理由如下:
∵∠ECD=∠BCA,∴∠ECD+∠BCD=∠BCA+∠BCD,∴∠BCE=∠ACD,
在△BCE和△ACD中,,
∴△BCE≌△ACD(SAS),
∴BE=AD.
(2)∵CB=CA,∠ACB=40°,∴∠A=∠ABC=70°,
由(1)得:△BCE≌△ACD,∴∠EBC=∠A=70°,
∵∠DBC=∠DBE+∠EBC=∠ACB+∠ACB,
∴∠DBE=∠ACB=40°.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法正确的是( )
A.两个长方形是全等图形 B.形状相同的两个三角形全等
C.两个全等图形面积一定相等 D.所有的等边三角形都是全等三角形
2.下列说法中,正确的有( )
①正方形都是全等形;②等边三角形都是全等形;③形状相同的图形是全等形;④大小相同的图形是全等形;⑤能够完全重合的图形是全等形.
A.1个 B.2个 C.3个 D.4个
3.如图,在false中,false分别是false上的点,若false,则false的度数是( )
A.false B.false C.false D.false
4.下列四个图形中,全等的图形是( )
A.①和②???????????????? B.①和③ C.②和③ D.③和④
5.下列各组中的两个图形为全等形的是( ).
A.两块三角尺 B.两枚硬币 C.两张 A4 纸 D.两片枫树叶
6.如图,已知△ABC≌△CDE,下列结论中不正确的是( )
A.AC=CE B.∠BAC=∠ECD C.∠ACB=∠ECD D.∠B=∠D
7.下列图形中,是全等图形的是( )
A. B.
C. D.
8.如图,将一张长方形纸片false沿对角线AC折叠后,点D落在点E处,与BC交于点F,图中共有全等三角形()
A.2对 B.3对 C.4对 D.5对
9.下列说法:false两个形状相同的图形称为全等图形;false两个正方形是全等图形;false全等图形的形状、大小都相同;false面积相等的两个三角形是全等图形false其中,正确的是(????)
A.false B.false C.false D.false
10.在锐角△ABC中,∠ABC=60°,BC=2cm,BD平分∠ABC交AC于点D,点M,N分别是BD和BC边上的动点,则MN+MC的最小值是( ).
A.false B.false C.false D.false
二、填空题
11.如果两个图形全等,那么它们的面积________.
12.如图,false,若false ,则false______,false______.
13.若两个三角形全等,那么它们对应的高、中线、角平分线的关系是相等.(____)
14.如图,四边形EFGH与四边形ABCD是全等图形,若AD=5,∠B=70°.则 EH=________?,∠F=________?.
15.如图, 已知△ABC≌△ADC,∠BAC=60°,∠ACD=24°, 那么∠D=________°.
16.如图,△ABD≌△ACE,且∠BAD和∠CAE,∠ABD和∠ACE,∠ADB和∠AEC是对应角,则对应边_________.
三、解答题
17.如图,点false是正方形false内的一点,将false绕点false顺时针旋转90°至false,指出图中的全等图形以及它们的对应顶点、对应边和对应角.若已知false,false,求false的度数.
18.如图,在等腰△ABC中,AB=BC,点D是AC边的中点,延长BD至点E,使得DE=BD,连结CE.
(1)求证:△ABD≌△CED.
(2)当BC=5,CD=3时,求△BCE的周长.
19.如图,点E,H,G,N在同一直线上,△EFG≌△NMH,∠F和∠M是对应角.在△EFG中,FG是最长边.在△NMH中,MH是最长边.已知EF=2.1 cm,EH=1.1 cm,HN=3.3 cm.
(1)写出其他对应边及对应角;
(2)求线段MN及线段HG的长度.
20.如图,在等腰△ABC中,CB=CA,延长AB至点D,使DB=CB,连接CD,以CD为边作等腰△CDE,使CE=CD,∠ECD=∠BCA,连接BE交CD于点M.
(1)BE=AD吗?请说明理由;
(2)若∠ACB=40°,求∠DBE的度数.
参考答案
1.C
2.A
3.D
4.D
5.C
6.C
7.D
8.C
9.D
10.A
11.相等
12.5 4
13.对
14.5 70°
15.96
16.AB和AC,AD和AE,BD和CE
17.△BEC≌△DFC,点B与点D是对应顶点,点C与点C是对应顶点,点E与点F是对应顶点;BC与CD是对应边,BE与DF是对应边,EC与FC是对应边;∠EBC与∠FDC是对应角,∠FCD与∠ECB是对应角,∠BEC与∠DFC是对应角;∠F的度数为70°.
【详解】
∵将△BEC绕点C顺时针旋转90°至△DFC,
∴△BEC≌△DFC,
∴点B与点D是对应顶点,点C与点C是对应顶点,点E与点F是对应顶点,
BC与CD是对应边,BE与DF是对应边,EC与FC是对应边,
∠EBC与∠FDC是对应角,∠FCD与∠ECB是对应角,∠BEC与∠DFC是对应角,
∵∠EBC=30°,∠BCE=80°,
∴∠BEC=180°-30°-80°=70°,
∵△BEC≌△DFC,
∴∠F=∠BEC=70°.
18.(1)见解析;(2)△BCE的周长为18.
【详解】
(1)证明:∵AB=BC,点D是AC边的中点,
∴AD=CD,∠ADB=∠CDE=90°.
又∵DE=BD,
∴△ABD≌△CED(SAS);
(2)解:∵BD=BC2?CD2=52?32=4,
∴BE=2BD=8.
又∵CE=AB=BC=5,
∴BC+CE+BE=5+5+8=18,即△BCE的周长为18.
19.(1)答案见解析;(2) MN=2.1cm,HG=2.2cm.
【详解】
解:(1)对应边:EG和NH,EF和NM;对应角:∠E和∠N,∠EGF和∠NHM.
(2)由△EFG≌△NMH,得MN=EF=2.1 cm,EG=NH=3.3 cm,所以HG=EG-EH=2.2 cm.
20.(1)BE=AD;理由见解析;(2)∠DBE =40°.
【解析】
(1)求出∠BCE=∠ACD,根据SAS证出△BCE≌△ACD,得出对应边相等即可;
(2)由等腰三角形的性质和三角形内角和定理求出∠A=∠ABC=70°,由△BCE≌△ACD,得出对应角相等∠EBC=∠A=70°,再由三角形的外角性质得出∠DBE=∠ACB=40°即可.
解:(1)BE=AD;理由如下:
∵∠ECD=∠BCA,∴∠ECD+∠BCD=∠BCA+∠BCD,∴∠BCE=∠ACD,
在△BCE和△ACD中,,
∴△BCE≌△ACD(SAS),
∴BE=AD.
(2)∵CB=CA,∠ACB=40°,∴∠A=∠ABC=70°,
由(1)得:△BCE≌△ACD,∴∠EBC=∠A=70°,
∵∠DBC=∠DBE+∠EBC=∠ACB+∠ACB,
∴∠DBE=∠ACB=40°.
