高中物理人教版(2019)必修 第二册第六章 6.4生活中的圆周运动(共25张PPT)
文档属性
| 名称 | 高中物理人教版(2019)必修 第二册第六章 6.4生活中的圆周运动(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-18 10:20:40 | ||
图片预览




文档简介
(共25张PPT)
第六章
圆周运动
6.4生活中的圆周运动(一)
学习目标
1.进一步分析向心力的来源,会利用牛顿第二定律结合匀速圆周运动的规律处理火车转弯、汽车转弯问题;
2.明确圆周运动问题中的“供求”关系,理解离心和向心现象的产生原因。
问题反馈
1.轨道内、外侧同高,为什么外侧会产生力使火车转弯?外轨高于内轨会不会挤压内轨,此时FN与G的合力为火车提供了一部分向心力如何理解?
2.火车转弯向心力的来源,火车转弯时有限速吗?如何求。若有当大于或小于这个限速时会怎样。
3.汽车过拱形桥时为什么FN与G
不相等,过桥时速度对压力的影响是什么?在公式FN=mg-mv2/R中,V越大是否存在FN=0的情况?此时车会怎样运动?
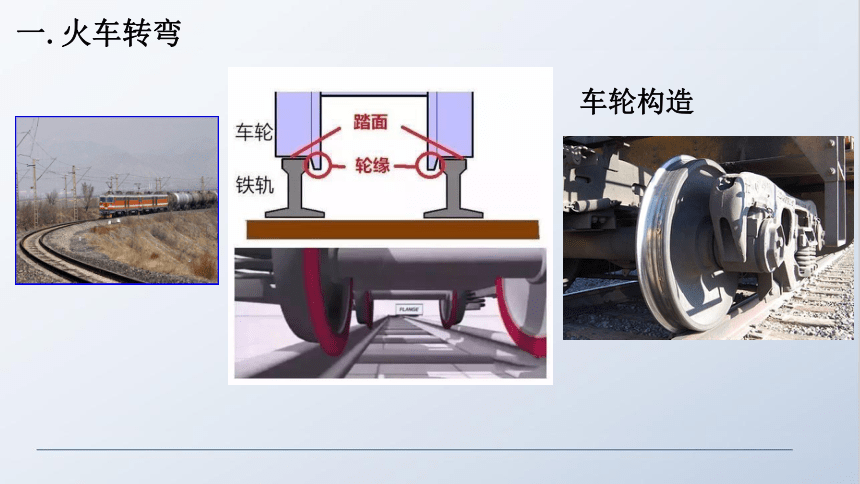
一.火车转弯
车轮构造
思考:
1.火车转弯时,若弯道水平,向心力由什么提供?
2.实际的铁路弯道处总是外轨略高于内轨,此时火车的向心力又由什么提供?
3.若路基的倾角为θ,则其转弯时速度多大时轮缘与轨道刚好无挤压?
4.若转弯时实际车速大于或小于规定车速时,情况如何?
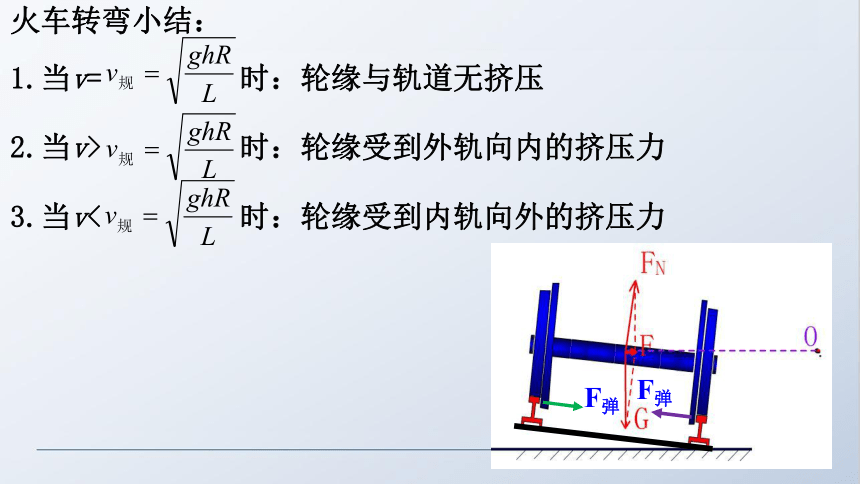
1.当v=
时:轮缘与轨道无挤压
2.当v>
时:轮缘受到外轨向内的挤压力
3.当v<
时:轮缘受到内轨向外的挤压力
F弹
F弹
火车转弯小结:
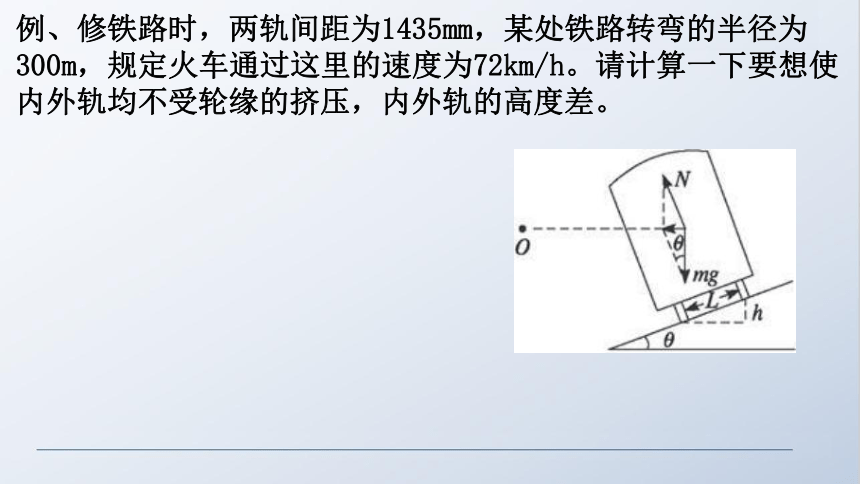
例、修铁路时,两轨间距为1435mm,某处铁路转弯的半径为300m,规定火车通过这里的速度为72km/h。请计算一下要想使内外轨均不受轮缘的挤压,内外轨的高度差。
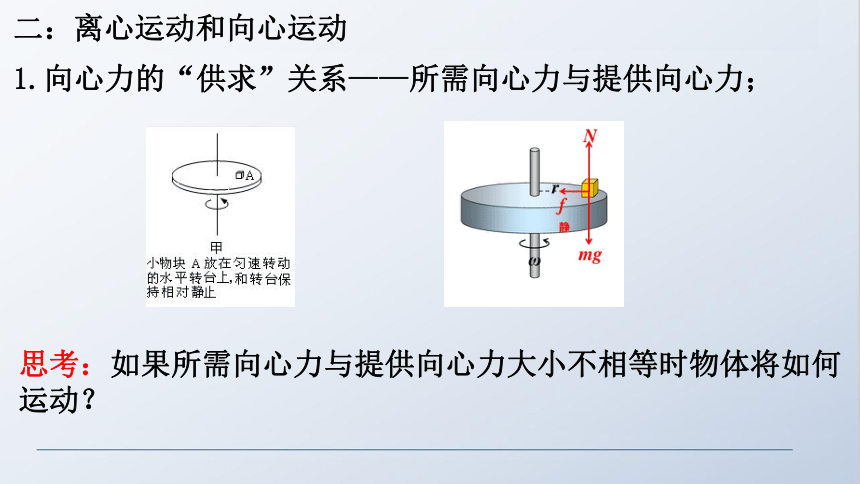
二:离心运动和向心运动
1.向心力的“供求”关系——所需向心力与提供向心力;
思考:如果所需向心力与提供向心力大小不相等时物体将如何运动?
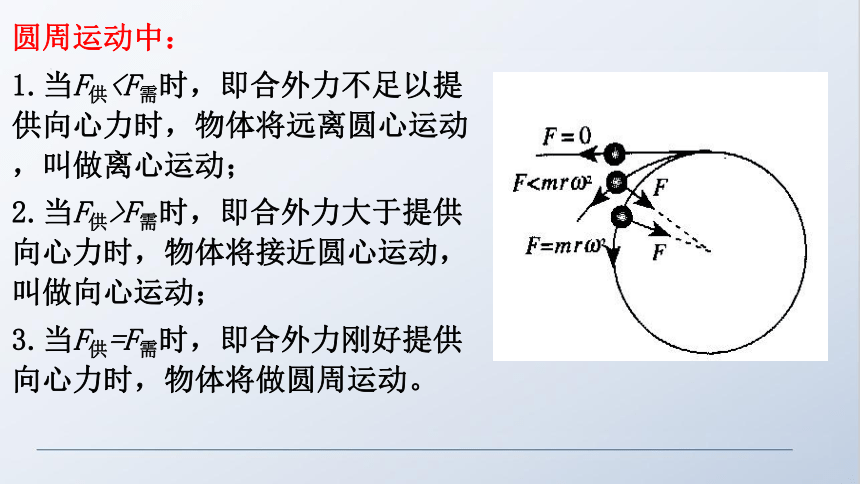
圆周运动中:
1.当F供2.当F供>F需时,即合外力大于提供向心力时,物体将接近圆心运动,叫做向心运动;
3.当F供=F需时,即合外力刚好提供向心力时,物体将做圆周运动。
小结:
2.离心现象的应用及防止
小结
1.处理火车转弯、汽车转弯问题关键是找到向心力的来源;
2.圆周运动问题中的“供求”关系,离心和向心现象的产生原因。
第六章
圆周运动
6.4生活中的圆周运动(二)
学习目标
1.知道竖直面内圆周运动的物体其受力特点和运动规律,能准确对最高点和最低点列出动力学方程。
2.会分析绳模型、杆模型中最高点处弹力的临界问题,明确各模型中过最高点的条件。
3.体会牛顿运动定律在圆周运动问题中的应用。
一.拱形桥及圆周运动中的超重失重现象
1.汽车在拱形桥最高点处的向心力由什么力提供?
2.若汽车通过最高点处时的速度变大,则它对桥的压力如何变化?
3.汽车速度为多大时,在最高点对桥的压力正好为0?(假设桥的半径为R)如果车速大于这个速度会怎样?
4.若汽车通过拱形桥最高点处和凹形桥的最低点时,处于超重还是失重?
FN
mg
例.地球可以看作一座巨大的拱形桥,其半径为地球半径R(约为6400km),若地面上的汽车不断加速,速度达到多大时,地面对汽车的支持力会为0?这时汽车中的驾驶员所受到汽车的支持力又如何?
二.绳模型
o
v
用细绳系着一重物,用手提着另一端,你能让透明胶带在竖直平面内能做完整的圆周运动吗?如果让重物的速度再小一些呢?试试看此完整的圆周运动最不易通过的点在什么地方?
思考:
1.小球在最高点的受力情况如何?谁提供向心力?2.小球在最高点的速度变小,绳的拉力怎么变?速度为多大时,绳上拉力正好为0?
3.小球过最高点速度大于或小于
时,分别对应什么现象?小球能过最高点的条件是什么?
4.小球运动到最低点谁来提供向心力?小球在哪个位置所受的拉力(或轨道支持力)最大?
o
v
在光滑圆环内运动的小球等效于绳模型
光滑圆环
1.(多选)在乘坐游乐园的过山车时,质量为m的人随车在竖直平面内沿圆周轨道运动,如图所示,下列说法正确的是( )。
A.车在最高点时人处于倒坐状态,全靠保险带拉住,若没有保险带,人一定会掉下去
B.人在最高点时对座位仍可能产生压力,但压力一定小于mg
C.人在最低点时处于超重状态
D.人在最低点时对座位的压力大于mg
2.绳系着装有水的水桶,在竖直平面内作圆周运动,水的质量m=0.5kg,绳长L=90cm,g=10m/s2.求:
(1)最高点水不流出的最小速率?
(2)水在最高点v=6m/s时,水对桶底的压力?
v2
如果让长为L的轻杆一端固定着一质量为m的小球,使小球在竖直平面内做圆周运动。
思考:
1.设小球在最低点A的速度为v1,谁来提供向心力?小球的受力与速度的关系是如何?
2.设小球在最高点B的速度为v2,谁来提供向心力?小球的受力与速度的关系又是如何?3.要使小球能在竖直平面内做圆周运动,最高点的速度满足什么条件?
A
B
v1
三.杆模型
在光滑圆管道内运动的小球等效于杆模型
v
v
光滑圆管
3.长L=0.5
m的轻杆,其一端连接着一个物体A,A的质量m=2
kg。现让A在竖直平面内绕O点做匀速圆周运动,如图所示。在A通过最高点时,求下列两种情况下A对杆的作用力。(g=10
m/s2)
(1)A的速率为1
m/s;
(2)A的速率为4
m/s。
课堂总结:
拱桥模型
绳模型
杆模型
弹力方向
向上
(只可支撑)
向下
(只可下拉)
向上或向下
(可支撑,可下拉)
能过最高点的条件
第六章
圆周运动
6.4生活中的圆周运动(一)
学习目标
1.进一步分析向心力的来源,会利用牛顿第二定律结合匀速圆周运动的规律处理火车转弯、汽车转弯问题;
2.明确圆周运动问题中的“供求”关系,理解离心和向心现象的产生原因。
问题反馈
1.轨道内、外侧同高,为什么外侧会产生力使火车转弯?外轨高于内轨会不会挤压内轨,此时FN与G的合力为火车提供了一部分向心力如何理解?
2.火车转弯向心力的来源,火车转弯时有限速吗?如何求。若有当大于或小于这个限速时会怎样。
3.汽车过拱形桥时为什么FN与G
不相等,过桥时速度对压力的影响是什么?在公式FN=mg-mv2/R中,V越大是否存在FN=0的情况?此时车会怎样运动?
一.火车转弯
车轮构造
思考:
1.火车转弯时,若弯道水平,向心力由什么提供?
2.实际的铁路弯道处总是外轨略高于内轨,此时火车的向心力又由什么提供?
3.若路基的倾角为θ,则其转弯时速度多大时轮缘与轨道刚好无挤压?
4.若转弯时实际车速大于或小于规定车速时,情况如何?
1.当v=
时:轮缘与轨道无挤压
2.当v>
时:轮缘受到外轨向内的挤压力
3.当v<
时:轮缘受到内轨向外的挤压力
F弹
F弹
火车转弯小结:
例、修铁路时,两轨间距为1435mm,某处铁路转弯的半径为300m,规定火车通过这里的速度为72km/h。请计算一下要想使内外轨均不受轮缘的挤压,内外轨的高度差。
二:离心运动和向心运动
1.向心力的“供求”关系——所需向心力与提供向心力;
思考:如果所需向心力与提供向心力大小不相等时物体将如何运动?
圆周运动中:
1.当F供
3.当F供=F需时,即合外力刚好提供向心力时,物体将做圆周运动。
小结:
2.离心现象的应用及防止
小结
1.处理火车转弯、汽车转弯问题关键是找到向心力的来源;
2.圆周运动问题中的“供求”关系,离心和向心现象的产生原因。
第六章
圆周运动
6.4生活中的圆周运动(二)
学习目标
1.知道竖直面内圆周运动的物体其受力特点和运动规律,能准确对最高点和最低点列出动力学方程。
2.会分析绳模型、杆模型中最高点处弹力的临界问题,明确各模型中过最高点的条件。
3.体会牛顿运动定律在圆周运动问题中的应用。
一.拱形桥及圆周运动中的超重失重现象
1.汽车在拱形桥最高点处的向心力由什么力提供?
2.若汽车通过最高点处时的速度变大,则它对桥的压力如何变化?
3.汽车速度为多大时,在最高点对桥的压力正好为0?(假设桥的半径为R)如果车速大于这个速度会怎样?
4.若汽车通过拱形桥最高点处和凹形桥的最低点时,处于超重还是失重?
FN
mg
例.地球可以看作一座巨大的拱形桥,其半径为地球半径R(约为6400km),若地面上的汽车不断加速,速度达到多大时,地面对汽车的支持力会为0?这时汽车中的驾驶员所受到汽车的支持力又如何?
二.绳模型
o
v
用细绳系着一重物,用手提着另一端,你能让透明胶带在竖直平面内能做完整的圆周运动吗?如果让重物的速度再小一些呢?试试看此完整的圆周运动最不易通过的点在什么地方?
思考:
1.小球在最高点的受力情况如何?谁提供向心力?2.小球在最高点的速度变小,绳的拉力怎么变?速度为多大时,绳上拉力正好为0?
3.小球过最高点速度大于或小于
时,分别对应什么现象?小球能过最高点的条件是什么?
4.小球运动到最低点谁来提供向心力?小球在哪个位置所受的拉力(或轨道支持力)最大?
o
v
在光滑圆环内运动的小球等效于绳模型
光滑圆环
1.(多选)在乘坐游乐园的过山车时,质量为m的人随车在竖直平面内沿圆周轨道运动,如图所示,下列说法正确的是( )。
A.车在最高点时人处于倒坐状态,全靠保险带拉住,若没有保险带,人一定会掉下去
B.人在最高点时对座位仍可能产生压力,但压力一定小于mg
C.人在最低点时处于超重状态
D.人在最低点时对座位的压力大于mg
2.绳系着装有水的水桶,在竖直平面内作圆周运动,水的质量m=0.5kg,绳长L=90cm,g=10m/s2.求:
(1)最高点水不流出的最小速率?
(2)水在最高点v=6m/s时,水对桶底的压力?
v2
如果让长为L的轻杆一端固定着一质量为m的小球,使小球在竖直平面内做圆周运动。
思考:
1.设小球在最低点A的速度为v1,谁来提供向心力?小球的受力与速度的关系是如何?
2.设小球在最高点B的速度为v2,谁来提供向心力?小球的受力与速度的关系又是如何?3.要使小球能在竖直平面内做圆周运动,最高点的速度满足什么条件?
A
B
v1
三.杆模型
在光滑圆管道内运动的小球等效于杆模型
v
v
光滑圆管
3.长L=0.5
m的轻杆,其一端连接着一个物体A,A的质量m=2
kg。现让A在竖直平面内绕O点做匀速圆周运动,如图所示。在A通过最高点时,求下列两种情况下A对杆的作用力。(g=10
m/s2)
(1)A的速率为1
m/s;
(2)A的速率为4
m/s。
课堂总结:
拱桥模型
绳模型
杆模型
弹力方向
向上
(只可支撑)
向下
(只可下拉)
向上或向下
(可支撑,可下拉)
能过最高点的条件
