三角形内切圆

(共18张PPT)
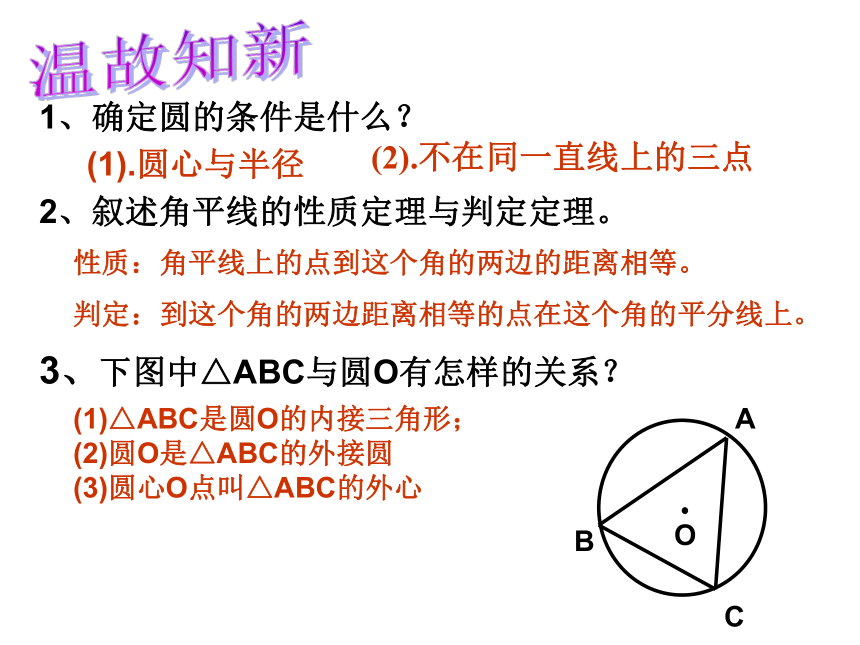
1、确定圆的条件是什么？
(1).圆心与半径
2、叙述角平线的性质定理与判定定理。
性质：角平线上的点到这个角的两边的距离相等。
判定：到这个角的两边距离相等的点在这个角的平分线上。
(2).不在同一直线上的三点
(1)△ABC是圆O的内接三角形；
(2)圆O是△ABC的外接圆
(3)圆心O点叫△ABC的外心
A
C
B
O
3、下图中△ABC与圆O有怎样的关系？
探索与思考
如图是一张三角形的铁皮，工人师傅要从中截下一块圆形的用料，怎样才能使截下的圆的面积尽可能大呢？
A
B
C
A
B
C
A
B
C
A
B
C
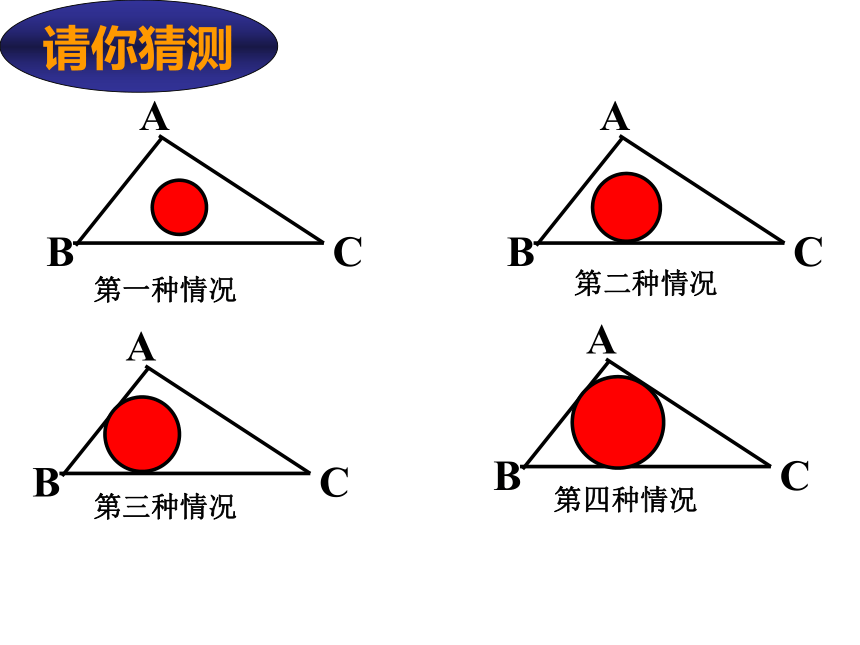
请你猜测
第一种情况
第二种情况
第三种情况
第四种情况
A
B
C
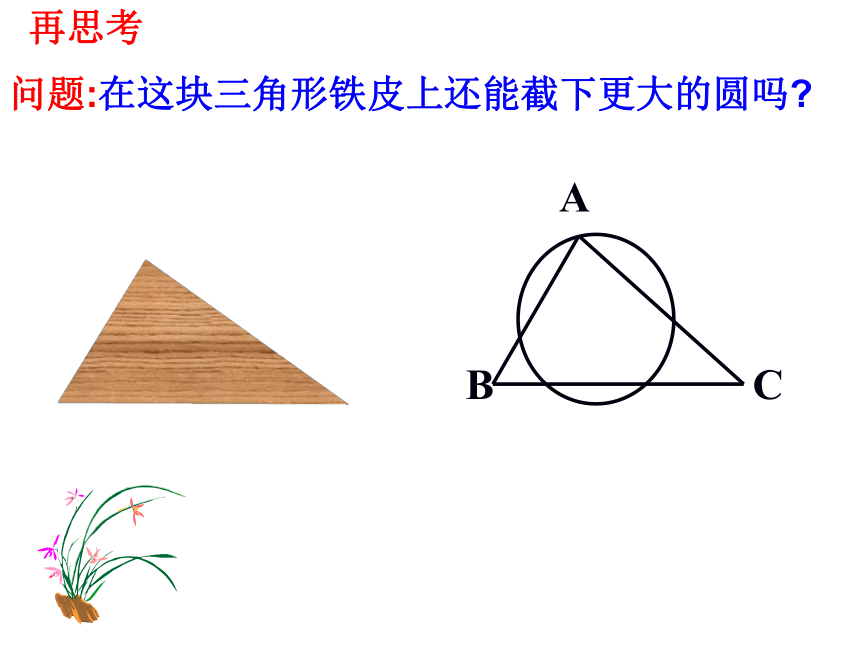
再思考
问题:在这块三角形铁皮上还能截下更大的圆吗
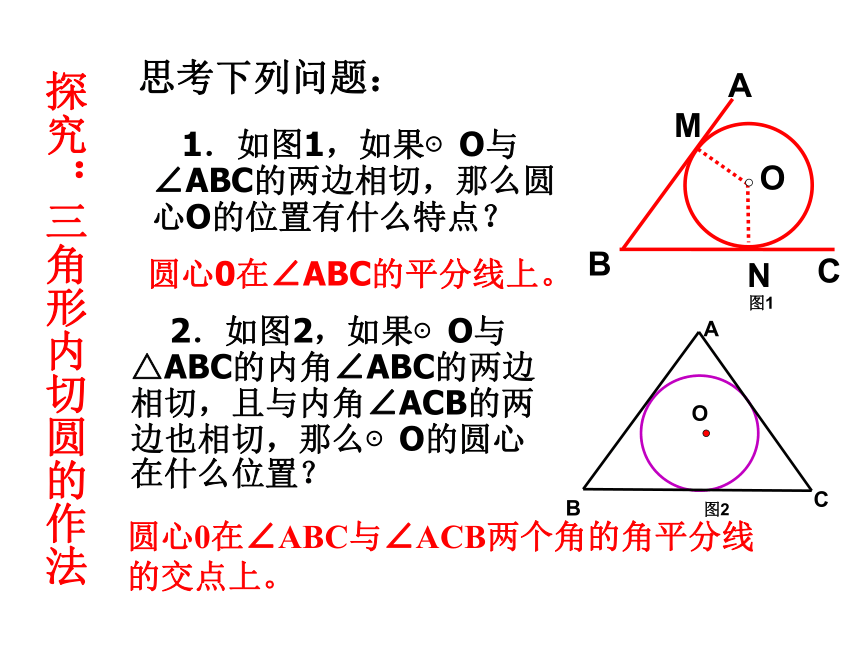
思考下列问题：
1．如图1，如果⊙O与∠ABC的两边相切，那么圆心O的位置有什么特点？
圆心0在∠ABC的平分线上。
2．如图2，如果⊙O与△ABC的内角∠ABC的两边相切，且与内角∠ACB的两边也相切，那么⊙O的圆心在什么位置？
圆心0在∠ABC与∠ACB两个角的角平分线的交点上。
O
M
A
B
C
N
O
图2
A
B
C
探究：三角形内切圆的作法
图1
3．如何确定一个与三角形的三边都相切的圆的圆心的位置与半径的长？
4．你能作出几个与一个三角形的三边都相切的圆？
作出三个内角的平分线，三条内角
平分线相交于一点，这个点就是符合
条件的圆心，过圆心作一边的垂线，
垂线段的长是符合条件的半径。
只能作一个，因为三角形的三条内角
平分线相交只有一个交点。
I
F
C
A
B
E
D
探究：三角形内切圆的作法
探究：三角形内切圆的作法
M
N
D
作法：
1、作∠B、∠C的平分线BM和 CN，交点为O。
2、过点O作OD⊥BC，垂足为D。
3、以O为圆心，OD为半径作⊙O.
⊙O就是所求的圆。
和三角形各边都相切的圆叫三角形的内切圆
三角形叫圆的外切三角形
1、作三角形的内切圆的步骤:
作角平分线→定内心→定半径→作圆
2、定义：和三角形各边都相切的圆叫做三角形的内切圆，
内切圆的圆心叫做三角形的内心，
这个三角形叫做圆的外切三角形。
3、三角形内心的性质
①三角形的内心是三角形角平分线的交点
②三角形的内心到三边的距离相等
③三角形的内心一定在三角形的内部
④内心与顶点连线平分内角。
我能行
判断题：
1.三角形的内心到三角形各个顶点的距离相等.( )
2.三角形的外心到三角形各边的距离相等.( )
3.等边三角形的内心和外心重合. ( )
4.三角形的内心一定在三角形的内部. ( )
错
错
对
对
图形 圆心的确定方法 圆心名称 性质
三角形三边垂
直平分线的
交点
1.OA=OB=OC
2.外心不一定在三角形的内部．
三角形三个
内角平分
线的交点
1.内心到三角形三边的距离相等；
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心一定在三角形内部．
三角形的外接圆与内切圆比较
外心：三角
形外接圆
的圆心
内心：三角
形内切圆
的圆心
如图，在△ABC中，∠ABC=50°，
∠ACB＝75°，点O是内心，求∠BOC
的度数。
∠BO C=
∠1 + ∠3=
O为△ABC的内心
BO是∠ABC的角平分线
CO是∠ACB的角平分线
分析：
O
A
2
4
3
B
C
1
解 ：∵点O为△ABC的内心
∴∠1＝∠2＝
∴ ∠BOC=1800 - (∠1+∠3)
=1800 - (250+37.50)
=117.50
∴ ∠BOC=117.50
C
1
O
2
4
3
B
A
三角形内心性质的应用
O
A
2
4
3
B
C
1
变式1：在△ABC中，点O是内心，
∠BAC=50°，求∠BOC的度数。
变式2：在△ABC中，点O是内心，
∠BOC=120°，求∠BAC的度数。
试探讨∠BOC与∠A之间存在怎样的数量关系？
请说明理由．
1
∠BOC =90 °
∠A
2
+
精彩源于发现
2
∠BOC=180°﹣
1
2
(∠ABC+∠ACB)
=180°-
1
2
(180°-∠A)
=180°-90°+
1
2
∠A
=90°+
1
∠A
驶向胜利的彼岸
三角形内切圆的做法.
三角形内心，圆的外切三角形的概念.
三角形内心到三角形三边距离相等.
学会了用代数方法解决几何问题.
思想方法：类比的思想方法；利用三角形内心的性质解题时，要注意整体思想的运用；在解决实际问题时，要注意把实际问题转化为数学问题。