4.3.3 余角和补角 课件(共25张PPT)
文档属性
| 名称 | 4.3.3 余角和补角 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-20 20:22:01 | ||
图片预览




文档简介
(共25张PPT)
4.3.3
余角和补角
人教版本
七年级
1.
了解余角、补角的概念,掌握余角和补角的性质,
并能利用余角、补角的知识解决相关问题.(重点、
难点)
2.
了解方位角的概念,并能用方位角知识解决一些
简单的实际问题.(难点)
教学目标
新知导入
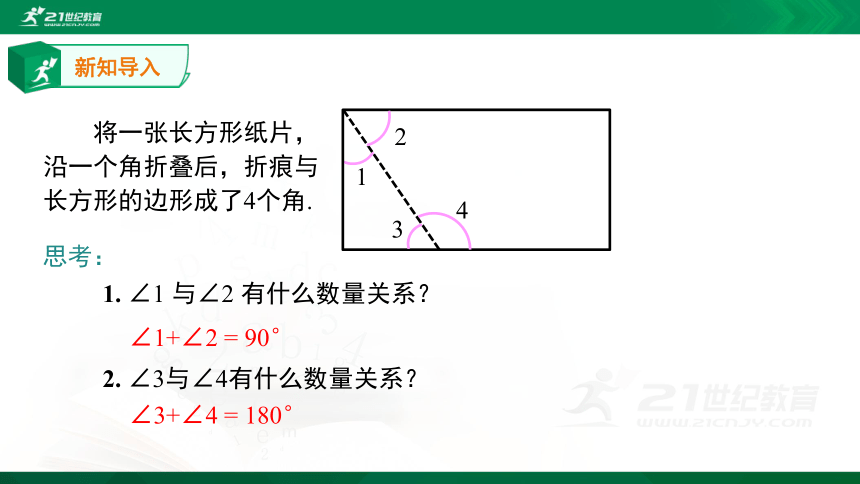
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
1
2
3
4
思考:
1.
∠1
与∠2
有什么数量关系?
∠1+∠2
=
90°
2.
∠3与∠4有什么数量关系?
∠3+∠4
=
180°
新知讲解
1
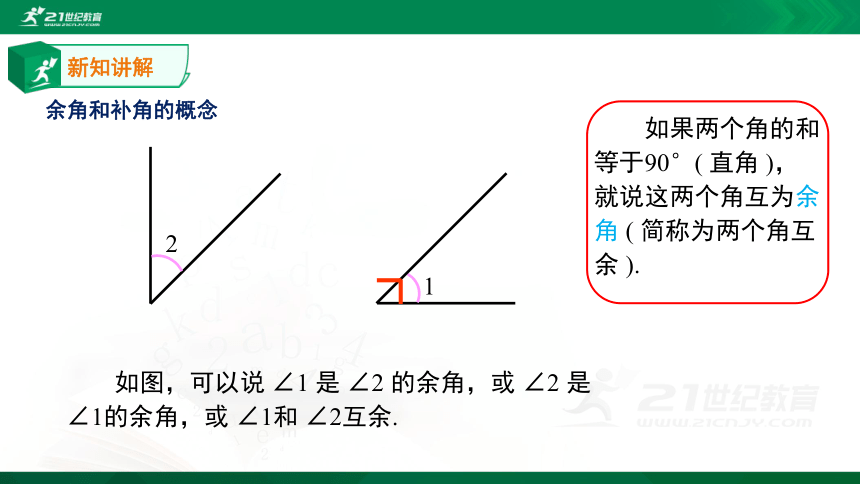
如果两个角的和等于90°(
直角
),就说这两个角互为余角
(
简称为两个角互余
).
如图,可以说
∠1
是
∠2
的余角,或
∠2
是
∠1的余角,或
∠1和
∠2互余.
2
余角和补角的概念
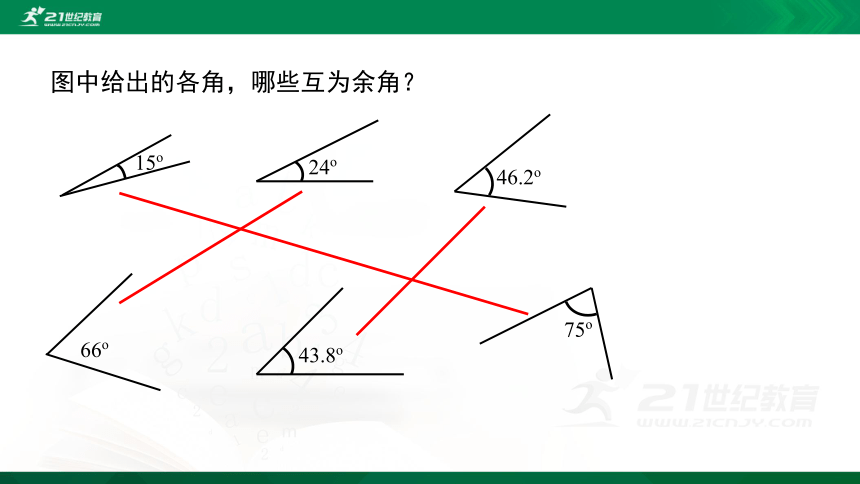
图中给出的各角,哪些互为余角?
15o
24o
66o
75o
46.2o
43.8o
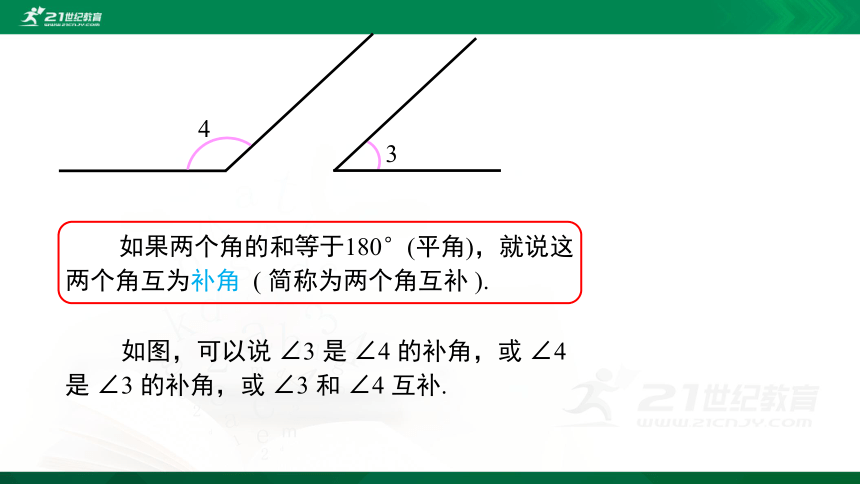
如果两个角的和等于180°(平角),就说这两个角互为补角
(
简称为两个角互补
).
如图,可以说
∠3
是
∠4
的补角,或
∠4是
∠3
的补角,或
∠3
和
∠4
互补.
4
3
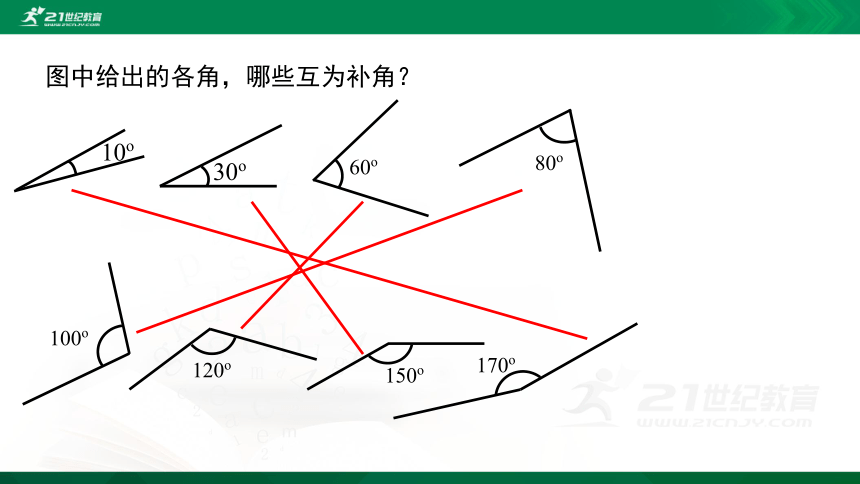
图中给出的各角,哪些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
例题讲解
例1
若一个角的补角等于它的余角的
4
倍,求这个角的度数.
解:设这个角为
x°,则它的补角是
(
180-x
)°,
余角是
(
90-x
)°
.
根据题意,得
180-x
=
4
(
90-x
)
.
解得
x
=
60.
答:这个角的度数是
60
°.
练一练
已知
∠A
与∠B
互余,且
∠A
的度数比∠B
度数的
3
倍还多30°,求∠B的度数.
解:设∠B的度数为x°,则
∠A
的度数为
(3x+30)°.
根据题意得:
x
+
(
3x+30
)
=
90.
解得
x=15.
故
∠B
的度数为15°.
例3
如图,点A,O,B在同一直线上,射线
OD
和射线
OE
分别平分∠AOC
和∠BOC,图中哪些角互为余角?
解:因为点A,O,B在同一直线
上,所以
∠AOC
和
∠BOC
互为补角.
O
A
B
C
D
E
又因为射线
OD
和射线
OE
分别平分∠AOC
和∠BOC,所以∠COD+∠COE=
∠AOC+
∠BOC
=
(∠AOC+∠BOC
)
=
90°.
O
A
B
C
D
E
所以∠COD和∠COE互为余角,
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
观看下列视频,议一议其中蕴含的数学知识.
新知讲解
方位角
东
西
北
南
O
正东:
正南:
正西:
正北:
西北方向:
西南方向:
东北方向:
东南方向:
射线
OA
A
B
C
D
45°
E
G
F
H
45°
八大方位
45°
45°
射线
OB
射线
OC
射线
OD
射线
OE
射线
OF
射线
OH
射线
OG
45°
如图,说出下列方位
(1)
射线
OA
表示的方向
为
.
(2)
射线
OB
表示的方向
为
___
_
.
(3)
射线
OC
表示的方向
为
.
(4)
射线
OD
表示的方向
为
.
北
东
西
南
C
A
B
D
北偏东
40°
北偏西
65°
南偏西
45°(西南)
南偏东
20°
40°
65°
70°
O
20°
例4
如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上.
同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)
方向上又分别发现了客
轮B,货轮C和海岛D.
仿照表示灯塔方位的
方法画出表示客轮B,
货轮C和海岛D方向的
射线.
东
南
西
北
60°
●
B
40°
10°
45°
C
●
●
A
●
D
O
●
费俊龙、聂海胜乘坐“神舟”六号遨游太空时,我国当时派出远望一号~四号船队,跟踪检测.
其中远望一、二号停在太平洋洋面上,某一时刻,分别测得神舟六号在北偏东60°和北偏东30°的方向,你能在下图中画出当时神舟六号所处的位置吗?
●
●
远望一号
远望二号
练一练
●
●
远望一号
远望二号
60°
30°
●
1.一个角的余角是它的2倍,这个角的度数是( )
A.30°
B.45°
C.60°
D.75°
A
2.下列说法正确的是( )
A.一个角的补角一定大于它本身
B.一个角的余角一定小于它本身
C.一个钝角减去一个锐角的差一定是一个锐角
D.一个角的余角一定小于其补角
D
课堂练习
3.已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,则∠C的度数是_______.
150°
4.
∠1
与
∠2
互余,∠1
=
(6x
+
8)°,∠2
=
(4x-8)°,
则∠1=
,∠2=
.
62°
28°
5.
如图,已知∠ACB=∠CDB=90°.
(1)
图中有哪几对互余的角?
(2)
图中哪几对角是相等的角(直角除外)?为什么?
答案:∠A+∠B=90°
∠A+∠2=90°
∠1+∠B=90°
∠1+∠2=90°
答案:∠B=∠2
∠A=∠1
(
同角的余角相等
)
(
同角的余角相等
)
A
C
D
1
2
B
60°
30°
6.
垃圾打捞船
A
和
B
都停驻在湖边观测湖面,从
A
船发现它的北偏东60°方向有白色漂浮物,
同时,从
B
船也发现该白色漂浮物在它的北偏
西30°方向.
(1)
试在图中确定白色漂浮物C的位置;
A
B
北
北
C
60°
北
A.
南偏东30°
B.
南偏西30°
C.
南偏东60°
D.
南偏西60°
(2)
点
C
在点
A
的北偏东60°的方向上,那么点
A
在点
C
的______方向上.
60°
30°
A
B
北
北
C
D
课堂小结
同角或等角的
补角相等
同角或等角的
余角相等
互余
互补
两角间的数量关系
性质
方位角
物体运动的方向与正北、正南方向之间的夹角称为方位角,一般以正北、正南为基准,用向东或向西旋转的角度表示方向
定义
书写
通常要先写北或南,再写偏东或偏西
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
4.3.3
余角和补角
人教版本
七年级
1.
了解余角、补角的概念,掌握余角和补角的性质,
并能利用余角、补角的知识解决相关问题.(重点、
难点)
2.
了解方位角的概念,并能用方位角知识解决一些
简单的实际问题.(难点)
教学目标
新知导入
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
1
2
3
4
思考:
1.
∠1
与∠2
有什么数量关系?
∠1+∠2
=
90°
2.
∠3与∠4有什么数量关系?
∠3+∠4
=
180°
新知讲解
1
如果两个角的和等于90°(
直角
),就说这两个角互为余角
(
简称为两个角互余
).
如图,可以说
∠1
是
∠2
的余角,或
∠2
是
∠1的余角,或
∠1和
∠2互余.
2
余角和补角的概念
图中给出的各角,哪些互为余角?
15o
24o
66o
75o
46.2o
43.8o
如果两个角的和等于180°(平角),就说这两个角互为补角
(
简称为两个角互补
).
如图,可以说
∠3
是
∠4
的补角,或
∠4是
∠3
的补角,或
∠3
和
∠4
互补.
4
3
图中给出的各角,哪些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
例题讲解
例1
若一个角的补角等于它的余角的
4
倍,求这个角的度数.
解:设这个角为
x°,则它的补角是
(
180-x
)°,
余角是
(
90-x
)°
.
根据题意,得
180-x
=
4
(
90-x
)
.
解得
x
=
60.
答:这个角的度数是
60
°.
练一练
已知
∠A
与∠B
互余,且
∠A
的度数比∠B
度数的
3
倍还多30°,求∠B的度数.
解:设∠B的度数为x°,则
∠A
的度数为
(3x+30)°.
根据题意得:
x
+
(
3x+30
)
=
90.
解得
x=15.
故
∠B
的度数为15°.
例3
如图,点A,O,B在同一直线上,射线
OD
和射线
OE
分别平分∠AOC
和∠BOC,图中哪些角互为余角?
解:因为点A,O,B在同一直线
上,所以
∠AOC
和
∠BOC
互为补角.
O
A
B
C
D
E
又因为射线
OD
和射线
OE
分别平分∠AOC
和∠BOC,所以∠COD+∠COE=
∠AOC+
∠BOC
=
(∠AOC+∠BOC
)
=
90°.
O
A
B
C
D
E
所以∠COD和∠COE互为余角,
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
观看下列视频,议一议其中蕴含的数学知识.
新知讲解
方位角
东
西
北
南
O
正东:
正南:
正西:
正北:
西北方向:
西南方向:
东北方向:
东南方向:
射线
OA
A
B
C
D
45°
E
G
F
H
45°
八大方位
45°
45°
射线
OB
射线
OC
射线
OD
射线
OE
射线
OF
射线
OH
射线
OG
45°
如图,说出下列方位
(1)
射线
OA
表示的方向
为
.
(2)
射线
OB
表示的方向
为
___
_
.
(3)
射线
OC
表示的方向
为
.
(4)
射线
OD
表示的方向
为
.
北
东
西
南
C
A
B
D
北偏东
40°
北偏西
65°
南偏西
45°(西南)
南偏东
20°
40°
65°
70°
O
20°
例4
如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上.
同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)
方向上又分别发现了客
轮B,货轮C和海岛D.
仿照表示灯塔方位的
方法画出表示客轮B,
货轮C和海岛D方向的
射线.
东
南
西
北
60°
●
B
40°
10°
45°
C
●
●
A
●
D
O
●
费俊龙、聂海胜乘坐“神舟”六号遨游太空时,我国当时派出远望一号~四号船队,跟踪检测.
其中远望一、二号停在太平洋洋面上,某一时刻,分别测得神舟六号在北偏东60°和北偏东30°的方向,你能在下图中画出当时神舟六号所处的位置吗?
●
●
远望一号
远望二号
练一练
●
●
远望一号
远望二号
60°
30°
●
1.一个角的余角是它的2倍,这个角的度数是( )
A.30°
B.45°
C.60°
D.75°
A
2.下列说法正确的是( )
A.一个角的补角一定大于它本身
B.一个角的余角一定小于它本身
C.一个钝角减去一个锐角的差一定是一个锐角
D.一个角的余角一定小于其补角
D
课堂练习
3.已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,则∠C的度数是_______.
150°
4.
∠1
与
∠2
互余,∠1
=
(6x
+
8)°,∠2
=
(4x-8)°,
则∠1=
,∠2=
.
62°
28°
5.
如图,已知∠ACB=∠CDB=90°.
(1)
图中有哪几对互余的角?
(2)
图中哪几对角是相等的角(直角除外)?为什么?
答案:∠A+∠B=90°
∠A+∠2=90°
∠1+∠B=90°
∠1+∠2=90°
答案:∠B=∠2
∠A=∠1
(
同角的余角相等
)
(
同角的余角相等
)
A
C
D
1
2
B
60°
30°
6.
垃圾打捞船
A
和
B
都停驻在湖边观测湖面,从
A
船发现它的北偏东60°方向有白色漂浮物,
同时,从
B
船也发现该白色漂浮物在它的北偏
西30°方向.
(1)
试在图中确定白色漂浮物C的位置;
A
B
北
北
C
60°
北
A.
南偏东30°
B.
南偏西30°
C.
南偏东60°
D.
南偏西60°
(2)
点
C
在点
A
的北偏东60°的方向上,那么点
A
在点
C
的______方向上.
60°
30°
A
B
北
北
C
D
课堂小结
同角或等角的
补角相等
同角或等角的
余角相等
互余
互补
两角间的数量关系
性质
方位角
物体运动的方向与正北、正南方向之间的夹角称为方位角,一般以正北、正南为基准,用向东或向西旋转的角度表示方向
定义
书写
通常要先写北或南,再写偏东或偏西
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
