6.2平面向量的运算-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册学案Word
文档属性
| 名称 | 6.2平面向量的运算-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册学案Word |

|
|
| 格式 | docx | ||
| 文件大小 | 232.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-19 19:05:16 | ||
图片预览



文档简介
①、了解平面向量的运算
②、掌握向量线性运算的综合应用
③、理解平面向量的数量积求夹角与积求长度
一、向量的加法运算
1.定义:求两个向量和的运算,叫做向量的加法
2.向量加法的方法:向量加法的三角法则
已知非零向量,在平面内任取一点A,做=,=,则向量叫做与的和,记作,即,这种求向量和的方法,称为向量加法的三角形法则
三角形法则的使用条件:一个向量的终点为另一个向量的起点
平行四边形法则
以同一O为起点的两个已知向量,,以,为邻边做OACB,则以O为起点的向量,(OC是OACB的对角线)就是向量与的和,我们把这种作两个向量和的方法叫做向量加法的平行四边形法则
规定:对于零向量与任意向量,我们规定+=+=
平行四边形法则的适用条件:两个向量起点相同
二、向量的减法运算
定义:向量加上的相反向量,叫做与的差,即,求两个向量差
运算叫做向量的减法.
相反向量:我们规定,与向量,长度相等,方向相反的向量,叫做的相反向量,记作﹣
由于方向反转两次仍回到原来的方向,因此和﹣互为相反量,于是-(-)=.
由两个向量和的定义易知
即任意向量与其相反向量的和是零向量
几何意义:已知向量,,在平面内任取一点O,作,,则
即可以表示为从的终点指向向量的终点的向量
三、向量的数乘运算
向量数乘的定义
一般地,我们规定实数与向量的积是一个向量,这种运算叫做向量的数乘,记作,
它的长度与方向规定
如下;
当>0时,的方向与的方向相同;当<0时,的方向与的方向相反.
由可知,当=0时,=0
由可知,
四、向量数乘的运算律
根据实数与向量的积的定义,可以验证下面的运算律时成立的.
设,为实数,那么
特别的,我们有
向量的加、减数乘运算统称为向量的线性运算.向量线性运算的结果仍是向量.
对于任意向量,以任意实数,,,恒有
五、向量的数量积
向量的夹角
已知两个非零向量,,O是平面上的任意一点,作=,=,则∠AOB=叫做向量与的夹角.
显然,当时,与同向;当时,与反向.
如果与的夹角是,我们说与垂直,记作
向量数量积的定义
已知两个非零向量与,他们的夹角为,我们把数量叫做向量与的数量积,记作
即;=
规定;零向量与任一向量的数量积为0.
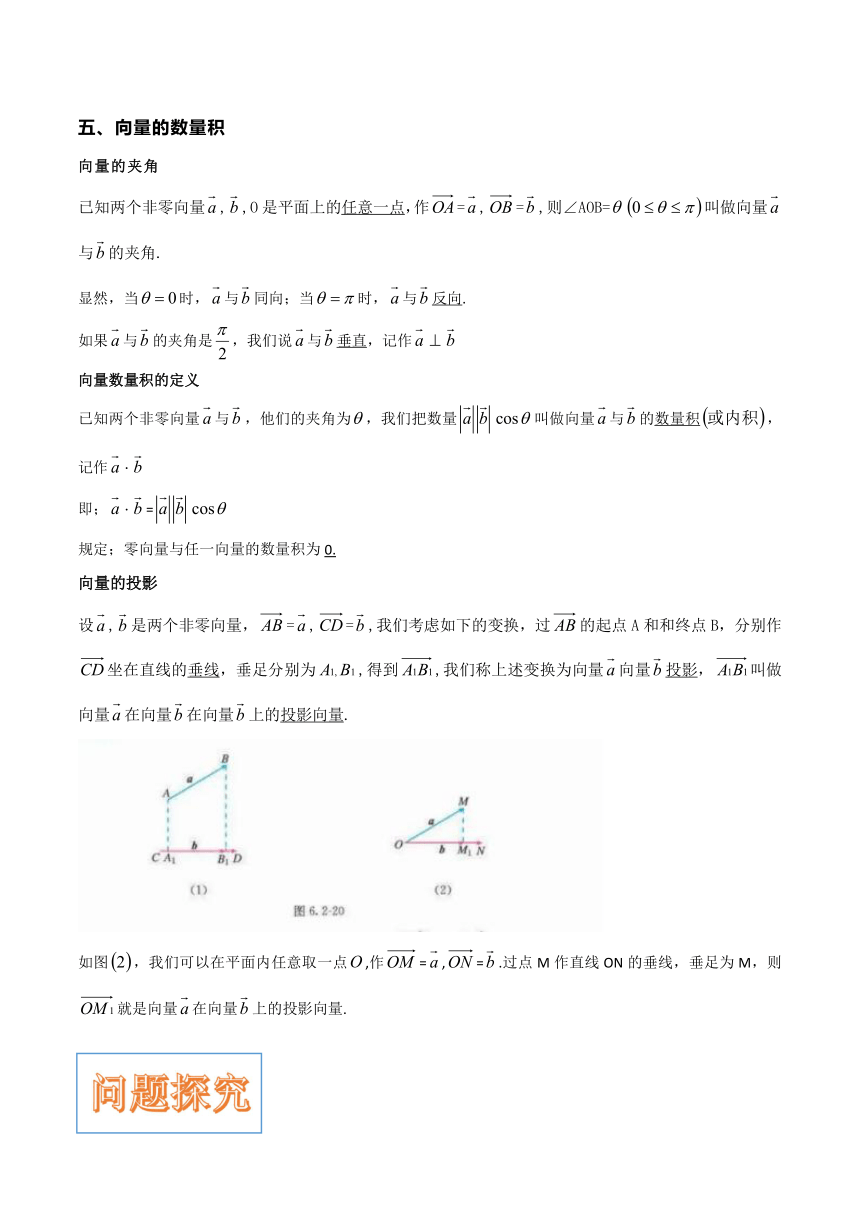
向量的投影
设,是两个非零向量,=,=,我们考虑如下的变换,过的起点A和和终点B,分别作坐在直线的垂线,垂足分别为,得到,我们称上述变换为向量向量投影,叫做向量在向量在向量上的投影向量.
如图,我们可以在平面内任意取一点,作=,=.过点M作直线ON的垂线,垂足为M,则就是向量在向量上的投影向量.
1.已知向量
,
,点
,
.
(1)求
;
(2)在直线
上,是否存在一点E,使得
,(O为原点),若存在,求出点E的坐标,若不存在,说明理由.
【答案】
(1)解:根据题意,得
,
故
.
(2)解:由于点
在直线
上,则
,
即
,
由
,则
,
所以
,解得
,
因此在直线
上存在点E,使得
,此时点E的坐标为
.
【考点】向量的共线定理,数量积的坐标表达式,平面向量数量积的运算
【解析】(1)根据向量的坐标加法运算求出
,再利用向量的模长公式即可求出
;(2)由向量共线定理和向量的线性运算得出
,从而得出
的坐标,再根据
以及向量的数量积,即可求出
的值,即可得出点
的坐标.
2.某人在静水中游泳,速度为
千米/时,现在他在水流速度为4千米/时的河中游泳.
(1)若他沿垂直于岸边的方向游向河对岸,则他实际沿什么方向前进?实际前进的速度大小为多少?
(2)他必须朝哪个方向游,才能沿与水流垂直的方向前进?实际前进的速度大小为多少?
【答案】
(1)解:如图,设此人游泳的速度为
,水流的速度为
,
以OA,OB为邻边作
QACB,则此人的实际速度为
,
由勾股定理知
,且在
中,∠COA=60°,
故此人沿与河岸成60°的夹角顺着水流的方向前进,速度大小为8千米/时
(2)解:如图,设此人的实际速度为
,水流速度为
,则游速为
,
在Rt△AOD中,
,
,则
,
,
故此人沿向量
的方向逆着水流且与河岸所成夹角的余弦值为
游,实际前进的速度大小为
千米/时
【考点】向量的三角形法则
【解析】作出示意图,再根据向量加法与减法的三角形法则和锐角三角函数的定义即可得出答案.
3.
中,点
、
、
.
(1)若D为
中点,求直线
所在直线方程;
(2)若
在线段
上,且
,求
.
【答案】
(1)解:
为
中点,
,直线
的斜率
,
所以直线
所在的直线方程为:
,即
直线方程为
(2)解:因为
,所以
,则
,
又由
,
所以
【考点】向量的模,向量的三角形法则,直线的斜截式方程
【解析】(1)求出线段
中点D的坐标,利用斜率公式求得直线
的斜率,然后利用点斜式可得出直线
所在直线的方程;(2)由
可得
,可得
,可计算出平面向量
的坐标,进而可求得
的值.
4.已知抛物线C:
=2px经过点
(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(Ⅰ)求直线l的斜率的取值范围;
(Ⅱ)设O为原点,
,
,求证:
为定值.
【答案】
解:(Ⅰ)因为抛物线y2=2px经过点P(1,2),
所以4=2p,解得p=2,所以抛物线的方程为y2=4x.
由题意可知直线l的斜率存在且不为0,
设直线l的方程为y=kx+1(k≠0).
由
得
.
依题意
,解得k<0或0又PA,PB与y轴相交,故直线l不过点(1,-2).从而k≠-3.
所以直线l斜率的取值范围是(-∞,-3)∪(-3,0)∪(0,1).
(Ⅱ)设A(x1
,
y1),B(x2
,
y2).
由(I)知
,
.
直线PA的方程为
.
令x=0,得点M的纵坐标为
.
同理得点N的纵坐标为
.
由
,
得
,
.
所以
.
所以
为定值.
【考点】向量的共线定理,直线与圆锥曲线的综合问题
【解析】
(Ⅰ)
根据题意点在抛物线上即可求出P的值由此得到抛物线的方程,由斜截式设出直线的方程再联立直线与抛物线的方程,消去y等到关于x的一元二次方程,结合题意由一元二次方程的性质限制判别式由此得到k的取值范围即可。
(Ⅱ)
由(1)的结论结合韦达定理即可得到关于k的两根之和与两根之积的代数式,进而得到直线的方程求出直线与坐标轴的交点M的坐标,同理求出N的坐标由向量共线的定理整理即可得到从而得证出结论。
1.在
中
,
,则
等于(???
)
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
2.在四边形
中,
,设
为线段
的中点,
为线段
上靠近
的三等分点,
,
,则向量
(???
)
A.??????????????????????????B.?
?C.??????????????????????????D.?
3.给出下列向量等式:①
;②
;③
其中正确的等式有(???
)
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
4.若非零向量
满足
,则(??
)
A.??????????????????B.??????????????????C.??????????????????D.?
参考答案
1.【答案】
C
【解析】
,
2.【答案】
B
【解析】
如下图所示:
在平面四边形
中,由已知条件可得
,
所以,平面四边形
为平行四边形,可得
,
为
的中点,则
,
为线段
上靠近点
的三等分点,则
,
因此,
.
3.【答案】
C
【解析】
①
,正确;
②
错误,应为
;
③
正确.
4.【答案】
B
【解析】
如图所示:
设则
,
因为
,
所以易知点A是斜边OB的中点,故是直角三角形,
则
根据直角三角形的性质,斜边大于直角边,故
,
所以选B.
【分析】由可判断是直角三角形,从而根据直角三角形的性质求解即可.
②、掌握向量线性运算的综合应用
③、理解平面向量的数量积求夹角与积求长度
一、向量的加法运算
1.定义:求两个向量和的运算,叫做向量的加法
2.向量加法的方法:向量加法的三角法则
已知非零向量,在平面内任取一点A,做=,=,则向量叫做与的和,记作,即,这种求向量和的方法,称为向量加法的三角形法则
三角形法则的使用条件:一个向量的终点为另一个向量的起点
平行四边形法则
以同一O为起点的两个已知向量,,以,为邻边做OACB,则以O为起点的向量,(OC是OACB的对角线)就是向量与的和,我们把这种作两个向量和的方法叫做向量加法的平行四边形法则
规定:对于零向量与任意向量,我们规定+=+=
平行四边形法则的适用条件:两个向量起点相同
二、向量的减法运算
定义:向量加上的相反向量,叫做与的差,即,求两个向量差
运算叫做向量的减法.
相反向量:我们规定,与向量,长度相等,方向相反的向量,叫做的相反向量,记作﹣
由于方向反转两次仍回到原来的方向,因此和﹣互为相反量,于是-(-)=.
由两个向量和的定义易知
即任意向量与其相反向量的和是零向量
几何意义:已知向量,,在平面内任取一点O,作,,则
即可以表示为从的终点指向向量的终点的向量
三、向量的数乘运算
向量数乘的定义
一般地,我们规定实数与向量的积是一个向量,这种运算叫做向量的数乘,记作,
它的长度与方向规定
如下;
当>0时,的方向与的方向相同;当<0时,的方向与的方向相反.
由可知,当=0时,=0
由可知,
四、向量数乘的运算律
根据实数与向量的积的定义,可以验证下面的运算律时成立的.
设,为实数,那么
特别的,我们有
向量的加、减数乘运算统称为向量的线性运算.向量线性运算的结果仍是向量.
对于任意向量,以任意实数,,,恒有
五、向量的数量积
向量的夹角
已知两个非零向量,,O是平面上的任意一点,作=,=,则∠AOB=叫做向量与的夹角.
显然,当时,与同向;当时,与反向.
如果与的夹角是,我们说与垂直,记作
向量数量积的定义
已知两个非零向量与,他们的夹角为,我们把数量叫做向量与的数量积,记作
即;=
规定;零向量与任一向量的数量积为0.
向量的投影
设,是两个非零向量,=,=,我们考虑如下的变换,过的起点A和和终点B,分别作坐在直线的垂线,垂足分别为,得到,我们称上述变换为向量向量投影,叫做向量在向量在向量上的投影向量.
如图,我们可以在平面内任意取一点,作=,=.过点M作直线ON的垂线,垂足为M,则就是向量在向量上的投影向量.
1.已知向量
,
,点
,
.
(1)求
;
(2)在直线
上,是否存在一点E,使得
,(O为原点),若存在,求出点E的坐标,若不存在,说明理由.
【答案】
(1)解:根据题意,得
,
故
.
(2)解:由于点
在直线
上,则
,
即
,
由
,则
,
所以
,解得
,
因此在直线
上存在点E,使得
,此时点E的坐标为
.
【考点】向量的共线定理,数量积的坐标表达式,平面向量数量积的运算
【解析】(1)根据向量的坐标加法运算求出
,再利用向量的模长公式即可求出
;(2)由向量共线定理和向量的线性运算得出
,从而得出
的坐标,再根据
以及向量的数量积,即可求出
的值,即可得出点
的坐标.
2.某人在静水中游泳,速度为
千米/时,现在他在水流速度为4千米/时的河中游泳.
(1)若他沿垂直于岸边的方向游向河对岸,则他实际沿什么方向前进?实际前进的速度大小为多少?
(2)他必须朝哪个方向游,才能沿与水流垂直的方向前进?实际前进的速度大小为多少?
【答案】
(1)解:如图,设此人游泳的速度为
,水流的速度为
,
以OA,OB为邻边作
QACB,则此人的实际速度为
,
由勾股定理知
,且在
中,∠COA=60°,
故此人沿与河岸成60°的夹角顺着水流的方向前进,速度大小为8千米/时
(2)解:如图,设此人的实际速度为
,水流速度为
,则游速为
,
在Rt△AOD中,
,
,则
,
,
故此人沿向量
的方向逆着水流且与河岸所成夹角的余弦值为
游,实际前进的速度大小为
千米/时
【考点】向量的三角形法则
【解析】作出示意图,再根据向量加法与减法的三角形法则和锐角三角函数的定义即可得出答案.
3.
中,点
、
、
.
(1)若D为
中点,求直线
所在直线方程;
(2)若
在线段
上,且
,求
.
【答案】
(1)解:
为
中点,
,直线
的斜率
,
所以直线
所在的直线方程为:
,即
直线方程为
(2)解:因为
,所以
,则
,
又由
,
所以
【考点】向量的模,向量的三角形法则,直线的斜截式方程
【解析】(1)求出线段
中点D的坐标,利用斜率公式求得直线
的斜率,然后利用点斜式可得出直线
所在直线的方程;(2)由
可得
,可得
,可计算出平面向量
的坐标,进而可求得
的值.
4.已知抛物线C:
=2px经过点
(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(Ⅰ)求直线l的斜率的取值范围;
(Ⅱ)设O为原点,
,
,求证:
为定值.
【答案】
解:(Ⅰ)因为抛物线y2=2px经过点P(1,2),
所以4=2p,解得p=2,所以抛物线的方程为y2=4x.
由题意可知直线l的斜率存在且不为0,
设直线l的方程为y=kx+1(k≠0).
由
得
.
依题意
,解得k<0或0
所以直线l斜率的取值范围是(-∞,-3)∪(-3,0)∪(0,1).
(Ⅱ)设A(x1
,
y1),B(x2
,
y2).
由(I)知
,
.
直线PA的方程为
.
令x=0,得点M的纵坐标为
.
同理得点N的纵坐标为
.
由
,
得
,
.
所以
.
所以
为定值.
【考点】向量的共线定理,直线与圆锥曲线的综合问题
【解析】
(Ⅰ)
根据题意点在抛物线上即可求出P的值由此得到抛物线的方程,由斜截式设出直线的方程再联立直线与抛物线的方程,消去y等到关于x的一元二次方程,结合题意由一元二次方程的性质限制判别式由此得到k的取值范围即可。
(Ⅱ)
由(1)的结论结合韦达定理即可得到关于k的两根之和与两根之积的代数式,进而得到直线的方程求出直线与坐标轴的交点M的坐标,同理求出N的坐标由向量共线的定理整理即可得到从而得证出结论。
1.在
中
,
,则
等于(???
)
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
2.在四边形
中,
,设
为线段
的中点,
为线段
上靠近
的三等分点,
,
,则向量
(???
)
A.??????????????????????????B.?
?C.??????????????????????????D.?
3.给出下列向量等式:①
;②
;③
其中正确的等式有(???
)
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
4.若非零向量
满足
,则(??
)
A.??????????????????B.??????????????????C.??????????????????D.?
参考答案
1.【答案】
C
【解析】
,
2.【答案】
B
【解析】
如下图所示:
在平面四边形
中,由已知条件可得
,
所以,平面四边形
为平行四边形,可得
,
为
的中点,则
,
为线段
上靠近点
的三等分点,则
,
因此,
.
3.【答案】
C
【解析】
①
,正确;
②
错误,应为
;
③
正确.
4.【答案】
B
【解析】
如图所示:
设则
,
因为
,
所以易知点A是斜边OB的中点,故是直角三角形,
则
根据直角三角形的性质,斜边大于直角边,故
,
所以选B.
【分析】由可判断是直角三角形,从而根据直角三角形的性质求解即可.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
