8.2立体图形的直观图-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册学案Word
文档属性
| 名称 | 8.2立体图形的直观图-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册学案Word |  | |
| 格式 | docx | ||
| 文件大小 | 158.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-19 19:07:48 | ||
图片预览


文档简介
1、会用斜二测画法画水平放置的平面图形的直观图
2、会用斜二测画法画常见的柱、锥、台以及简单组合体的直观图
3、会根据斜二测画法规则进行相关运算
1、直观图
定义:直观图是观察者站在某一点观察一个空间几何图获得的图形,画立体图形的直观图,实际上是把不完全在同一平面内的点的集合,用同一平面内的点表示。
因此,直观图汪汪与立体图形的真实形状不完全相同。
在立体几何中,立体图形的直观图通常是在平行投影下得到的平面图形
画法:斜二测画法和正等测画法.
2、斜二测画法规则
(1)在己知图形中取互相重直的x轴或y轴,两轴相交于点O,画直观图时,把它们画成对应的x,轴与y'轴,两轴相交于点O,,且=45°(或135°),它们确定的平面表示水平面
(2)已知图形中平行于x轴或y轴的线段。在直观图中分剔画成平行于x,轴与y,轴的线段
(3)已知图形中平行于x轴的线段,在直观图中保持原长度不变,平行于y轴的线段,在直观图中长度为原来的一半
给出斜二测具体步骤
(1)在已知图形中取互相垂直的X轴Y轴,两轴相交于O,画直观图时,把他们画成对应的X'轴与Y'轴,两轴交于O'。且使∠X'O'Y'=45°(或135°)。他们确定的平面表示水平面。
(2)已知图形中平行于X轴或y轴的线段,在直观图中分别画成平行于X'轴或y'轴的线段。
(3)已知图形中平行于X轴的线段,在直观图中保持原长度不变,平行于Y轴的线段,在直观图中长度为原来一半。
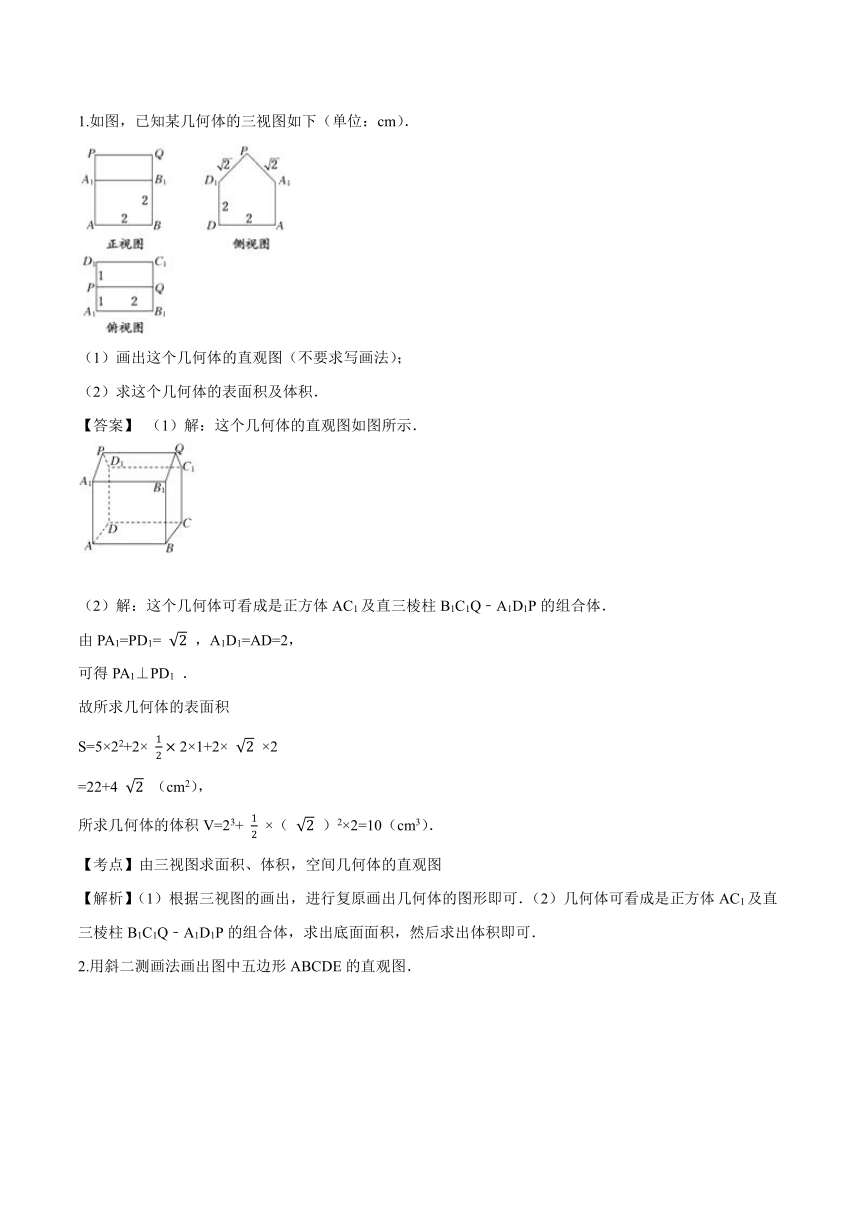
1.如图,已知某几何体的三视图如下(单位:cm).
(1)画出这个几何体的直观图(不要求写画法);
(2)求这个几何体的表面积及体积.
【答案】
(1)解:这个几何体的直观图如图所示.
(2)解:这个几何体可看成是正方体AC1及直三棱柱B1C1Q﹣A1D1P的组合体.
由PA1=PD1=
,A1D1=AD=2,
可得PA1⊥PD1
.
故所求几何体的表面积
S=5×22+2×
2×1+2×
×2
=22+4
(cm2),
所求几何体的体积V=23+
×(
)2×2=10(cm3).
【考点】由三视图求面积、体积,空间几何体的直观图
【解析】(1)根据三视图的画出,进行复原画出几何体的图形即可.(2)几何体可看成是正方体AC1及直三棱柱B1C1Q﹣A1D1P的组合体,求出底面面积,然后求出体积即可.
2.用斜二测画法画出图中五边形ABCDE的直观图.
【答案】
【解答】解:在原图形中作BF⊥x轴,EG⊥x轴,垂足分别为F、G,
1、作坐标系x′O′y′,使∠x′O′y′=45°,
2、在x′轴上取点C′,D′,F′,G′使O′C′=OC,O′D′=OD,O′F′=OF,O′G′=OG;
3、在y′轴上取点A′,使O′A′=OA,作F′B′∥y′,使F′B′=FB,作G′E′∥y′,使G′E′=GE;
4、连接A′B′,B′C′,D′E′,E′A′,得五边形ABCDE的直观图.
(正五边形的直观图的形状如下图所示)
【考点】斜二测法画直观图
【解析】在原图形中建立平面直角坐标系,作BF⊥x轴于F,EG⊥y轴于G,利用斜二测画法画出直观图.
3.如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面与此长方体的面相交,交线围成一个正方形。
(1)(I)在图中画出这个正方形(不必说明画法与理由);
(2)(II)求平面
把该长方体分成的两部分体积的比值.
【答案】
(1)交线围成的正方形EHGF
如图:
(2)或
【考点】组合几何体的面积、体积问题,空间几何体的直观图
【解析】【解答】
(II)作EMAB,垂足为M,则AM=A1E=4,EB1=12,EM=AA1=8,因为EHGF是正方形,所以EH=EF=BC=10,于是MH=
,
AH=10,HB=6,因为长方体被平面分成两个高为10的直棱柱,所以其体积比值为(也正确)。
【分析】立体几何解答题在高考中难度低于解析几何,属于得分题,往年第一问多为线位置关系得证明,今年试题有所创新,改为作截面图,令人耳目一新。第二问求两几何体体积之比,方法容易想到,注意运算不要出现错误
4.如图是某几何体的三视图.试说明该几何体的结构特征,并用斜二测画法画出它的直观图.
【答案】
解:根据几何体的三视图,得,
该几何体是上部为正六棱柱,下部为正六棱锥的组合体;
画出该几何体的直观图,如图所示;
【考点】空间几何体的直观图
【解析】根据几何体的三视图,得出该几何体是上部为正六棱柱,下部为正六棱锥的组合体;
画出它的直观图即可.
1.攒尖是古代中国建筑中屋顶的一种结构形式.宋代称为撮尖,清代称攒尖通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖.也有单檐和重檐之分.多见于亭阁式建筑,园林建筑以四角攒尖为例,它的主要部分的轮廓可近似看作一个正四棱锥.若此正四棱锥的侧面等腰三角形的底角为
,则侧棱长与底面外接圆的半径的比为(???
)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
2设
、
、…、
为平面
内的
个点,在平面
内的所有点中,若点
到
、
、…、
点的距离之和最小,则称点
为
、
、…、
点的一个“中位点”,有下列命题:①
、
、
三个点共线,
在线段
上,则
是
、
、
的中位点;②直角三角形斜边的中点是该直线三角形三个顶点的中位点;③若四个点
、
、
、
共线,则它们的中位点存在且唯一;④梯形对角线的交点是该梯形四个顶点的唯一中位点;其中的真命题是(?????????
)
A.?②④????????????????????????????????????B.?①②????????????????????????????????????C.?①④????????????????????????????????????D.?①③④
3.已知梯形
是直角梯形,
,
,且
,
,
.按照斜二测画法作出它的直观图
,则直观图
面积为(??
)
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
4.如图,已知
的直观图
是一个直角边长是1的等腰直角三角形,那么
的面积是(????
)
??????????????????????????????????????????B.??????????????????????????????????????????C.?1?????????????????????????????????????????D.?
参考答案
1.【答案】
D
【解析】
正四棱锥的底面为正方形,设其外接圆半径为
,则底面正边形的边长为
,
因为正四棱锥的侧面等腰三角形的底角为
,
设侧棱长为
,则有
,
解得
,
所以侧棱与底面外接圆半径的比为
.
2.【答案】
C
【解析】
①若三个点
共线,
在线段
上,根据两点之间线段最短,
则
是
的中位点,正确;②举一个反例,如边长为
的直角三角形
,此直角三角形的斜边的中点到三个顶点的距离之和为
,而直角顶点到三个顶点的距离之和为7,
∴直角三角形斜边的中点不是该直角三角形三个顶点的中位点;故错误;③若四个点
共线,则它们的中位点是中间两点连线段上的任意一个点,故它们的中位点存在但不唯一;故错误;④如图,在梯形
中,对角线的交点
是任意一点,则根据三角形两边之和大于第三边得
,
∴梯形对角线的交点是该梯形四个顶点的唯一中位点.正确.
故①④正确.
3.【答案】
D
【解析】
梯形
的面积为
,则直观图
的面积为
.
4.【答案】
D
【解析】
平面直观图
与其原图形如图,
直观图
是直角边长为
的等腰直角三角形,
还原回原图形后,边
还原为
长度不变,仍为
,
直观图中的
在原图形中还原为
长度,且长度为
,
所以原图形的面积为
,
2、会用斜二测画法画常见的柱、锥、台以及简单组合体的直观图
3、会根据斜二测画法规则进行相关运算
1、直观图
定义:直观图是观察者站在某一点观察一个空间几何图获得的图形,画立体图形的直观图,实际上是把不完全在同一平面内的点的集合,用同一平面内的点表示。
因此,直观图汪汪与立体图形的真实形状不完全相同。
在立体几何中,立体图形的直观图通常是在平行投影下得到的平面图形
画法:斜二测画法和正等测画法.
2、斜二测画法规则
(1)在己知图形中取互相重直的x轴或y轴,两轴相交于点O,画直观图时,把它们画成对应的x,轴与y'轴,两轴相交于点O,,且=45°(或135°),它们确定的平面表示水平面
(2)已知图形中平行于x轴或y轴的线段。在直观图中分剔画成平行于x,轴与y,轴的线段
(3)已知图形中平行于x轴的线段,在直观图中保持原长度不变,平行于y轴的线段,在直观图中长度为原来的一半
给出斜二测具体步骤
(1)在已知图形中取互相垂直的X轴Y轴,两轴相交于O,画直观图时,把他们画成对应的X'轴与Y'轴,两轴交于O'。且使∠X'O'Y'=45°(或135°)。他们确定的平面表示水平面。
(2)已知图形中平行于X轴或y轴的线段,在直观图中分别画成平行于X'轴或y'轴的线段。
(3)已知图形中平行于X轴的线段,在直观图中保持原长度不变,平行于Y轴的线段,在直观图中长度为原来一半。
1.如图,已知某几何体的三视图如下(单位:cm).
(1)画出这个几何体的直观图(不要求写画法);
(2)求这个几何体的表面积及体积.
【答案】
(1)解:这个几何体的直观图如图所示.
(2)解:这个几何体可看成是正方体AC1及直三棱柱B1C1Q﹣A1D1P的组合体.
由PA1=PD1=
,A1D1=AD=2,
可得PA1⊥PD1
.
故所求几何体的表面积
S=5×22+2×
2×1+2×
×2
=22+4
(cm2),
所求几何体的体积V=23+
×(
)2×2=10(cm3).
【考点】由三视图求面积、体积,空间几何体的直观图
【解析】(1)根据三视图的画出,进行复原画出几何体的图形即可.(2)几何体可看成是正方体AC1及直三棱柱B1C1Q﹣A1D1P的组合体,求出底面面积,然后求出体积即可.
2.用斜二测画法画出图中五边形ABCDE的直观图.
【答案】
【解答】解:在原图形中作BF⊥x轴,EG⊥x轴,垂足分别为F、G,
1、作坐标系x′O′y′,使∠x′O′y′=45°,
2、在x′轴上取点C′,D′,F′,G′使O′C′=OC,O′D′=OD,O′F′=OF,O′G′=OG;
3、在y′轴上取点A′,使O′A′=OA,作F′B′∥y′,使F′B′=FB,作G′E′∥y′,使G′E′=GE;
4、连接A′B′,B′C′,D′E′,E′A′,得五边形ABCDE的直观图.
(正五边形的直观图的形状如下图所示)
【考点】斜二测法画直观图
【解析】在原图形中建立平面直角坐标系,作BF⊥x轴于F,EG⊥y轴于G,利用斜二测画法画出直观图.
3.如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面与此长方体的面相交,交线围成一个正方形。
(1)(I)在图中画出这个正方形(不必说明画法与理由);
(2)(II)求平面
把该长方体分成的两部分体积的比值.
【答案】
(1)交线围成的正方形EHGF
如图:
(2)或
【考点】组合几何体的面积、体积问题,空间几何体的直观图
【解析】【解答】
(II)作EMAB,垂足为M,则AM=A1E=4,EB1=12,EM=AA1=8,因为EHGF是正方形,所以EH=EF=BC=10,于是MH=
,
AH=10,HB=6,因为长方体被平面分成两个高为10的直棱柱,所以其体积比值为(也正确)。
【分析】立体几何解答题在高考中难度低于解析几何,属于得分题,往年第一问多为线位置关系得证明,今年试题有所创新,改为作截面图,令人耳目一新。第二问求两几何体体积之比,方法容易想到,注意运算不要出现错误
4.如图是某几何体的三视图.试说明该几何体的结构特征,并用斜二测画法画出它的直观图.
【答案】
解:根据几何体的三视图,得,
该几何体是上部为正六棱柱,下部为正六棱锥的组合体;
画出该几何体的直观图,如图所示;
【考点】空间几何体的直观图
【解析】根据几何体的三视图,得出该几何体是上部为正六棱柱,下部为正六棱锥的组合体;
画出它的直观图即可.
1.攒尖是古代中国建筑中屋顶的一种结构形式.宋代称为撮尖,清代称攒尖通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖.也有单檐和重檐之分.多见于亭阁式建筑,园林建筑以四角攒尖为例,它的主要部分的轮廓可近似看作一个正四棱锥.若此正四棱锥的侧面等腰三角形的底角为
,则侧棱长与底面外接圆的半径的比为(???
)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
2设
、
、…、
为平面
内的
个点,在平面
内的所有点中,若点
到
、
、…、
点的距离之和最小,则称点
为
、
、…、
点的一个“中位点”,有下列命题:①
、
、
三个点共线,
在线段
上,则
是
、
、
的中位点;②直角三角形斜边的中点是该直线三角形三个顶点的中位点;③若四个点
、
、
、
共线,则它们的中位点存在且唯一;④梯形对角线的交点是该梯形四个顶点的唯一中位点;其中的真命题是(?????????
)
A.?②④????????????????????????????????????B.?①②????????????????????????????????????C.?①④????????????????????????????????????D.?①③④
3.已知梯形
是直角梯形,
,
,且
,
,
.按照斜二测画法作出它的直观图
,则直观图
面积为(??
)
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
4.如图,已知
的直观图
是一个直角边长是1的等腰直角三角形,那么
的面积是(????
)
??????????????????????????????????????????B.??????????????????????????????????????????C.?1?????????????????????????????????????????D.?
参考答案
1.【答案】
D
【解析】
正四棱锥的底面为正方形,设其外接圆半径为
,则底面正边形的边长为
,
因为正四棱锥的侧面等腰三角形的底角为
,
设侧棱长为
,则有
,
解得
,
所以侧棱与底面外接圆半径的比为
.
2.【答案】
C
【解析】
①若三个点
共线,
在线段
上,根据两点之间线段最短,
则
是
的中位点,正确;②举一个反例,如边长为
的直角三角形
,此直角三角形的斜边的中点到三个顶点的距离之和为
,而直角顶点到三个顶点的距离之和为7,
∴直角三角形斜边的中点不是该直角三角形三个顶点的中位点;故错误;③若四个点
共线,则它们的中位点是中间两点连线段上的任意一个点,故它们的中位点存在但不唯一;故错误;④如图,在梯形
中,对角线的交点
是任意一点,则根据三角形两边之和大于第三边得
,
∴梯形对角线的交点是该梯形四个顶点的唯一中位点.正确.
故①④正确.
3.【答案】
D
【解析】
梯形
的面积为
,则直观图
的面积为
.
4.【答案】
D
【解析】
平面直观图
与其原图形如图,
直观图
是直角边长为
的等腰直角三角形,
还原回原图形后,边
还原为
长度不变,仍为
,
直观图中的
在原图形中还原为
长度,且长度为
,
所以原图形的面积为
,
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
