9.3统计案例 公司员工的肥胖情况调查分析-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册学案
文档属性
| 名称 | 9.3统计案例 公司员工的肥胖情况调查分析-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册学案 |  | |
| 格式 | docx | ||
| 文件大小 | 63.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-19 19:10:16 | ||
图片预览




文档简介
①、了解平均数、中位数、和众数的应用
②、掌握统计的实际应用
③、理解频率分布表与频率分布图
一、统计案例
公司员工的肥胖情况调查分析
背景与数据
近年来,我国肥胖人群的规模急速增长,肥胖人群有很大的心血管安全隐患.目前,国际上常用身体质量指数来衡量人体胖瘦程度以及是否健康,其计算公式是
BMI=
中国成人的BMI数值标准为:BM1<18.5为偏瘦;18.5≤BMI<23.9为正常;24≤?BMI<27.9为偏胖;BMI≥28为肥胖.
二、对方差、标准差的理解
(1)标准差、方差描述了一组数据围绕平均数波动的大小.标准差、方差越大,数据的离散程度越大;标准差、方差越小,数据的离散程度越小.
(2)标准差、方差的取值范围:[0,+∞).
标准差、方差为0时,样本各数据全相等,表明数据没有波动幅度,数据没有离散性.
标准差的意义
标准差刻画了数据的离散程度或波动幅度,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小.
1.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到如下列联表(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
常喝
不常喝
合计
肥胖
2
不肥胖
18
合计
30
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)现从常喝碳酸饮料且肥胖的学生中(2名女生),抽取2人参加电视节目,则正好抽到一男一女的概率是多少
P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
K
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:K2=
,其中n=a+b+c+d)
【答案】
(1)解:设常喝碳酸饮料肥胖的学生有x人,
.
常喝
不常喝
合计
肥胖
6
2
8
?不胖
4
18
22
合计
10
20
30
(2)解:由已知数据可求得:
因此有99.5%的把握认为肥胖与常喝碳酸饮料有关
(3)解:设常喝碳酸饮料的肥胖者男生为A、B、C、D,女生为E、F,则任取两人有
AB,AC,AD,AE,AF,BC,BD,BE,BF,CD,CE,CF,DE,DF,EF,共15种.
其中一男一女有AE,AF,BE,BF,CE,CF,DE,DF.共8种.
故抽出一男一女的概率是
【考点】独立性检验的应用,列举法计算基本事件数及事件发生的概率
【解析】(1)设常喝碳酸饮料肥胖的学生有x人,
.即可将上面的列联表补充完整;(2)根据列联表所给的数据,代入求观测值的公式,把观测值同临界值进行比较,得到有99.5%的把握说看营养说明与性别有关.(3)利用列举法,求出基本事件的个数,即可求出正好抽到一男一女的概率.
2.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名五年级学生进行了问卷调查,得到如下2×2列联表,平均每天喝500
以上为常喝,体重超过50
为肥胖.
?
不常喝
常喝
合计
肥胖
50
不肥胖
40
10
50
合计
A
B
100
现从这100名儿童中随机抽取1人,抽到不常喝碳酸饮料的学生的概率为
.
附:参考公式:
,其中
.
临界值表:
P(
)
0.05
0.025
0.010
0.005
0.001
3.841
5.024
6.635
7.879
10.828
(1)求2×2列联表中的数据
,
,A,B的值;
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
【答案】
(1)解:根据题意,不常喝碳酸饮料的学生为
,
∴
,
,
;
(2)解:有99.5%的把握认为肥胖与常喝碳酸饮料有关,理由如下:
由已知数据可求得:
,
因此有99.5%的把握认为肥胖与常喝碳酸饮料有关.
【考点】独立性检验的应用
【解析】(1)利用实际问题中的已知条件求出并填写出2×2列联表中的数据
,
,A,B的值。
(2)利用(1)中的2×2列联表结合独立性检验的方法,从而判断出有99.5%的把握认为肥胖与常喝碳酸饮料有关。
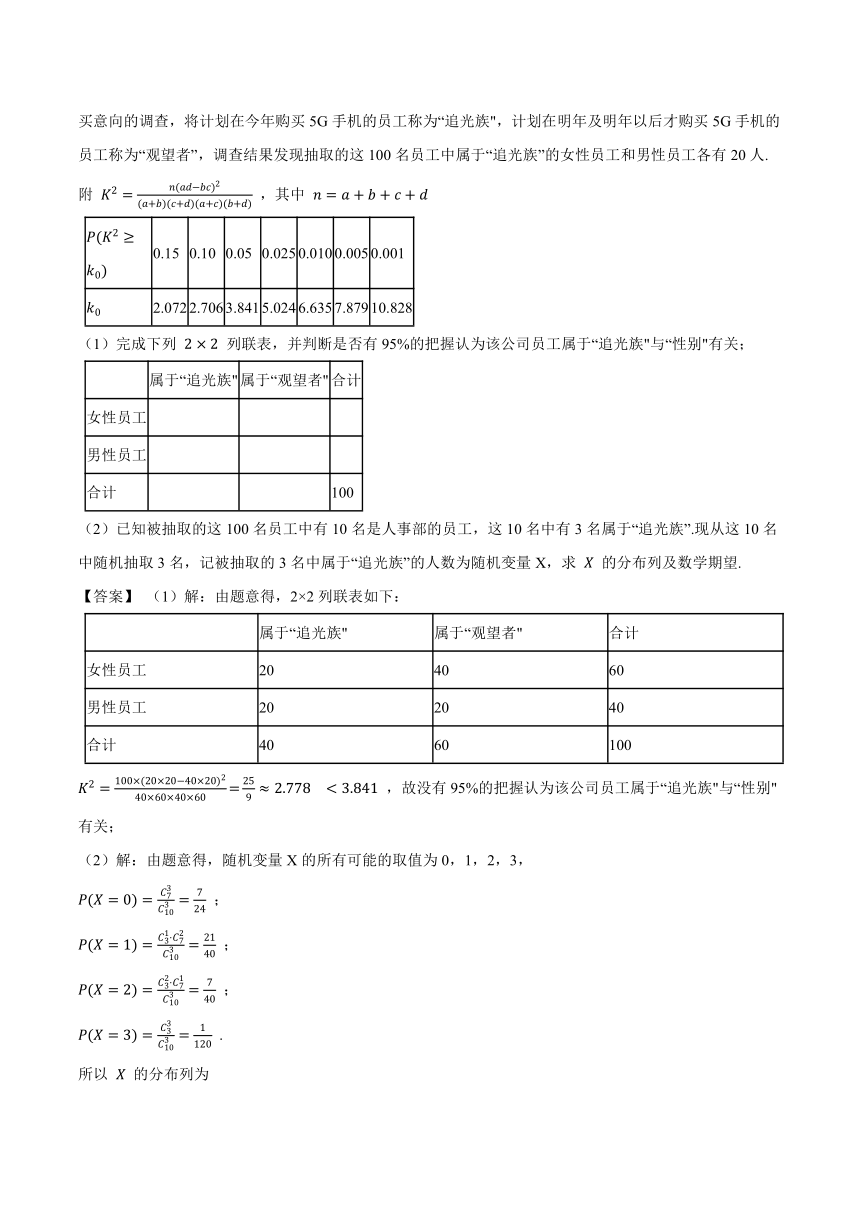
3.某公司有1000名员工,其中男性员工400名,采用分层抽样的方法随机抽取100名员工进行5G手机购买意向的调查,将计划在今年购买5G手机的员工称为“追光族",计划在明年及明年以后才购买5G手机的员工称为“观望者”,调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人.
附
,其中
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)完成下列
列联表,并判断是否有95%的把握认为该公司员工属于“追光族"与“性别"有关;
属于“追光族"
属于“观望者"
合计
女性员工
男性员工
合计
100
(2)已知被抽取的这100名员工中有10名是人事部的员工,这10名中有3名属于“追光族”.现从这10名中随机抽取3名,记被抽取的3名中属于“追光族”的人数为随机变量X,求
的分布列及数学期望.
【答案】
(1)解:由题意得,2×2列联表如下:
属于“追光族"
属于“观望者"
合计
女性员工
20
40
60
男性员工
20
20
40
合计
40
60
100
,故没有95%的把握认为该公司员工属于“追光族"与“性别"有关;
(2)解:由题意得,随机变量X的所有可能的取值为0,1,2,3,
;
;
;
.
所以
的分布列为
X
0
1
2
3
P
【考点】独立性检验,离散型随机变量及其分布列,离散型随机变量的期望与方差
【解析】(1)根据题意,列出列联表,计算K2
,
查表判断即可;(2)随机变量X的所有可能取值为0,1,2,3,分布求出对应概率,列出分布列,求期望即可.
4.近年来,我国肥胖人群的规模急速增长,肥胖人群有着很大的健康隐患.目前,国际上常用身体质量指数(英文为
,简称
)来衡量人体胖瘦程度以及是否健康,其计算公式是
中国成人的
数值标准为:
为偏瘦;
为正常;
为偏胖;
为肥胖.某地区随机调查了6000名35岁以上成人的身体健康状况,其中有1000名高血压患者,得到被调查者的频率分布直方图如图:
参考公式:
,其中
.
参考数据:
0.25
0.10
0.050
0.010
0.001
1.323
2.706
3.841
6.635
10.828
(1)求被调查者中肥胖人群的
平均值
;
(2)根据频率分布直方图,完成下面的2×2列联表,并判断能有多大(百分数)的把握认为35岁以上成人高血压与肥胖有关?
肥胖
不肥胖
总计
高血压
非高血压
总计
【答案】
(1)解:由图可知,1000名高血压患者中:
,
,
,
人数
5000名非高血压患者中:
,
,
,
人数
被调查者中肥胖人群的
平均值
.
(2)解:由(1)及频率分布直方图知,1000名高血压患者中有
人肥胖,5000名非高血压患者中有
人肥胖,所以可得下列列表:
肥胖
不肥胖
总计
高血压
350
650
1000
非高血压
1150
3850
5000
总计
1500
4500
6000
由列联表中数据得
的观测值为
,
所以能有
的把握认为35岁以上成人高血压与肥胖有关.
【考点】频率分布直方图,独立性检验
【解析】(1)利用频率分布直方图,填写分布表,利用频率分布直方图求解被调查者中肥胖人群的
平均值;
(2)求出
,
对照参考数据,判断有多大
(百分数)
的把握认为35岁以上成人高血压与肥胖有关。
5.某公司有1400名员工,其中男员工900名,用分层抽样的方法随机抽取28名员工进行5G手机购买意向调查,将计划在今年购买5G手机的员工称为“追光族”,计划在明年及明年以后购买5G手机的员工称为“观望者”,调查结果发现抽取的这28名员工中属于“追光族”的女员工有2人,男员工有10人.
附:
,其中
.
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)完成下面2×2列联表,并判断是否有95%的把握认为该公司员工属于“追光族”与“性别”有关;
属于“追光族”
属于“观望者”
合计
女员工
男员工
合计
28
(2)在抽取的属于“追光族”的员工中任选4人,记选出的4人中男员工有
人,女员工有
人,求随机变量
的分布列与数学期望.
【答案】
(1)解:由题意得:2×2列联表如下:
属于“追光族"
属于“观望者"
合计
女员工
2
8
10
男员工
10
8
18
合计
12
16
28
,
故没有95%的把握认为该公司员工属于“追光族”与“性别”有关;
(2)解:由(1)知在样本里属于“追光族"的员工有12人.其中男员工10人,女员工2人,
所以
可能的取值有
,
,
,
,
的分布列为:
0
2
4
的期望
.
【考点】独立性检验的应用,离散型随机变量及其分布列
【解析】(1)利用实际问题的已知条件填写
2×2列联表,
再利用
2×2列联表结合独立性检验的方法,判断出没有95%的把握认为该公司员工属于“追光族”与“性别”有关。
(2)利用分层抽样的方法推出属于“追光族"的员工有12人,其中男员工10人,女员工2人,
所以
可能的取值有
,
进而利用组合数公式结合古典概型求概率的方法,从而求出随机变量
的分别列,再利用随机变量
的分布列结合数学期望公式,进而求出随机变量
的数学期望
。
6.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对
名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝
以上为“常喝”,体重超过
为“肥胖”.
常喝
不常喝
合计
肥胖
2
不肥胖
18
合计
30
已知在全部
人中随机抽取
人,抽到肥胖的学生的概率为
.
附:
?
p(k2>k)
0.15
0.10
0.05
0.25
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)请将上面的列联表补充完整;
(2)是否有
的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
(3)已知常喝碳酸饮料且肥胖的学生中恰有2名女生,现从常喝碳酸饮料且肥胖的学生中随机抽取2人参加一个有关健康饮食的电视节目,求恰好抽到一名男生和一名女生的概率.
【答案】
(1)解:设全部30人中的肥胖学生共
名,则
,解得
.∴常喝碳酸饮料且肥胖的学生有6名.列联表如下:
常喝
不常喝
合计
肥胖
6
2
8
不肥胖
4
18
22
合计
10
20
30
(2)解:有;
理由:由已知数据可求得
,因此有99.5%的把握认为肥胖与常喝碳酸饮料有关.
(3)解:根据题意,可设常喝碳酸饮料的肥胖男生为
,女生为
,则任取两人,
可能的结果有
?共15种,其中一男一女有
,
共8种.故正好抽到一男一女的概率为
【考点】独立性检验,相关系数,列举法计算基本事件数及事件发生的概率
【解析】(1)由已知数据,即可将列联表补充完整;
(2)
由已知数据可得
,即可判断相关关系;
(3)由已知利用列举法,分别得
随机抽取2人和恰好抽到一名男生和一名女生的种数,即可求出概率.
7.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名五年级学生进行了问卷调查,得到如下2×2列联表,平均每天喝500ml以上为常喝,体重超过50kg为肥胖.
不常喝
常喝
合计
肥胖
x
y
50
不肥胖
40
10
50
合计
A
B
100
现从这100名儿童中随机抽取1人,抽到不常喝碳酸饮料的学生的概率为
(1)求2×2列联表中的数据x,y,A,B的值;
(2)根据列联表中的数据绘制肥胖率的条形统计图,并判断常喝碳酸饮料是否影响肥胖?
(3)是否有99.9%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
附:参考公式:K2=
,其中n=a+b+c+d.
临界值表:
P(K2≥k)
0.05
0.025
0.010
0.005
0.001
k
3.841
5.024
6.635
7.879
10.828
【答案】
(1)解:根据题意,不常喝碳酸饮料的学生为A=100×
=60,∴x=60﹣40=20,y=50﹣20=30,B=30+10=40
(2)解:根据列联表中的数据得常喝饮料的肥胖率为
=0.75,
不常喝饮料的肥胖率为
=0.33,
绘制肥胖率的条形统计图如图所示;
根据统计图判断常喝碳酸饮料会增加肥胖的可能
(3)解:由已知数据可求得:K2=
≈15.629>7.879,
因此有99.5%的把握认为肥胖与常喝碳酸饮料有关.
【考点】独立性检验
【解析】(1)根据题意,计算不常喝碳酸饮料的学生A,以及对应表中x、y和B的值;(2)根据列联表中的数据计算常喝饮料与不常喝饮料的肥胖率,绘图即可;根据统计图即可得出概率结论;(3)计算观测值K2
,
对照数表即可得出结论.
8.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名六年级学生进行了问卷调查得到如图联表.且平均每天喝500ml以上为常喝,体重超过50kg为肥胖.已知在全部100人中随机抽取1人,抽到肥胖的学生的概率为0.8.
常喝
不常喝
合计
肥胖
60
不肥胖
10
合计
100
(1)求肥胖学生的人数并将上面的列联表补充完整;
(2)是否有95%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
附:参考公式:x2=
P(x2≥x0)
0.05
0.025
0.010
0.005
0.001
x0
3.841
5.024
6.635
7.879
10.828
【答案】
(1)解:在全部100人中随机抽取1人,抽到肥胖的学生的概率为0.8,则肥胖的学生为80人;
常喝
不常喝
合计
肥胖
60
20
80
不胖
10
10
20
合计
70
30
100
(2)解:由已知数据可求得:K2=
≈4.76>3.841,
因此有95%的把握认为肥胖与常喝碳酸饮料有关
【考点】独立性检验的应用
【解析】(1)根据在全部100人中随机抽取1人,抽到肥胖的学生的概率为0.8,做出肥胖的学生人数,即可填上所有数字.(2)根据列联表所给的数据,代入求观测值的公式,把观测值同临界值进行比较,得到有95%的把握说看营养说明与性别有关.
②、掌握统计的实际应用
③、理解频率分布表与频率分布图
一、统计案例
公司员工的肥胖情况调查分析
背景与数据
近年来,我国肥胖人群的规模急速增长,肥胖人群有很大的心血管安全隐患.目前,国际上常用身体质量指数来衡量人体胖瘦程度以及是否健康,其计算公式是
BMI=
中国成人的BMI数值标准为:BM1<18.5为偏瘦;18.5≤BMI<23.9为正常;24≤?BMI<27.9为偏胖;BMI≥28为肥胖.
二、对方差、标准差的理解
(1)标准差、方差描述了一组数据围绕平均数波动的大小.标准差、方差越大,数据的离散程度越大;标准差、方差越小,数据的离散程度越小.
(2)标准差、方差的取值范围:[0,+∞).
标准差、方差为0时,样本各数据全相等,表明数据没有波动幅度,数据没有离散性.
标准差的意义
标准差刻画了数据的离散程度或波动幅度,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小.
1.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到如下列联表(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
常喝
不常喝
合计
肥胖
2
不肥胖
18
合计
30
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)现从常喝碳酸饮料且肥胖的学生中(2名女生),抽取2人参加电视节目,则正好抽到一男一女的概率是多少
P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
K
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:K2=
,其中n=a+b+c+d)
【答案】
(1)解:设常喝碳酸饮料肥胖的学生有x人,
.
常喝
不常喝
合计
肥胖
6
2
8
?不胖
4
18
22
合计
10
20
30
(2)解:由已知数据可求得:
因此有99.5%的把握认为肥胖与常喝碳酸饮料有关
(3)解:设常喝碳酸饮料的肥胖者男生为A、B、C、D,女生为E、F,则任取两人有
AB,AC,AD,AE,AF,BC,BD,BE,BF,CD,CE,CF,DE,DF,EF,共15种.
其中一男一女有AE,AF,BE,BF,CE,CF,DE,DF.共8种.
故抽出一男一女的概率是
【考点】独立性检验的应用,列举法计算基本事件数及事件发生的概率
【解析】(1)设常喝碳酸饮料肥胖的学生有x人,
.即可将上面的列联表补充完整;(2)根据列联表所给的数据,代入求观测值的公式,把观测值同临界值进行比较,得到有99.5%的把握说看营养说明与性别有关.(3)利用列举法,求出基本事件的个数,即可求出正好抽到一男一女的概率.
2.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名五年级学生进行了问卷调查,得到如下2×2列联表,平均每天喝500
以上为常喝,体重超过50
为肥胖.
?
不常喝
常喝
合计
肥胖
50
不肥胖
40
10
50
合计
A
B
100
现从这100名儿童中随机抽取1人,抽到不常喝碳酸饮料的学生的概率为
.
附:参考公式:
,其中
.
临界值表:
P(
)
0.05
0.025
0.010
0.005
0.001
3.841
5.024
6.635
7.879
10.828
(1)求2×2列联表中的数据
,
,A,B的值;
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
【答案】
(1)解:根据题意,不常喝碳酸饮料的学生为
,
∴
,
,
;
(2)解:有99.5%的把握认为肥胖与常喝碳酸饮料有关,理由如下:
由已知数据可求得:
,
因此有99.5%的把握认为肥胖与常喝碳酸饮料有关.
【考点】独立性检验的应用
【解析】(1)利用实际问题中的已知条件求出并填写出2×2列联表中的数据
,
,A,B的值。
(2)利用(1)中的2×2列联表结合独立性检验的方法,从而判断出有99.5%的把握认为肥胖与常喝碳酸饮料有关。
3.某公司有1000名员工,其中男性员工400名,采用分层抽样的方法随机抽取100名员工进行5G手机购买意向的调查,将计划在今年购买5G手机的员工称为“追光族",计划在明年及明年以后才购买5G手机的员工称为“观望者”,调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人.
附
,其中
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)完成下列
列联表,并判断是否有95%的把握认为该公司员工属于“追光族"与“性别"有关;
属于“追光族"
属于“观望者"
合计
女性员工
男性员工
合计
100
(2)已知被抽取的这100名员工中有10名是人事部的员工,这10名中有3名属于“追光族”.现从这10名中随机抽取3名,记被抽取的3名中属于“追光族”的人数为随机变量X,求
的分布列及数学期望.
【答案】
(1)解:由题意得,2×2列联表如下:
属于“追光族"
属于“观望者"
合计
女性员工
20
40
60
男性员工
20
20
40
合计
40
60
100
,故没有95%的把握认为该公司员工属于“追光族"与“性别"有关;
(2)解:由题意得,随机变量X的所有可能的取值为0,1,2,3,
;
;
;
.
所以
的分布列为
X
0
1
2
3
P
【考点】独立性检验,离散型随机变量及其分布列,离散型随机变量的期望与方差
【解析】(1)根据题意,列出列联表,计算K2
,
查表判断即可;(2)随机变量X的所有可能取值为0,1,2,3,分布求出对应概率,列出分布列,求期望即可.
4.近年来,我国肥胖人群的规模急速增长,肥胖人群有着很大的健康隐患.目前,国际上常用身体质量指数(英文为
,简称
)来衡量人体胖瘦程度以及是否健康,其计算公式是
中国成人的
数值标准为:
为偏瘦;
为正常;
为偏胖;
为肥胖.某地区随机调查了6000名35岁以上成人的身体健康状况,其中有1000名高血压患者,得到被调查者的频率分布直方图如图:
参考公式:
,其中
.
参考数据:
0.25
0.10
0.050
0.010
0.001
1.323
2.706
3.841
6.635
10.828
(1)求被调查者中肥胖人群的
平均值
;
(2)根据频率分布直方图,完成下面的2×2列联表,并判断能有多大(百分数)的把握认为35岁以上成人高血压与肥胖有关?
肥胖
不肥胖
总计
高血压
非高血压
总计
【答案】
(1)解:由图可知,1000名高血压患者中:
,
,
,
人数
5000名非高血压患者中:
,
,
,
人数
被调查者中肥胖人群的
平均值
.
(2)解:由(1)及频率分布直方图知,1000名高血压患者中有
人肥胖,5000名非高血压患者中有
人肥胖,所以可得下列列表:
肥胖
不肥胖
总计
高血压
350
650
1000
非高血压
1150
3850
5000
总计
1500
4500
6000
由列联表中数据得
的观测值为
,
所以能有
的把握认为35岁以上成人高血压与肥胖有关.
【考点】频率分布直方图,独立性检验
【解析】(1)利用频率分布直方图,填写分布表,利用频率分布直方图求解被调查者中肥胖人群的
平均值;
(2)求出
,
对照参考数据,判断有多大
(百分数)
的把握认为35岁以上成人高血压与肥胖有关。
5.某公司有1400名员工,其中男员工900名,用分层抽样的方法随机抽取28名员工进行5G手机购买意向调查,将计划在今年购买5G手机的员工称为“追光族”,计划在明年及明年以后购买5G手机的员工称为“观望者”,调查结果发现抽取的这28名员工中属于“追光族”的女员工有2人,男员工有10人.
附:
,其中
.
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)完成下面2×2列联表,并判断是否有95%的把握认为该公司员工属于“追光族”与“性别”有关;
属于“追光族”
属于“观望者”
合计
女员工
男员工
合计
28
(2)在抽取的属于“追光族”的员工中任选4人,记选出的4人中男员工有
人,女员工有
人,求随机变量
的分布列与数学期望.
【答案】
(1)解:由题意得:2×2列联表如下:
属于“追光族"
属于“观望者"
合计
女员工
2
8
10
男员工
10
8
18
合计
12
16
28
,
故没有95%的把握认为该公司员工属于“追光族”与“性别”有关;
(2)解:由(1)知在样本里属于“追光族"的员工有12人.其中男员工10人,女员工2人,
所以
可能的取值有
,
,
,
,
的分布列为:
0
2
4
的期望
.
【考点】独立性检验的应用,离散型随机变量及其分布列
【解析】(1)利用实际问题的已知条件填写
2×2列联表,
再利用
2×2列联表结合独立性检验的方法,判断出没有95%的把握认为该公司员工属于“追光族”与“性别”有关。
(2)利用分层抽样的方法推出属于“追光族"的员工有12人,其中男员工10人,女员工2人,
所以
可能的取值有
,
进而利用组合数公式结合古典概型求概率的方法,从而求出随机变量
的分别列,再利用随机变量
的分布列结合数学期望公式,进而求出随机变量
的数学期望
。
6.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对
名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝
以上为“常喝”,体重超过
为“肥胖”.
常喝
不常喝
合计
肥胖
2
不肥胖
18
合计
30
已知在全部
人中随机抽取
人,抽到肥胖的学生的概率为
.
附:
?
p(k2>k)
0.15
0.10
0.05
0.25
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)请将上面的列联表补充完整;
(2)是否有
的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
(3)已知常喝碳酸饮料且肥胖的学生中恰有2名女生,现从常喝碳酸饮料且肥胖的学生中随机抽取2人参加一个有关健康饮食的电视节目,求恰好抽到一名男生和一名女生的概率.
【答案】
(1)解:设全部30人中的肥胖学生共
名,则
,解得
.∴常喝碳酸饮料且肥胖的学生有6名.列联表如下:
常喝
不常喝
合计
肥胖
6
2
8
不肥胖
4
18
22
合计
10
20
30
(2)解:有;
理由:由已知数据可求得
,因此有99.5%的把握认为肥胖与常喝碳酸饮料有关.
(3)解:根据题意,可设常喝碳酸饮料的肥胖男生为
,女生为
,则任取两人,
可能的结果有
?共15种,其中一男一女有
,
共8种.故正好抽到一男一女的概率为
【考点】独立性检验,相关系数,列举法计算基本事件数及事件发生的概率
【解析】(1)由已知数据,即可将列联表补充完整;
(2)
由已知数据可得
,即可判断相关关系;
(3)由已知利用列举法,分别得
随机抽取2人和恰好抽到一名男生和一名女生的种数,即可求出概率.
7.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名五年级学生进行了问卷调查,得到如下2×2列联表,平均每天喝500ml以上为常喝,体重超过50kg为肥胖.
不常喝
常喝
合计
肥胖
x
y
50
不肥胖
40
10
50
合计
A
B
100
现从这100名儿童中随机抽取1人,抽到不常喝碳酸饮料的学生的概率为
(1)求2×2列联表中的数据x,y,A,B的值;
(2)根据列联表中的数据绘制肥胖率的条形统计图,并判断常喝碳酸饮料是否影响肥胖?
(3)是否有99.9%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
附:参考公式:K2=
,其中n=a+b+c+d.
临界值表:
P(K2≥k)
0.05
0.025
0.010
0.005
0.001
k
3.841
5.024
6.635
7.879
10.828
【答案】
(1)解:根据题意,不常喝碳酸饮料的学生为A=100×
=60,∴x=60﹣40=20,y=50﹣20=30,B=30+10=40
(2)解:根据列联表中的数据得常喝饮料的肥胖率为
=0.75,
不常喝饮料的肥胖率为
=0.33,
绘制肥胖率的条形统计图如图所示;
根据统计图判断常喝碳酸饮料会增加肥胖的可能
(3)解:由已知数据可求得:K2=
≈15.629>7.879,
因此有99.5%的把握认为肥胖与常喝碳酸饮料有关.
【考点】独立性检验
【解析】(1)根据题意,计算不常喝碳酸饮料的学生A,以及对应表中x、y和B的值;(2)根据列联表中的数据计算常喝饮料与不常喝饮料的肥胖率,绘图即可;根据统计图即可得出概率结论;(3)计算观测值K2
,
对照数表即可得出结论.
8.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名六年级学生进行了问卷调查得到如图联表.且平均每天喝500ml以上为常喝,体重超过50kg为肥胖.已知在全部100人中随机抽取1人,抽到肥胖的学生的概率为0.8.
常喝
不常喝
合计
肥胖
60
不肥胖
10
合计
100
(1)求肥胖学生的人数并将上面的列联表补充完整;
(2)是否有95%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
附:参考公式:x2=
P(x2≥x0)
0.05
0.025
0.010
0.005
0.001
x0
3.841
5.024
6.635
7.879
10.828
【答案】
(1)解:在全部100人中随机抽取1人,抽到肥胖的学生的概率为0.8,则肥胖的学生为80人;
常喝
不常喝
合计
肥胖
60
20
80
不胖
10
10
20
合计
70
30
100
(2)解:由已知数据可求得:K2=
≈4.76>3.841,
因此有95%的把握认为肥胖与常喝碳酸饮料有关
【考点】独立性检验的应用
【解析】(1)根据在全部100人中随机抽取1人,抽到肥胖的学生的概率为0.8,做出肥胖的学生人数,即可填上所有数字.(2)根据列联表所给的数据,代入求观测值的公式,把观测值同临界值进行比较,得到有95%的把握说看营养说明与性别有关.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
